单通道下基于盲源分离OFDMA抗干扰算法

沈　雷，胡桃桃，王彦波

(1.杭州电子科技大学通信工程学院，浙江 杭州 310018；2.国网浙江省电力公司信息通信分公司，浙江 杭州 310018)



单通道下基于盲源分离OFDMA抗干扰算法

沈雷1，胡桃桃1，王彦波2

(1.杭州电子科技大学通信工程学院，浙江 杭州 310018；2.国网浙江省电力公司信息通信分公司，浙江 杭州 310018)

利用OFDMA信号中IFFT矩阵的重复性，提出了单通道下基于子载波信息辅助盲源分离OFDMA抗干扰算法.算法将干扰信号建模成虚拟用户进行解码分离，在解码过程中并不需要去除CP部分,增加了信道能量，相比传统基于频域滤波并去除CP解码算法，具有更好的抗干扰性能.

正交频分多址接入；抗干扰；盲源分离

0　引　言

正交频分多址接入(Orthogonal Frequency Division Multiple Access，OFDMA)技术以频谱利用率高，数据传输速率快等优点广泛应用于各种通信网络.由于频谱拥挤和恶意干扰的存在，OFDMA通信系统往往受到各种干扰的影响，从而通信性能变差[1].单音干扰由于产生简单，干扰功率集中，对通信系统具有较好的干扰效果，受到了较多关注[2].目前的抗干扰技术主要有时域处理技术[3]、频域处理技术[4-5]以及子空间投影技术[6].

时域抗窄带干扰技术主要利用宽带信号和窄带信号相关性的不同，对窄带信号进行自适应预测并去除干扰.该算法抗干扰效果受算法的稳态性能，收敛性能，跟踪性能影响较大[3].频域滤波是利用OFDMA信号、窄带干扰信号以及白噪声不同频域表现特征并使用频域陷波算法滤除干扰.这种算法需要检测干扰频点，而且陷波处理会使有用信号频谱损失，使抗干扰效果变差.OFDMA频域抗干扰的另一种处理方法是利用单音干扰的频谱特性重构单音干扰并在时域进行抵消来完成抗干扰[5].这种方法的不足之处在于算法性能对参数估计的精确度极其敏感，实际信道中利用混合信号的频谱信息很难准确估计参数，使得干扰重构抵消方法性能降低.文献[6]提出了子空间投影滤波技术，利用自相关矩阵求解干扰子空间，将数据投影到干扰子空间并从接收数据中滤除.该算法避开了传统的时域，频域的繁琐分析和对模型参数估计的误差.基于子空间投影的滤波方法只能消除干扰信号与用户信号的二阶相关部分，且该算法在干信比较小的情况下，抗干扰性能急剧下降.

本文将单音干扰建模成OFDMA信号的虚拟用户，提出在单通道下将接收信号建模成基于子载波矩阵盲源分离的模型，利用独立分量分析法完成子载波矩阵解调，并对单音干扰和OFDMA用户信息进行分离，从而完成抗干扰.所提出的盲源分离抗干扰算法在分离过程中已完成了用户信息的解调，这种盲解调过程并不需要去除循环前缀(Cyclic Prefix，CP)部分，而传统的抗干扰算法在解调过程中都需去除CP.

1　单通道下OFDMA系统盲源分离抗干扰建模

单音干扰下，多径信道接收端接收到的OFDMA调制信号表示如下：

(1)

其中，bkn,p∈{±1}为第k个用户的第p个子载波的第n个数据信息.L表示OFDMA调制子载波总数，采用交织型分配给K个用户，每个用户占用P(P=L/Q)个子载波组成，那么第k个用户所包含的子载波集合为{qk,Q+qk,…,(P-1)Q+qk}，其中qk=1,2,…,Q.hkl,akl分别为第k个用户的第l条路径信号的幅度和延迟，用户的多径数均为Lc且多径延时符号数akl∈{0,1,…,Lc-1}.单音干扰j(m)=ρjej(ωjm+θj)，ρj是幅度，ωj是频率，θj是相位，n(m)是高斯白噪声.

在多径情况下接收端信号采样2(L+Lp)个点，组成向量表示如下：

qn=HFDBn+Jn+Nn，

(2)

其中，Nn是2(L+Lp)×1维的复高斯白噪声向量，其实部和虚部独立同分布，服从N(0,σ2).Bn是大小为3KP×1的OFDMA用户组成的信号向量，H是大小为2(L+Lp)×2(L+Lp+Lc-1)的多径信道矩阵，F是大小为2(L+Lp+Lc)×2KP的OFDMA的IFFT调制矩阵，D是由单位矩阵组成的改变信号组成结构的矩阵，其具体表示如下：

(3)

F=diag(F1,F2)2(L+Lp+Lc-1)×2KP

(4)

其中，F=diag(F1,F2)(L+Lp+Lc-1)×2KP，F1和F2分别代表延时T的不完整子载波矩阵和没有延时的不完整子载波矩阵：F1=[e11,…,ekp,…,eKP](L+Lp-T)×KP，F2=[e11′,…,ekp′,…,eKP′](L+Lp-T)×KP，ekp和ekp′分别是延时T的子载波向量和不完整的子载波向量：

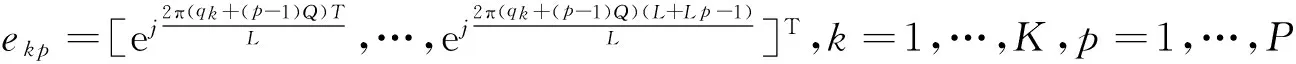
(5)

(6)

其中，H=diag(h,h)2(L+Lp)×2(L+Lp+Lc-1)，h表示多径卷积信道：

(7)

将式(3-7)代入式(2)可得：

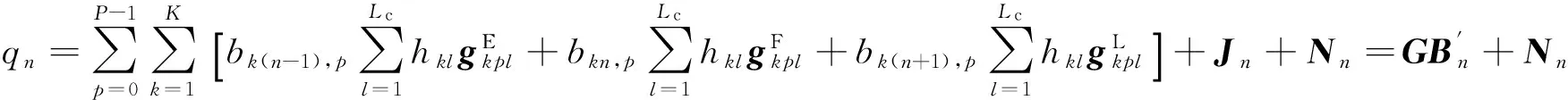
(8)

其中，G为混合矩阵，大小为2(L+Lp)×(3KP+2)，其具体表示如下：

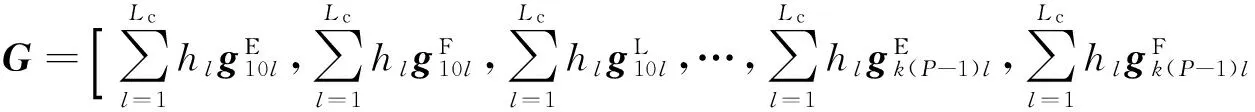
(9)

式(9)体现了该算法将OFDMA系统中的单音干扰建模成虚用户[7]，其虚拟子载波为ρjgjC和ρjgjS.G中包含5类不同状态的子载波，其中gkplE，gkplF，gkplL向量分别代表用户的延时T的不完整加长子载波向量，完整的加长子载波向量以及不完整的加长子载波向量，gjC和gjS代表干扰信号的子载波向量，其具体表示如下：

(10)

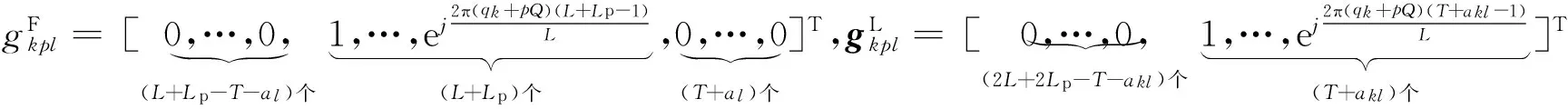
(11)

(12)

Bn′是由(3KP+2)个信源组成的向量，且各个信源之间都是统计独立的，其表示如下：

cos(ωj(L+Lp)n),sin(ωj(L+Lp)n)]T，

(13)

其中，bkn,p代表第k个用户的第p个子载波的第n个数据信息.由式(9-13)可知，混合矩阵G和独立信源矩阵Bn′均是由OFDMA用户信号和干扰信号两部分组成.其中混合矩阵包含了用户的子载波信息和干扰信号的频率信息，而信源矩阵则由OFDMA用户数据和干扰信号的(L+Lp)倍频率的正弦波组成.

2　基于子载波辅助的OFDMA系统盲源分离抗单音干扰算法

由以上的建模过程可知，盲源分离模型的混合矩阵G的列向量由OFDMA用户的子载波序列向量以及单音干扰特征序列向量构成，即混合矩阵列线性无关，可知混合矩阵G列满秩，此外由OFDMA用户信息和干扰信息组成的信源矩阵Bn′，信源之间具有统计独立性.

本文提出单音干扰下基于子载波序列辅助的独立分量分析OFDMA抗干扰算法，利用OFDMA信号的IFFT矩阵的重复性，将观测信号建模成超定盲源分离模型，并将OFDMA信号与干扰分离以完成抗干扰.

由于传统的独立分量分析(Independent Component Correlation Algorithm ，ICA)算法，存在不唯一的局部收敛点，使得最终的分离信号在顺序上存在不确定性.本文提出的基于用户子载波序列信息辅助的独立分量分析抗单音干扰算法，采用子载波序列信息来对基于峭度的目标函数进行优化，使得目标函数具有最优唯一解，即可得到特定OFDMA用户的信息序列，消除了分离信号顺序的不确定性，并完成抗干扰.

由式(2)可知，观测信号qn是2(L+Lp)×1维的复向量，组合其实部虚部表示如下：

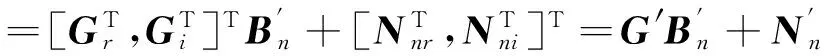
(14)

其中，qnr代表qn的实部，qni代表qn的虚部，G的实部Gr和虚部Gi构成新的混合矩阵G′，Nn的实部Nnr和虚部Nni构成新的噪声矩阵Nn′.为了消除观测信号中独立信源之间的相关性并降低信号维度，需对其进行预白化.首先根据qn′计算协方差矩阵Rq=E{qn′qn′H}，再进行奇异值分解Rq=UIUH.其中U=[Us,Un]，I=diag(Is,In)，这里Us=[U1,U2,…,U3KP+2]是大小为4(L+Lp)×(3KP+2)的信号子空间，Un=[U3KP+3,U4(L+Lp)]是4(L+Lp)×(4L+Lp-3KP-2)的噪声子空间，Is=diag(λ1,λ2,…,λ3KP+2)，In=diag(λ3KP+3,…,λ4(L+Lp))，O是元素均为零的矩阵，Ui(i=1,2,…,4(L+Lp))是Rq的特征向量，λi(i=1,2,…,4(L+Lp))是Rq的特征值.

令白化矩阵为Z=Is-1/2UsH，其大小为(3KP+2)×4(L+Lp)，白化后的数据为x，其大小为(3KP+2)×1，具体表示如下：

(15)

式中,令A=ZG′，其大小为3(KP+2)×3(KP+2)，是白化后的混合矩阵，白化使得信号维数由4(L+Lp)降为(3KP+2)，N″是白化后的高斯白噪声矩阵.最后对白化后的信号x进行独立分量分析，在此利用基于非高斯性极大化判据四阶统计量峭度的独立分量分析算法来实现盲源分离，用迭代算法得到合适的向量w，使得期望用户的性能函数J(w)输出最大：

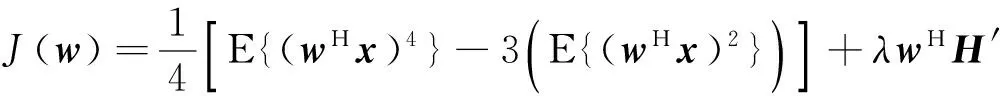
(16)

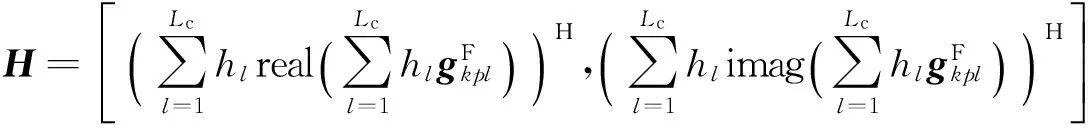
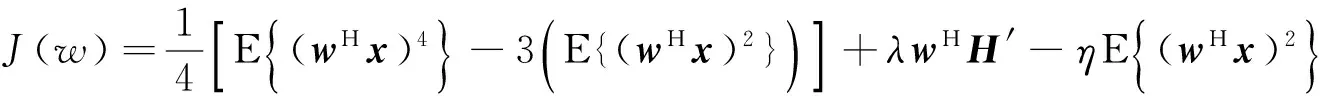
(17)

对式(17)求w的梯度，如下所示：

(18)

式中，η为常数，协方差矩阵M=E{xxH}.由式可以得到最优解为：

(19)

进而利用牛顿迭代法，可以得到w的更新公式：

(20)

通过式(19-20)，可以从OFDMA接收的混合信号中将期望用户信息分离出来，从而完成抗干扰.

3　基于独立分量分析OFDMA系统抗干扰算法性能分析

(21)

均方误差SMSE[8]定义式如下所示：

(22)

将其展开可得到[8]：

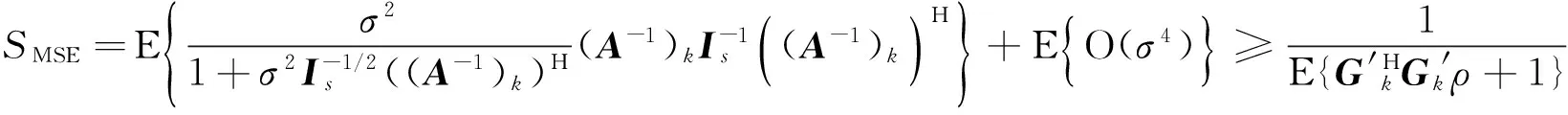
(23)

ρ为信噪比，由于衰落系数服从复标准正态分布，则有|hi|2～χ2(2),i=1,2,3,4，且每一条径的系数彼此独立，那么有：

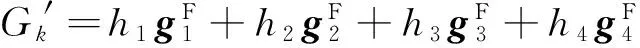
(24)

结合公式(24)对式(22)进一步推导可得：

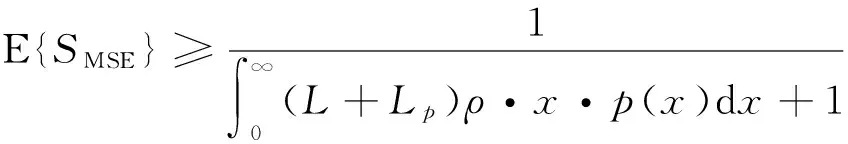
(25)

由式(25)知，均方误差理论下界与OFDMA数据块长度L，循环前缀长度Lp以及信噪比有关ρ.

4　实验结果与分析

为了比较，对目前广泛使用的基于频域滤波并用FFT解码的抗干扰算法和基于独立分量分析的OFDMA抗干扰算法在MATLAB平台下的环境下作蒙特卡洛仿真.本文仿真参数如下：信息采样频率为8 MHz，符号间隔为0.125 μs.子载波总数为L=32，用户数为4，每个用户所在的子载波分别为：3,7,16,23，频率分别为：f1=4.71 MHz，f2=10.99 MHz，f3=25.12 MHz，f4=36.11 MHz，循环前缀长度Lp=8，多径数Lc=4，多径幅度分别为h1，h2，h3，h4，以复高斯分布随机产生，在一个观测数据块内(信号样本数M=400)信道保持不变，多径延时分别为：[0,0.125 μs,0.25 μs,0.375 μs].单音干扰的频率ωj=5.18 MHz，信号的基带调制方式为BPSK调制.

图1和图2分别给出了用户1和用户4在各种抗干扰算法下的性能曲线.用户1和用户4所在的子载波为第3路和第23路.由于单音干扰频率，离第3路子载波的频率较近，离第23路子载波的频率较远，由文献[5]可知，对于子载波频率离干扰频率越近的用户数据，FFT解码时受单音干扰的影响越大.作FFT变换时，有限长数据引起频谱泄露，干扰信号的频谱也发生泄露.传统频域自适应滤波只能检测并消除能量较集中的频点上的大部分干扰，那些干扰能量较小的频点上小部分干扰难以完全消除，变换到时域后受干扰比较大的子载波用户信号受到的影响还是比较大，而受干扰比较小的子载波用户的受到的干扰更小.所以OFDMA频域抗单音干扰算法只对所处子载波上的信号受到干扰比较小的用户才有很好的效果.从图1和图2可知基于独立分量分析的OFDMA抗干扰算法性能比频域滤波抗干扰算法具有更好的性能，其次基于ICA抗干扰算法性能随CP变长而更好.这是由于所提算法不需去除CP，从而增加了接收信号能量.

图1　用户1抗干扰算法误码性能(信噪比)比较

图2　用户4的抗干扰算法误码性能(信噪比)比较

图3给出了在信噪比SNR=10 dB的同一条件下，用户1随干信比变化的基于独立分量分析的和基于频域滤波的OFDMA抗单音干扰算法性能比较.图3中，频域滤波抗干扰曲线反映了性能随着干信比增大变差.这是由于频谱泄露所产生的干扰频点上的干扰能量随干信比增大而增加，频域滤波算法只能对检测到的干扰较大的频点并进行陷波处理，而泄漏到其它频点上的分散的小部分干扰的总能量增加并且不能完全消除.基于独立分量分析的OFDMA的抗干扰算法把单音干扰建模成虚拟用户来进行分离，其抗干扰性能随着干信比的增大基本保持平稳，并且比频域滤波的抗干扰性能要好.由图3可知，基于盲源分离的OFDMA抗干扰算法比无单音干扰下传统的基于IFFT解码算法具有更好的性能.

图4给出了基于独立分量分析的OFDMA抗干扰算法的均方误差的仿真值与MSE理论推导下界的性能比较.信号观测样本数M=1 000，循环前缀Lp=8.从图中可见基于独立分量分析的OFDMA抗干扰算法的均方误差性能比频域抗干扰性能好，并且基本上与理论下界保持一致.

图3　用户1抗干扰算法误码性能(干信比)比较

图4　不同抗干扰算法的MSE性能比较

5　结束语

本文利用OFDMA信号中IFFT矩阵重复性，提出了基于用户子载波信息辅助独立分量分析的单通道OFDMA抗干扰算法.本文算法不需要干扰信号的任何先验知识，也不需要载波同步和去除循环前缀.仿真结果表明，相比于传统的基于频域滤波抗干扰算法，这种基于信号整体统计特性的抗干扰方法具有更好的性能.为今后的OFDMA系统的解码算法研究提供了理论和实践上的借鉴参考.

[1]ZHANGD,FANPY,CAOZG.InterferencecancellationforOFDMsystemsinpresenceofoverlappednarrowbandtransmissionsystem[J].ConsumerElectronics,IEEETransactionson, 2004, 50(1): 108-114.

[2]YANGCL,WANGM,WANGJX,etal.Single-Tonesignalingdesignforintercellinterferencemanagementwithapplicationstofemtocellnetworks[J].VehicularTechnology,IEEETransactionson, 2014, 63(3): 1242-1255.

[3]CHOIJW,CHONI.Suppressionofnarrow-bandinterferenceinDS-spreadspectrumsystemsusingadaptiveIIRnotchfilter[J].SignalProcessing, 2002, 82(12): 2003-2013.

[4]刘拥军,胡捍英.GPS频域抗干扰算法研究[J].信号处理,2009,25(11):1738-1741.

[5]应小凡,褚振勇,田红心,等.多载波扩频系统中单音干扰抵消的新方法[J].电波科学学报,2005,20(1):95-99.

[6]ZHOUF,WUR,XINGM,etal.Eigensubspace-basedfilteringwithapplicationinnarrow-bandinterferencesuppressionforSAR[J].IEEEGeoscienceandRemoteSensingLetters, 2007, 4(1): 75-79.

[7]沈雷,盛迪,孙闽红,等.单通道下基于盲源分离扩频通信抗干扰算法研究[J].电波科学学报,2014,29(5):922-927.

[8]SHENL,YAOYD,WANGH,etal.BlindDecodingBasedonIndependentComponentAnalysisforaMassiveMIMOUplinkSysteminMicro-CellRician/RayleighFadingChannels[J].VehicularTechnology,IEEETransactionson, 2015:1-9.

Anti-jamming Algorithm of OFDMA Communication Based on Blind Source Separation in Single Channel

SHEN Lei1, HU Taotao1, WANG Yanbo2

(1.SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China;2.ZhejiangElectricPowerCorporationInformationCommunicationsBranch,HangzhouZhejiang310018,China)

An anti-jamming method for OFDMA communication is proposed with single antenna. This method utilizes the repeatability of the IFFT matrix of the OFDMA signals and regards the interference signals as the virtual user in OFDMA. Thus, the interference can be cancelled by blind source separation. The proposed method also obtains more channel gain without removing the cyclic prefix(CP). Simulation results show that the proposed method outperforms conventional anti-jamming method based on frequency domain filtering.

orthogonal frequency division multiple access; anti-jamming; blind source separation

10.13954/j.cnki.hdu.2016.05.003

2016-04-01

国家自然科学基金资助项目(61401133)；中国博士后基金资助项目(20141473)

沈雷(1979-)，男，浙江杭州人，副教授，信号与信息处理.

TN911

A

1001-9146(2016)05-0011-06