对遗传算法的基本研究

梁望+李亮+王福顺

摘要：本文对遗传算法进行了基本的研究，从解码和译码、适应度函数以及遗传操作这三大部分来展开研究，给出了算法基本求解步骤以及流程图，最后给出了遗传算法的应用和推广。

关键词：遗传算法；基本求解步骤；遗传操作

中图分类号：TP301 文献识别码：A 文章编号：1001-828X（2016）022-000-01

一、遗传算法基本概念

遗传算法，是计算数学中用于解决最佳化的一种随机自适应全局优化搜索算法，属于进化计算。它模仿生物遗传学和自然选择机理，是对生物进化过程进行的一种数学仿真，基于随机自适应的全局搜索算法，自然界的“自然选择”和“优胜劣汰”即达尔文进化论，以及生物遗传学说这三大原理，为一些难以找到传统数学模型的难题指出了一个解决方法。

二、遗传算法三大部分

1.解码和译码

进化计算求解问题的第一步是对问题的可能解进行编码，目的是为了有效地执行遗传操作。这是一个从问题的解空间到编码空间的映射。编码是用简单的位串的形式来表示结构比较复杂的问题，译码是将问题结构而相反将位串形式编码表示变换为原问题结构的过程。在自然界生物进化中，把位串形式的解得编码表示叫染色体或基因型（基因表达）或者叫个体。原问题结构即一个染色体解码后所对应的解称为表现型。编码空间也称为基因型空间或搜索空间，解空间也叫做表现型空间。常见的编码方式有二进制编码、排列编码、实数向量编码以及结构式编码等。

2.适应度函数

类似于自然界中的自然生长过程，这一过程会受到很多因素的影响，最终决定该个体能否适应环境生存发展。在遗传算法中的适应度函数体现的就是染色体的适应能力，对该种群中每一个染色体，个体都能作用，进行度量的函数。在优化问题中，适应度函数就是目标函数，用来选出最优或是局部最优。当某一个染色体与问题的最优解染色体之间的差距比较小时，则表明该染色体适应度函数值与最优解之间的差值较小，相反，差距比较大时，则差值较大，有效的反映出两者之间的差距。在实际求解问题中选取适应度函数时有以下几点要求：1.因为适应度函数要比较排序进行选择，一般选取非负正值，连续的单一的2.具有合理性、一致性，较强的通用性3.是要求计算量较小，具体要根据实际问题本身而定。

3.遗传操作

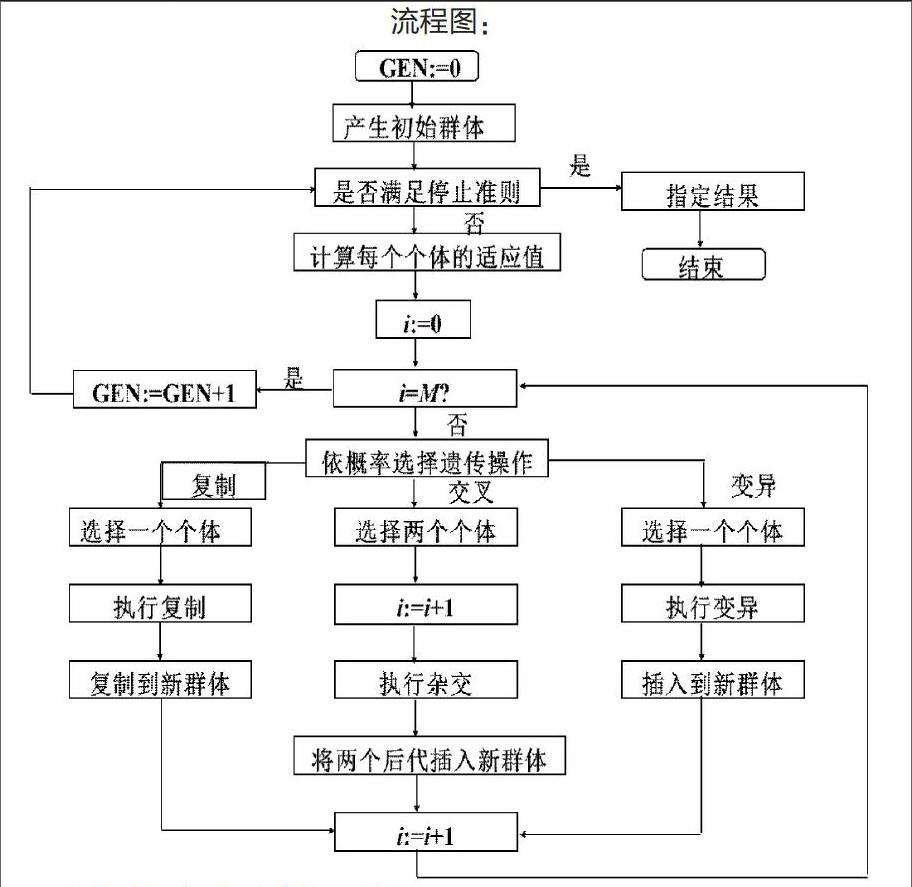
基本遗传算法的三个基本算子：选择，交叉，变异。

选择操作是根据个体的适应度函数值所度量的优劣成都决定它在下一代是被淘汰还是被遗传。从旧的种群中选择适应度高的染色体，放入匹配集（缓冲区），为以后染色体交换、变异，产生新的染色体做准备。一般采用适应度比例法（转轮法）来进行选择，按各染色体适应度函数值的大小比例来决定其被选择数目的多少。设某染色体被选的概率：，其中：Xi为种群中第i个染色体，f（xi）是第i个染色体的适应度值，Σf（xi）是种群中所有染色体适应度值之和。具体选择步骤如下：（1）计算各染色体适应度值（2）累计所有染色体适应度值（或选择概率），记录每个个体的适应度累加值（或概率累加值）（3）产生一个随机数 r，0< r

交叉操作：产生随机数，随机选择两个染色体，作为双亲染色体，根据实际情况选取一种合适的交叉方式例如：多点交叉、部分匹配交叉以及顺序交叉等来进行交叉变换，从而产生新的染色体，作为子辈的染色体。

变异操作：这一操作是在模拟生物进化中的基因突变环节，由于自然界或是外界环境发生改变，而影响了基因型的表达。在遗传操作常使用的染色体二进制编码中的变异操作很简单，若某一基因位为1则突变为成0，否则，由0变成1。生物进化中的突变可以丰富产生染色体的多样性，使同一物种有不同的表现型，不断进化发展。

三、遗传算法的基本求解步骤

（1）将种群初始化；

（2）利用适应度函数，计算种群中每个个体的适应度值；

（3）按照轮转法进行选择操作，选择出将要进入下一代的个体，这一环节中，适应度值大的选择的概率比较大，小的可能被淘汰，即优胜劣汰；

（4）按交叉概率Pc进行交叉操作，Pc的取值一般为0.4-0.99；

（5）按变异概率Pm进行突变操作，Pm的取值比较小，一般为0.001-0.1；

（6）若没有满足某种停止条件，则转第（2）步，否则进入下一步。停止条件与具体问题的应用有关，通常情况下设最大进化代数100-1000代。如果满足当前最优解的情况：很长时间最优解没有变化或是最优解达到一定的误差则找到最优解或满足解。

流程图：

四、遗传算法的应用及推广

遗传算法是一种新型的优化技术，它的经典应用领域就是对于一些非线性、多模型、多目标的函数优化处理；随着问题规模的增大，组合优化问题的搜索空间也急剧增大，可以利用遗传算法用来寻求满意解，它对于组合优化中的NP问题非常有效。另外遗传算法也在生产调度问题、自动控制、机器人学、图象处理、人工生命、遗传编码和自动程序设计等方面获得了广泛的运用和推广。

参考文献：

[1]赵云珍.遗传算法及其改进[D].昆明理工大学，2005.

[2]梁芳.遗传算法的改进及其应用[D].武汉理工大学，2008.

[3]王志美，陈传仁.遗传算法理论及其应用发展[J].内蒙古石油化工，2006，（09）：44-45.