基于小波变换的表面肌电信号低功耗压缩滤波算法*

毛东杰，张晓濛，蒋小文，黄　凯*

（1.浙江大学信息与电子工程学院，杭州310027；2.浙江大学电气工程学院，杭州310027）

基于小波变换的表面肌电信号低功耗压缩滤波算法*

毛东杰1，张晓濛2，蒋小文1，黄凯1*

（1.浙江大学信息与电子工程学院，杭州310027；2.浙江大学电气工程学院，杭州310027）

针对现有的表面肌电信号采集传输系统，提出三个算法分别对采样、传输、预处理这三个主要过程进行优化：在采集端降低采样功耗，在传输过程中通过低失真高倍率数据压缩减轻传输带宽负荷，从而降低传输功耗，在接收端通过信号预处理滤除工频干扰，同时对算法复杂度进行评估并提出参数的自适应策略。经仿真验证，本文提出的算法对低功耗表面肌电信号系统设计、优化具有较好的实用性。

表面肌电信号；低功耗；小波变换；压缩；工频滤除

EEACC：7220；7230doi：10.3969/j.issn.1004-1699.2016.05.004

表面肌电信号（SEMG）是人体肌肉收缩时伴随产生的生物电信号。未经处理的SEMG信号微弱，幅度在几十微伏到几毫伏，频率范围在6 Hz～500 Hz之间。其中占功率谱密度大部分的信号分布在20 Hz～150 Hz之间。

近年来，随着生物工程、医学和计算机技术的快速发展，具有人体交互功能的智能硬件与可穿戴体感设备成为开发热点，目前国内外有不少公司与研究机构从事SEMG信号研究。文献［1-6］设计了不同类型的SEMG信号采集传输系统，尽管能够便携地随身佩戴在人体表面进行高精度测量，但存在如下不足：①采集端持续高频率AD（数模转换器）采样与传输过程中大数据量原始数据传输易导致系统功耗过高、带宽负荷较大的问题，从而影响系统续航性能。②采集端用硬件滤波器对抗工频噪声极易造成有效信息的丢失。

针对以上问题，本文提出SEMG信号压缩滤波低功耗算法对以上系统方案进行优化，减少无用的静息电位数据采集，并对采得有效的动作电位数据压缩传输，进而降低数据采集与传输过程的功耗，减轻带宽负荷，并在接收端软件抑制工频干扰。

1　小波变换理论基础

小波变换继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的时间频率窗口，是进行信号时频分析和处理的理想工具［7］。

若ψ（t）∈L1（R）∩L2（R）ψ（t）dt=0则ψ（t）称为母小波。ψ（t）通过尺度伸缩和位移生成如下函数族：

其中a是尺度参量，b是位移参量。

设x（t）为信号函数，ψ（t）为母小波函数，则ψ（t）的连续小波变换定义表达式如下：

实际嵌入式系统中，主要为离散的数字信号，连续小波必须离散化［8］，故引入离散小波变换（DWT）的概念。令参数a=2-j，b=k2-j，其中j，k均为整数，则离散母小波为：

相对应的离散小波变换为：

由上述公式来看，离散小波变换可用卷积运算来执行，但考虑到实际系统卷积运算的计算量过大，为降低计算复杂度并且得到同样的小波变换结果，常常使用基于5/3可逆滤波器的小波变换提升算法［9］。实际SEMG信号多是由12 bit AD采样获得的2 byte整型数据，因此在滤波器选择的时候，考虑到重建信号质量和运算处理量，宜采用由5抽头低通滤波器和3抽头高通滤波器组成的5/3滤波器。下式为5/3可逆滤波器的小波变换提升算法数学表达式［10］，其中Sj-1，l为信号Sj，l的下一级小波变换系数，式中变换系数为2的幂次方整数，在乘除时可通过二进制数移位实现，通过简单乘加和迭代递推即可完成小波正变换与反变换，大大减少了计算复杂度。

5/3提升算法小波正变换：

5/3提升算法小波反变换：

2　系统与优化算法原理介绍

2.1SEMG采样传输系统简介

图1为现有的SEMG采样传输系统的整体框架，用测量电极将人体表面的肌电信号带通滤波放大后进行AD采样，然后用Wifi（无线局域网）或者蓝牙将数据传输到接收端，接收端收到数据后对信号进行分析。下面针对该系统中的AD采样、无线传输和接收分析部分分别进行优化。

图1　SEMG系统框架图

2.2低功耗采样检测算法

本算法核心思想是保证采集有效信号的完整性基础上，动态调整采样率来减少单位时间采样次数，让CPU更多时间处于休眠状态以降低数据采集过程中的功耗。

SEMG信号频率在0～500 Hz之间，根据奈奎斯特采样定理，一般用1 kHz的AD采样率对信号进行采样。从现有样本数据分析得，当前的采样方式中约有50%的时间对静息时刻无用的SEMG信号进行采样，而实际应用中仅在肢体产生动作电位时的SEMG信号对研究分析有作用，因此我们可通过检测有无动作电位来动态调整AD采样率：在静息时刻用低采样率来采集数据并检测动作电位是否来临；动作电位到来时切换成1 kHz的高采样率进行有效数据采集；当动作电位消失后，再切回低采样率等待动作电位再次来临。

如图2所示，从现有归一化SEMG信号数据分析得，静息时刻信号幅度波动比动作电位时刻小得多。静息时刻信号幅度的标准差约为0.023 5，而动作电位信号幅度的标准差约为0.198 3，两者相差约9倍，故可用标准差作为依据，用阈值法判断电位状态。在具体实现中主要考虑高低采样率之间的切换延迟时间与排除因个别异常信号而产生的误判，其中标准差阈值T的调整、低采样率的选择和求标准差的样本个数L选取较为关键。

图2　SEMG静息时刻与动作电位波形

实际系统可采用如图3的状态机对AD采样状态进行控制：当样本信号标准差（Std（data［L］））连续m次大于阈值（低到高采样计数变量L2 H_cnt＞m）则进入高采样状态，连续n次小于阈值（高到低采样计数变量H2L_cnt＞n）则进入低采样状态。

图3　采样控制状态机

2.3基于小波变换的自适应压缩算法

本算法参考图像处理领域的JP2000压缩算法并作适当修改，将SEMG信号阵列小波变换后的系数根据其特性进行自适应比特分配，得到低失真的最佳压缩方案后，用无线传输到接收端。

JPEG2000压缩算法能将图像压缩较高倍数且获得很小的失真度，其核心是将图像进行多级二维离散小波变换后的小波系数压缩编码。由于图像多数的能量与信息都存在于低频小波系数，其重要度远大于只反应图像细节信息的高频小波系数，因此可根据不同小波系数的重要程度分配不同的比特位数，如很多高频小波系数可直接量化为0而无需传输，此过程可产生较高压缩比。虽然JPEG2000压缩算法对图像压缩效果极佳，但要用到SEMG信号领域，首先要考虑如何将采集到的数据合理排布，增加各行各列之间的相关性，使其更具有图像特性，再者考虑的是在实际系统中如何用自适应的方法调整各部分小波系数的比特分配使压缩性能最佳。压缩重建过程如图4所示，总共N采样通道且每通道M个2 byte数据点，组成N×M的原始数据阵列，经过多级小波变换后得到N×M的2 byte小波系数，将小波系数量化压缩后发送到接收端，接收端用接收到的小波系数对SEMG信号进行重建。

图4　SEMG信号压缩重建过程

考虑到实际嵌入式系统实现时的计算复杂度，本系统用本文第2节提到的5/3小波变换提升算法进行二级二维小波变换，将小波系数的比特分配划分为16 bit、8 bit、0 bit（即2 bytes、1 byte、0 byte）3档，按低频系数比特分配优先于高频系数的原则将所有可能的分配方案进行枚举仿真，将压缩倍率与失真度之比作为衡量标准，用实际SEMG数据对自适应压缩算法进行仿真以得到最佳的压缩方案，考虑到实际应用，第4章将进行算法实用性讨论。

2.4基于小波变换的能量阈值滤波算法

经实际SEMG数据分析，采样过程中会不可避免地引入50 Hz、100 Hz的工频干扰，这些干扰不利于后续的信号分析。为避免原始采样数据有效信息的丢失，系统应尽量少用硬件滤波器［11］，而通过可调的软件方案对数据进行滤波。本文用基于小波变换的能量阈值滤波算法［12］在接收端对信号进行预处理，抑制工频干扰。

基于小波变换的滤波去噪过程如图5所示。小波变换的变尺度特性，对确定信号有一种“集中能力”［13］，例如50 Hz、100 Hz强工频干扰的表现为噪声信号能量集中于该频段附近小波变换域少数小波系数上，它们的取值必然大于该小波变换域内能量分散的大量信号的小波系数，因此我们可用软/硬阈值法将表现工频噪声的小波系数进行滤除，再将阈值处理后的小波系数重建为时域信号。本算法沿用本文第2节的5/3小波变换提升算法，且多级小波变换下一级的计算量比上一级少一半，故能用较低的计算复杂度来实现滤波过程，相比于传统数字陷波滤波器的高设计复杂度与模拟陷波滤波器易造成有用信号的丢失，本软件算法易于实现且成本较低，更适合嵌入式系统。小波去噪的关键在于信号序列的长度设定、小波分解尺度的选取与有效的阈值调整，以精确定位并剔除工频干扰的小波系数，第4章也会讨论算法实用性，供实际系统设计参考。

图5　SEMG信号去噪过程

3　算法验证与实验仿真

3.1低功耗采样检测算法性能仿真评估

根据2.2的低功耗算法，本系统设固定参数高采样率为1 kHz，低采样率为250 Hz，标准差阈值T+（Tstatic+Tmove）/2。设输入可调参数低转高采样阈值0≤m≤20，高转低采样阈值0≤n≤20，标准差样本数L=4，8，16，32，64，128。设输出结果误判率为α，切换延时比例为δ，采样功耗节省比例为ξ。结合输出结果，设性能衡量指标：η=（1-α）×ξ/δ，将所有参数可能情况用实际数据作枚举仿真，找出表达式η=（1-α）×=f（m，n，L）取最大值时的参数情况。本实验主要关注高低采样状态切换的延迟与采样状态误判率问题，切换延迟时间δ由m×L决定，而延迟过小可能使误判率升高。另外，高低采样状态切换的情况也不相同：由于低采样状态切换到高采样状态的延迟会导致过渡段动作电位数据欠采样，因此在保证误判率为0的基础上，降低m取值，使延时尽量小；而高采样状态转换到低采样状态只会采集一些多余静息电位时的数据，只需将n设高值，例如n=10，即可避免采样状态的误判。图6为最优化参数（m=2，n=10，L=16）情况下低功耗算法效果图，由仿真实验得，检测误判率为0，低采样转高采样的切换延迟时间占动作电位总时间的比例为2.69%，低采样状态时间为51.4%，采样功耗节省比例为38.5%。

图6　采样状态检测判别

3.2基于小波变换的自适应压缩算法性能仿真评估

图像处理领域的JPEG2000压缩算法中更关注图像低频小波系数的处理，如二级小波变换进一步将LL1小波系数变换为LL2、HL2、LH2、HH2后再编码压缩。而本实验压缩算法的数据对象为如图7所示的SEMG信号阵列，其每一行为单采样通道按时间排布的采样数据，故数据阵列的横向相关性较大；由于实际系统采用AD多通道同时采集数据，则数据阵列每一列为不同通道在同一时间点、同一身体部位采集所得的数据，也有一定纵向相关性，但比横向小的多。由于数据阵列横纵方向相关性差异较大，实验中对小波系数的处理方法要有所调整，若仅用LL1小波系数重建信号，会造成较大的失真。

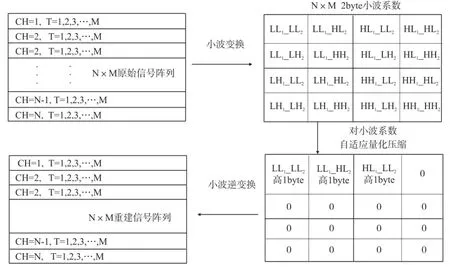
图7　最优化压缩方案

本算法将对LL1、HL1、LH1、HH14块一级小波变换区域再作二级小波变换，得到如图7所示LL1-LL2到HH1-HH2的16块二级小波变换系数，再对LL1， HL1，LH1，HH14块区域的系数各按0≤HH2≤LH2，HL2≤LL2≤2的约束条件分配比特数，将总共可能的204（160 000）种可能枚举仿真，输出压缩倍率CF与失真度PRD，其中Xr［i］［j］为重建信号，X［i］［j］为原始信号，然后以压缩性能为衡量指标，从所有比特分配方案中找出性能最佳的压缩方案，以模拟压缩算法参数自适应的调节过程。

如图7所示为最优化的压缩方案：将16块区域2 byte二级小波变换系数仅保留LL1-LL2、LL1-HL2、HL1-LL2的高1byte，其余全置零不传输，然后用这些压缩后的小波系数进行信号阵列重建，在实际应用中系统可自适应地调整压缩参数使其逼近最优方案。图8为某一通道动作电位时刻重建信号与原始信号的对比效果图，其中压缩倍率为32/3=10.7倍。根据24采样通道144个动作电位总计660万个数据点压缩重建误差统计，平均失真度PRD约为2.35%。

高压缩倍率低失真度的优势在于有效减轻传输带宽负荷，如在蓝牙等带宽受限的情况下可传输更多的数据，亦或在带宽要求不高的Wifi传输条件下降低传输功耗。此算法压缩过程把不重要的高频分量去除，而对20 Hz～150 Hz的SEMG有效信息几乎不影响，如图8所示，X_raw与X_rebuild分别为原信号与重建信号，第三幅图同时绘制原信号、重建信号与两者的Difference（绝对值差）。由图可知，重建信号与原始信号相似度非常高，则可说明压缩算法的有效性。

图8　压缩重建信号与原信号对比

3.3基于小波变换的能量阈值滤波算法

实际信号处理时，系统可自适应地调整序列长度并选择小波分解的层数，窄带定位至50 Hz、100 Hz附近小波系数区域，并对这两块小波系数区域分别进行基于α参数的非线性软阈值化［14］改造，得到新的小波系数后，将其重构为去噪后的信号。

图9、图10分别为实验仿真中序列长度64、6层小波分解条件下滤波前后时域与功率谱的对比图。从图9时域对比图来看，工频干扰造成的强底噪被明显抑制，静息时刻信号就代表工频噪声，两者对比去噪效果非常明显。图10为调用Matlab的周期法功率谱估计函数所得，图中50 Hz附近功率衰减约6 dB，100 Hz附近功率衰减约3 DB，其他频带功率无明显变化。

图9　去噪前后信号时域对比

图10　去噪前后信号功率谱对比

4　算法实用性讨论

4.1小波变换计算复杂度评估

本文所用的5/3提升算法小波变换可用硬件与软件两种方式实现：硬件方式可参考文献［10］的VLSI设计方案，长度为N的序列小波变换正变换与逆变换分别需要（N+6）与（N+5）个系统时钟周期；软件方式可参考文献［9］的算法公式，长度为N的序列共需要次加法与N次乘法，因二次幂乘法可用汇编移位运算指令来进行，实际再加上寄存器读写操作指令，小波正逆变换可用约3N条汇编指令完成。假设24通道肌电信号每64个采样点（即序列长度N=64）进行压缩传输，则1 kHz采样率下传输间隔为64 ms。根据理论推算，若采集端系统的25 MHz、32位CPU采用3.1节的最佳压缩方案，硬件与软件所需的小波变换压缩耗时分别为0.16 ms与1.44 ms，远小于64 ms的传输间隔；若接收端系统也为25 MHz的32位CPU，并采用3.3节仿真的滤波方案，硬件与软件耗时分别为0.57 ms与4.56 ms，仍远小于传输间隔。

无论使用软件或者硬件，基于小波变换的压缩与滤波算法均符合实时处理要求。硬件处理速度较快但定制计算模块成本较高，软件速度稍慢但其成本低、便于修改，具体选择还需衡量两者性价比。

4.2实际系统算法自适应策略

本文介绍的基于小波变换的压缩与滤波算法都需要参数自适应环节，才能使系统快速、自动地将算法参数调整到符合性能指标的状态。图11为算法参数自适应训练器的工作流程图，用户可选择参考先前的配置参数，以避免每次开机需重新配置参数造成的系统初始化缓慢；亦可选择重新配置参数，以若干有效信号数据作为训练样本，根据实时性能与要求指标的差值，选择步进大小，将参数由初始值快速逼近预期值，并存入非易失介质中，以便下次开机初始化时直接使用。在具体调整配置参数方面，压缩算法需根据不同小波系数优先分配更重要的比特位；而滤波算法根据实时性要求选定序列长度后，优先寻找不同层数小波变换最优化的软阈值，而后增加小波分解层数，以达到符合性能要求且复杂度最低的参数状态。

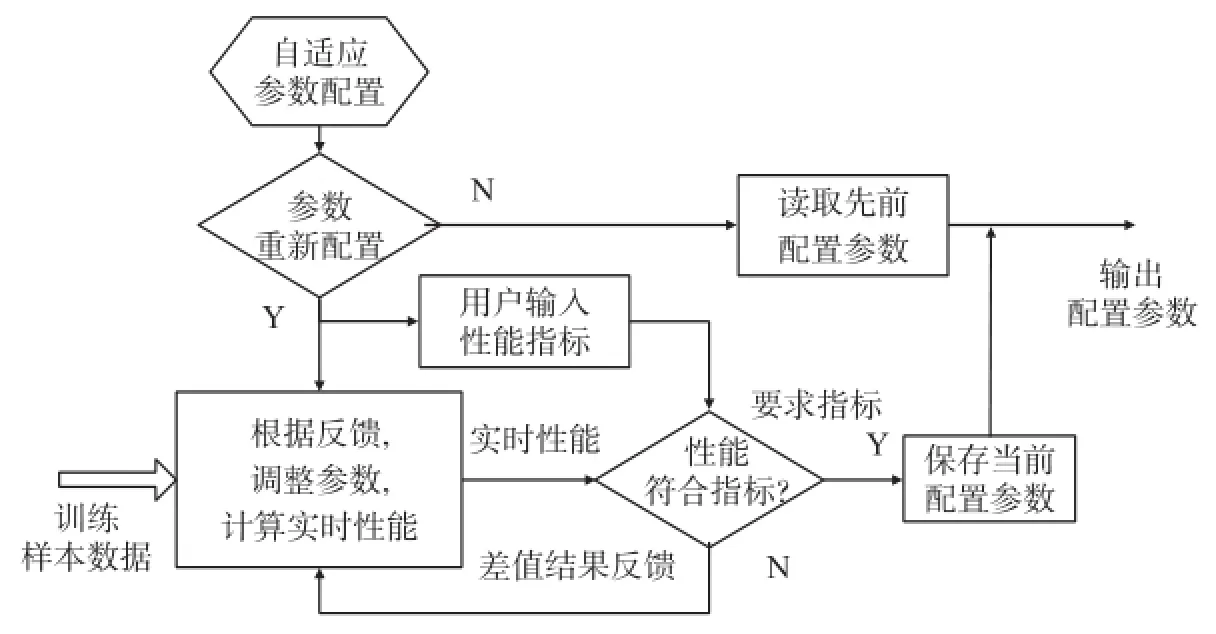
图11　参数自适应训练器

5　结论与展望

低功耗采样算法能降低38.5%的AD采样功耗，其代价为2.69%的动作电位数据欠采样，接收端可选择舍弃这段过渡数据或者内插补零，并不会影响动作电位数据整体的有效性。

基于小波变换的自适应压缩算法，其最优参数条件下可达到10.3倍压缩率，而仅产生2.35%的高频失真，其应用价值在于有效地降低传输带宽负荷与传输功耗，且保证数据的低失真。

基于小波变换的能量阈值滤波算法，能有效抑制50 Hz、100 Hz工频干扰，且对其他频带信息能完整保留，用低计算复杂度即可对接收端信号产生较好的滤波预处理效果。

以上三种算法可用于文献［1-6］的SEMG采集传输系统采样、传输、预处理过程的优化，并能自适应地调整算法参数，达到降低功耗、降低带宽负荷、抑制工频干扰的效果。

近年来，低功耗蓝牙（BLE）SOC芯片在智能体感硬件方面应用较为广泛，其优势在于低成本、单芯片、高集成度与低功耗，外设可用纽扣电池供电，小巧便携，续航持久，极适合可穿戴硬件领域，本文提出的三种算法对基于BLE的SEMG信号采集传输系统设计具有较高实用价值。

［1］Ahamed N U，Sundaraj K，Poo T S.Design and Development of an Automated，Portable and Handheld Tablet Personal Computer⁃Based Data Acquisition System for Monitoring Electromyography⁃Signals during Rehabilitation［J］.Proceedings of the Institution of Mechanical Engineers，2013，227（3）：262-274.

［2］胡也.基于WIFI的阵列式表面肌电信号采集与传输［D］.杭州：浙江大学信电学院，2014.

［3］李益栋.阵列式表面肌电信号的采集与噪声抑制［D］.杭州：浙江大学信电学院，2015.

［4］邱萍，朱旻，双丰.蓝牙无线表面肌电信号采集系统设计及应用［J］.仪表技术，2014，（2）：-10.

［5］左鹏飞，路知远，张永强，等.32通道无线表面肌电和加速度信号采集系统设计［J］.传感技术学报，2013，26（6）：790-795.

［6］万莎，侯文生，杨丹丹，等.基于LabVIEW的多通道sEMG信号检测系统设计［J］.电子测量与仪器学报，2009，23（11）：30-35.

［7］朱希安，曹林.小波分析及其在数字图像处理中的应用［M］.北京：电子工业出版社，2012：10-11.

［8］王大凯，彭进业.小波分析及其在信号处理中的应用［M］.北京：电子工业出版社，2005：13-18.

［9］小野定康.JPEG2000技术［M］.强增福译.北京：科学出版社，2004：109-134.

［10］凌朝东，刘蓉，钱江，等.基于5/3提升小波变换的心电信号压缩算法及VLSI实现［J］.信号处理，2010，26（6）：930-935.

［11］席旭刚，加玉涛，罗志增.基于独立成分分析的表面肌电信号工频去噪［J］.仪器仪表学报，2009，22（5）：676-679

［12］张雪，王海燕，李保军.临床心电信号工频干扰小波去噪方法对比分析［J］.计算机测量与控制，2010，18（4）：902-905.

［13］程正兴.小波分析与应用实例［M］.西安：西安交通大学出版社，2006：12-15.

［14］席旭刚，左静，张启忠，等.多通道表面肌电信号降噪与去混迭研究［J］.传感技术学报，2014（3）：293-298

毛东杰（1991-），男，浙江宁波人，硕士研究生，主要研究方向为微传感技术、物联网、嵌入式系统，3100102119@zju. edu.cn；

黄凯（1980-），男，江西广丰人，浙江大学副教授，主要研究方向为处理器及系统芯片设计，huangk@vlsi.zju.edu.cn。

Low Power Compression Filtering Algorithm for Surface Electromyographysignal Based on Wavelet Transform*

MAO Dongjie1，ZHANG Xiaomeng2，JIANG Xiaowen1，HUANG Kai1*
（1.College of information and electronic engineering，Zhejiang University，Hangzhou 310027，China；2.College of electrical engineering，Zhejiang University，Hangzhou 310027，China）

Based on the existing system of sampling and transmitting surface electromyography signal，three algo⁃rithms has been performed to respectively optimize the critical process of sampling，transmitting and preprocessing：reducing the power consumption when sampling，reducing the transmission power and bandwidth load by high-rate data compression with low distortionduring transmission，filtering the power frequency interference at the receiving end.Also the complexity of algorithmsis evaluated and the adaptive strategy of parameters is put forward.The simula⁃tion results show that the proposed algorithms have a good practical value for the design and optimization of low pow⁃er surface electromyography signal system.

surface electromyography signal；low power consumption；wavelet transform；compression；filtering the power frequency interference

TP212

A

1004-1699（2016）05-0647-07

项目来源：浙江省自然科学基金项目（LY14F020026）；中央高校基本科研业务费专项资金项目（2013QNA5008）

2015-11-04修改日期：2016-01-15