基于场协同理论的电子元件散热CFD数值模拟*

马芳芳，云和明,2,3，李永真

（1.山东建筑大学热能工程学院，济南 250101；2.可再生能源建筑利用技术省部共建教育部重点实验室，济南 250101；3.山东省可再生能源建筑应用技术重点实验室，济南 250101）



基于场协同理论的电子元件散热CFD数值模拟*

马芳芳1，云和明1,2,3，李永真1

（1.山东建筑大学热能工程学院，济南 250101；2.可再生能源建筑利用技术省部共建教育部重点实验室，济南 250101；3.山东省可再生能源建筑应用技术重点实验室，济南 250101）

针对电子元件的散热问题，以电子元件为研究对象，采用CFD技术对以空气为冷却流体的电子元件的6种散热方案进行了数值模拟。采用流体固体共轭传热技术，获得电子元件散热小空间的温度场及速度场。基于场协同原理对其温度场和速度场的协同效果进行分析和比较，获得电子元件散热的优化方案，为进一步提高电子元件的散热效果及热设计水平提供理论依据。

CFD；数值模拟；场协同原理；共轭传热

1　引言

随着电子产品的快速发展，电子元件的散热设计在整个产品设计中占有越来越重要的地位。对于包括CPU在内的电子设备，现在的失效问题有55%是由于过热而引起的［3］,因此电子元器件的散热效果得到越来越多的重视。如何提高电子元件的散热效果，成为了电子元件发展所必须克服的问题。根据经典的强化传热理论，可以通过增加流量来增大雷诺数或者加肋以增加传热面积以及设置粗糙表面以提高湍流度等方法来强化对流换热。但是这些措施往往伴随着流动阻力的增加，在实际应用上受到一定的限制。根据过增元等［4］提出的场协同理论，可以通过调节流场，增大速度分布和温度分布的均匀性以及减小速度矢量U和温度梯度矢量▽T之间的夹角来实现强化传热。本文基于场协同原理，采用CFD的流固共轭传热技术对电子元件的6种散热方案进行了数值模拟，模拟了以空气为冷却流体的电子元件散热小空间的温度场和速度场，并且依据场协同原理对其温度场和速度场的协同效果进行分析，获得电子元件散热的优化方案。

2　几何模型及控制方程

2.1几何模型

在数值计算中，选取6种散热方案并对不同的散热方案进行数值模拟。如图1所示，针对所有方案小空间内部布置着两个矩形电子元件，两个电子元件间隔1 cm，电子元件距离左右壁面的横向距离均为1.5 cm，各壁面绝热，速度无滑移。电子元件的封装材质为陶瓷，其物理特性参数为：密度500 kg/m3，比热0.84kJ/kg·k，导热系数0.21 W/m·k。每个电子元件的几何尺寸为1 cm×1.5 cm，且每个电子元件的发热功率为30 W（相当于热生成率为2×105W/m3）。

图16　种电子元件散热方案

如图1所示：方案一为强迫送风冷却，模型的左下角设为送风口，右下角设为出风口，进、出口尺寸均为0.5 cm；方案二为强迫送风冷却，模型的左下角设为送风口，右上角设为出风口，进、出口尺寸均为0.5 cm；方案三为强迫送风冷却，在模型上方设一个送风口，左右下角各设一个出风口，进、出口尺寸均为0.5 cm；方案四为强迫送风冷却，物理模型在方案三的基础上，将进、出口的尺寸扩大2倍即1 cm；方案五为空气射流冷却，送风口设在电子元件上方，在每个电子元件的两侧设立出风口，进、出口尺寸均为1 cm；方案六为空气射流冷却，在方案五的基础上，将两个送风口之间也设为送风口，即送风口尺寸为3 cm，出口尺寸为1 cm。在数值模拟中，均将送风口设为速度入口，出风口设为压力出口，并且所有方案的送风速度和空气的初始温度均分别为5 m/s和293 K。

2.2控制方程

以小空间整个流动区域中的传热流体为研究对象，建立数学模型。小空间内流体流动与传热的控制方程［1］为：

连续性方程：

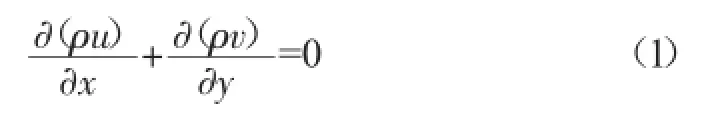
动量方程：

能量方程：

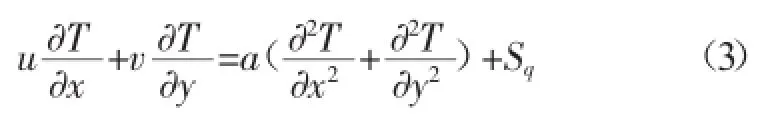
式中：u为流体的x方向速度分量，单位m/s；v为流体的y方向速度分量，单位m/s；p为流体的压力，单位Pa；T为流体的温度，单位K；β为流体的热膨胀系数，单位1/K；g为流体的重力加速度，单位m2/s；η为流体的粘性系数，单位Pa·s；a为流体的热扩散系数，单位m2/s；ρ为流体的密度，单位kg/m3；ρ0为流体的参考工作密度，单位kg/m3；T0为参考工作温度，单位K；Sq为流体的内热源项，单位K/s；x为x方向的矢量，单位m；y为y方向的矢量，单位m。

3　求解方法

采用CFD建立物理模型并划分网格，计算过程中采用有限容积法离散方程，同时求解流体的连续性方程、动量方程和能量方程。选取标准k-ε紊流模型，采用二阶迎风差分格式进行离散，控制方程的求解利用SIMPLEC算法。进口边界条件给定空气的进口平均流速、进口温度、k、ε等值；出口边界条件设定相对压力为零；电子元件给定等热生成率，其他壁面绝热。当能量方程中收敛残差小于10-6时，整个计算过程被认为收敛。并且计算做了如下基本假设：（1）空气的物性参数为常数；（2）流体在壁面上无滑移；（3）流体的流动是定常的；（4）电子元件给定等热生成率条件；（5）在重力方向上考虑浮升力的影响，满足boussinesq假设。

4　计算结果及比较

4.1速度场与温度场的分析

图2为方案一的温度场和速度场，从图中可看出空气从左下角进入后受到左边电子元件的阻挡和热浮升力的作用，而使得空间左上角部分产生逆时针的涡流。空气沿着电子元件从左到右流动，产生对空气的驱动作用，使两个电子元件的右侧均产生涡流，这有助于降低电子元件的温度。方案一的最高温度为电子元件部分的温度，达334 K（61℃），空气的最高温度为316 K（43℃），电子元件之间空气的温度从293 K（20℃）到316 K（43℃）之间变化。

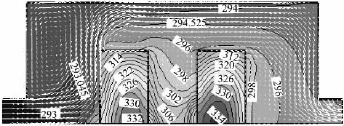
图2方案一的温度图和速度矢量图（单位/K）

图3为方案二的温度场和速度场，从图中可看出空气从左下角进入后受到左边电子元件的阻挡和热浮升力的作用，而使得空间左上角部分产生逆时针的涡流。空气沿着电子元件从左到右流动，产生对空气的驱动作用，使两个电子元件的右侧均产生涡流，这有助于降低电子元件的温度。方案二的最高温度为电子元件部分的温度，达334 K（61℃），空气的最高温度为316 K（43℃），电子元件之间空气的温度从293 K（20℃）到316 K（43℃）之间变化。

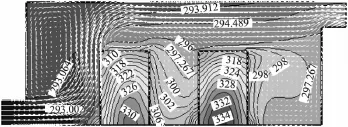
图3　方案二的温度和速度矢量图（单位/K）

图4为方案三的温度场和速度场，从图中可看出空气从上边两电子元件之间进入，空气从中间向两侧流动，从小空间的左、右下角分别流出。因受到电子元件的阻挡和热浮升力的作用，使得两侧即电子元件与壁面之间分别产生顺、逆时针的两个涡流。空气在电子元件上方流动，从而对电子元件间的空气产生驱动作用，使两个电子元件之间产生涡流，这有助于降低电子元件的温度。方案三的最高温度为电子元件部分的温度，达329K（56℃），空气的最高温度为320K（47℃），电子元件之间空气的温度从293K（20℃）到320K（47℃）之间变化。

图5为方案四的温度场和速度场，从图中可看出空气从上边两电子元件之间进入，空气从中间向两侧流动，从小空间的左、右下角分别流出。因受到电子元件的阻挡和热浮升力的作用，从而使得两侧即电子元件与壁面之间分别产生顺、逆时针的两个涡流。空气在电子元件上方流动，从而对电子元件间的空气产生驱动作用，使两个电子元件之间产生涡流，这有助于降低电子元件的温度。方案四的最高温度为电子元件部分的温度，达326 K（53℃），空气的最高温度为308 K（35℃），电子元件之间空气的温度从293 K（20℃）到308 K（35℃）之间变化。

图4　方案三的温度和速度矢量图（单位/K）

图5　方案四的温度和速度矢量图（单位/K）

图6为方案五的温度场和速度场，从图中可看出空气从上边进入直接对中间的电子元件进行冷却，空气沿对应电子元件向两侧流动，从小空间的左、右下角以及两个电子元件之间流出。因受到电子元件的阻挡和热浮升力的作用，从而使得两侧即电子元件与壁面之间分别产生顺、逆时针的两个涡流，这有助于降低电子元件的温度。方案五的最高温度为电子元件部分的温度，达317 K（44℃），空气的最高温度为295 K（22℃），电子元件之间空气的温度从293 K（20℃）到295 K（22℃）之间变化。

图7为方案六的温度场和速度场，从图中可看出空气从上边进入直接对中间的电子元件进行冷却，空气向两侧流动，从小空间的左、右下角以及两个电子元件之间流出。因受到电子元件的阻挡和热浮升力的作用，从而使得两侧即电子元件与壁面之间分别产生顺、逆时针的两个涡流，这有助于降低电子元件的温度。方案六的最高温度为电子元件部分的温度，达315K（42℃），空气的最高温度为295K（22℃），电子元件之间空气的温度从293K（20℃）到295K（22℃）之间变化。

图6　方案五的温度和速度矢量图（单位/K）

图7　方案六的温度和速度矢量图（单位/K）

4.2温度场和速度场的协同分析

湍流的二维能量协同方程如下［6］：

式中：Nut、Ret、Prt分别为湍流的努塞尔数、雷诺数和普朗特数；▽T为无量纲温度梯度。

无因次速度与无因次温度梯度的点积可表达为：

若矢量U与矢量T之间的夹角越小，则点积Ug▽T越大，层流努塞尔数Nu越大，流体与壁面间的对流换热也就越强。从而可推出湍流协同角表达式为：

当U恒定时，且T一定，β角越小，点积Ug▽T越大，努塞尔数Nu越大,流体与壁面间的换热越强。

基于场协同原理可得出速度与温度梯度的协同程度即协同角。协同角云图及等值线图如图8所示。

根据场协同原理以及协同角等值线图，如图8所示，方案一主流区的温度等值线和速度矢量几乎平行，此处协同角近似为80°，温度场与速度场的协同程度比较差。小空间左上角的涡流因速度同温度等值线近似平行，此处平均协同角大于80°，说明此涡流对于降低电子元件的温度基本不起作用。两个电子元件之间的涡流作用相互抵消，对降低电子元件的温度不起作用。右侧电子元件右侧的涡流与温度等值线夹角很小，即此处平均协同角近似90°，故温度场与速度场的协同程度很差，从而导致电子元件的温度较高。方案二与方案一的小空间内速度与温度梯度的协同程度类似，唯一不同在于方案二右侧电子元件与壁面之间充分形成涡流，致使此处的平均协同角小于85°，故而相对于方案一有效提高了换热效果。方案三在电子元件上方的协同角为80°，协同效果较差。电子元件之间中心处协同角最高至170°，故此处涡流对散热没有作用。电子元件与左、右两侧壁面之间的平均协同角大于80°，故速度场与温度场的协同程度较差。方案四与方案三的模型相似，小空间内电子元件上方的协同角近似80°，协同效果较差，电子元件之间中心处协同角最高至170°，故此处涡流对散热没有作用，电子元件与左、右两侧壁面之间的平均协同角大于80°，协同效果较差。方案五在电子元件上方和电子元件之间的协同角近似为50°，协同效果较好。小空间左、右上角的涡流处的平均协同角大于80°，此处速度场与温度场协同较差。电子元件与左、右两侧壁面之间的协同角近似80°，相对于方案四速度场与温度场的协同程度有所好转。方案六在电子元件上方和电子元件之间的协同角近似为50°，协同效果较好。小空间左、右上角涡流处的平均协同角近似为80°，此处速度场与温度场协同较差。电子元件与左、右两侧壁面之间的协同角近似80°，故方案六与方案五的小空间内速度与温度梯度的协同程度相类似。

为了反映电子元件的散热效果，通过定量分析流体速度场和温度场的协同程度来解决。根据场协同原理中湍流的二维能量协同方程，引入湍流平均协同角的计算，计算结果见表1。

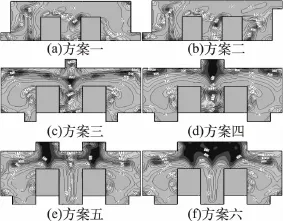
图8　协同角云图及等值线图

表1　6种电子元件散热方案的平均协同角

根据以上模拟结果以及流体速度场和温度场协同程度的定量分析，可以得出以下各方案之间的比较图，见图9、图10。

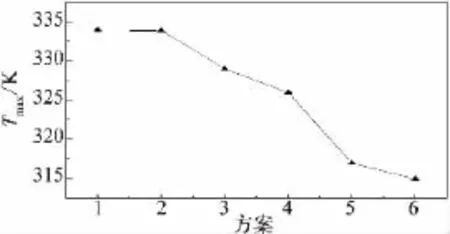
图9　各方案电子元件最高温度比较图

图10　各方案电子元件平均协同角比较图

电子元件的冷却效果与电子元件的最高温度密切相关，经过空气冷却，电子元件的最高温度越低，说明该方案电子元件的冷却效果越好。并且根据湍流的二维能量协同方程可知，各个方案的温度场和速度场的协同程度可综合反映电子元件冷却效果的优劣，即协同角越小，电子元件冷却效果越好。

如图9和图10所示，并根据比较可知：方案一至方案六顺序执行过程中电子元件的最高温度和平均协同角均呈逐渐降低的趋势，可知方案一至方案六顺序执行过程中空气的温度场和速度场协同程度越来越好，电子元件的冷却效果也顺次越来越好，另外各方案电子元件的最高温度依次逐渐降低，也从另一方面证明电子元件的冷却效果依次逐渐优化。通过对各种电子元件的散热方案进行CFD模拟，获得电子元件的最高温度和周围冷却空气的平均协同角，可有效实现电子元件散热方案的优化，为进一步提高电子元件的散热效果及热设计水平提供理论依据。

5　结论

计算结果表明，电子元件的冷却效果主要取决于冷却流体速度场和其温度场的协同程度，流体温度场和速度场协同程度越好，电子元件冷却效果相应越好。对电子元件进行基于场协同的热分析，可对电子元件的散热方案进行优化。通过利用CFD软件对二维小空间模型内的电子元件的冷却效果进行数值模拟，发现流体的温度场和速度场协同程度直接影响电子元件的冷却效果。基于场协同原理进一步获得电子元件散热方案的平均协同角，并以此平均协同角和电子元件的最高温度为评价指标获得电子元件散热的优化方案。本研究表明，利用CFD软件对电子元件进行基于场协同原理的热设计和热分析，可有效实现电子元件冷却方案的优化，为进一步探讨微电子器件的散热机理奠定了基础。

［1］陶文铨.数值传热学 ［M］.西安：西安交通大学出版社，1998.

［2］云和明，程林，陈宝明，等.电子元件散热的优化分析［J］.工程热物理学报，2006，27（3）：496-498.

［3］李楠,张东方,陈东哲.电子元件散热的数值模拟［J］.能源与节能,2012（5）：79-81.

［4］过增元.对流换热的物理机制及其控制：速度场与热流场的协同［J］.科学通报,2000,45（19）：2118-2122.

［5］云和明,李真,陈宝明.微小空间电子器件散热研究［J］.山东建筑大学学报,2004,19（1）：54-58.

［6］刘伟,刘志春,马雷.多场协同原理在管内对流强化传热性能评价中的应用［J］.科学通报,2012（10）：867-874.

［7］郭磊.电子器件散热及冷却的发展现状研究［J］.低温与超导,2014,42（2）：62-66.

［8］冷学礼,张冠敏,田茂诚,等.场协同原理在对流换热中的应用方法［J］.热能动力工程,2009,24（3）：352-354.

［9］夏翔鸣,赵力伟,徐宏,等.基于场协同理论的强化传热综合性能评价因子［J］.热能动力工程,2011,26（2）：197-201.

［10］周俊杰,陶文铨,王定标.场协同原理评价指标的定性分析和定量探讨 ［J］.郑州大学学报：工学版,2006,27（2）：45-47.

CFD Numerical Simulation of Electronic Equipment Cooling in the Perspective of Field Synergy Principle

MA Fangfang1,YUN Heming1，2，3,LI Yongzhen1
（1.School of Thermal Energy Engineering，Shandong Jianzhu University，Jinan 250101，China；2.Key Laboratory of Renewable Energy Utilization Technologies in Building，Ministry of Education，Jinan 250101，China；3.Shandong Key Laboratory of Renewable Energy Application Technology，Jinan 250101，China）

The paper simulates six cooling schemes for electronic components using CFD technology with air as cooling fluid and obtains the temperature and velocity fields in small space using fluid-solid conjugate heat transfer technology.After analyzing the synergy effect of the temperature and velocity fields using the field synergy principle,the optimized scheme is obtained,which improves the electronic components cooling performance and provides proofs for further studies.

CFD（computational fluid dynamics）；numerical simulation；field synergy principle；conjugate heat transfer

TN305.94

A

1681-1070（2016）09-0001-05

马芳芳（1990—），女，山东德州人，硕士研究生，研究方向为传热传质及应用；

2016-6-2

山东省自然基金（ZR2010EM06），住房和城市建设部项目（138），太阳能蓄能水箱蓄热、供热的开发研究。

云和明（1976—），男，山东滨州人，副教授，博士，主要研究方向为传热传质及应用。