有限导流压裂水平气井拟稳态产能计算及优化

王军磊，贾爱林，位云生，赵文琪

（中国石油勘探开发研究院，北京100083）

有限导流压裂水平气井拟稳态产能计算及优化

王军磊，贾爱林，位云生，赵文琪

（中国石油勘探开发研究院，北京100083）

在拟稳态流动阶段，边界封闭效应会对气井产能计算及优化产生很大影响。以单条人工裂缝为研究单元，在推导有限导流因子基础上，利用积分变换、渐近分析等方法获得单裂缝拟稳态压力基本解，基于势叠加原理、物质平衡方程建立矩形地层有限导流压裂水平井产能计算模型并迭代求解，同时回归产能关于压裂参数的导数极大值获得最优参数的函数关系线。结果表明：气井产能受裂缝条数、长度、间距、导流能力、相对位置及气藏几何形状等因素影响，增大裂缝与地层接触面积、减小缝间干扰、降低边界封闭效应、平衡裂缝与地层流入流出关系能有效提高气井产能；当裂缝系统均分气藏泄流面积时裂缝布局最优，而对应的裂缝最优导流能力关系线则随气藏矩形长宽比、裂缝条数的变化而变化；在最优参数作用下气井能较为显著地达到较高的产能水平，实际使用时应选取最优参数线附近区域作为优化压裂参数的参考范围。

水平井；有限导流；拟稳态；无量纲产能系数；参数优化

对于渗透率小、自然产能低的非常规气藏，利用水平井开发技术辅以水力压裂增产措施能有效增大泄流面积、减小渗流阻力、增加储量动用程度、提高气井产能。众多理论和实践表明，分段压裂水平井渗流机制复杂、受控因素多，气井产能受水平压裂段长度、裂缝条数、导流能力和裂缝长度等影响显著［1-2］，对其进行参数优化会引起复杂的非线性优化问题［3-4］。寻求简洁合理的产能计算和参数优化方法已成为提高压裂水平井开采效率的技术关键。近年来关于压裂水平井产能的计算主要集中在不稳态产能［5-7］和稳态产能［8-10］两方面，而实际气藏在生产晚期受到井间干扰和断层封闭的影响，通常进入拟稳态流动阶段。在边界封闭效应影响下，气井拟稳态产能公式有别于稳态产能公式［11-12］，影响产能的压裂参数较多且不独立，传统参数优化方法如枚举法、正交试验［13-14］等存在着最优解空间难以全部覆盖、方案数量过大的矛盾，而遗传算法［15-16］等智能技术难以解决由于裂缝条数增加而引起的搜索空间急剧增大的问题。笔者在建立分段压裂水平井拟稳态产能计算模型的基础上，研究压裂水平井的渗流本质，通过平衡裂缝与地层接触面积、地层边界封闭影响、裂缝间相互干扰、裂缝与地层流入流出动态4种渗流关系优化气井产能，并借助产能关于压裂参数的导数极大值获得最优参数的函数关系，利用积分平均方法确定压裂参数的优化参考值。

1 气井拟稳态产能计算

对于压裂水平井，人工裂缝是气体流动的主要通道，首先以单条裂缝作为基本研究单元，通过势叠加原理建立分段压裂水平井产能计算模型。

1.1 有限导流裂缝拟稳态压力模型

引入气体拟压力m、拟时间ta函数能够将气体渗流等效为液体渗流，

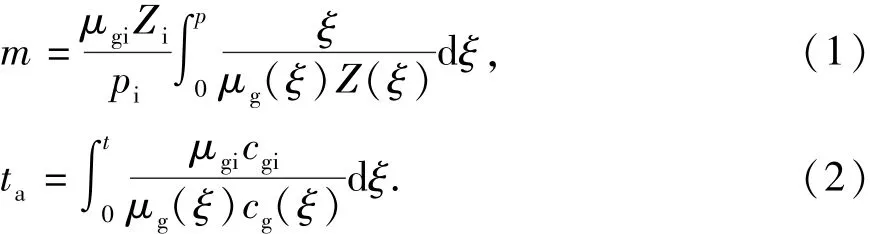
式中，μg为气体黏度，mPa.s；cg为气体压缩系数，MPa-1；Z为气体偏差因子；t为时间，h；p为压力，MPa。

假设垂直裂缝完全穿透地层，平面上平行于短轴边界xe（相当于1/2排距），长轴边界为ye（相当于水平井段长），裂缝流量为qfsc，位于（xw，yw）的长度为dxw微元对应流量为qfscdxw/（2xf），相应微元在地层中引起的无量纲拟压力控制方程为

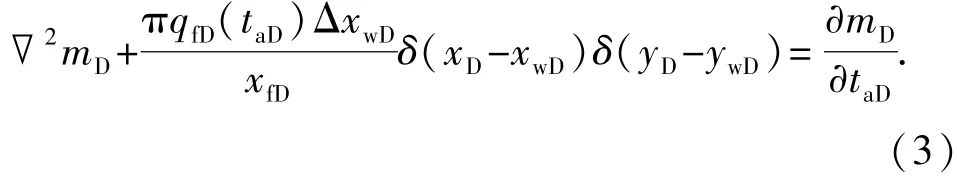
其中，气藏带有xeDyeD的矩形封闭外边界，初始时刻压力分布均匀：

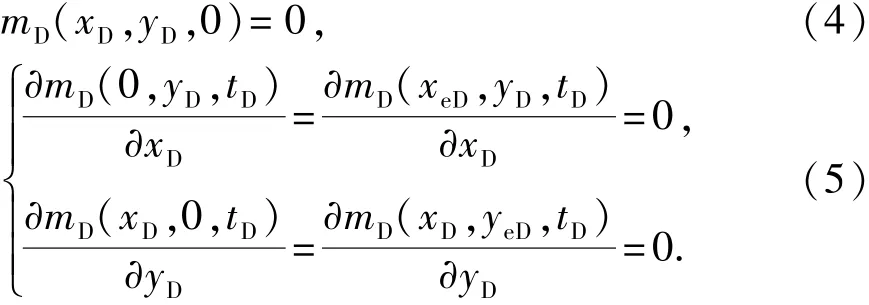
SI单位制下的无量纲量定义为

式中，km为基质渗透率，10-3μm2；kf为裂缝渗透率，10-3μm2；wf为裂缝宽度，m；xf为裂缝半长，m；h为气藏厚度，m；ye为气藏长轴，m；xe为气藏短轴，m；Lref为参考长度，m；qfsc为0℃、1 MPa下裂缝产量，m3/d；qref为参考产量，m3/d；CfD为无量纲裂缝导流能力。

利用Laplace变换、Fourier有限余弦积分变换及反变换处理式（3）～（5），得到Laplace空间下的微元压力基本解［17-18］，

其中

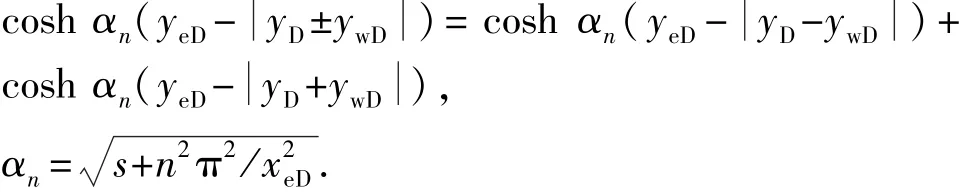
利用线性叠加原理，沿裂缝面积分获得均匀流量裂缝压力解为

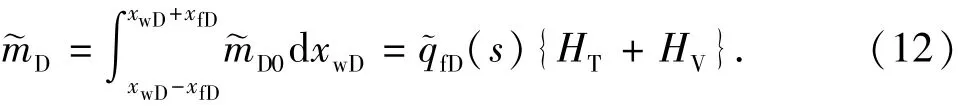
其中

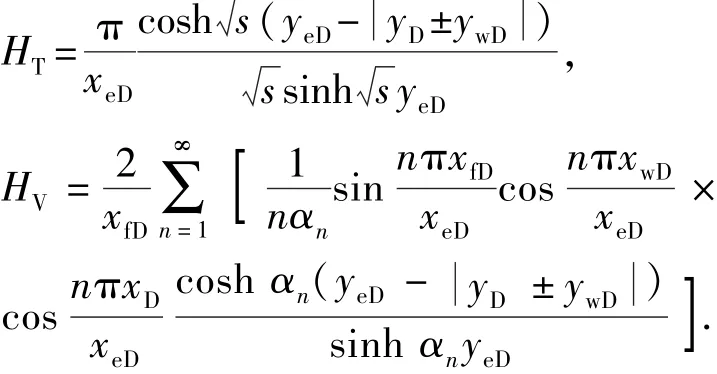
Cinco-Ley［19］和Al-Kobaisi［20］先后利用不同的数值方法获得了有限导流裂缝的压力动态，但解法复杂且计算量大，不易推广使用。借助文献［21］和［22］研究思路，将裂缝导流能力看作一种表皮，起增加额外压力降落的作用，有限导流裂缝分解为无限导流裂缝解与有限导流函数的复合解，

Blasingame［21］给出了三线性流模型（相当于有限导流函数）与无限导流模型的复合解，三线性流模型能够模拟早期的裂缝线性流和双线性流阶段，无限导流解能够较好地模拟地层线性流和拟径向流阶段，但复合解难以模拟有限导流裂缝从双线性流过渡到拟径向流时缺失的地层线性流阶段。

针对这个问题，Wilkinson［23］首先给出了低导流裂缝压力解，随后将裂缝置于其端点处存在不渗透边界的地层中，利用Fourier变换方法解析求解出低导流裂缝的早期流动（裂缝线性流、双线性流）特征函数，处理变换后形式为

基于渐近拟合分析法［24］给出拟合公式，用以修正晚期双线性流与地层线性流耦合过程中的过渡流阶段；基于数值模拟结果，引入校正函数改进复合解的精度，

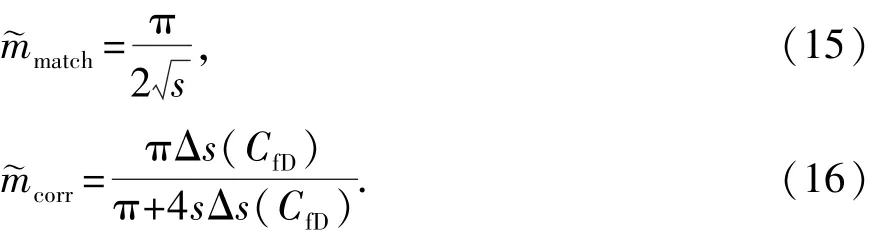
最终的有限导流函数可表述为

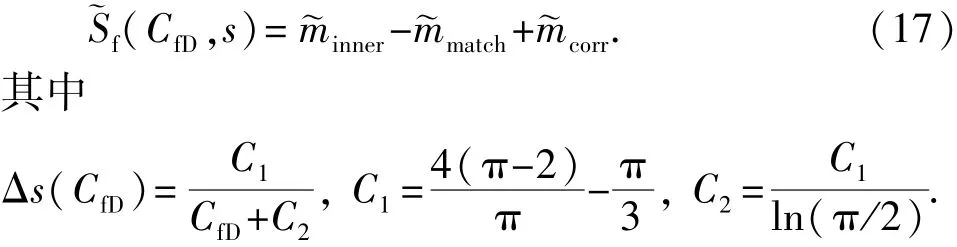
利用无限导流与均匀流量裂缝间的转换关系［25］，令式（12）中的 xD=xwD+0.732xfD，结合式（17）即可得到有限导流裂缝的不稳态空间压力分布，

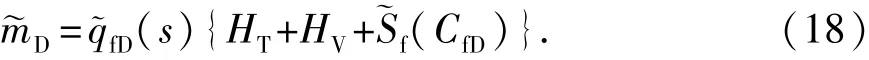
研究表明，定产条件下的压裂水平井在拟稳态阶段单裂缝流量趋于稳定［26］，不随时间变化。在拟稳态阶段，式（12）中的Laplace产量退化为qfD/s，利用s趋近∞渐近分析式，结果为

同时在Laplace空间内对式（17）做拟稳态流动渐近分析（s趋近∞），得到有限导流因子拟稳态表达式为

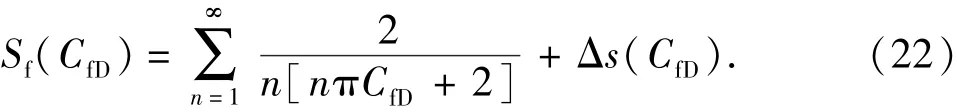
Wang等［28］在王晓冬等［11，18］研究成果基础上，利用边界元数值方法（BEM）计算了有限导流裂缝的半解析压力解，通过数据回归给出了拟稳态阶段的有限导流因子为

其中

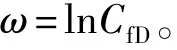
式（23）是数据回归公式，无具体物理意义，但使用简洁方便。Wang等在其文献［28］中以 Riley［29］提出的全解析导流能力影响因子模型为基础，对式（23）进行了仔细地计算对比，获得了满意的拟合效果，因此式（23）可作为可靠的对比标准。对比分析式（22）与式（23），结果表明从低导流能力到高导流能力两种方法拟合效果良好（图1），表明本文中推导的有限导流因子可靠。

图1 有限导流因子验证分析Fig.1 Validation analysis of finite diversion factor

1.2 有限导流压裂水平井拟稳态产能模型

在拟稳态阶段，定容气藏物质平衡方程满足：

与垂直裂缝中单一线性流相比，横向压裂缝在井筒附近产生一个附加压力降，通常用聚流表皮因子［7］修正：

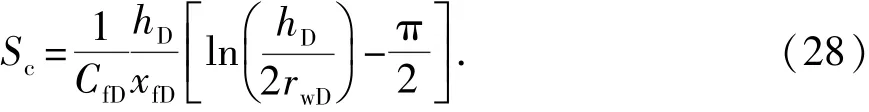
根据势叠加原理，地层任意点处的压降等于各裂缝单独工作时在该点引起的压降总和（图2）。这样可获得井筒与裂缝i交叉点处压力值mwDi，

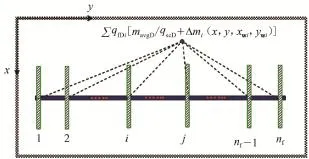
图2 压裂水平井势叠加示意图（俯视面）Fig.2 Top sketch of multiple fractured horizontal well

假设井筒具有无限导流能力，即 mwD1=mwD2=…=mwDnf，结合流量约束条件∑qfDi=qscD=1可以获得nf×nf阶的nf段压裂水平井产能计算模型为

式中，IPi为第i条裂缝的无量纲产能系数；mDij为第j条裂缝在第i条裂缝上引起的单位产量下的压降。

式（30）表明裂缝i的有限导流因子和聚流表皮影响只体现在流体从裂缝i流入井筒过程中形成的附加压降，对其他裂缝的流动过程不产生影响［18，31］。式（30）可以借助Newton迭代算法数值求解。从式（30）可知，裂缝的无量纲导流能力CfD、条数nf、半长xf、相对位置（xwD，ywD）都会影响气井产能；压裂参数与给定地层间存在着最佳匹配关系，优化这种关系能够降低缝间干扰，减小地层封闭影响，增大裂缝与地层接触面积，平衡裂缝流入流出动态，提高气井产能。为方便讨论，涉及到的压裂水平井各裂缝参数均一致，即裂缝长度、导流能力、裂缝间距等相等。

2 气井产能优化

2.1 优化裂缝布局

裂缝布局主要包括裂缝条数（nf）、裂缝穿透率（Ix=2xf/xe）、压裂段穿透率（Iy=Lf/ye，Lf为最外侧两条裂缝间距），这些压裂参数决定着裂缝系统与地层的接触面积、与封闭边界的相互作用以及裂缝间的相互干扰。图3反映了气井产能 （IP=∑IPi）随裂缝条数、压裂段穿透率的变化规律，可从两种角度进行分析。

（1）固定压裂段穿透率Iy。增加裂缝条数增大了压裂水平井与地层接触面积，同时也加剧了裂缝间相互干扰，但整体上减小了渗流阻力，提高了气井产能。

（2）固定裂缝条数nf。当nf≥14时裂缝条数较多，有效增加了压裂水平井与地层的接触面积，掩盖了裂缝间相互干扰的影响。在此基础上增大压裂段穿透率可以有效缓解裂缝间相互干扰，进一步减小渗流阻力，所以压裂段穿透率越大对应的气井产能越高；当nf≤13时裂缝条数较少，接触面积增大产生的“正”影响不足以完全弥补裂缝间相互干扰产生的“负”影响，此时压裂参数间存在最佳匹配问题。

定量分析图3（a）可得到不同裂缝条数对应的最优压裂段穿透率，结果见表1。

表1 裂缝条数对应的近似最优压裂段穿透率Table 1 Fracture number corresponding to optimum fracture penetration ratio

为进一步分析，计算不同裂缝条数对应的产能随压裂段穿透率的变化（图4）。图4反映不同裂缝条数对应不同最优压裂段穿透率，拟合裂缝条数nf、最优压裂段穿透率Iyopt离散点可获得二者间的近似关系式：

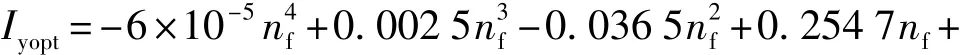
图3 气井产能随压裂段穿透率及裂缝数变化Fig.3 Variation of dimensionless productivity index with fractured horizontal wellbore penetration ratio and fracture number

经过渐近分析可知，式（31）满足近似关系式：

式（32）有明确物理意义：在缝间干扰与边界封闭作用的共同影响下，相邻裂缝间形成分流线，将裂缝系统间隔成一系列具有不同泄流面积的单缝［30］。当每条裂缝对应的泄流面积相等时，裂缝间干扰最小、边界封闭影响最低、单裂缝产能相同、气井产能最大。Iy＜Iyopt时外侧裂缝对应泄流面积较大、单缝产能较高，Iy＞Iyopt情况则与之相反（图4）。

以苏里格压裂水平井为例说明确定最优裂缝条数的流程。目前苏里格气藏典型的南北向水平井段长1000 m，东西向排距600 m（即xeD：yeD=0.3），按均匀布缝原理（式（32））沿水平井筒进行压裂。计算不同裂缝穿透率对应的气井产能关于裂缝条数的导数值（图5）。其中导数最大值对应的裂缝条数为最优裂缝条数nfopt，气井能够在此范围内较为显著地达到较高的产能。同样通过数据拟合可获得裂缝最优条数nfopt与Ix的函数关系式。

图4 气井产能随压裂段穿透率的变化Fig.4 Variation of dimensionless productivity index with fractured horizontal wellbore penetration ratio

对式（33）和（34）进行积分平均可得到最优裂缝条数参考值为

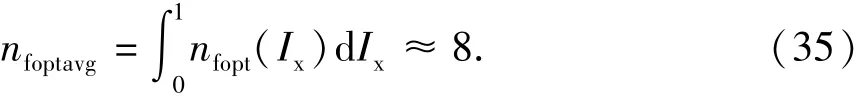
对应的裂缝穿透率为 Ix=0.53。须强调的是，式（33）～（35）计算结果受气藏泄流面积的几何规模（xeD/yeD）影响。

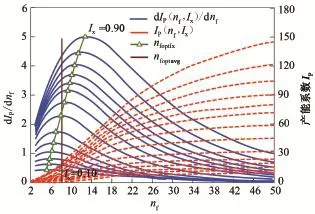
图5 裂缝均匀分布下的气井产能优化图版（xeD/yeD=0.3）Fig.5 Optimization curves of dimensionless productivity index in configuration of equally spaced fracture（xeD/yeD=0.3）

2.2 优化导流能力

将无量纲裂缝导流能力定义改写为如下形式：

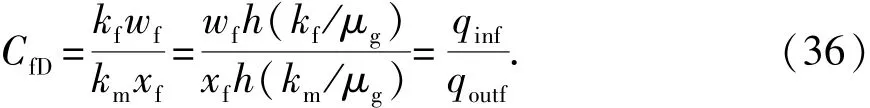
式（36）反映了裂缝的流入量与流出量比值，如果流入量能够匹配流出量，裂缝将达到最佳导流状态，此时裂缝导流能力对气井产能的影响降到最低。

为了能在一定的参数变化范围内较快地达到较高的产能水平，计算气井产能与裂缝导流能力、穿透率的关系图版，同时计算产能关于导流能力对数的导数，得到新型分段压裂水平井产能优化图版（图6）。

由图6可知，随着裂缝穿透率的变化，最优导流能力发生变化，通过回归可以得到裂缝穿透率与最优导流能力的关系式为

对CfDopt取积分平均得到最优导流能力参考值为

图6 新型压裂水平井导流能力优化图版（xeD/yeD=0.3，nf=8）Fig.6 New type optimization curves of productivity index（xeD/yeD=0.3，nf=8）

式（38）计算值与Economides［32］给出的最佳无量纲导流能力值1.6相近，验证了本文算法的合理性。须强调的是，在裂缝布局最优的情况下压裂水平井可等效为一系列的单裂缝，对应单缝泄流面积的几何形状为（xeye/nf），此时裂缝导流能力的优化函数关系（式（37））随地层长度与宽度比ye/xe、裂缝条数nf的变化而发生改变。

综上所述，合理使用式（32）～（34）、（37）、（38）的步骤如下：

（1）根据气井的有效控制面积确定气藏矩形长宽比。

（2）利用式（32）中压裂段穿透率与裂缝条数的最优关系获得裂缝穿透率与裂缝条数的优化关系线，式（33）和图5，然后利用式（34）得到最优裂缝条数参考值和对应的裂缝穿透率。

（3）根据特定的矩形长宽比和裂缝条数参考值确定裂缝穿透率与导流能力的优化关系线，式（37）和图6，同时利用式（38）得到最优导流能力参考值。

（4）实际应用时可以选取最优参数关系线附近的一个小条带区域作为优化压裂参数的参考区域。在最优参数的作用下气井能够较为显著地达到较高的产能水平。

3 结 论

（1）利用积分变换、渐近分析、势叠加、附加导流因子等方法能有效地建立考虑边界封闭影响的有限导流压裂水平井拟稳态产能计算模型，其中裂缝条数、长度、导流能力、压裂段长度以及地层几何规模、裂缝相对分布均会对气井产能产生影响。

（2）提高气井产能主要通过减小缝间干扰、降低边界封闭作用、增大裂缝与地层接触面积、平衡裂缝与地层的流入流出关系实现，当裂缝系统中各裂缝对应的泄流面积相同时，缝间干扰最小、边界封闭影响最低。

（3）对于实际生产，气井能在一定压裂参数变化范围内较快地达到较高的产能水平更具现实意义。通过求解产能关于压裂参数的导数极大值得到最优压裂参数分布线，利用积分平均的方法获得压裂参数的优化参考值。

（4）该方法主要适用于生产时间较长、已达到井间干扰或地层边界干扰阶段的压裂水平井产能优化问题，即完全进入拟稳态生产阶段。

［1］ 郝明强，王晓冬，胡永乐.压敏性特低渗透油藏压裂水平井产能计算［J］.中国石油大学学报（自然科学版），2011，35（6）：99-104. HAO Mingqiang，WANG Xiaodong，HU Yongle.Productivity calculation of multi-fractured horizontal well in ultra-low permeability pressure-sensitive reservoirs［J］. Journal of China University of Petroleum（Edition of Natural Science），2011，35（6）：99-104.

［2］ 王本成，贾永禄，李友全，等.多段压裂水平井试井模型求解新方法［J］.石油学报，2013，34（6）：1150-1156. WANG Bencheng，JIA Yonglu，LI Youquan，et al.A new solution of well test model for multistage fractured horizontal well［J］.Acta Petrolei Sinica，2013，34（6）：1150-1156.

［3］ 周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999：123-135.

［4］ 樊冬艳，姚军，姚婷，等.基于自适应遗传算法的压裂水平井参数优化［J］.油气地质与采收率，2011，18（5）：85-89. FAN Dongyan，YAO Jun，YAO Ting，et al.Parameters optimization for fractured horizontal wells based on adaptive genetic algorithm［J］.Petroleum Geology and Recovery Efficiency，2011，18（5）：85-89.

［5］ RANGHVAN R S，CHEN C C，AGAEWAL B.An analysis of horizontal wells intercepted by multiple fractures［J］.SPE Journal，1997，2（3）：235-245.

［6］ CHEN C C，RAGHAVAN R S.A multiply fractured horizontal well in a rectangular drainage region［J］.SPE Journal，1997，2（4）：455-465.

［7］ 郝明强，胡永乐，李凡华.特低渗透油藏压裂水平井产量递减规律［J］.石油学报，2012，33（2）：269-273. HAO Mingqiang，HU Yongle，LI Fanhua.Production decline laws of fractured horizontal wells in ultra-low permeability reservoirs［J］.Acta Petrolei Sinica，2012，33（2）：269-273.

［8］ 姚军，刘丕养，吴明禄.裂缝性油气藏压裂水平井试井分析［J］.中国石油大学学报（自然科学版），2013，37（5）：107-114. YAO Jun，LIU Piyang，WU Minglu.Well test analysis of fractured horizontal well in fractured reservoir［J］.Journal of China University of Petroleum（Edition of Natural Science），2013，37（5）：107-114.

［9］ 宁正福，韩树刚，程林松，等.低渗透油气藏压裂水平井产能计算方法［J］.石油学报，2002，23（2）：68-72. NING Zhengfu，HAN Shugang，CHENG Linsong，et al. Productivity calculation method of fractured horizontal wells in low permeability oil or gas field［J］.Acta Petrolei Sinica，2002，23（2）：68-72.

［10］ WANG X D，LI G H，WANG F.Productivity analysis of horizontal wells intercepted by multiple finite-conductivity fractures［J］.Petroleum Science，2010，7：367-371.

［11］ 王晓冬，张义堂，刘慈群.垂直裂缝井产能及导流能力优化研究［J］.石油勘探与开发，2004，31（5）：78-81. WANG Xiaodong，ZHANG Yitang，LIU Ciqun.Productivity evaluation and conductivity optimization for vertically fractured wells［J］.Petroleum Exploration and Development，2004，31（5）：78-81.

［12］ 罗万静，王晓冬，李凡华.分段射孔水平井产能计算［J］.石油勘探与开发，2009，36（1）：97-102. LUO Wanjing，WANG Xiaodong，LI Fanhua.Productivity of horizontal wells with segmental perforation［J］. Petroleum Exploration and Development，2009，36（1）：97-102.

［13］ 曾凡辉，郭建春，何颂根，等.致密砂岩气藏压裂水平井裂缝参数的优化［J］.天然气工业，2012，32（11）：54-60.ZENG Fanhui，GUO Jianchun，HE Songgen，et al.Optimization of fracture parameters of fractured horizontal wells in tight sandstone gas reservoirs［J］.Natural Gas Industry，2012，32（11）：54-60.

［14］ 曲占庆，曲冠政，何利敏，等.压裂水平井裂缝分布对产能影响的电模拟实验［J］.天然气工业，2013，33（10）：1-7. QU Zhanqing，QU Guanzheng，HE Limin，et al.The impact of fracture distribution on the productivity of a fractured horizontal well：a study based on electrolytic analogy experiments［J］.Natural Gas Industry，2013，33（10）：1-7.

［15］ 柳毓松，廉培庆，同登科，等.利用遗传算法进行水平井水平段长度优化设计［J］.石油学报，2008，29（2）：296-299. LIU Yusong，LIAN Peiqing，TONG Dengke，et al.Optimum design of the horizontal section length in a horizontal well using genetci algorithm［J］.Acta Petrolei Sinica，2008，29（2）：296-299.

［16］ 刘珊，同登科.水平井分段采油优化模型［J］.计算力学学报，2010，27（2）：342-346. LIU Shan，TONG Dengke.The optimization models of horizontal wells with separated production scheme［J］. Chinese Journal of Computational Mechanics，2010，27（2）：342-346.

［17］ OZKAN E，RAGHAVAN R.New solutions for well-test analysis problems：part1：analytical consideration［R］. SPE 18303，1991.

［18］ 王晓冬，罗万静，侯晓春，等.矩形油藏多段压裂水平井不稳态压力分析［J］.石油勘探与开发，2014，41（1）：74-78. WANG Xiaodong，LUO Wanjing，HOU Xiaochun，et al.Transient pressure analysis of multiple-fractured horizontal wells in boxed reservoirs［J］.Petroleum Exploration and Development，2014，41（1）：74-78.

［19］ CINCO-LEY H，SAMANIEGO V F，DOMINGUEZ A N. Transient pressure behavior for a well with a finite conductivity vertical fractures［R］.SPE 6014，1976.

［20］ AL-KOBAISI M，OZKAN E，KAZEMI H.A hybrid numerical/analytical model of finite-conductivity vertical fracture intercepted by a horizontal well［R］.SPE 92040，2006.

［21］ BLASINGAME T A，POE B D.Semi-analytic solutions for a well with a single finite-conductivity vertical fracture［R］.SPE 26424，1993.

［22］ BROWN M，OZKAN E，RAGHAVAN R，et al.Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs［R］. SPE 125043，2009.

［23］ WILKINSON D J.New results for pressure transient behavior of hydraulically fractured wells［R］.SPE 18950，1989.

［24］ VAN D M.Perturbation methods in fluid mechanics［M］. California：Parabolic Press，1975.

［25］ GRINGARDEN A C，RAMEY H J，RAGHAVAN R. Unsteady-state pressure distributions created by a well with a single infinite-conductivity vertical fracture［R］. SPE 4051，1972.

［26］ ZERZAR A，BETTAM Y.Interpretation of multiple hydraulically fractured horizontal wells in closed systems［R］.SPE 84888，2003.

［27］ 孔祥言.高等渗流力学［M］.合肥：中国科技大学出版社，2010.

［28］ WANG L，WANG X D，DING X M，et al.Rate decline curves analysis of a vertical fractured well with fracture face damage［J］.Journal of Energy Resource Technology，2012，134（3）：1-9.

［29］ RILEY M F，BRIGHAM W E，HORNE R N.Analytic solutions for elliptical finite-conductivity fractures［R］. SPE 22656，1991.

［30］ 王军磊，贾爱林，何东博，等.致密气藏分段压裂水平井产量递减规律及影响因素［J］.天然气地球科学，2014，25（2）：278-285. WANG Junlei，JIA Ailin，HE Dongbo，et al.Rate decline of multiple fractured horizontal well and influence factors on productivity in tight gas reservoirs［J］.Natural Gas Geoscience，2014，25（2）：278-285.

［31］ ZERZAR A，BETTAM Y.Interpretation of multiple hydraulically fractured horizontal wells in closed systems［R］.SPE 84888，2003.

［32］ ECONOMIDES M，OLIGNEY R，VALKO P.Unified fracture design：bridge the gap between theory and design［M］.Texas：Orsa Press，2002.

（编辑 李志芬）

Pseudo steady productivity evaluation and optimization for horizontal well with multiple finite conductivity fractures in gas reservoirs

WANG Junlei，JIA Ailin，WEI Yunsheng，ZHAO Wenqi
（PetroChina Research Institute of Petroleum Exploration&Development，Beijing 100083，China）

The fracture boundary with no flowing through has a significant influence on productivity evaluation and fracturing parameter optimization in a pseudo steady state（PSS）.In this paper，the solution of pressure distribution in the PSS in a single hydraulic fracture with finite conductivity was derived incorporating an integral transformation method，and a novel productivity model of a multiple fractured horizontal well（MFHW）within rectangular formation was presented in coupling with material balance equation and pressure superposition.The model was solved using a Newton numerical iteration method.The model was used to calculate the productivity of a MFHW with regard to different fracturing parameters，and the corresponding optimum relationships were established by regressing the maximum derivatives of productivity with different fracturing parameters.The results show that the productivity of a MFHW is determined by the number of fractured sections，the spacing，length，conductivity and configuration of the fracture.The productivity can be enhanced via stimulating more fractures，reducing the interaction between fractures，restraining the no flow effect of fracture boundaries，and matching the inflow rate with that of the outflow rate of the fractures.The configuration of equally spaced multiple fractures is the optimal condition for fracture arrangement，and the optimum relation of dimensionless conductivity varies with the changes of length-width ratio and the fracture number.In practical application，a narrow parameter range around the optimum values should be selected as areference for optimizing the fracturing parameters.

horizontal well；finite conductivity；pseudo steady state；dimensionless productivity index；parameter optimization

TE 312

A

1673-5005（2016）01-0100-08 doi：10.3969/j.issn.1673-5005.2016.01.014

2015-03-10

国家科技重大专项（2011ZX05015）

王军磊（1986-），男，工程师，博士，研究方向为渗流力学及气藏工程。E-mail：williamwang_2@126.com。

引用格式：王军磊，贾爱林，位云生，等.有限导流压裂水平气井拟稳态产能计算及优化［J］.中国石油大学学报（自然科学版），2016，40（1）：100-107.

WANG Junlei，JIA Ailin，WEI Yunsheng，et al.Pseudo steady productivity evaluation and optimization for horizontal well with multiple finite conductivity fractures in gas reservoirs［J］.Journal of China University of Petroleum（Edition of Natural Science），2016，40（1）：100-107.