断层对煤层水力压裂裂缝扩展的影响

夏彬伟，杨 冲，卢义玉，宋晨鹏，葛兆龙

（1.重庆大学煤矿灾害动力学与控制国家重点实验室，重庆400030；2.重庆大学复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆400030）

断层对煤层水力压裂裂缝扩展的影响

夏彬伟1，2，杨 冲1，2，卢义玉1，2，宋晨鹏1，2，葛兆龙1，2

（1.重庆大学煤矿灾害动力学与控制国家重点实验室，重庆400030；2.重庆大学复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆400030）

针对煤层中的次生断层或小型滑移断层会影响水力裂缝扩展方向的问题，通过建立压裂裂缝遇断层的二维模型，采用理论分析和数值模拟方法分析逼近角度、水平主应力差、煤岩体弹性模量差异等因素对水力裂缝扩展方向的影响规律，建立裂缝穿过断层形成有效压裂的判断准则，在给定煤岩体参数条件下，拟合出水力裂缝穿过断层形成上下盘煤层贯通裂缝的逼近角度-水平主应力差的临界曲线。结果表明：逼近角度、水平主应力差、煤岩体弹性模量是影响压裂裂缝走向的主要因素，在低主应力差、较小逼近角度、较高顶板弹性模量的情况下，断层面易产生张开型破坏；当逼近角度-应力差坐标点位于曲线上方时裂缝将穿过断层面进入顶板，当角度-应力差坐标点位于曲线下侧时断层面张开裂缝将扩展至下部煤层形成上下盘煤层贯通裂缝。

煤层；滑移断层；水力裂缝；裂缝扩展

水力压裂作为最早使用在油、气田开发［1-2］以及深部应力［3］测量的关键技术，近年来被应用于煤矿井下瓦斯增透，钻孔深入煤体经过水力压裂后，能扩大其有效影响半径，改善周围煤体透气性，为矿井瓦斯有效抽采创造良好条件。由于深部煤层地质条件复杂，当水力裂缝扩展过程中遇到小型滑移断层或次生断层时，受逼近角度、水平主应力差、煤岩体弹性模量等因素的影响，极可能导致裂缝扩展方向发生偏转，不能对煤层实现有效压裂，严重影响煤层增透效果及范围。对于油气储层，一些学者对产层中岩性突变体以及天然裂缝对水力裂缝水平扩展的影响做了相关研究。Anderson等［4］发现存在一个以临界正应力表示的临界界面剪切强度，高于此值，裂缝将可能穿过界面，反之裂缝将沿界面产生滑动，不会穿过界面。Heuze等［5］发现，水力裂缝扩展方向平行于不连续面时，水平应力差和不连续面之间弹性模量的差异性会导致裂缝扩展方向的偏转。Murphy等［6］认为岩石破裂是剪切应力作用的结果，针对节理性岩层，岩石压裂是岩体沿节理面的剪切滑移。门晓溪等［7］模拟分析了不同层理角度及不同岩石强度的非均质层理岩体在孔隙水压力作用下的水压致裂过程。张然等［8］建立了水力裂缝穿过天然裂缝的判断准则，且给出了水力裂缝穿出天然裂缝角度的计算方法。陈勉和金衍等［9］通过室内物理模拟实验研究发现，法向应力对水力裂缝能否穿过突变体起着决定性作用。笔者在上述研究的基础上建立水力裂缝遇小型滑移断层和次生断层的力学模型，采用理论分析结合RFPA2D-Flow数值模拟，分析断层面逼近角度、水平主应力差、断层面两侧煤岩体弹性模量等因素对水力裂缝扩展的影响，并建立水力裂缝遇断层形成有效压裂的判断准则。

1 裂缝扩展机制

1.1 裂缝遇断层模型

当煤层赋存深度大于300～600 m时，水力压裂通常形成垂直于最小水平主地应力方向的垂直裂缝［10］。当裂缝扩展至断层时，可将实际模型简化如图1所示。由于裂缝三向扩展，当裂缝扩展至断层面，压裂液大量进入断层面克服断层面法向应力致使其张开时，裂缝扩展将出现以下3种情况：

（1）裂缝直接穿过断层面进入顶板，继续沿最大水平主应力方向扩展。

（2）断层面端部产生剪切破坏，裂缝沿着断层面扩展，裂缝不发生转向仍然沿断层面扩展。

（3）断层面张开，断层面端部不产生剪切破坏，裂缝从下部煤层起裂扩展（为方便描述，以下称之为有效压裂）。

图1三维煤层压裂模型Fig.1 Three-dimensional model of coal seam fracturing

1.2 扩展临界水压分析

目前，采用井下水力压裂技术的煤层埋深普遍大于400 m。深度大于300～600 m的水力压裂通常形成垂直于最小水平主地应力方向的垂直裂缝，由于上下围岩层强度明显大于煤层，裂缝不能突破上下围岩，从而形成恒高椭圆截面缝，因此在研究裂缝扩展规律问题时不考虑裂缝高度的扩展，通常简化为二维模型研究裂缝的水平方向扩展规律。本研究涉及：①扩展至上部煤层与断层面交界面时断层面是否张开；②断层面张开时端部是否产生剪切破坏。笔者拟将所述问题分解为两个水平剖面进行平面问题单独依次分析，即A-A剖面（图2）和B-B剖面（图3），图中θ为水平面上最大主应力方向与断层面之间的逼近角。

据此，对图2所示模型，此时裂纹走向将会出现两种情况：①裂缝直接穿过断层面进入顶板；② 缝内水压克服断层面法向应力产生张开。

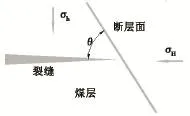
图2 剖面A-A平面模型Fig.2 Section of A-A plane model

根据裂缝扩展理论，在其他条件相同的情况下，线性裂缝扩展所需流体压力最小，则当水力裂缝缝端压力为

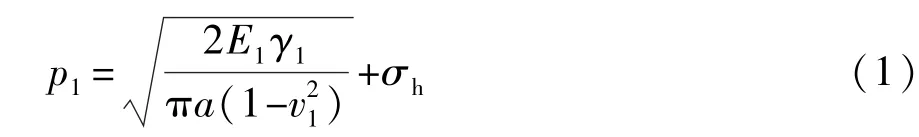
时，裂缝在煤层中起始扩展。同理，当水力裂缝缝端压力为

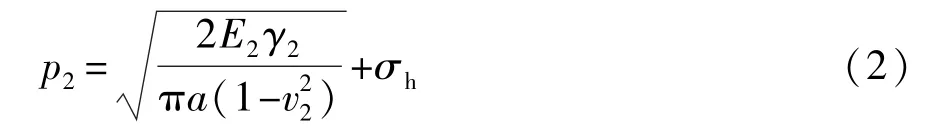
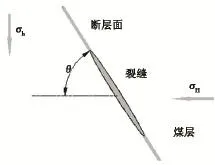
图3 剖面B-B平面模型Fig.3 Section of B-B plane model

1.3 断层面的张开

当压裂裂缝与断层面相交，裂缝延伸尖端的流体压力p大于断层面上的正应力σn时，断层面便会张开。即判断断层面张开的临界状态表示为

在断层面张开发生膨胀，流体压力在下降一段时间后继续增加，随着断层面内水压的持续增加，裂缝将沿着断层面继续延伸。

假定裂缝的变形破坏为线弹性行为，根据二维线弹性理论［12］，断层面的剪切应力σt和正应力σn表示为

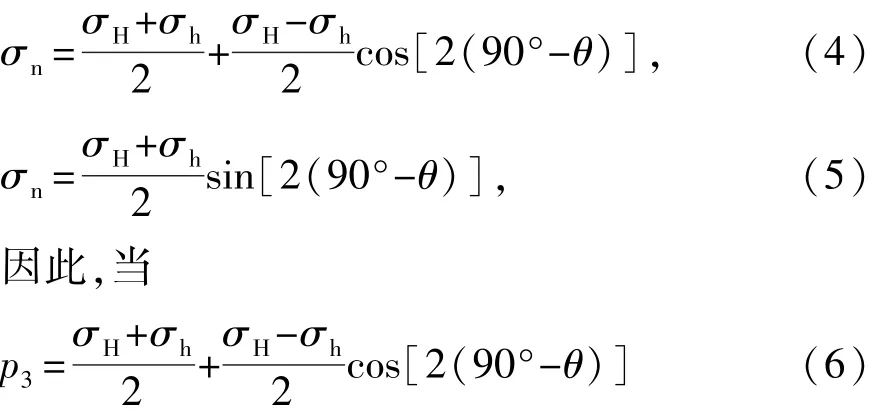
时，断层面将产生张开性破坏。

1.4 沿断层面的剪切破坏

作用于断层面的剪切应力过大很容易产生剪切滑移，此时裂缝将沿着断层面扩展。作用在断层面近壁面上的正应力和剪应力有如下关系：

式中，c0为岩体的黏聚力，MPa；τ为作用于断层面的剪切应力，MPa；Kf为断层面的摩擦因数；p0为断层面近壁面的流体压力，MPa。

因此当

时，断层面就会产生剪切性的滑移。当扩展中的裂缝与断层面相交后，由于水力裂缝缝尖端已经和断层面孔隙连通，压裂液大量进入断层面，断层面近壁面的液体压力为

式中，p为断层面剪切破坏之前裂缝内最大水压。

将式（4）、（5）和（9）代入式（8）后整理得

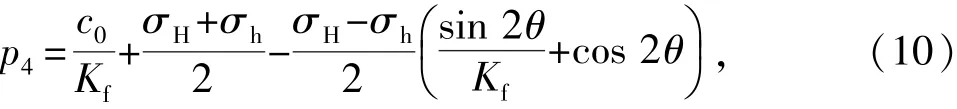
即当缝内水压达到剪切破坏临界值p4时，断层面将产生剪切破坏。

1.5 裂缝扩展方向

（1）当p3＞p2，即

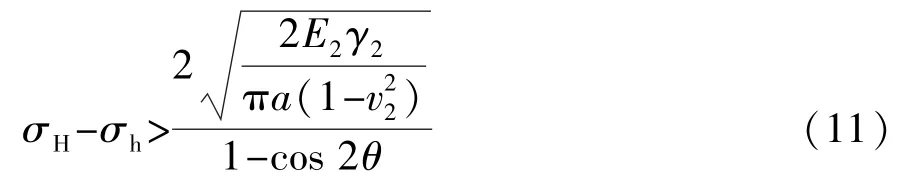
时，断层面将不会张开，裂缝将直接穿过断层面进入顶板扩展，如图4所示。

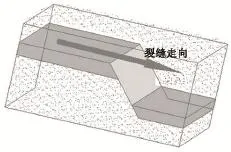
图4 裂缝穿过断层面Fig.4 Crack propagation through fault plane

由重庆某矿地层资料和实验可得顶底板弹性模量为30 GPa，顶底板泊松比为0.20，顶底板裂缝半长为1 m，裂缝表面能为0.0004 MPa.m，断层面摩擦系数为0.8。由此得到断层面张开边界曲线见图5。

（2）当p2＞p3且p1＜p4，即

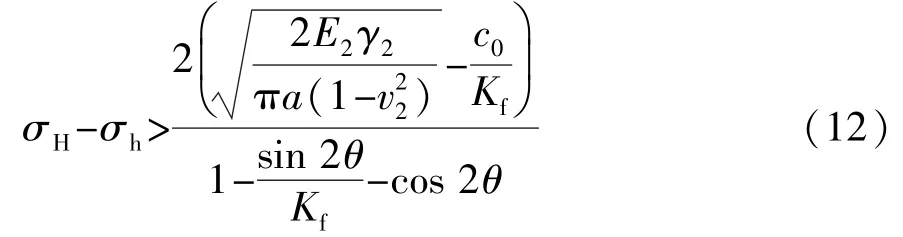
时，断层面将张开且断层面不会产生剪切破坏，裂缝将进入下部煤层扩展，如图6所示。

当p2＞p3且p1＞p4时，断层面张开，裂缝将沿断层面产生剪切破坏，如图7所示。

由p1、p2、p3及p4表达式可知，裂缝尖端在煤岩体中起裂压力与煤岩体弹性模量、泊松比以及σh相关，且p2恒大于p1，p3与σH、σh及逼近角度相关，且由式（11）可以看出，在煤岩体力学参数一定的条件下，当裂缝扩展至断层面时裂缝的走向由水平主应力差以及逼近角度决定，裂缝在扩展至断层面时，较大应力差易导致裂缝穿过断层面，并且随着逼近角度θ（θ∈［0，π/ 2］）递增，裂缝愈发趋于穿过断层面。对式（12）进行函数极值分析可知，当断层面张开后受地应力及煤岩参数影响裂缝进入下部煤层扩展的趋势明显大于断层面产生剪切破坏的趋势，即形成有效压裂。

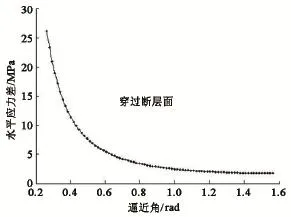
图5 断层面张开边界曲线Fig.5 Critical curve of fault plane opening

图6 裂缝沿界面进入下部煤层Fig.6 Crack along interface into lower coal seam

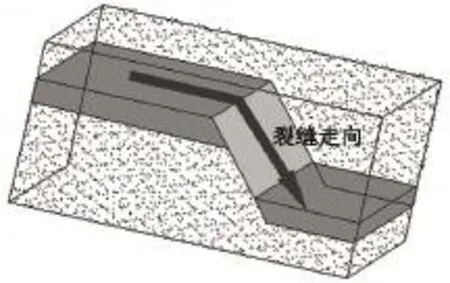
图7 裂缝沿界面延伸Fig.7 Cracks along interface

2 数值模拟

2.1 剖面A-A数值分析

2.1.1 水平主应力差和相交角的影响

采用岩石真实破裂过程分析的渗流应力耦合分析系统RFPA2D-Flow［13］对水力压裂过程中水平主应力差和断层与最大水平主应力方向的相交角θ等的影响进行分析。由于煤层在整个压裂过程中在铅垂方向上的位移受到各上覆岩层的限制，相对于水平方向上的位移很小，可以忽略不计，因此将该模型视为平面应变模型。建立边长为10 m×10 m的正方形区域，划分为300×300=90000个单元，对水力裂缝进行平面剖切。在模型的中部开挖一长轴为1 m、短轴为0.2 m的椭圆表示水力裂缝，如图8所示，图中蓝色部分表示煤层，绿色部分表示顶板，另外在煤岩交界面中部采用线开挖长为4 m的空洞表示断层面。

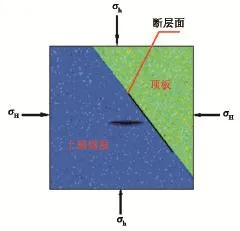
图8 剖面A-A数值模型Fig.8 Profile A-A numerical model

模型所受的水平地应力以位移边界条件的形式施加于模型的四周。由理论可知，裂纹初始扩展将沿最小水平主应力的垂直方向扩展，因此，在模型左右、上下两侧分别施加最大、最小水平主应力σH、σh。然后注入水压作用于模型水力裂缝的内壁面，水头压力以0.3 MPa的单步增量递增，初始水压p0根据不同模型的初始边界条件而定，模型煤层与岩层均质度均为3。根据上部煤层赋存特征，共进行12组模拟，水平地应力及相交角的参数见表1。

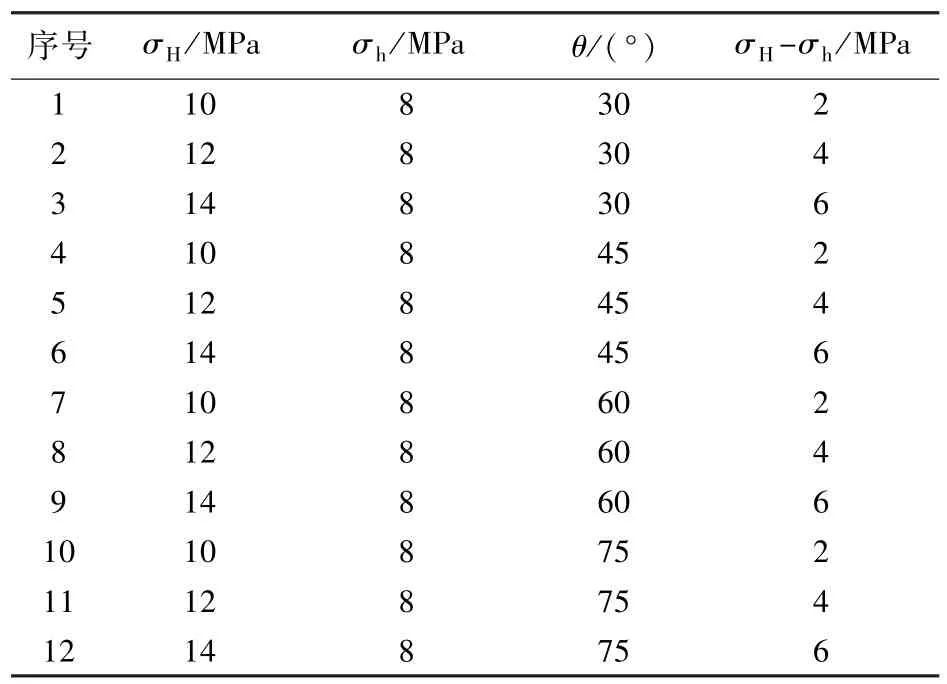
表1 水平主应力差和逼近角参数Table 1 Parameters of horizontal differential principal stress and angle of interaction

目前重庆矿区大多煤岩赋存深度600～700 m，煤岩体力学参数见表2。

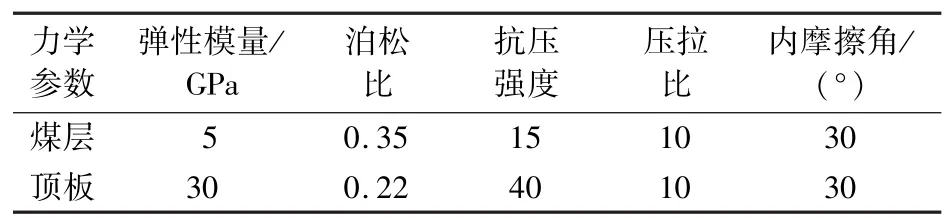
表2 煤体力学参数Table 2 Mechanical parameters of coal and rock

模拟结果如图9所示，图中绿色部分表示应力集中区域。在逼近角为30°的（1）～（3）组模拟中，扩展中的压裂裂缝遇到断层面时一致趋于沿着断层面延伸。在逼近角为45°的3组模拟中，随着主应力差的增加，扩展的裂缝从沿断层面扩展逐渐趋于进入顶板和沿断层面扩展两种情况共存，当应力差达到6 Pa时裂缝完全穿过断层面扩展至顶板，说明随着主应力差σH-σh的增加，水力裂缝趋向穿过断层面扩展。在逼近角为60°的3组模拟中，当应力差为2 MPa时延伸裂缝在刚扩展至断层面时会沿着交界面延伸，但延伸一段距离之后又转向进入顶板延伸，并且随着主应力差的递增裂缝延伸逐渐趋向直接穿过断层面。在逼近角为75°的3组模拟中，裂缝一致趋于直接穿过断层面沿最大主应力方向扩展。

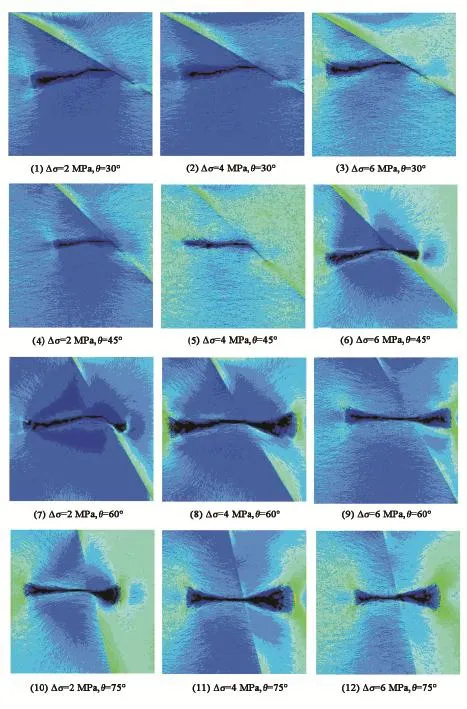
图9 压裂裂缝扩展模拟结果Fig.9 Fracturing fracture simulation results

由图9还可以得知，在相同主应力差条件下，随着相交角由30°增加到75°，延伸中的裂缝穿过断层面沿最大主应力方向扩展的趋势逐渐增加。

2.1.2 顶板岩层弹性模量E2的影响

由分析可知，顶板弹性模量值会对裂缝的走向产生影响。改变顶板岩层的弹性模量值，煤体的力学参数不改变，水平主应力与弹性模量值组合见表3。

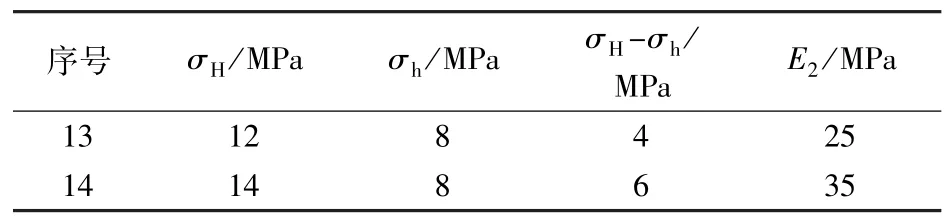
表3 水平主应力差和相交角参数Table 3 Parameters of horizontal differential principal stress and angle of interaction

2组模拟结果见图10。分别与第5、6组进行对比可知，在相同的水平主应力差下，顶板的弹性模量值越大，裂缝进入顶板扩展所需水压越接近断层面张开所需水压，此时断层面产生张开，裂缝沿断层面扩展。

图10 压裂裂缝扩展结果Fig.10 Fracturing fracture simulation results

2.2 剖面B-B数值分析

当逼近角度不超过45°时，断层面较易产生张开，只有断层面张开后才会涉及到下部层的扩展问题。相交角度和应力差是影响裂缝扩展的主要因素，建立图11所示模型，进行9组模拟（表4），其他煤岩体参数与表2一致。

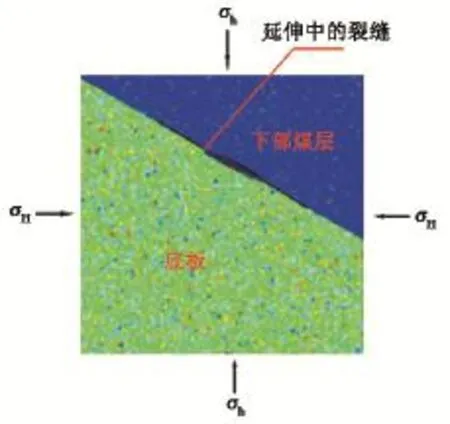
图11 剖面B-B数值模型Fig.11 Profile B-B numerical model

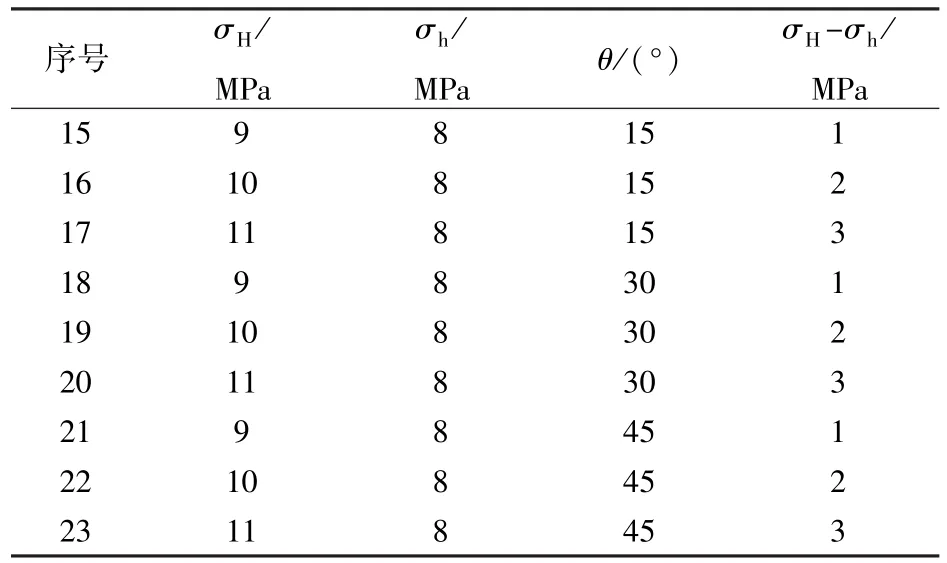
表4 水平主应力差和逼近角参数Table 4 Parameters of horizontal differential principal stress and angle of interaction

模拟结果见图12，随着主应力差与逼近角度的递增，裂缝扩展一致趋于进入下部煤层，即当断层面张开裂缝扩展至下部煤层时，裂缝将一致穿过下部煤层形成上下盘煤层贯通裂缝。

采用MATLAB拟合得到图13。

从图13看出，裂缝穿过断层面的试点均位于断层面张开边界上方，有效压裂试点大致均位于曲线下侧；在曲线上方，就某个逼近角而言，模拟点离曲线的距离代表了裂缝穿过断层面进入顶板的难易程度；逼近角、主应力差越大，裂缝越趋于穿过断层面进入顶板；当断层面产生张开性破坏时，裂缝一致进入下部煤层形成有效压裂，而不产生断层面端部的剪切性破坏。

图12 下部煤层压裂裂缝扩展模拟结果Fig.12 Lower coal seam fracturing fracture propagation simulation results

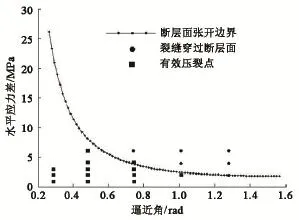
图13 压裂裂缝延伸模拟结果Fig.13 Fracturing fracture propagation simulation results

3 结 论

（1）压裂裂缝与断层面的逼近角度、水平主应力差、煤岩体弹性模量是影响压裂裂缝遇断层走向的主要因素，在低主应力差、较小相交角度、较高顶板弹性模量的情况下，断层易产生张开性破坏。

（2）当逼近角度-水平主应力差位于曲线下方时水力裂缝一致穿过断层形成上下盘煤层贯通裂缝。

（3）当断层面产生张开后，一般情况下，裂缝一致趋于进入下部煤层扩展，断层面尖端不会产生剪切破坏。

［1］ VEATCH R W.Overview of current hydraulic fracturing design and treatment technology（1）［J］.Journal of Petroleum Technology，1983，35（4）：677-687.

［2］ VEATCH R W.Overview of current hydraulic fracturing design and treatment technology（2）［J］.Journal of Petroleum Technology，1983，35（5）：853-864.

［3］ STOCK J M，HEALY J H.Continuation of a deep borehole stress measurement profile near the San Andreas Fault（2）：hydraulic fracturing stress measurements at Black Butte，Mojave Desert，California［J］.Journal ofGeophysical Research Solid Earth，1988，93（B12）：15196-15206.

［4］ ANDERSON G D.Effects of friction on hydraulic fracture growth near unbonded interfaces in rocks［J］.Society of Petroleum Engineers Journal，1981，21（1）：21-29.

［5］ HEUZE F E，SHAFFER R J，INGRAFFEA A R，et al. Propagation of fluid-driven fractures in jointed rock（1）：development and validation of methods of analysis［C］// International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts.Pergamon：1990，27（4）：243-254.

［6］ MURPHY H D，FEHLER M C.Hydraulic fracturing of jointed formations［C］//International Meeting on Petroleum Engineering.Society of Petroleum Engineers，1986.

［7］ 门晓溪，唐春安，马天辉.水压致裂作用下岩体参数对裂纹扩展影响的数值模拟［J］.东北大学学报 （自然科学版），2013，34（5）：700-703. MEN Xiaoxi，TANG Chun΄an，MA Tianhui.Numerical simulation on influence of rockmass parameters on fracture propagation during hydraulic fracturing［J］.Journal of Northeastern University（Natural Science），2013，34（5）：700-703.

［8］ 张然，李根生，赵志红，等.压裂中水力裂缝穿过天然裂缝判断准则［J］.岩土工程学报，2014，36（3）：585-588. ZHANG Ran，LI Gensheng，ZHAO Zhihong，et al.New criteria for hydraulic fracture crossing natural fractures［J］.Chinese Journal of Geotechnical Engineering，2014，36（3）：585-588.

［9］ 金衍，陈勉.岩性突变体对水力裂缝延伸影响的实验研究［J］.石油学报，2008，29（2）：300-303. JIN Yan，CHEN Mian.Experimental study on the effects of salutatory barrier on hydraulic fracture propagation of cement blocks［J］.Acta Petrolei Sinica，2008，29（2）：300-303.

［10］ 陈勉，金衍，张广清.石油工程岩石力学［M］.北京：科学出版社，2008.

［11］ BORESI A P，SCHMIDT R J，SIDEBOTTOM O M.Advanced mechanics of materials［M］.New York：Wiley，1993.

［12］ 吴家龙.弹性力学［M］.北京：高等教育出版社，2001.

［13］ 刘洪磊，杨天鸿，于庆磊，等.岩石水压致裂影响参数的仿真［J］.东北大学学报（自然科学版），2012，33（10）：1483-1486. LIU Honglei，YANG Tianhong，YU Qinglei，et al.Simulation of influence parameters during hydraulic fracturing process of rock［J］.Journal of Northeastern University（Natural Science），2012，33（10）：1483-1486.

（编辑 刘为清）

Effect of faults on hydraulic fracture propagation in coal seam

XIA Binwei1，2，YANG Chong1，2，LU Yiyu1，2，SONG Chenpeng1，2，GE Zhaolong1，2
（1.State Key Laboratory of Coal Mine Disaster Dynamics and Control，Chongqing 400030，China；2.National&Local Joint Engineering Laboratory of Gas Drainage in Complex Coal Seam，Chonqing 400030，China）

Considering the influence of sub-fault or slum fault in the coal seam on the fracture propagation of hydraulic fracturing，the effects of approximation angle，horizontal principal stress difference，and coal and rock elastic modulus difference on hydraulic fracture propagation direction were investigated using the theoretical analysis and numerical simulation in a two-dimensional physical model.The judgment criterion of forming effective fracture through the cracking passing the fracture was established.And the critical curve for the approaching angle-horizontal principal stress difference of the coal penetrating crack，which was formed by the hydraulic fracture passing the fault，was fitted out under given coal-rock mass parameters.It is found that the approximation angle，horizontal principal stress difference，and elastic modulus of coal-rock mass play the major roles on fracture direction.Under the circumstance of low principal stress difference，smaller approaching angle，and higher roof elastic modulus，the fault is easy to produce plane tensile failure.When the approaching angle-stress difference coordinate point is above the curve，the crack will pass through the fault plane into the roof.When the angle-stress difference coordinates of point is under the level curve，cracks will be extended to the lower coal seam forming upper and lower coal seam cracks.

coal seam；slump fault；hydraulic fracturing；crack propagation

TD 712

A

1673-5005（2016）01-0092-08 doi：10.3969/j.issn.1673-5005.2016.01.013

2015-08-11

国家自然科学基金项目（51104191）；长江学者和创新团队发展计划项目（IRT13043）；重庆市自然科学基金项目（cstcjjA90004）

夏彬伟（1978-），男，副教授，博士，研究方向为采矿及地下工程。E-mail：xbwei33@cqu.edu.cn。

引用格式：夏彬伟，杨冲，卢义玉，等.断层对煤层水力压裂裂缝扩展的影响［J］.中国石油大学学报（自然科学版），2016，40（1）：92-99.

XIA Binwei，YANG Chong，LU Yiyu，et al.Effect of faults on hydraulic fracture propagation in coal seam［J］.Journal of China University of Petroleum（Edition of Natural Science），2016，40（1）：92-99.