基于直升机/发动机综合模型的变旋翼转速控制研究

陈国强，杨　娟

（中航工业航空动力控制系统研究所，江苏无锡 214063）

基于直升机/发动机综合模型的变旋翼转速控制研究

陈国强，杨娟

（中航工业航空动力控制系统研究所，江苏无锡 214063）

为了实现直升机旋翼转速在宽广范围内连续变化且涡轴发动机连续提供输出轴功率，采用1种扭矩序列转移控制方案来实现该传动链。通过2台涡轴发动机和2台多级变速器与旋翼协调工作，发动机依次连接或脱开旋翼，提供旋翼转速大范围内变化，并提供旋翼连续变化的功率。在扭矩转移过程中，针对发动机扭矩强扰动问题设计了鲁棒LM I控制器+A D RC扭矩前馈补偿控制器，最后基于直升机/发动机综合模型进行数值仿真，验证了扭矩转移方案的可行性。仿真结果表明：在转移过程中的扭矩强扰动对发动机动力涡轮转速的影响较小，旋翼转速可以实现较大范围内的快速平滑变化。

变旋翼转速；扭矩序列转移；多级变速器；直升机/发动机综合模型；航空发动机

0　引言

直升机是1个多自由度、强耦合的复杂系统，通常采用旋翼转速恒定为其控制规律，以避免旋翼扭振、操纵复杂等影响系统稳定性［1］。文献［2］提出1种变旋翼转速方案，在系统稳定的前提下可显著提高直升机综合性能，如降低发动机油耗、缩短爬升时间、降低噪声等［1-5］。该方案的主要思想是采用先进的飞行控制律，在保证直升机稳定飞行的条件下，由飞行控制器寻求1个当前点最优的旋翼转速指令并传递给涡轴发动机，再通过其驱动旋翼实现转速变化，由此，在不同的飞行任务中即可获得不同的性能收益。

然而，由于涡轴发动机动力涡轮只能在狭窄的转速带内工作，且传动系统不能提供大范围连续的动力传输，因而大范围的变旋翼转速控制在工程上很难实现，如文献［6］提出1种变旋翼转速优化控制方案降低发动机油耗，其转速变化范围仅在3%左右。相关文献显示，若采用变速齿轮系统，使涡轴发动机在燃油消耗合理的情况下可实现输出轴转速（即旋翼转速）的大范围变化（50%～100%），如近年来美国研制的A160T“蜂鸟”直升机，采用双速传动齿轮箱，由电动碳基离合器控制齿轮传动系统，在保持发动机转速恒定的情况下，可实现大范围的变旋翼转速控制，且同时避免因机身结构而导致的空气动力学共振等不稳定因素［7］。

文献［8］提出了1种扭矩序列转移方案，实现了大范围内的变旋翼转速控制。其采用发动机以及旋翼的线性模型进行数字仿真，本文在其基础上，采用旋翼/发动机非线性模型对其控制方案进行数字仿真。在扭矩转移过程中，针对发动机扭矩强扰动问题设计了鲁棒LMI控制器+ADRC扭矩前馈补偿控制器。最后通过仿真试验，验证了在系统稳定的情况下，上述方案可实现直升机旋翼转速50%～100%的连续变化，同时保证涡轴发动机能够连续提供需用功率，达到了很好的控制效果。

1　变旋翼转速控制原理

对于传统的直升机，由于扭振、操控简易等方面的原因，旋翼的转速通常保持不变，涡轴发动机动力涡轮与旋翼轴是通过具有固定传动比的传动链相连，所以传统涡轴发动机的动力涡轮转速必须为常值。但是，这种保持动力涡轮转速（旋翼转速）不变的控制策略并不能充分发挥直升机/发动机综合系统的最佳效能。

一方面当直升机处于不同飞行状态时，给定的涡轮发动机转速不一定对应于发动机处于该工况下最优经济性的转速，变动力涡轮转速的发动机特性如图1所示。从图中可见，当发动机功率（Pe）降低时动力涡轮的最高效率点，也就是图中曲线的凸点，移向较低的动力涡轮转速（Ng）（图中虚线所示），因此涡轴发动机在不同工况下可以通过性能优化算法找到1个最优的动力涡轮转速［6，9］。文献［9］介绍了1种变旋翼转速串行优化方案，在保证直升机飞行状态不变的前提下，首先寻找旋翼所需最小功率的工作点，再采用发动机性能寻优手段降低发动机油耗，比起单独执行发动机性能寻优的收益更为显著。

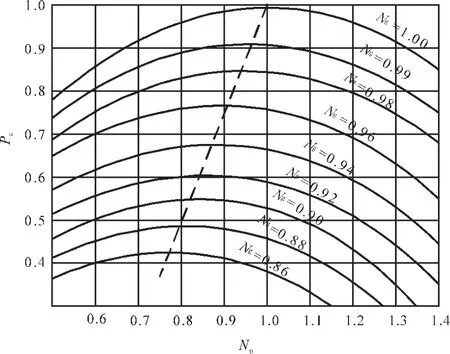
图1　变动力涡轮转速时的发动机特性

另一方面当直升机低空低速前飞时，如果将旋翼转速降低，使其小于额定100%转速，可以增加浆叶的升阻比，减小直升机前飞阻力，减小发动机输出功率，进而使得发动机燃油消耗降低，续航能力增强。

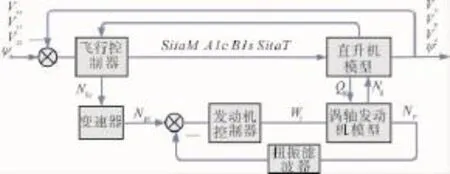
图2　直升机/发动机综合变旋翼转速控制系统

因此，在直升机/发动机综合系统中采用变旋翼转速控制方法，可以充分发挥发动机的性能，降低发动机油耗、延长直升机航程等。采用变旋翼转速的直升机/发动机综合系统结构如图2所示。首先由飞行控制器给定当前飞行状态下需求功率最小的旋翼转速指令NRr，而后将旋翼转速指令转换为动力涡轮转速指令Npr实时地传递给涡轴发动机闭环系统，发动机根据负载实时求解当前燃油输入量，得到动力涡轮转速，再经过1个固定传动比+1阶惯性环节的机械传动系统模型转化后，作为旋翼转速，进而参与直升机的飞行控制。

变旋翼转速的关键是在实现旋翼转速在宽广范围内变化时，保证涡轴发动机能够连续提供输出轴功率。根据前述内容，易采纳的变旋翼转速方案，即是1台或多台涡轴发动机与相应的多级变速箱相组合的形式，但1个关键技术问题难以克服，即当发动机变速时，旋翼与发动机脱开，而当发动机变速结束再次与旋翼连接上时，发动机输出轴转速发生跳变且与旋翼转速不同步，这样会导致输出轴功率瞬间损失，而且发动机输出轴大的转速跳变直接连接旋翼会损害变速器传动系统［10］，而且脱开离合变速过程中旋翼转速处于不受控的状态，这是难以接受的。

所采用的扭矩序列转移控制方案，通过2台涡轴发动机和2台多级变速器与旋翼协调工作，发动机依次连接或脱开旋翼，其好处在于在整个变旋翼过程中始终有至少1台发动机与旋翼轴相连，保证了旋翼转速的可控，同时又避免了发动机变速结束再次与旋翼连接上时输出轴功率瞬间损失。

在实现扭矩序列转移的过程中，即使采用上述方案，发动机动力涡轮转速仍然易受到扭矩扰动的影响，因此，如何降低动力涡轮转速由于扭矩扰动产生的下垂量，并缩短转速过渡态时间，以及如何有效控制发动机脱离与连接旋翼的时机也是变旋翼转速控制研究的1个问题。采用多变量鲁棒LMI+ADRC扭矩前馈的综合控制算法控制发动机动力涡轮转速，可以解决扭矩扰动带来的问题。

2　变旋翼转速控制实现方案

控制方案（旋翼/传动系统/双发）结构如图3所示。从图中可见，离合器是1个机械作动设备，其只允许动力涡轮驱动旋翼系统工作，反之则无效。该方案通过发动机和多级变速器与旋翼协调工作，实现旋翼转速较大范围的变化，并提供连续变化的功率给旋翼，过程如下：

（1）2台发动机同时连接旋翼共同提供旋翼需求功率；

（2）通过离合器让其中1台发动机与旋翼脱开，则其输出功率减少，由另外1台发动机提供旋翼需求功率并实现旋翼转速变化；

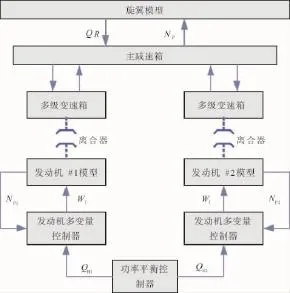
图3　旋翼/传动系统/双发结构

（3）脱开的那台发动机通过多级变速器变速，当其输出轴转速与旋翼转速再次相等时重新连接旋翼，并再次提供旋翼需求功率；

（4）对另外1台发动机进行同样的脱开操作，在变速过程中，始终保持旋翼至少与其中1台发动机相连。

以UH60黑鹰直升机/T700涡轴发动机为平台进行变旋翼转速数字仿真。实现上述扭矩序列转移方案需满足2个前提条件：（1）动力涡轮转速的工作范围为92.5%～107.5%，转速的变化为15%；（2）必须提供连续变化的扭矩给旋翼。第1点要求可以通过划分旋翼转速区间来实现，将50%～100%的旋翼转速划分为6个区间，不同区间之间有转速重叠区，每个区间的转速范围见表1。第2点要求同样满足，因为在1台发动机变速过程中，另1台发动机始终与旋翼连接。

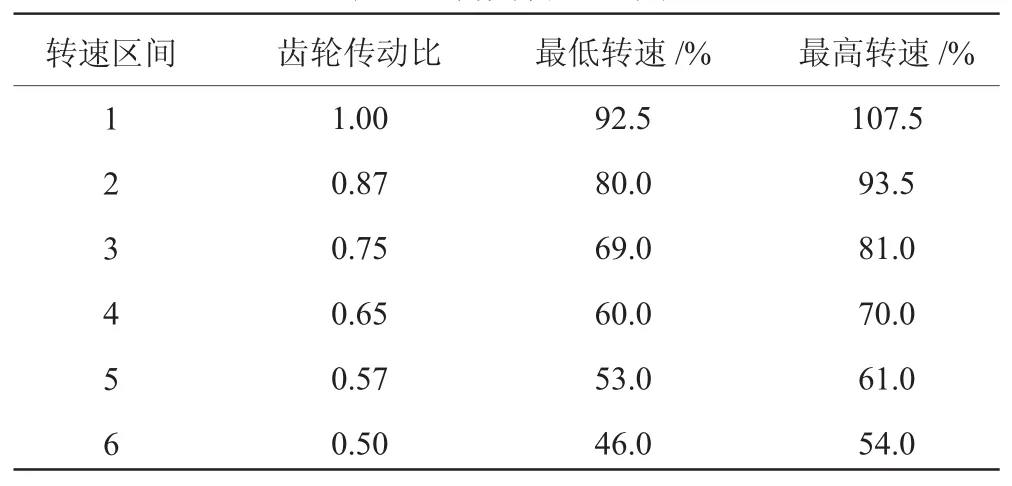
表1　旋翼转速范围

旋翼转速从1个转速区间变换到另1个区间的详细流程如图4所示。为了方便区分，将2台涡轴发动机定义为发动机#1和发动机#2，PT#1和PT#2分别为发动机#1和发动机#2的动力涡轮，流程如下：

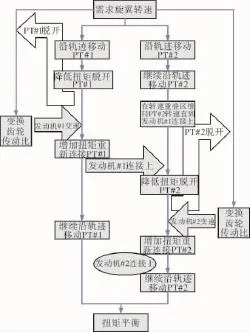
图4　扭矩序列转移控制方案流程

（1）保持PT#1的转速不变，通过离合器使得PT#1与旋翼脱开，则PT#1的输出功率降低，即PT#1的扭矩减小，当PT#1扭矩足够小时，通过变速器使其变速；

（2）与此同时由功率平衡控制器给定PT#2的扭矩，可知PT#2扭矩增大，且PT#2与旋翼连接并提供旋翼需求功率，将其按照设定的转速轨迹改变旋翼转速；

（3）当PT#2的转速到达转速区间临界值时，通过离合器使得PT#1与旋翼重新连接上，则PT#1的扭矩增大；

（4）与此同时通过离合器将PT#2与旋翼脱开，可知PT#2扭矩减小，当PT#2的扭矩足够小时，通过变速器使其变速，此时由PT#1与旋翼连接并提供旋翼需求功率，将其同样按照设定的转速轨迹改变旋翼转速。

只有PT#2的变速传动比与PT#1的变速传动比相同，变速之后的PT#1转速与PT#2在1个转速区间，PT#1才可以重新连接旋翼。如此重复上述操作，并按照表1的转速区间调节多级变速箱的齿轮传动比，即可实现旋翼转速6个区间范围46%～107.5%的变化。

3　变旋翼转速仿真实例

3.1数值模型仿真平台

基于直升机/涡轴发动机综合非线性系统实时仿真平台进行数字仿真验证，仿真平台结构详见文献［9］，其中直升机非线性、非定常实时模型采用黑鹰UH-60A直升机数据，包含主旋翼、机身、尾桨、平尾和垂尾等5个子模块，在此只用到直升机模型当中的旋翼模块做数字仿真验证。涡轴发动机非线性部件级模型采用T700发动机的数据建模。旋翼与发动机模型之间通过多级变速器与主减速器进行传动，多级变速器可以根据转速所在区间自动调节传动比。该综合仿真模型经过大量的仿真验证，具有可靠的置信度。

3.2转速控制器设计

在变旋翼转速过程中，涉及到旋翼扭矩的强扰动变化，而由于直升机与发动机之间的强耦合作用，发动机动力涡轮转速很容易受此强扰动变化影响，针对该问题，考虑采用由韩京清研究员提出的自抗扰技术设计控制器［11］。通过扩张状态观测器实时观测系统扰动状态量，及时将被控对象补偿成“二次积分型”。将旋翼扭矩扰动设计成前馈补偿器，可以在一定程度上改善直升机/发动机综合控制效果。该控制算法不仅在渐进稳定性方面已得到证明，而且已经在多个领域得到应用。线性矩阵不等式LMI适宜于求解存在不确定性的复杂多变量对象控制问题，可用于设计转速指令跟踪控制器。综上所述，在变旋翼转速过程中，采用鲁棒LMI+ADRC扭矩前馈的综合控制算法，可以快速地跟踪指令转速，有效的减少调节时间，减小超调量与下垂量，其结构如图5所示。文献［12］详细地给出了以2阶SISO发动机系统为对象LMI鲁棒控制器设计方法，文献［13］给出了ADRC控制器设计方法，在此不再叙述。

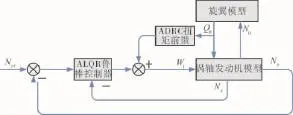
图5　LMI鲁棒控制器+ADRC扭矩前馈控制器结构

根据文献［14-15］提出的鲁棒控制设计方法，对于系统

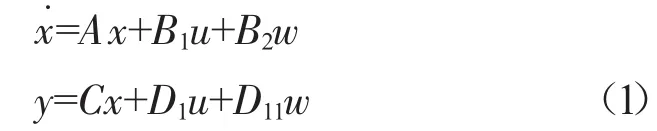
式中：x为系统状态；y为系统输出；u为控制量；w为系统扰动；A、B1、C、D1、B2、D11为适维矩阵。

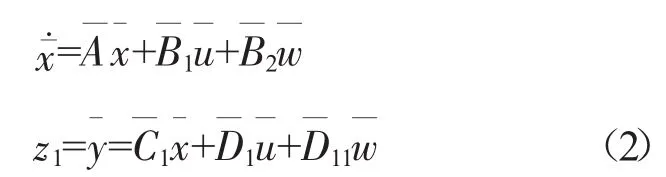
对于增广后的系统（2），可用H∞/H2等状态反馈设计方法求取状态调节器，使其满足，且二次型性能指标尽可能小。

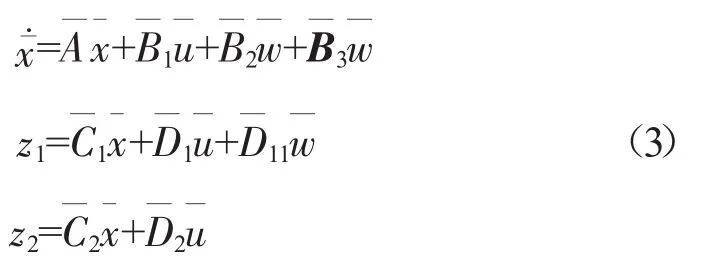
对于系统（3）和1个给定的标量γ1＞0，若以下优化问题

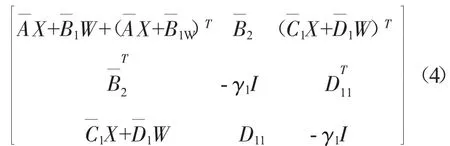
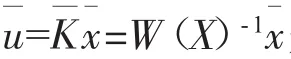
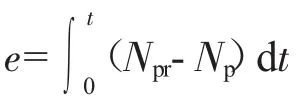
以直升机飞行高度H=0，Vx=Vy=0，Vz=0 m/s，在发动机状态Np=100%，Ng=88.6%的条件下设计控制器为例，式（1）中

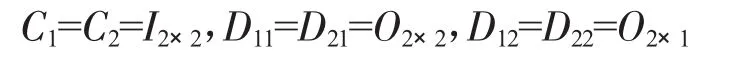
选取加权矩阵Q=［1111］，R=1，按照鲁棒控制器设计方法，得出 Ke=0.7257，Kx=［-2.6069 0.7030］。因此，基于LMI的鲁棒控制规律为u=Ke· e+Kx·x。

ADRC扭矩前馈控制器参数设计结果如下：

（1）微分观测器（TD）相关参数：过程响应快速性因子r0=0.75，仿真步长取h=0.05。

（2）扩张状态观测器（ESO）相关参数k1=50；k2=150；k3=200；非线性fal（·）的曲线方次因子mo1=0.5，mo2=0.25。

（3）非线性组合（NLSEF）相关参数：控制器增益l1=0.08；l2=0.08；非线性fal（·）的曲线方次因子α1= 0.5，α2=1.2；控制输入线性增益估计因子b0=26。

3.3仿真结果分析

在飞行包线内H=0 m，Vx=0 m/s处，将旋翼转速从转速区间1降低到转速区间2，即实现旋翼转速从107.5%到80%的变化，实现结果如图6所示。

从图6（a）中可见，在10s时PT#2与旋翼脱开，PT#2扭矩减小，PT#1扭矩增大，当PT#2扭矩足够小，在15s时开始变速，PT#2的输出轴转速瞬间NGB改变，同时PT#1带动旋翼从转速107.5%降低到92.5%。当PT#1的转速降低到93.5%，即在16.3s时，PT#1与旋翼脱开，PT#2与旋翼连接上，PT#1的扭矩减小，PT#2扭矩增大，当PT#1的扭矩足够小时，在20s时，PT#1变速，PT#1的输出轴转速瞬间改变，同时PT#2带动旋翼变化，旋翼转速从92.5%降低到80%，旋翼转速降低12.5%，在20.9s时，PT#1重新连接上旋翼，与PT#1一起共同平分旋翼需求功率。

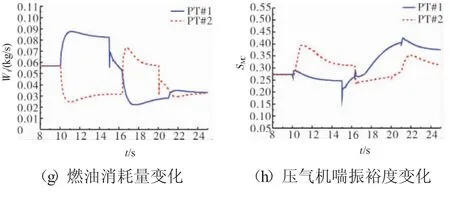
图6　在H=0 m，Vx=0 m/s处，旋翼转速从区间1降低到区间2的仿真曲线

在整个过程中旋翼转速降低了27.5%，且旋翼转速的变化平滑，花费时间为10.9s。在动力涡轮转速轨迹跟踪过程中，动力涡轮转速轨迹和发动机扭矩的变化范围之大，如此大的扰动对发动机动力涡轮转速影响强烈，图中结果显示动力涡轮转速下垂量为0.75%，超调量为0.4%，在发动机动力涡轮转速的允许范围之内。

采用串级PID综合控制算法，旋翼转速的仿真结果图6（b）所示。从图中可见，旋翼转速即动力涡轮转速转速下垂量为0.93%，超调量为1.21%，与采用串级PID综合控制算法相比，采用鲁棒LMI+ADRC扭矩前馈的综合控制算法得到的动力涡轮转速的下垂量与超调量更小，抗扰抑制作用更加明显，控制效果更加优越。

发动机以及旋翼扭矩值如图6（c）所示。从图中可见，旋翼转速的降低导致旋翼扭矩也降低，2台发动机的扭矩呈依次增减状态。动力涡轮转速PNP、燃气涡轮转速PNC、涡轮后温度T45、燃油消耗量Wf、压气机喘振裕度SMC变化情况分别如图6（d）、（e）、（f）、（g）、（h）所示。整个变旋翼转速控制过程中发动机不超转、不超温、不进喘，满足发动机控制系统要求。

在飞行包线内H=1000 m，Vx=20 m/s处，将旋翼转速从转速区间1降低到转速区间2，如图7所示。从图7（a）中可见，动力涡轮转速下垂量为0.2%，超调量为0.18%，在发动机动力涡轮转速的允许范围之内。采用串级PID综合控制算法，旋翼转速的仿真结果如图7（b）所示。从图中可见，旋翼转速下降时会产生剧烈振荡，且下垂量达到3.33%，采用鲁棒LMI+ADRC扭矩前馈的综合控制算法比采用串级PID综合控制算法，动力涡轮转速的下垂量更小、抗扰抑制控制效果更加明显。

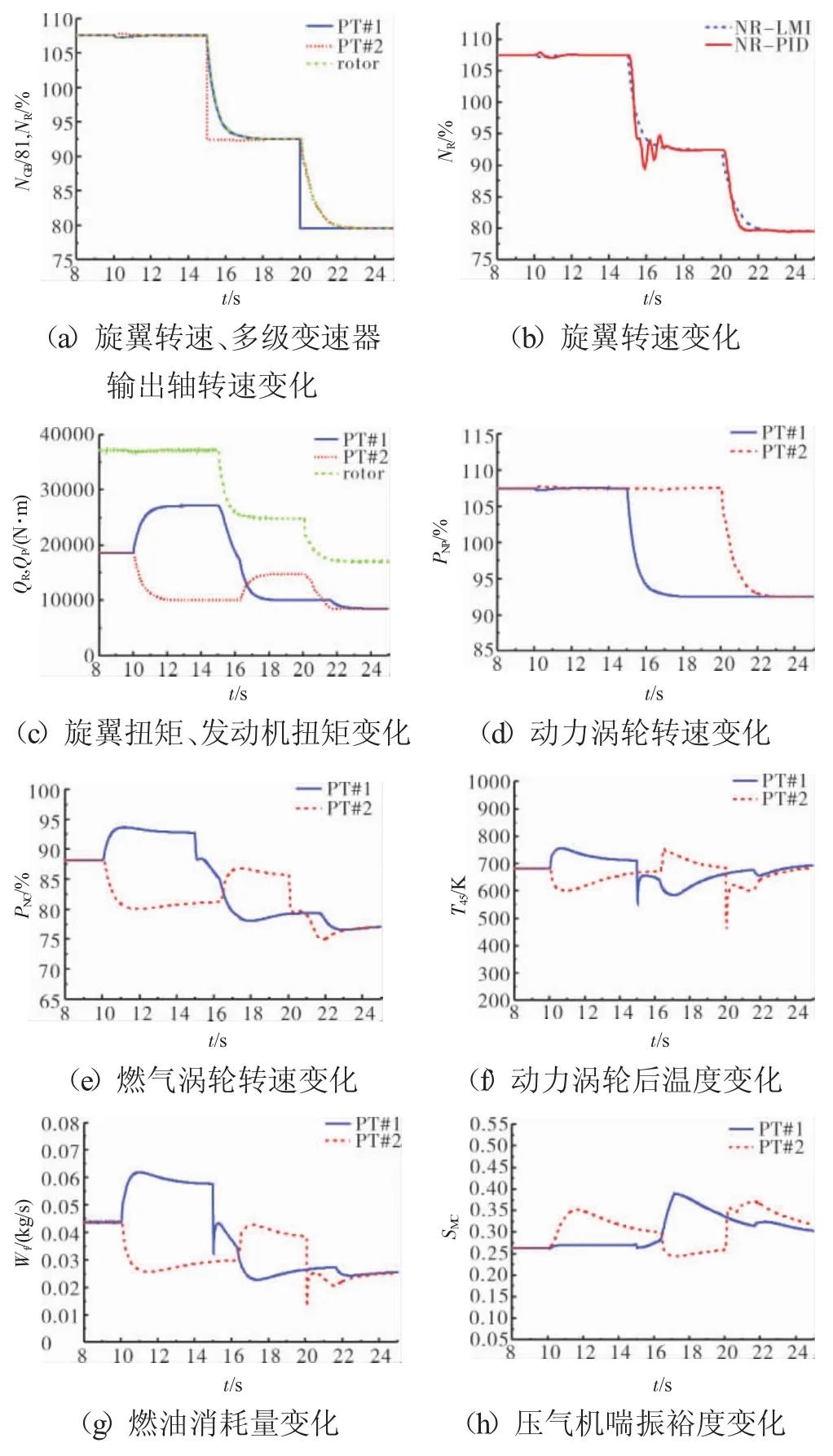
图7　在H=1000 m，Vx=20 m/s处，旋翼转速从区间1降低到区间2的仿真曲线

4　结论

针对直升机变旋翼转速实现问题，提出了1种扭矩序列转移方案。在该方案下，可以实现旋翼转速较大范围内的连续变化，且提供的旋翼需求功率连续不间断，在直升机/发动机综合数值模型平台下，对该方案进行了数字仿真，仿真结果表明，在转移过程中的扭矩强扰动变化对发动机动力涡轮转速的影响较小，旋翼转速可以实现较大范围内变化。

［1］Wei Guo，Horn J F.Rotor state feedback control for rotorcraft with variable rotor speed［R］.AIAA-2009-5797.

［2］Howlett J J，Morrison T，Zagaranski R D.Adaptive fuel control for helicopter application［J］.Journal of the American Helicopter Society，1984，29（4）：43-54.

［3］Takanori Iwata，Stephen M.Rock.Benefits of variable rotor speed in integrated helicopter/engine control［R］.AIAA-93-3851.

［4］Chen R T N.An exploratory investigation of the flight dynamics effects of rotor RPM variations and rotor state feedback in hover［R］. NASA-TM-1992-103968.

［5］Goi T，Kawakami K，Yamakawa E，et al.，Variable rotor speed transmission with high speed traction drive［R］.The American Helicopter Society 55th Annual Forum，Montreal，Canada，1999.

［6］张海波，姚文荣，王日先.直升机/发动机系统变旋翼转速串行优化方案［J］.航空动力学报，2010，25（10）：2363-2371. ZHANG Haibo，YAO Wenrong，WANG Rixian.Rotor speed changeable cascaded optimization method for helicopter/engine system［J］. Journal of Aerospace Power，2010，25（10）：2363-2371.（in Chinese）

［7］Bettner J L，Hawkins J M.High speed rotorcraft propulsion concepts to control power/speed characteristics［R］.AIAA-92-3367.

［8］Litt J S，Edwards J M，DeCastro J A.A sequential shifting algorithm for variable rotor speed control［R］.NASA-TM-2007-214842.

［9］姚文荣，孙健国.基于变旋翼转速的涡轴发动机优化控制［J］.航空动力学报，2007，22（9）：1573-1577. YAO Wenrong，SUN Jianguo.Optimization for turboshaft engines based on variable rotor speed［J］.Journal of Aerospace Power，2007，22（9）：1573-577.（in Chinese）

［10］Ai Xiaolan.Two speed transmission with smooth power shift：US，7044877［P］.2004-04-16.

［11］韩京清.自抗扰控制技术：估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2008：9. HAN Jingqing.Active disturbance rejection control technique：the technique for estimating and compensating the uncertainties［M］.Beijing：Defense Industry Press，2008：9.（in Chinese）

［12］张海波，孙立国，孙健国.直升机/涡轴发动机综合系统鲁棒抗扰控制设计［J］.航空学报，2010，31（5）：883-892. ZHANG Haibo，SUN Liguo，SUN Jianguo.Robust disturbance rejection control design for integrated helicopter system/turbo-shaft engine［J］.Acta Aeronautica et Astronautica Sinica，2010，31（5）：883-892.（in Chinese）

［13］张海波，孙健国，孙立国，一种新的涡轴发动机转速抗扰控制器设计及应用［J］.航空动力学报，2010，25（2）：471-476. ZHANG Haibo，SUN Jianguo，SUN Liguo.The design and application ofa newdisturbance rejection rotor speed control method for turbo-shaft engines［J］.Journal of Aerospace Power，2010，25（2）：471-476.（in Chinese）

［14］俞立.鲁棒控制—线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002. YU Li.Robust Linear Matrix Inequality method［M］.Beijing：Tsinghua University Press，2002.（in Chinese）

［15］Apkarian P，Tuan H D ，Bernussou J，et al.Continuous-time analysis，eigenstructure assignment and H2 synthesis with enhanced Linear Matrix Inequality（LMI）characterizations［J］.IEEE Transactions on Automatic Control，2001，46（12）：1941-1946.

（编辑：张宝玲）

Research on Variable Rotor Speed Control Based on Integrated Helicopter/Engine Model

CHEN Guo-qiang，YANG Juan
（AVIC Aeroengine Control Research Institute，Wuxi Jiangsu 214063）

A sequential shifting algorithm was proposed for changing the helicopter rotor's speed in a large variation and providing continuous output power to the rotor.Two turbo-shaft engines and two multi-speed gearboxes coordinate with the rotor that facilitate a wide rotor speed variation and provide continuous torque to the rotor.Aiming at the problem of turbo-shaft engine's torque disturbance，the robust ALQR controller combined with ADRC torque feed forward compensation was designed in the process of shifting.Some numerical simulations are carried out to verify the feasibility of the shifting algorithm based on the integrated helicopter/engine model.The simulation results show that the torque disturbance has little influence on engine power turbine speed in the process of torque shifting，and the rotor speed can perform rapid and smooth changes at larger range.

variable rotor speed；torque sequential shift；multi-speed gearboxes；integrated helicopter/engine model；aeroengine

V 233.7

Adoi：10.13477/j.cnki.aeroengine.2016.05.003

2016-03-16基金项目：国家重大基础研究项目资助

陈国强（1986），男，硕士，主要从事直升机/发动机建模及控制优化研究工作；E-mail：nuaachen2005@163.com。

引用格式：陈国强，杨娟.基于直升机/发动机综合模型的变旋翼转速控制研究［J］.航空发动机，2016，42（5）：14-20.CHENGuoqiang，YANGJuan.Research onvariablerotorspeedcontrolbasedonintegratedhelicopter/enginemode［J］.Aeroengine，2016，42（5）：14-20.