基于随机几何的大规模无线传感器网络点平均干扰研究*

诸浩富　毛剑琳　王昌征　付丽霞　郭　宁

(昆明理工大学信息工程与自动化学院　昆明　650500)



基于随机几何的大规模无线传感器网络点平均干扰研究*

诸浩富毛剑琳王昌征付丽霞郭宁

(昆明理工大学信息工程与自动化学院昆明650500)

针对无线传感器网络中的干扰问题,从节点随机分布出发,分别对在单个正六边形和相邻两个正六边形内的节点随机分布进行网络点平均干扰和网络加权点平均干扰的研究,推导和计算网络点平均干扰函数;同时考虑节点之间的通信概率,提出网络加权点平均干扰的计算方法,并利用蒙特卡洛法对这两种干扰计算方法进行仿真,获得边长与点平均干扰的函数关系式。仿真结果表明,网络点平均干扰函数与理论计算公式较为吻合,所提出的网络加权点平均干扰函数更符合实际的网络干扰情况。两种干扰计算方法为估算大规模网络干扰提供了理论和现实依据。

干扰; 无线传感器网络; 通信概率; 蒙特卡洛

Class NumberTP212.91

1　引言

无线传感器网络(Wireless Sensor Networks,WSNs)已经被应用在许多关键领域,如应急管理系统、民用基础设施的监测、医疗卫生保健等[1]。因而其网络性能越来越受到人们的关注,是当前信息领域研究和开发的一个热点。

网络干扰问题是WSNs中十分重要的且亟待解决的问题,而传感器节点的分布对干扰有着很大的影响[2]。目前,多数研究节点分布情况都是只研究其均值和方差[3]。而且由此来研究网络的干扰时,往往是以几何圆、几何矩形为基础研究节点播撒的情况。梁栋等[4]提出了一种基于多项式窗函数模型的干扰自优化方案;Yu等[5]设定网络的干扰范围大于其通信范围,其对点干扰的定义也扩展到在干扰范围内的所有节点数量,网络的干扰则为节点的最大干扰值。同时,现有的研究网络干扰的情况往往未考虑通信概率的问题,使得理论干扰与实际干扰存在较大的偏差。此外在WSNs中,当规模较大时,某些关键性能指标可以利用随机特征对其进行量化处理[6],因而可将网络干扰与节点播撒区域的边长相联系。

Zhuan等[2,7～8]基于随机几何方法,针对节点距离关系和位置关系,对其在菱形、单个正六边形、相邻两个正六边形等情况进行节点随机分布的研究,获得其距离分布函数,但未对网络的其他性能展开研究。本文在节点随机距离分布函数的基础上,突破几何圆形播撒区域,选用能使得网络覆盖面积更大的正六边形为研究对象,以节点随机分布为研究前提,推导并验证一种网络点平均干扰的计算方法;同时,结合实际考虑节点之间的通信概率,给出了一种新的网络加权点平均干扰的计算方法,并采用蒙特卡洛(Monte Carlo)法获得干扰与边长的近似拟合函数。

2　大规模无线传感器网络干扰问题的描述

干扰指标一直是WSNs的重要性能指标之一。而以往的相关文献都是停留在研究某一固定区域内的网络干扰。随着大规模WSNs的不断推广,对节点播撒区域的大小与网络干扰的关系进行研究就显得很有必要。

针对此类情况,本文的研究设定如下:考虑节点分布区域边界为正六边形,节点随机分布且节点数目足够多。若区域为单个正六边形,则节点可彼此通信,这种通信方式属于同一区域内的通信。若区域为相邻两个正六边形,则节点只能与另一个正六边形内的节点进行通信。此种通信方式适用于大规模网络的远距离通信,属于不同区域的通信。

3　网络干扰的推导

在无线传感器网络中,其节点的发射功率、链路增益函数以及路径损耗函数对于网络干扰有着极大的影响[6],因此对于网络的干扰问题综合起来考虑就显得很有必要。本文选用Martin等[6]提出的网络干扰I的数学模型:

I=∑P·H(d)·L(d)

(1)

其中P表示节点的最优发射功率;H(d)表示以节点的链路增益为自变量的函数;L(d)表示路径损耗函数;d表示节点之间的距离。

对于式(1)中的链路增益函数和路径损耗函数,可如下表示[9～10]:

(2)

(3)

其中α表示路径损耗(衰减)指数,一般取2～6。Maciej和Heinzelman等[10～11]指出,自由空间模型时,α=2,多路径衰减模型时,α=4。

为得到节点的最优发射功率,选用文献[12]提出的数学模型,如下:

(4)

其中Pr表示接收端天线接收功率;Pt表示发送端天线发射功率;Rth表示功率门限阈值(假设接收节点想要正确检测并解码信号的功率门限阈值为Rth,只有当接收信号的强度大于Rth时才可成功接收信号);考虑到信道的衰减特性,故对所求的最优发射功率乘以一个大于等于1系数C,以此使信号在信道中能够得到可靠的传输。

Rodoaplu等[13]指出,通信模块共有发送、接收、空闲、睡眠四种不同的状态,且这四种状态的功率比约为2000:400:400:1,即有Pt/Pr=5。那么节点的最优发射功率为

Popt=5CRth

(5)

根据式(1)～式(5),分别对单个正六边形内的网络干扰Is和相邻两个正六边形内的网络干扰Id进行考虑,其网络干扰的数学模型如下:

(6)

(7)

其中Pij表示节点i到j的最优发射功率;H(dij)表示以节点i到j的链路增益为自变量的函数;L(dij)表示路径损耗函数;dij表示节点i到j的距离;符号“[]”表示取整。

3.1网络点平均干扰的推导

以节点通信距离d为研究对象,根据数理统计理论得到网络点平均能耗。Zhuang等[7～8]研究表明,在节点随机分布的情况下,若正六边形播撒区域的边界为L,则节点间距离的期望如下:

Es(Ld)=LEs(d)=0.8262589495L

(8)

Ed(Ld)=LEd(d)=1.8564318344L

(9)

式中Es(Ld)表示边长为L的单个正六边形内节点之间的距离为d时的期望;Ed(Ld)表示边长为L的相邻两个正六边形内节点之间的距离为d时的期望。

利用其距离期望,结合式(2)～式(9),分别可得在单个正六边形区域和相邻两个正六边形区域内的网络点平均干扰Is1和Id1,其表达式如下:

(10)

(11)

式(10)和(11)即为根据距离期望求得的网络点平均干扰。

为方便计算和仿真,分别对式(10)和式(11)两边取以10为底的对数,得到如下表达式:

fIs1=logIs1=-2αlog(Es(Ld))

+log(7.75×10-13)+logPopt

(12)

fId1=logId1=-2αlog(Ed(Ld))

+log(7.75×10-13)+logPopt

(13)

其中“log”表示以10为底的对数。

3.2网络加权点平均干扰的推导

3.2.1节点通信概率

由于无线传感器网络的实际应用中,节点并非以同一概率与周围节点进行通信,特别是在多跳传输的情况下,节点往往需要在通信距离和能量消耗间进行折中来选择下一跳通信节点。考虑到这一点,本文利用节点的距离分布,给出随机分布的大规模网络中任意2个节点的通信概率如下:

假设随机分布n个节点,在这n个节点中随机取2个节点构成一条通信路径,则在整个网络中,对于单个正六边形,存在有条通信路径;对于相邻两个正六边形,因其属于不同区域之间的通信,故存在有条通信路径。将这些通信路径按距离大小列出其频率分布表,此时所得的频率即为在该距离下的通信概率。其中符号“[]”表示取整。单个正六边形和相邻两个正六边形内的通信概率用数学公式描述如下:

(14)

(15)

其中,M表示在单个正六边形内,节点i～j的距离dij出现的次数;N表示在相邻两个正六边形内,节点i到j的距离dij出现的次数。

在式(14)和(15)的定义下,节点倾向于选择通信距离适中的邻节点进行通信,而以较低的概率选择那些距离过远或过近的邻节点,这符合网络节点多跳通信时对通信距离和能量消耗折中的原则。

3.2.2网络加权点平均干扰

为研究加权计算的网络点平均干扰函数,本文引入随机变量为自变量构成的函数的分布概率的定义及其数学期望的定义[14]。定义如下:

定义1设D为随机变量,其可能取值为di,i=1,2,3…,且di所对应的概率为pi,f(d)为连续函数,则F=f(D)为随机变量D的函数,也是随机变量。同时,F的概率分布如下:

f(D)f(d1)f(d2)…f(dn)Pp1p2…pn

其数学期望定义如下:

(16)

因此,根据加权算术平均值理论,结合通信概率和式(16),分别针对单个正六边形区域和相邻两个正六边形区域定义网络加权点平均干扰Is2和Id2,如下:

(17)

(18)

式(17)和式(18)即为根据加权算术平均值理论求得的网络加权点平均干扰。

为方便计算和仿真,分别对式(17)和式(18)两边取以10为底的对数,得到如下表达式:

fIs2=logIs2

(19)fId2=logId2

(20)

其中“log”表示以10为底的对数。

4　仿真验证

4.1仿真设置

本文采用Matlab R2012a为仿真计算平台,假设各个传感器节点处于相互通信状态,对网络点平均干扰进行仿真验证。表1给出了网络干扰的仿真参数。

4.2网络点平均干扰验证

根据式(12)和式(13),利用Matlab对网络点平均能耗进行仿真。图1给出了单个正六边形内网络点平均干扰函数关系图;图2给出了相邻两个正六边形内网络点平均干扰函数关系图。在图1和图2中,给出了理论网络点平均干扰函数的部分坐标点,其中横坐标X表示边长(m),纵坐标Y表示网络点平均干扰(DB)。

表1　仿真参数设置

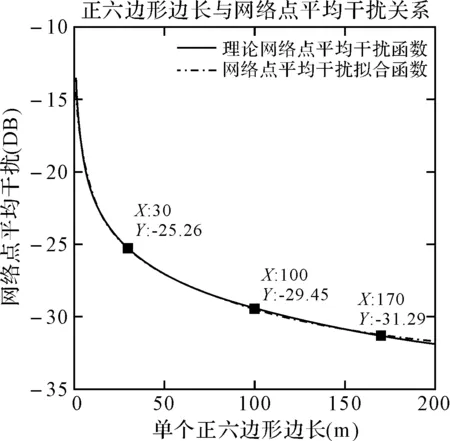
图1　单个正六边形内网络点平均干扰函数关系图

由图1和图2可以明显看出,无论是在单个正六边形内还是在相邻两个正六边形内,仿真获得的网络点平均干扰函数与理论推导的网络点平均干扰函数较为吻合。这就证明本文推导的网络点平均干扰函数是正确的。同时,从图1和图2中可以看到,随着边长的不断增加,网络点平均干扰会呈现几何倍数的减小。这是因为当节点数目一定时,节点撒播区域的增加,使得节点之间的距离增加,节点布局变得稀疏,从而导致网络点平均干扰的减小。而且,由图1和图2对比发现,在边长相同的情况下,相邻两个正六边形(即不同区域的通信)内的网络点平均干扰,远远小于单个正六边形(同一区域的通信)内的网络点平均干扰。这一仿真结果表明,理论的网络点平均干扰与实际的网络点平均干扰情况是一致的。可见本文推导的理论网络点平均干扰函数是有理论和实际意义的。

图2　相邻两个正六边形内网络点平均干扰函数关系图

4.3网络加权点平均干扰验证

根据式(19)和式(20),利用Matlab对网络加权点平均干扰进行仿真。表2给出了单个正六边形和相邻两个正六边形内根据加权算术平均理论获得的网络加权点平均干扰的仿真拟合函数,其中L为正六边形边长,f为网络加权点平均干扰;图3给出了单个正六边形内加权计算的网络加权点平均干扰函数图;图4给出了相邻两个正六边形内加权计算的网络加权点平均干扰函数图。在图3和图4中,给出了网络加权点平均干扰函数的部分坐标点,其中横坐标X表示边长(m),纵坐标Y表示网络加权点平均干扰(DB)。

表2　加权计算的网络点平均干扰拟合函数

由图3和图4可以明显看出,随着边长的不断增加,网络点平均干扰会呈现几何倍数的减小。而且,在边长相同的情况下,相邻两个正六边形内的网络加权点平均干扰,远远小于单个正六边形内的网络加权点平均干扰。这一仿真结果表明,利用加权理论获得的网络加权点平均干扰与实际的网络点平均干扰情况是一致的。由图3和图1、图4和图2对比发现,加权计算的网络点平均干扰大于理论的网络点平均干扰。这是因为考虑了通信概率,使得网络点平均干扰更加符合实际情况。同时,在表2中给出了网络加权点平均干扰函数,这就为以后估算网络的总体干扰提供了理论依据和计算方法。

图3　单个正六边形内网络加权点平均干扰函数关系图

图4　相邻两个正六边形内网络加权点平均干扰函数关系图

5　结语

本论文在研究了单个正六边形和相邻两个正六边形内网络点平均干扰与正六边形边长的关系。本文先在Zhuang和Pan的距离分布函数的基础上利用蒙特卡洛法推导网络点平均干扰函数,利用Matlab仿真获得网络加权点平均干扰函数。仿真结果表明,本文推导的理论网络点平均干扰函数是正确有效的;提出的利用加权理论获得网络加权点平均干扰更贴近实际情况,在实际应用中,可以利用此函数对网络的总体干扰进行估计。在后继的工作中,将通过对大规模无线传感器网络节点的距离分布及其干扰的研究,进一步研究大规模无线传感器网络的容量等问题,从而为提高大规模无线传感器网络的性能等提供科学理论和现实依据。

[1] Xiangmao Chang, Jun Huang, Shucheng Liu, et al. Accuracy-Aware Interference Modeling and Measurement in Wireless Sensor Networks[J]. IEEE Transactions on Mobile Computing,2016,15(2):278-291.

[2] Yanyan Zhuang, Jianping Pan. A Geometrical Probability Approach to Location-Critical Network Performance Metrics[C]//Proceedings IEEE INFORCOM,2012:1817-1825.

[3] S. Srinivasa, M. Haenggi. Modeling interference in finite uniformly random networks[C]//Proc. International Workshop on Information Theory for Sensor Networks (WITS’07),2007:1-12.

[4] 梁栋,覃武凌,刘书龙,等.基于多项式窗函数模型的WLAN干扰自优化方法[J].北京邮电大学学报,2014,37(4):6-9.

LIANG Dong, QIN Wulin, LIU Shulong, et al. Self-Optimization Scheme Aimed to WLAN Interference Based on Polynomial Window Function Model[J]. Journal of Beijing University of Posts and Telecommunications,2014,37(4):6-9.

[5] Xiang Yu, Xinming Zhang, Can Que, et al. A practical low interference topology control for mobile ad hoc networks[C]//Sixth International Conference on Networking (ICN’07),2007:23-23.

[6] Martin Haenggi, Jeffrey G. Andrews, Francois Baccelli, et al. Stochastic Geometry and Random Graphs for the Analysis and Design of Wireless Networks[J]. IEEE Journal on Selected Areas in Communications,2009,27(7):1029-1046.

[7] Yanyan Zhuang, Jianping Pan. Random distances associated with rhombuses[R]. ArXiv Technical Report, arXiv: 1106.1257,2011.

[8] Yanyan Zhuang, Jianping Pan. Random Distances Associated with Hexagons[R]. ArXiv Technical Report, arXiv: 1106.2200,2011.

[9] 郑耿忠,刘三阳,齐小刚.基于非合作博弈的无线传感器网络功率控制研究[J].控制与决策,2011,26(7):1014-1018.

ZHENG Gengzhong, LIU Sanyang, QI Xiaogang. Study on power control of wireless sensor networks based on non-cooperative game[J]. Control and Decision,2011,26(7):1014-1018.

[10] Maciej Zawodniok, Sarangapani Jagannathan. A Distributed Power Control MAC Protocol for Wireless Ad Hoc Networks[C]//Wireless Communications and Networking Conference,2004,3:1915-1920.

[11] Heinzelman W R, Balakrishnan A C H. Energy-efficient communication Protocol for Wireless Microsensor Networks[C]//Proceeding of HICSS’00, Hawaii, USA,2000,2:4-7.

[12] Pelin C. Nar, Erdal Cayirci. PCSMAC: A Power Controlled Sensor-MAC Protocol for Wireless Sensor Networks[C]//Proceeedings of the Second European Workshop on Wireless Sensor Networks,2005:81-92.

[13] Rodoaplu V, Meng T H. Minimum Eneigy Mobile Wireless Networks[J]. IEEE Journal on Selected Areas in Communications,2006,17(8):1333-1334.

[14] 戴琳.概率论与数理统计[M].北京:高等教育出版社,2009:35-36.

DAI Lin. Probability theory and mathematical statistics[M]. Beijing: Higher Education Press,2009:35-36.

Point Average Interference in Large-Scale Wireless Sensor Networks Based on Stochastic Geometry

ZHU HaofuMAO JianlinWANG ChangzhengFU LixiaGUO Ning

(Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming650500)

For the interference problem in WSNs,this article embarks from the random distribution of sensor nodes, and researches the interference in a single regular hexagon and two adjacent regular hexagon. Finally, point average interference function is derived and calculated. Meanwhile, considering the communication probability of nodes, weighted point average interference function is put forward. And the two calculation methods of interference are simulated by using Monte Carlo method. The simulation results show that the point average interference simulation function is consistent with theoretical calculation, and weighted point average interference function matches the actual network better. These two calculation methods of interference for estimating the large-scale network interference provide theoretical and practical basis.

interference, wireless sensor networks, communication probability, Monete Calo

2016年3月7日,

2016年4月26日

国家自然科学基金项目“异构无线传感执行器不对称竞争接入控制算法”(编号:61163051)资助。

诸浩富,男,硕士研究生,研究方向:无线传感器网络。毛剑琳,女,教授,研究方向:传感器网络优化与控制。王昌征,男,硕士研究生,研究方向:传感器网络覆盖。付丽霞,女,讲师,研究方向:计算机控制、嵌入式系统。郭宁,女,实验师,研究方向:无线传感器网络、随机过程。

TP212.91DOI:10.3969/j.issn.1672-9722.2016.09.025