基于坐标变换的矩阵函数计算*

汪海锐　林明胜　谢　宇

(海军蚌埠士官学校　蚌埠　233012)



基于坐标变换的矩阵函数计算*

汪海锐林明胜谢宇

(海军蚌埠士官学校蚌埠233012)

根据矩阵函数的理论,调整了矩阵函数计算过程中的步骤及方法,对通过最小多项式求矩阵函数的算法,采用基坐标变换的形式进行了调整,通过换元思想,使计算过程得以简化,中间计算结果能够复用。调整后的计算过程,更不容易出错,并通过示例说明了计算步骤。

矩阵函数; 最小多项式; 矩阵; 待定系数

Class NumberTP301

1　常用矩阵函数计算方法

对于矩阵函数[1]而言,其主要计算思路是利用矩阵函数的性质[2]进行的,一般采用递推公式计算法或相似标准形计算法来完成,常用矩阵函数的计算方法[3～8]主要利用方阵幂级数来进行定义矩阵函数,并根据收敛性来进行求取其矩阵函数,或利用最小多项式计算的方法,或利用矩阵函数的谱分解与有限表示方法来进行求取其矩阵函数的结果。

相对利用幂级数进行求取矩阵函数[9]而采用Jordan矩阵求取方法[10],最小多项式的计算方法相对简单,其计算量略小,在手工计算及程序设计辅助计算过程中,更容易为人接受并采用。

为此,对矩阵函数的最小多项式的计算方法进行了整理,其原理与基变换方法求多项式泰勒级数公式一样[11],本文通过调整其计算步骤,简化其计算过程,使得采用手工计算时,更不容易出错,在程序设计辅助计算时,使程序设计思路更加清晰。

2　待定系数法进行矩阵函数的计算

采用待定系数法进行函数的计算,其依据为如下定理。

定理[7]:设n阶方阵A的最小多项式为m次多项式:

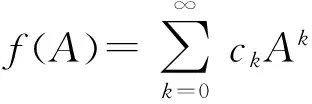
系数a0,a1,a2,…,am-1满足下列方程组:

在具体计算过程中,求解其方程而得到各系数,再代入

f(A)=a0E+a1A+a2A2+…+am-1Am-1

得到最终矩阵函数的结果。

考虑到解以上方程组的实质是进行基坐标的变换,因此,对上述方程的求解过程进行调整,利用基变换的过渡矩阵来求取矩阵函数[11～12],具体示例如下。

3　调整后矩阵函数计算方法

已知:矩阵A;求解:矩阵函数f(A)。

其主要计算步骤如下:

1) 求解矩阵A的最小多项式φ(λ)=(λ-λ1)n1(λ-λ2)n2…(λ-λs)ns;

2) 根据最小多项式的阶次确定出等效的m-1次多项式:

f(A)=c0E+c1A+c2A2+…+cm-1Am-1

其中,系数c0,c1,…,cm-1均为待确定的值。

3) 通过基变换求取其结果:

f(A)=c0E+c1A+c2A2+…+cm-1Am-1

=(c0c1c2…cm-1)(EAA2…Am-1)T

将求解系数的方程组写成矩阵形式,可以得到:

由于其变换矩阵一定可逆,故此可得到其系数:

4) 求解矩阵函数f(A):

5) 在计算过程中,计算矩阵函数f(A)时,优先对数字矩阵进行计算,以此保证计算过程中的简洁性,使得计算过程不易出错。由于在计算过程中,优先对数字矩阵进行了计算,使得当矩阵函数中加入参数时,只需要更改对应的坐标即可,使得计算量能够大大地减小。

4　结语

在矩阵函数的计算过程中,采用待定系数法时,结合基坐标变换,使得整个计算过程具有更高的复用性,其计算结果可以在计算不同的矩阵函数中重复使用,而且采用基于坐标的待定系数的矩阵函数计算方法,其计算步骤更加清晰,更不容易出错。

[1] 方保镕,周继东,李医民.矩阵论[M].北京:清华大学出版社,2004.

FANG Baorong, ZHOU Jidong, LI Yiming. Matrix Theory[M]. Beijing: Tsinghua University Press,2004.

[2] 吴世轩,杜红霞.矩阵函数的性质[J].大学数学,2008,24(2):118-120.WU Shigan, DU Hongxia. The Property of Matrix Function[J]. College Mathematic,2008,24(2):118-120.

[3] 夏丹丹,江翠.关于矩阵函数的解法探讨[J].高等函数学报(自然科学版),2011,24(3):58-59.

XIA Dandan, JIANG Cui. On the solution of matrix function[J]. Journal of Higher Correspondence Education(Natural Sciences),2011,24(3):58-59.

[4] 黄承绪.矩阵指数函数的一些性质[J].武汉理工大学学报:交通科学与工程版,2001,25(2):147-149.HUANG Chengxu. Some Properties of Matrix Exponentials[J]. Journal of Wuhan University of technology(Transportation Science & Engineering),2001,25(2):147-149.

[5] 戴中林.矩阵函数f(A)的计算方法[J].大学数学,2012,28(1):144-150.DAI Zhonglin. Computational Method of Matrix Function f(A)[J]. College Mathematics,2012,28(1):144-150.

[6] 张俊祖,姜根明,冯复科.矩阵指数函数的一种计算[J].长安大学学报:自然科学版,2006,26(1):108-110.

ZHANG Junzu, JIANG Genming, FENG Fuke. A Computation Method od Matrix Exponent Function[J]. Journal of Chang’an University(Natural Science Edition),2006,26(1):108-110.

[7] 罗家洪,方卫东.矩阵分析引论[M].第四版.广州:华南理工大学出版社,2006.

LUO Jiahong, FANG Weidong. Introduction to matrix analysis[M]. the 4thEdition. Guangzhou: South China University of Technology Press,2006.

[8] 马翠云.矩阵函数的两种计算方法[J].周口师范学院学报,2007,24(2):34-36.

MA Cuiyun. Two computation methods of matrix function[J]. Journal of ZhouKou Normal University,2007,24(2):34-36.

[9] 杨明,刘先忠.矩阵论[M].第二版.武汉:华中科技大学出版社,2005.

YANG Ming, LIU Xianzhong. Matrix theory[M]. the 2ndEdition. Wuhan: Huazhong University of Science and Technology Press,2005.

[10] 李新,何传江.矩阵理论及其应用[M].重庆:重庆大学出版社,2005.LI Xin, HE Chuanjiang. Matrix theory and its applications[M]. Chongqing: Chongqing University Press,2005.

[11] 冯其明.用基变换方法求多项式的泰勒公式[J].无锡商业职业技术学院学报,2003,3(2):71-72.

FENG Qiming. Finding Taylor Formula of Multinomial with Radix Alternating Method[J]. Journal of Wuxi Vocational Institute of Commercial Technology,2003,3(2):71-72.

[12] 包健.基变换的过渡矩阵的求法[J].安庆师范学院学报:自然科学版,2004,10(4):78-81.

BAO Jian. Some Methods on Determining Transition Matrix in Transformation of Basic[J]. Journal of Anqing Teachers College(Natural Science Edition),2004,10(4):78-81.

Matrix Function Calculation Based on Frame Conversion

WANG HairuiLIN MingshengXIE Yu

(Bengbu Navy Petty Officer Academy, Bengbu233012)

Based on matrix function theory, steps and method in matrix function calculation are changed, the form of base frame conversion is used to change matrix function extracting which based on minimal polynomial algorithm. With the idea of changing variables, calculative process is simplified, intermediate computational results can be reutilized, the changed calculative process is less error-prone. Computation steps are introduced through demonstration.

matrix function, minimal polynomial, matrix, undetermined coefficient

2016年3月18日,

2016年4月25日

汪海锐,男,硕士研究生,助教,研究方向:通信与信息系统。林明胜,男,讲师,研究方向:无线通信。谢宇,男,硕士研究生,助教,研究方向:雷达技术。

TP301DOI:10.3969/j.issn.1672-9722.2016.09.010