基于灰色关联-集对分析的绿色建筑供应商选择

杨斯玲，蒋根谋

（华东交通大学　土木建筑学院，江西　南昌　330013）



基于灰色关联-集对分析的绿色建筑供应商选择

杨斯玲，蒋根谋

（华东交通大学土木建筑学院，江西南昌330013）

针对绿色建筑供应商选择中存在的多属性、不确定性等问题，在已有研究的基础上，围绕绿色建筑供应商的特点，从建筑产品优势、企业运营管理、合作潜力、绿色管理四个方面构建了供应商选择综合评价系统。基于集对分析理论，将确定性与不确定性因素相结合，建立评价集与指标集的集对；结合灰色关联理论，分别对其差异度与同一度、差异度与对立度之间的关联度进行量化分析；采用熵权法确定评价指标的权重，通过构造正、反同一度矩阵，选择最优供应商。最后，以实例验证了该方法用于绿色建筑供应商选择评价的适用性。

绿色建筑；供应商选择；灰色关联度；集对分析；熵权

1　引言

面对世界范围的能源危机和环境危机，保护生态环境、开发绿色产品、加快绿色建筑的发展已经成为社会和建筑行业的共识，绿色建筑已成为建筑行业可持续发展的总趋势。绿色建筑的开发和利用不是某一主体单独的行为，而是需要在供应链管理模式下通过各参与主体协同运作才能实现。绿色供应链管理作为一种全过程的环境管理模式，为绿色建筑的开发和利用提供了一种好的实施途径。绿色供应链在建筑行业的推广有利于改善建筑业高能耗、高污染的问题，也有利于推动绿色建筑的实现。选择合理的供应商是保证绿色建筑供应链运行的重要环节之一，因为处于绿色建筑供应链上游的供应商，其在保护环境和节约资源方面的作用能够通过供应链传递到下游的各个环节，从而在实施绿色供应链管理时发挥关键性的作用，实现建筑的绿色化［1-2］。在供应商评价和选择问题研究中，常用的方法有TOPSIS法、灰色关联分析法、理想点法、神经网络法等，如R. J.Kuo将人工神经网络（ANN）和多属性决策分析（MADA）方法相结合建立了ANN-MADA评价模型，对绿色供应商进行选择［3］。Seyed Hamid Hashemi提出在绿色供应商选择过程中考虑碳管理模式，利用改进的灰色关联分析法进行选择［4］。彭频提出在Partnering模式下，用基于熵权的TOPSIS法进行建筑供应商选择［5］。吴立云将熵理论和粗糙集结合，基于均衡接近度对绿色供应商进行灰色综合评价［6］。杨耀红研究了多目标智能加权灰靶决策在绿色供应链供应商选择中的应用［7］。颜波提出了基于超效率DEA模型的绿色供应链环境下供应商评价与选择方法［8］。贾安超将BP神经网络和粗糙集理论相结合，构建了绿色供应商选择模型［9］。可见，绿色建筑供应商选择评价是一个多属性决策问题，以往的多属性决策多从贴近度分析问题，实际上只考虑了评价对象的同一度，不够全面［10-11］。而采用集对分析能较好地解决这个问题，更加全面地分析事物特征。因此，本文将集对分析理论用于绿色建筑供应商选择评价，为了统筹考虑同、异、反三种特性，将灰色关联分析应用在衡量因素间关联程度分析中，量化两比较系统之间的关系，可以有效地判断评价对象与比较对象的影响程度［12］。此外，为了避免以往主观确定权重的随意性，采用熵权法确定评价指标权重，使评价结果更为客观、全面，为绿色建筑供应商的选择提供一种可行方法。

2　构建供应商选择综合评价指标体系

绿色建筑供应商的选择本质上是一个多属性决策问题，由于对绿色建筑供应商进行选择时涉及的评价指标有很多，包括技术、经济、社会和环境等多方面的因素。构建完善合理的指标体系是对绿色建筑供应商进行选择的核心问题。目前国内外针对绿色建筑供应商的研究较少，为了提取绿色建筑供应商的评价指标，本文一方面借鉴建筑业供应链管理中供应商选择的标准，另一方面借鉴的是已有的绿色供应链管理中供应商的选择，在分析绿色建筑供应商及绿色供应链特点的基础上，进行归类和融合，初步确定绿色建筑供应商选择可以从建筑产品优势、企业的运营管理、供应商合作潜力、绿色管理水平4个方面考虑。其中，建筑产品的优势主要包括建筑产品价格、建筑产品质量以及环保性能等；企业内部的运营管理则是从企业财务能力、信息化程度和物流水平（供货是否及时、仓储运输是否可靠）三个方面衡量；供应商合作潜力主要指企业文化兼容性、长期合作意向、高层领导支持、应急需求反应能力等因素；绿色管理主要从环境认证体系、产品绿色设计、绿色采购、绿色施工、绿色运营维护和绿色回收再利用等方面考察［13-14］。

3　灰色关联度-集对分析理论

3.1集对分析理论

1989年，中国学者赵克勤提出集对分析方法，其核心思想是运用对立统一的辨证观点，将确定性与不确定性相结合，从同、异、反三个方面综合、系统地分析集成问题。集对是将具有一定关系的两个集合组成对子，将其看成系统分析的整体。对于任意两个给定的集合A和B，可组成集对为H=（A，B），为将两集合的确定性与不确定性联系起来，采用表达式见式（1）［15］：

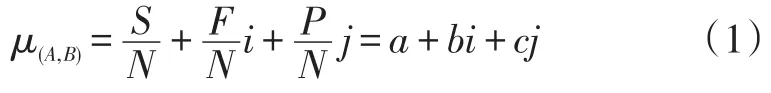
式中：μ为联系度，表示集对之间的关联程度；N为集对特性总数；S为集对中相同的特性总数；P为集对中对立的特性总数；F为集对中既不相同也不对立的特性总数为联系数同一度、差异度和对立度，其中a+b+c=1，且a、b、c均为非负数；i为差异度标记系数，i∈［-1，1］；j为对立度系数，j∈［-1，1］，一般取j=-1。

3.2灰色关联度的集对分析模型

联系度函数 μ=a+bi+cj刻画了集对内部集合之间的关系，当两个集合趋于相同，i的取值为大；当两个集合趋于相反，i的取值为小。根据这一标准，由a、b和c约束值综合决定差异度系数i。针对差异度系数i的取值问题，可以利用灰色系统理论，对差异度与同一度、对立度分别进行灰色关联分析，对它们的相互密切程度进行量化，将较大的关联度赋予差异度系数i，合理地解决差异度系数的不确定问题［16］。

灰色系统是20世纪80年代由邓聚龙提出并创立的一个理论，主要研究灰色等不确定性问题。设评价数列为x0（j）（j=1，2，…，n），比较数列为xi（j），它们的关联系数为ξi（j），表达式见式（2）：

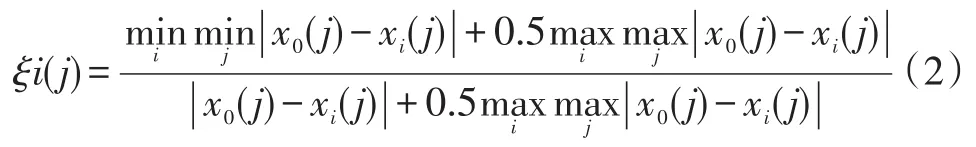
关联度表达式见式（3）：

关联度r越大，表示评价数列与比较数列越相近。

4　熵权法多属性决策模型

4.1多属性决策模型

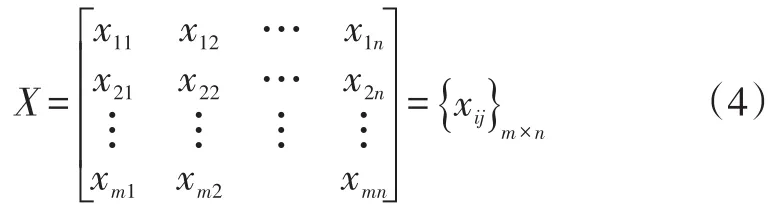
4.1.2建立最佳最差方案。一般来说，指标可以分为效益型指标和成本型指标，对于效益型指标，指标越大越好，效益型指标表示为γij=max（xij），对于成本型指标，指标越小越好，成本型指标表示为γij=min（xij），式中i=1，2，…，m，j=1，2，…，n。

根据效益型指标和成本型指标可以构造最佳和最差指标集合，分别设为Rgood、Rbad，见式（5）、式（6）［17］：

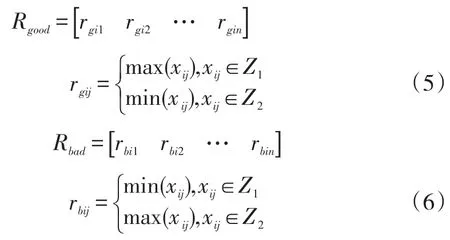
4.1.3构造最佳与最差同一度矩阵。计算被评价方案各指标xij与最佳方案和最差方案中γij的同一度，组成最佳和最差方案的同一度矩阵分别为A（见式（7））、B（见式（8））：

4.2熵权法确定权重系数

方案的综合评价需要确定各指标权重，最终综合评价集为（见式（9））：

式中：W-各指标权重，W=（ω1，ω2，…，ωm）。

V是综合了指标权重、最佳方案同一度、最差方案同一度而得出的，因此，可以根据V对方案进行排序。

指标权重确定的方法有Delphi法、层次分析法、熵值法等。Delphi法和层次分析法确定权重侧重于专家的经验，主要依靠专家对指标重要性的了解来对指标赋权，方法虽然相对简单，但缺点是会造成评价结果对专家存在不同程度的依赖，且可能由于人的主观因素而形成偏差。而熵值法主要根据评价对象的固有信息确定权重，它通过数理的运算来获得指标的信息权重，能尽量消除权重计算的人为干扰，使评价结果更客观。因此，为避免人为因素和主观因素影响造成的偏差，本文引入熵权法确定权重系数。熵权法的基本思想是认为指标的差异程度越大，熵值越小，其权重相应越大，该指标对综合评价的影响越大，即可以由评价指标值构成的判断矩阵通过计算熵值来确定指标权重。其计算步骤如下［1，5］：

构建m个方案n个评价指标的判断矩阵：

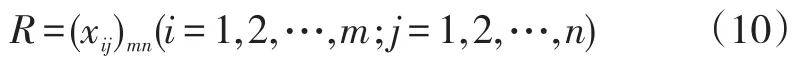
将判断矩阵R进行归一化，得到归一化矩阵B，B的元素为：

效益型指标：

成本型指标：

式中：maxxij和minxij分别为同一评价指标下不同方案中的最大值或最小值。

根据熵的定义，m个评价事物n个评价指标的熵为：

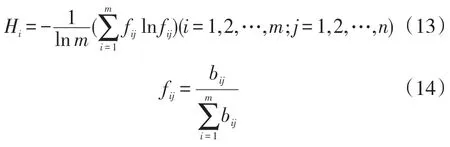
为使lnfij有意义，一般需要假定当fij=0时，fij1nfij= 0。但当fij=1，lnfij也等于零，这显然不切合实际，与熵所表述的含义相悖，故需对fij加以修正，将其定义为：

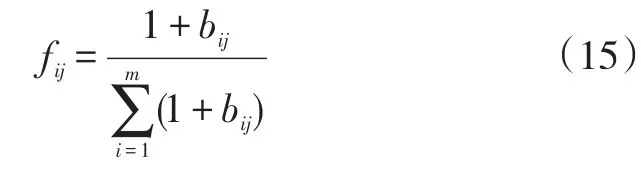
最后计算各评价指标的熵权，第j个评价指标的熵权为：

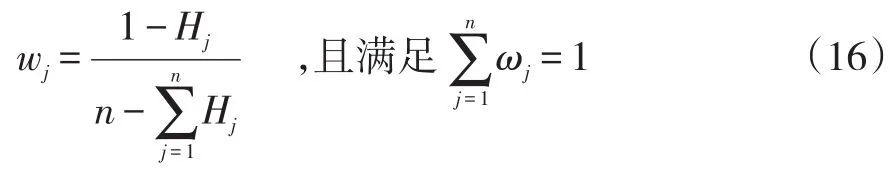
5　实例分析

5.1供应商基本信息

某绿色建筑项目承包商需要在5个原材料供应商（分别以字母A、B、C、D、E表示）之间选择一个合作伙伴，他们在建筑产品优势、企业运营管理、合作潜力和绿色管理方面具有各自的优势和劣势。为了选出最合适的供应商，对五家供应商的相关数据进行收集。考虑到有些指标难以量化评估，为了研究方便，仅选取其中有代表性的部分指标，最后确定的评价指标集为：产品优势用定量指标产品价格和产品合格率表示，运营管理用定量指标准时交货率和资产负债率反映，合作潜力和绿色管理难以用量化指标表示，直接表示为专家进行考察后给出的定性评价结果，归纳整理后的评价指标值见表1。其中，产品合格率、准时交货率、合作潜力和绿色管理属于效益型指标，产品价格和资产负债率属于成本型指标。

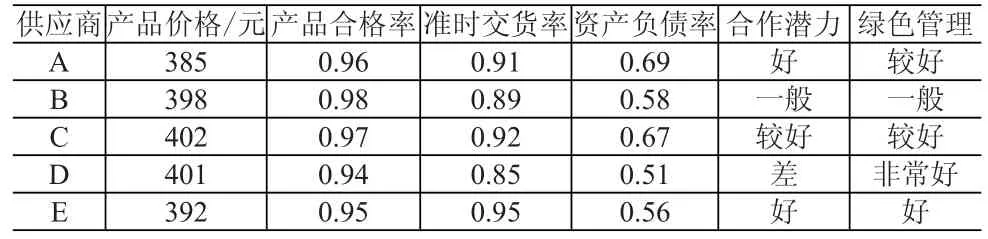
表1　各供应商的评价指标信息

5.2量化定性指标

在定性指标重要性比较中，需要对其进行定量化区间赋值，按照影响程度区分为五级，见表2。

表2　定性指标定量化

5.3确定等级

结合实际情况，给出等级标准，见表3。

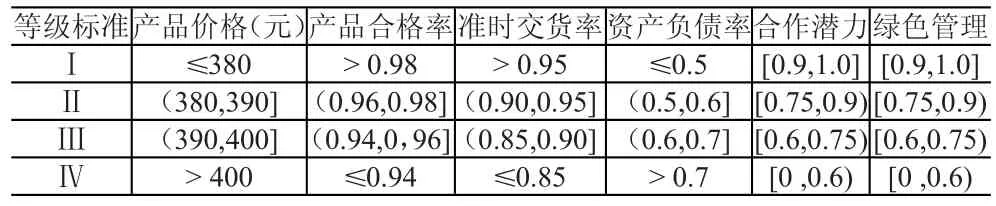
表3　供应商评价等级标准

将各供应商指标信息与评价等级标准建立集对，根据式（1），求出同一度、差异度、对立度，见表4。

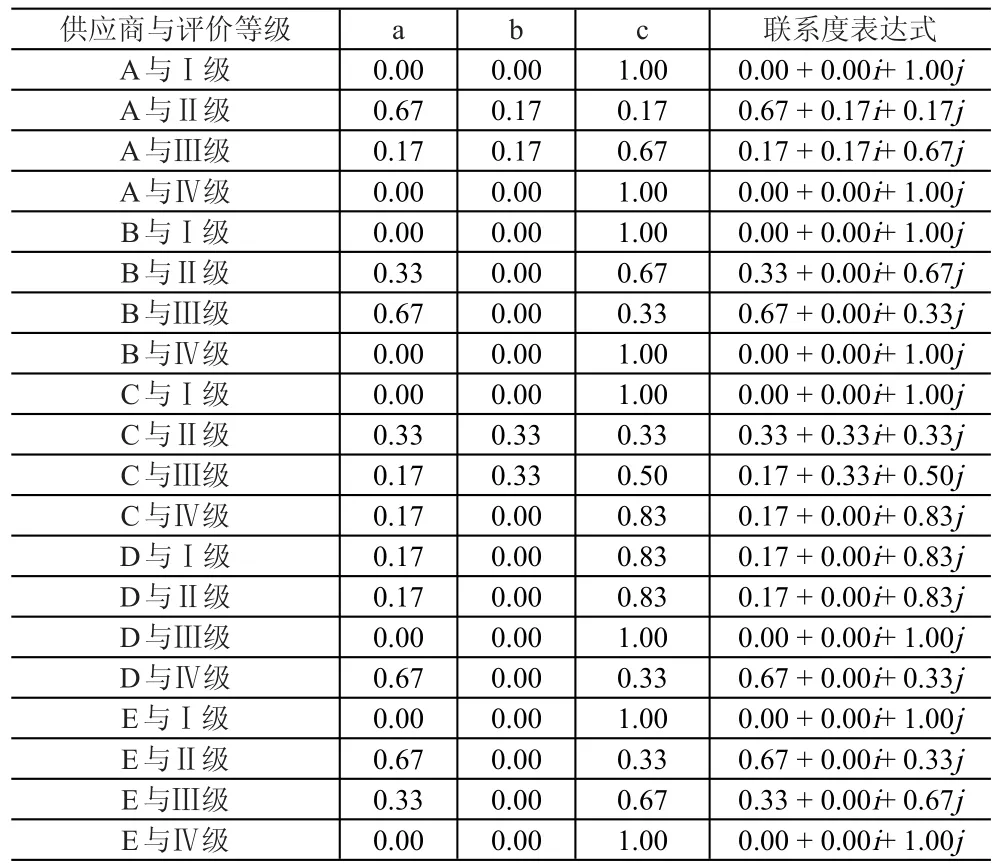
表4　各供应商与评价等级联系度信息表

为了确定差异度系数i的值，需要比较确定差异度b与同一度a及对立度c的联系度，利用式（2）和式（3）计算联系度，分别求得rab=0.754，rbc=0.485，即rab＞rac，可知差异度与同一度的关联度比其与对立度变化的关联度高，因此差异度系数i的量化值为0.754，将其代入表4最后列各式，得各供应商与各等级之间的联系度，见表5。

表5　各供应商与等级联系度系数

由表5可知，各供应商与等级标准联系度较高的为Ⅱ、Ⅲ、Ⅳ三级，其中，供应商A、C、E为Ⅱ级，供应商B为Ⅲ级，供应商D为Ⅳ级，且μ（A，Ⅱ）＞μ（E，Ⅱ）＞μ（C，Ⅱ），说明A为Ⅱ级比C为Ⅱ级的可信度高，而C为Ⅱ级又比E为Ⅱ级的可信度高。

5.4综合评价

5.4.1熵权法确定权重。定量指标因数的权重直接根据熵权法确定，利用式（9）-（16）进行计算。对于定性指标因数，利用中间中值法将区间数转化为确定数，再根据熵权法确定权重。经计算求得：H=（0.949，0.982，0.985，0.979，0.984，0.983），进而得到权重集为：W=（0.370，0.128，0.110，0.149，0.120，0.122）。可见，评价指标权重中，产品价格权重最大，且产品价格＞资产负债率＞产品合格率＞绿色管理＞合作潜力＞准时交货率。

5.4.2构造最佳方案及最差方案。根据式（5）和（6）构造最佳和最差方案，见表6。

表6　最佳和最差方案

5.4.3构造最佳和最差同一度矩阵。为便于计算，将定性评价指标区间值转化为中间值，利用式（7）和式（8），计算得最优最差方案矩阵如下：

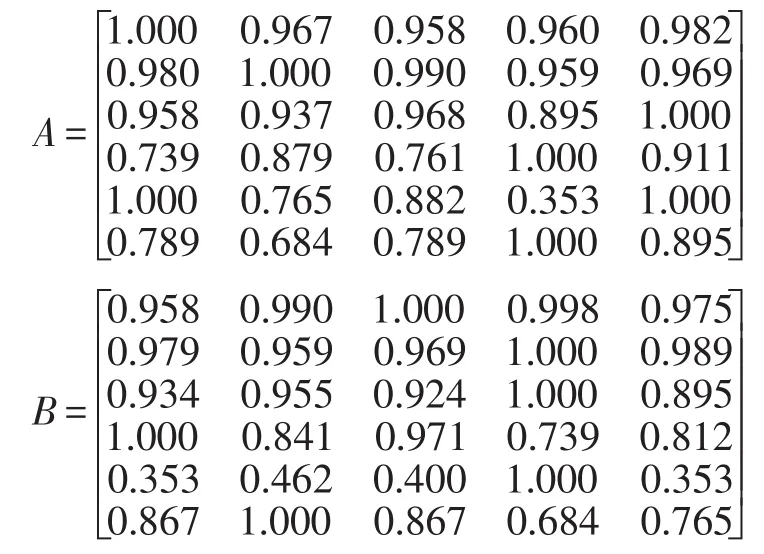
5.4.4供应商优劣排序。根据式（9），求得V=W（A-B）T=（0.048，-0.001，0.009，-0.032，0.120），即5个供应商的优劣顺序依次为A、E、C、B、D。其中，A为最优供应商，其次为E，最差供应商为D。

6　结语

对绿色建筑供应商的优选评价是一个复杂和充满不确定性的过程。本文在已有研究的基础上，围绕绿色建筑供应商的特点，从建筑产品优势、企业运营管理、合作潜力、绿色管理四个方面建立指标体系。考虑到评价指标的模糊不确定性，运用灰色系统理论和集对分析法，将各供应商指标信息与评价等级标准建立集对，充分考虑比较集的同一、对立、差异部分，得到各供应商与各等级之间的联系度，使评价结果更为合理、全面。在指标权重确定过程中，采用熵权法所确定的权重是以各供应商评价指标本身的差异性为基础，避免了以往确定权重过程带有的主观性，提高了决策的科学性和准确性。在综合评价过程中，利用最佳和最差方案相比较的方式，更加凸显各供应商优劣的差异性。由此，为绿色建筑供应商的选择评价提供了新的框架方法，也可为绿色建筑供应商的行动改进提供理论指导。

［1］王新艳，王新阳.基于熵权和VIKOR法的建筑供应商选择问题研究［J］.物流技术，2013，32（12）：154-156，229.

［2］宋冠秀.基于突变级数法的绿色建筑供应商选择［D］.天津：天津大学，2014.

［3］Kuo R J，Wang Y C，Tien F C.Integration of artificial neural network and MADA methods for green supplier selection［J］. Journal of Cleaner Production，2010，18（12）：1 161-1 170.

［4］Sanayei A，Farid Mousavi S，Yazdankhah A.Group decision making process for supplier selection with VIKOR under fuzzy environment［J］.Expert Systems with Applications，2010，37（1）：24-30.

［5］彭频，李静.基于熵权TOPSIS的建筑供应商选择问题研究［J］.江西理工大学学报，2010，31，（2）：67-69.

［6］吴立云，杨玉中.基于粗糙集-熵理论的绿色供应商选择模型研究［J］.工业工程与管理，2011，（2）：34-39.

［7］杨耀红，谭攀静.多目标智能加权灰靶决策在绿色供应链供应商选择中的应用［J］.华北水利水电学院学报，2012，33（2）：37-139.

［8］颜波，石平.基于超效率DEA模型的绿色供应链环境下供应商评价与选择［J］.决策参考，2013，（13）：37-40.［9］贾安超，周刚.基于粗糙集和BP神经网络的供应商选择研究［J］.物流技术，2012，（23）：229-232，267.

［10］齐宝库，刘霞，王欢.AHP-FUZZY综合评判方法在绿色供应链评价中的应用［J］.沈阳建筑大学学报（自然科学版），2012，（5）：955-960.

［11］徐茜，张琳，岳广飞.基于粗糙集的绿色建筑供应商价值诊断［J］.山东建筑大学学报，2013，28（4）：371-374.

［12］孔令祯，张云，杨骏，等.基于集对分析法的工程项目造价风险评价［J］.土木工程与管理学报，2016，33（1）：90-96.

［13］郑晓云，贾玲.住宅产业化进程中建筑部品供应商的选择研究［J］.华东经济管理，2013，27（10）：93-97.

［14］阮连法，陈佳玲.基于模糊VIKOR方法的绿色建筑供应商选择［J］.统计与决策，2011，（21）：62-65.

［15］Kan Yuan，Jiang Wei，Ji Xiao-juan.Intrusion detection model based on set pair analysis theory［J］.Future communication，computing，control and management，2012，（141）：35-42.

［16］李聪，陈建宏.联系数的物元模型在建筑安全评价及预测中的应用［J］.安全与环境学报，2016，16（2）：71-75.

［17］何美丽，刘浪，王宏伟，等.基于集对分析的工程评标未知权重多属性决策［J］.中南大学学报（自然科学版），2012，43（10）：4 057-4 062.

Selection of Green Construction Supplier Based on Grey Correlation and Set-pair Analysis

Yang Siling，Jiang Genmou
（School of Civil Engineering， South China Jiaotong University， Nanchang 330013， China）

In this paper， in view of the problems in the selection of the green construction suppliers and on the basis of currentresearches and surrounding the characteristics of the green construction supplier， we established the supplier comprehensive evaluation andselection system from the aspects of product advantage， corporate operation management， potential for cooperation， and green management.Then based on the set-pair analysis， we combined the deterministic and nondeterministic factors to establish the pair of the evaluation set andthe index set； then in connection with the grey correlation theory， we respectively analyzed quantitatively the correlation between thedifference and uniformity， and between the difference and contrast of the two； and at the end， we used the entropy method to weight theevaluation indexes and through building the positive and negative uniformity matrix， selected the optimal supplier. At the end， we used anempirical case to demonstrate the validity of the method in the evaluation and selection of the green construction suppliers.

green construction； supplier selection； grey correlation； set-pair analysis； entropy weight

TU-023；F274

A

1005-152X（2016）08-0106-05

10.3969/j.issn.1005-152X.2016.08.027

2016-07-11

教育部人文社会科学青年项目（14YJCZH186）；江西省科技厅软科学一般项目（20161BBA10045）；江西省自然科学基金（20151BAB216026）

杨斯玲（1985-），女，江西吉安人，博士，讲师，研究方向：建筑供应链与建筑管理；蒋根谋（1964-），男，江苏泰州人，博士，教授，研究方向：建筑经济与管理。