OWC波浪能采集气室内水动力学压强分析

杜小振，张　燕，朱文斗，文　傲，赵继强

（山东科技大学 机械电子工程学院，山东　青岛　266590）

OWC波浪能采集气室内水动力学压强分析

杜小振，张燕，朱文斗，文傲，赵继强

（山东科技大学 机械电子工程学院，山东青岛266590）

振荡水柱（Oscillation Water Column，OWC）是近年来发展较快的波浪能采集技术，该装置主要由箱体、振荡水柱和压缩空气柱组成，而波浪在气室内产生的压强对能量转换效率等起到决定作用。结合三维侧向开口的振荡水柱波能转换装置，基于线性波理论，采用三维Green函数法建立了气室内水气动力学性能的空气压强理论计算模型，利用多维切比雪夫（Chebyshev）多项式求解，计算结果精度高，能够准确表达波浪和结构设计参数对气室内压强影响。依据理论计算模型分析了波浪周期、波长、吃水深度、入射波幅等参数对气室内压强作用。

振荡水柱；入射波能；气室压强；波浪能发电

振荡水柱式（OWC）波能转换装置具有转换效率高、受地形影响小、装置可靠等优点。其发电基本原理：波浪进入气室在半封闭空间内产生压缩气柱并形成空气动能；利用空气透平转换成转轴旋转机械能，进而驱动发电机输出电能。国内外学者对OWC气室转换效率试验模式及其相关理论进行了相关的研究工作：刘月琴等［1］研究了岸式振荡水柱波能转换装置气室内的水面振荡与入射波周期的关系；梁光贤和刘臻等［2-3］测试分析了不同工况气室内波高受入射波周期、波幅、前墙吃水深度、气室宽度、底部斜角、出气口开口形式等因素的影响。焦建辉［4］测得OWC气室内压强随周期和波幅变化情况，Wilbert［5］等利用物理模型试验，测得气室内前墙、后墙、气室中间位置各测试点在同一时刻不同位置压强的变化波幅一致。K Toyota［6］采用流场边界条件求解速度势，并推导了流场速度势函数法求解流场某一点压强的计算公式并给出气室内压强计算方法。研究表明气室内波幅运动与压缩气柱产生的压强直接相关，波幅大则产生的压强大；同时，气室内压强受入射波周期、波幅、气室宽度、气柱高度、前墙吃水深度和底部斜角、出气口形状等因素影响。

为了研究气室内压强动力学特性，本文依据气室内同一时刻不同位置压强变化波幅基本一致，用三维Green函数法建立数学理论模型，如图1所示，其中1为出气孔，2前墙，3气室，4底板，5后墙。采用多维切比雪夫（Chebyshev）多项式计算气室内某一个坐标点的压强来分析，求解气室内压强，为振荡水柱波浪能发电的设计和分析提供理论依据。

图1　振荡水柱波能转换装置示意图

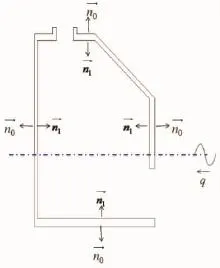
图2　内域和外域的表示

1　流场速度势求解

OWC波能转换装置为三维半潜体，简化为简易方箱结构，假定流体均匀、不可压缩、无粘性、无旋，忽略表面张力。气室内流场速度势求解分为气室内域区、外域区及内域和外域的衔接区，满足压力与速度连续条件［7］，用Green函数法求解。图2是由图1纵向刨切得到内外域的表示。

1.1内域理论计算

内域的划分，其正法向指向流体以外即装置外部，如图2所示。根据线性叠加原理，理想流体运动从t=0开始，有限时间t内，规则线性波流场内速度势为入射势和绕射势线性叠加，如式（1）：

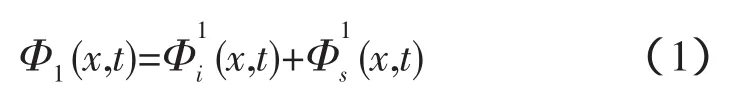
有限水深中单一频率、单一方向的入射波作用下，入射势Φ1i为：

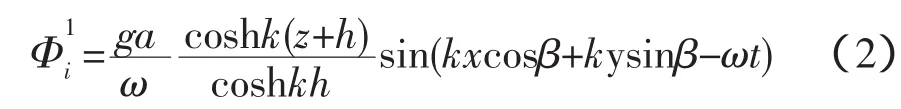
式中：h为水深；k为入射波的波数；β为入射波方向角。

由Green函数法根据定解条件求解波高H时入射波引起物体绕射速度势

1.2外域理论计算

外域的划分，其正法向指向流体以外箱体内部，如图2所示。外域SH2：X＞TL，d-h＜z＜d，相应速度势分别由式（5）～式（7）描述。

外域速度势为：

OWC外域绕射速度势，用Green函数法表示为：

1.3内外域的衔接理论计算

在内外域衔接面内、外侧即箱体开口处，流体速度与压力满足连续条件，保证内外域匹配，衔接条件为：

2　气室内空气压强计算

内域与箱体内空气衔接问题则假设箱体内空气压力按正弦变化，并与箱体内水面升沉速度成正比，以上讨论确定入射势Φi和绕射势Φs，则气室内压缩空气压强计算公式由式（1）得［9］：

式中：μ为气室内空气升降振荡有效阻尼系数。

3　时域内有限水深流场速度势Green函数的求解

3.1Green函数求解分析

用时域Green函数法直接求解水动力学问题时，需要对Green函数及其导数作卷积，同时由于波积函数的振荡和增幅特性，计算复杂、精度低。对三维有限水深Green函数，Clement和Mas［10-11］分别提出函数级数算法，计算过程中涉及到函数关于未知量的求导没有给出，导数的计算还需要根据给出的公式进一步推导；Newman［12］和Teng等［13］使用了Chebyshev多项式分区域逼近三维有限水深Green函数的算法，计算量较大；Wehausen和Laitone［14］以三维脉动源的形式给出了满足边界条件的Green函数如下：

式中：δ为脉冲源；g为重力加速度；h为水深；B0为零阶贝塞尔函数；R是场点和源点的水平距离；r是场点和源点的距离；r1是场点和源点关于水底面镜像的距离。由于式中含有正弦函数和Bessel函数，在积分过程中收敛缓慢，不能直接进行计算。Newnan［12］对参数g和h采用下式定义无量纲变量：

据此，Green函数可以表示为：

3.2Green函数采用Chebyshev多项式逼近法计算分析

为了迅速求解G0（X，V），需要避免无穷积分，则作如下处理：

（1）当X＞1时，对G0使用Fourier级数法表示：

式中：K0为修正汉克尔函数。

（2）当0≤X≤1，采用Chebyshev多项式逼近G0（X，V），表示为：

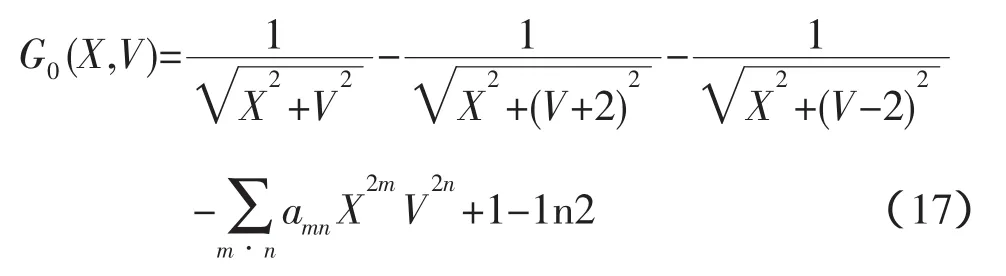
式中：amn为分析Green函数在各种参数范围内的特性确定的快速计算插值系数。

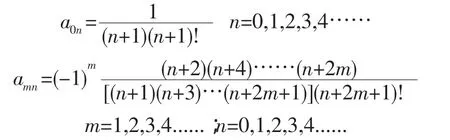
在近场（0≤X≤1）情况下，对多项式G0（X，V）求偏导，表示为：

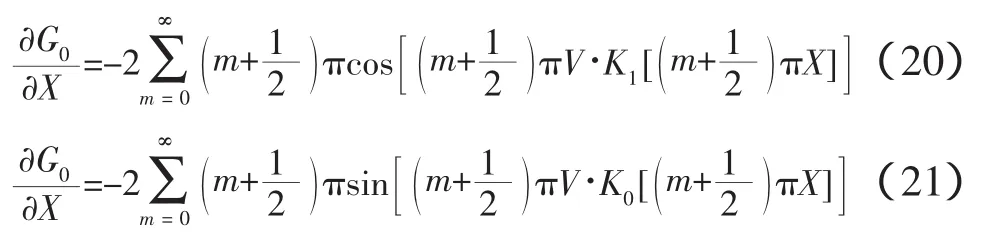
在远场（X＞1）情况下，G0求偏导表示为：

求解G1（X，V，T）时，当场点和源点接近时将涉及奇点问题，具有高速振荡和不易收敛的特点，因此计算时需要分离出高速振荡项G1∞，采用求和形式计算G1（X，V，T），表示为：

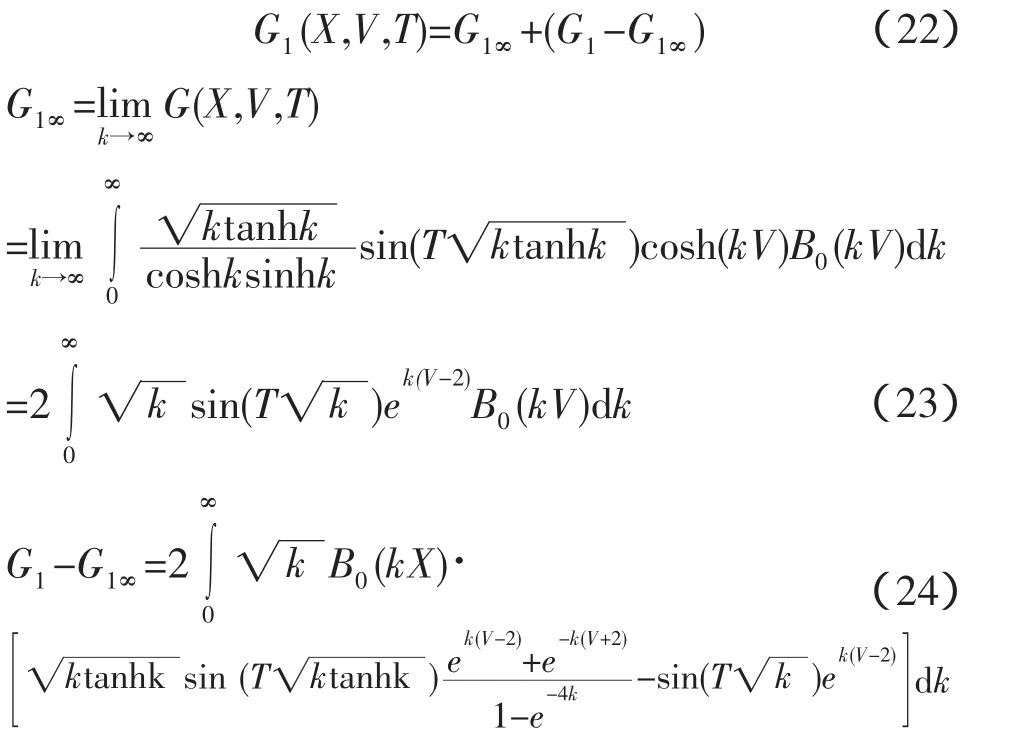
G1∞（X，V，T）转化为球坐标系（r，θ）下，角度θ从垂轴的负轴方向量起，关于r无量纲化，各个变量代替如下将3个自变量减少为两个自由变量，G1∞可变换为：

G1∞对X求偏导计算，得：

G1-G1∞对X求偏导计算，得：

4　气室压强影响因素分析

振荡水柱波能转换气室理论分析设计结构长为1.2 m、宽为1.0 m、高为1.5 m。波长是气室内压强的影响因素之一，受入射波周期的影响，如图3所示。当入射波周期逐渐增大时，会导致气室内的波高变大，从而形成较高气室压强。

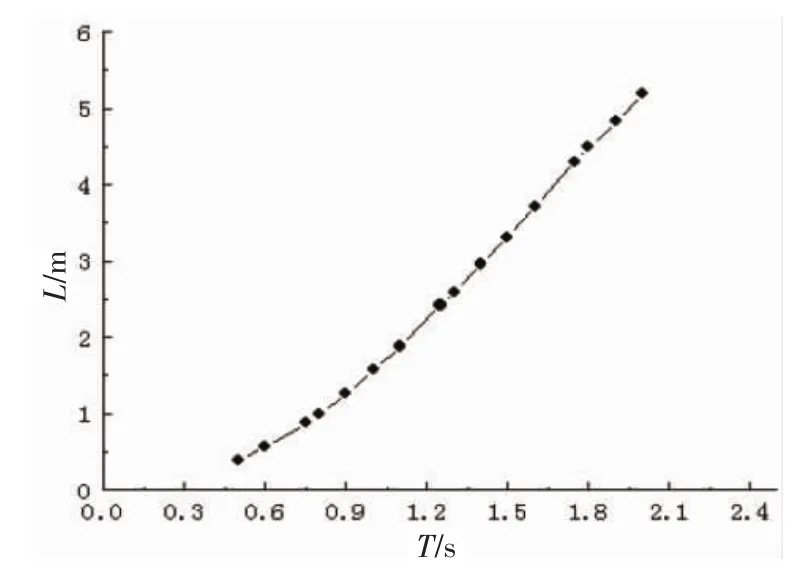
图3　波长随周期的变化

图4　压强随周期的变化

OWC气室内的压强随周期的变化曲线如图4所示，本文基于水动力理论采用三维Green函数法建立物理模型计算的数值曲线A与文献［4］的试验数值曲线B的变化幅度基本一致，同时与耿楠［15］建立的物理模型测试得压强幅值相吻合。T＜2 s采用三维Green函数法计算压强随入射波周期T增大而提高，T＞2 s压强随周期T的增大而减小。经分析，当T=2 s的时候，到达气室前墙的入射波与气室内的波面产生共振，OWC气室内压强峰值为46 Pa。当入射波周期逐渐增大时，会导致气室内的波高也逐渐变大，压强升高，当入射波高增加到一定值后，气室内波幅增大带来的非线性产生波能的内部损耗变强，导致气室内波高逐渐减小，压强随之降低。

波浪周期T=1 s，波高0.4 m，水深h=1 m，计算得波长L=1.57 m。气室内压强随吃水深度d变化如图5，d＜0.3 m，前墙吃水深度增加引起气室内波高逐渐增大，进而引起气室内压强增加；d=0.3 m时，压强峰值63 Pa；d＞0.3 m，吃水深度d增加，气室内反射波能增多，其与入射波能相互抵消，从而引起压强逐渐减小。采用三维Green函数法计算气室内压强随入射波幅变化如图6所示，入射波幅对OWC气室内压强影响明显，波幅增大压强升高。

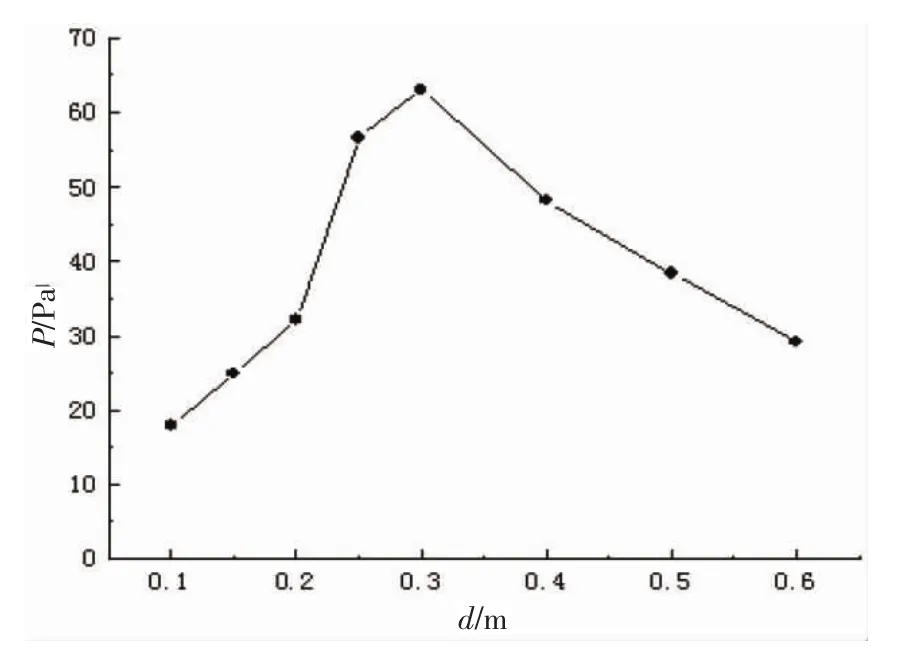
图5　压强随吃水深度的变化

图6　压强随波幅的变化

5　结论

采用三维Green函数法建立了气室内水气动力学的压缩气柱压强理论模型，分析气室内压强性能的影响因素。计算过程采用多维Chebyshev多项式和渐近展开式快速近似计算方法可精确快速求解三维Green函数，根据离散化方法求解出三维脉动源源强、绕射势等，求解流场内总速度势关于时间导数得到气室内压缩空气压强值。计算结果表明：采用三维Green函数法建立的水气动力学模型所得气室压强数值与测试结果吻合，求解结果精确度高，能准确分析OWC气室内压强水动力学特性。数值分析结果显示气室内的压强受波长、波浪周期、波幅和吃水深度等因素的影响显著，以上分析为OWC设计和研究提供理论参考。

附注

为格林函数的记忆项表达式的无量纲形式，由于函数G1具有高速振荡，不易收敛的特点，计算时分离出高速振荡项G1∞，采用求和的形式计算G1= G1∞+（G1-G1∞）。其中G1∞为类似于无限水深时域格林函数的表达式，计算比较复杂，需进一步分析。（G1-G1∞）为有限水深和无限水深时域格林函数之差，变化较为平缓，易于计算。

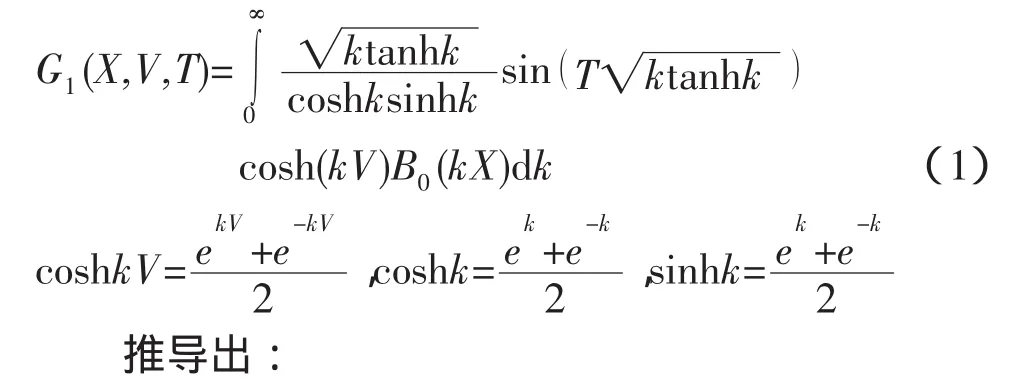
式（3）～式（6）转化为球坐标系（r，θ）下，角度θ从垂轴的负轴方向量起，关于r无量纲化，各个变量代替如下:

将三个自变量减少为两个自由变量，式（3）可变换为：

［1］刘月琴，武强.岸式波力发电装置水动力性能试验研究［J］.海洋工程，2002，20（4）：93-97.

［2］梁贤光，孙培亚，游亚戈.汕尾100kW波力电站气室模型性能试验［J］.海洋工程，2003，21（1）：113-116.

［3］刘臻.岸式振荡水柱波能发电装置试验及数值模拟研究［D］.青岛：中国海洋大学，2008.

［4］焦建辉.OWC发电装置二次能量转换系统的优化设计研究［D］.青岛：中国海洋大学，2011.

［5］Wilbert R.Wave Interaction With a Double Chamber Oscillating Water Column Device［J］.Ocean and Climate Systems，2013，11（4）：21-39.

［6］K Toyota.Research for Evaluating Performance of OWC-Type Wave Energy Converter“Backward Bent Duct Buoy”［C］//Institute of Ocean EnergySaga University，HonjyoBanchi Saga-City，Japan，2009（8）：901-913.

［7］韩凌.应用时域格林函数方法模拟有限水深中波浪对结构物的作用［D］.大连：大连理工大学，2005.

［8］Beck R F，Liapis S.Transient Motions ofFloatingBodies at ZeroForward Speed［J］.Journal ofShip Research，1987，31（3）：164-176.

［9］陶尧森，沈志东.三维振荡水柱波能转换装置的流体动力计算［J］.水动力学研究与进展，1988，3（4）：85-96.

［10］Clement A，Mas S.Computation ofthe Finite Depth Time-Domain Green Function in the Small Time Range［C］//9th Intl Workshop on Water Waves and FloatingBodies，Kyushu，Japan，1994.

［11］Mas S，Clement A.Computation ofthe Finite Depth Time-Domain Green Function in the Large Time Range［C］//10th Intl Workshop on Water Waves and FloatingBodies，Oxford，UK，1995.

［12］Newman J N.The Approximation of Free-Surface Green Functions［C］//Wave Asymptotic，Proceeding of Fritz Ursell Retirement Meeting，Cambridge UniversityPress，London，1990.

［13］TengBin，Han Ling，Gou Ying.FastEvaluation ofTime-Domain Green Function for Finite Water Depth［J］.China Ocean Engineering，2003，17（3）：417-426.

［14］Wehausen J V，Laitone E V.Surface Waves［M］.Berlin：Handbuch der Physik.9，Springer Verlag，1960.

［15］耿楠.振荡水柱波能转换器效率分析及改进方案研究［D］.长沙：湖南大学，2012.

Analysis on the Hydrodynamic Pressure in the OWC Air Chamber for Wave Energy Harvesting

DU Xiao-zhen，ZHANG Yan，ZHU Wen-dou，WEN Ao，ZHAO Ji-qiang
College of Mechanical and Electronic Engineering，Shandong University of Science and Technology，Qingdao 266590，Shandong Province，China

The oscillating water column（OWC）technology is developing rapidly in recent years for wave energy harvesting.This device includes box body，oscillating water column and compressed air column.The pressure induced by the wave in the air chamber will significantly influence the conversion efficiency from wave energy.The theoretical calculation model of air pressure is derived with the three-dimensional Green function method and solved with Chebyshev polynomial.The results accurately reflect the pressure in the air chamber with a variety of factors，for example，the wave period，wave length，the depth of the draft and the incident wave amplitude.

Oscillation Water Column（OWC）；incident wave energy；gas chamber pressure；wave energy generation

P743.2

A

1003-2029（2016）04-0081-06

10.3969/j.issn.1003-2029.2016.04.015

2016-01-08

国家自然科学基金资助项目（51105234）；中国博士后科学基金资助项目；山东省科技发展计划资助项目（2013YD04018）；青岛市黄岛区科技项目小微企业发展和孵化器专项（2014-1-107）和应用研究与公共卫生专项（2014-1-42）资助；山东省高等学校优秀中青年骨干教师国际合作培养项目资助；青岛市博士后基金资助项目。

杜小振，男（1978-），博士，副教授，主要研究方向为微电源，海洋能发电和传感器技术等。E-mail：du_xzh@163.com