单层网壳结构非线性稳定的随机缺陷模态法研究*
魏德敏 涂家明
(华南理工大学 土木与交通学院,广东 广州 510640)
单层网壳结构非线性稳定的随机缺陷模态法研究*
魏德敏涂家明
(华南理工大学 土木与交通学院,广东 广州 510640)
采用随机缺陷模态法对凯威特-联方型单层网壳进行非线性稳定分析,研究了随机缺陷空间样本数量、矢跨比等因素对网壳结构稳定极限荷载的影响,并将随机缺陷模态法计算结果与一致缺陷模态法计算结果进行了对比.结果表明:采用概率统计方法对该网壳进行稳定分析时,随机缺陷样本数量应不小于90;对于矢跨比较大的单层网壳结构,采用一致缺陷模态法计算稳定临界荷载的概率可靠度较低,需要采用随机缺陷模态法加以验证;当网壳结构的矢跨比小于1/6时,两种初始缺陷分布方法计算出的稳定承载力较为接近.
单层网壳;随机缺陷模态法;一致缺陷模态法;非线性分析;矢跨比;稳定极限荷载
大跨度单层网壳属于缺陷敏感型结构.由于施工技术和施工质量等原因,单层网壳结构的初始几何缺陷不可避免,并且直接影响到结构的稳定性.
目前常用的结构初始几何缺陷确定方法有一致缺陷模态法和随机缺陷模态法.Papadopouios等[1]基于蒙特-卡洛法提出一种快速算法——随机有限元法,并对有随机缺陷的网壳结构的屈曲荷载进行研究.Gordini等[2-3]采用随机缺陷法研究了杆件初始弯曲及长度缺陷对双层网壳结构承载能力的影响.Bruno等[4]提出采用节点等效几何缺陷法研究初始缺陷对单层网壳稳定性的影响.Qi等[5]基于初始弯曲和残余应力的影响提出了计算网壳设计承载力的方法.赵海等[6]基于随机场展开法提出了高效寻求网壳结构初始缺陷的最不利分布形式的方法.刘慧娟等[7]提出随机缺陷模态迭加法来获得单层网壳结构最不利缺陷分布下的稳定承载力.卢家森等[8]提出了使用凸集模型确定单层球面网壳最不利初始几何缺陷的有效方法.此外,刘学春等[9]采用施工偏差概率法模拟弦支穹顶结构的初始几何缺陷;陈世英等[10]发现优化寻优结果与初始几何缺陷分布有直接关系;蔡健等[11]提出了计算量较少的N阶特征缺陷模态法计算网壳结构的稳定承载力.
本研究分别采用随机缺陷模态法和一致缺陷模态法对大跨度单层网壳结构进行非线性稳定分析,研究了随机缺陷样本数量、矢跨比等因素对网壳结构稳定极限荷载的影响,给出所需最少空间样本数目,并对两种方法的计算结果进行了对比分析.
1 随机缺陷模态法
随机缺陷模态法假定:结构每个节点的安装偏差均符合二倍均方差范围内的正态概率密度函数[12],即每个节点安装偏差随机变量为RX/2,其中X服从标准正态分布,R为节点最大安装偏差;各节点位置偏差随机变量是相互独立的.
由此可知,每一个样本空间点对应一种可能的初始几何缺陷分布模式(样本),可以计算出一个相应的稳定极限荷载值(样本值).因此由n个初始几何缺陷样本可以得到n个稳定极限荷载样本值.
随机缺陷模态法主要计算步骤如下:
步骤1确定最大安装偏差R,调用高斯随机分布函数生成坐标偏差,引入坐标偏差修改完善结构的节点坐标,形成初始几何缺陷分布形式,通过非线性屈曲分析,得到稳定极限荷载值,形成样本空间的一个样本值;
步骤2根据预先确定的样本空间数目n,重复步骤1进行非线性屈曲分析,得到n个极限荷载值,即样本空间的n个样本值;
步骤3运用概率与数理统计知识对样本值进行分布检验,确定结构最终的稳定极限荷载值.
2 工程算例
文中以跨度L=70 m,高度H=10 m,矢跨比H/L=1/7的凯威特_联方型单层球面网壳为算例.网壳总频数为9,而联方与凯威特的频数比为6∶3,凯威特肋环与斜杆分别采用φ278 mm×7 mm和φ226 mm×6 mm的圆钢管,联方斜杆和环杆分别采用φ252 mm×7 mm和φ206 mm×6 mm的圆钢管.钢材的弹性模量为E=206 GPa,泊松比ν=0.3,密度ρ=7 850 kg/m3.材料为理想弹塑性,满足Von Mises屈服准则,其屈服强度σ0=235 N/mm2.网壳结构的永久荷载和活荷载均为0.5 kN/m2,活载满跨布置,方向竖直向下.网壳与下部结构的连接为铰接.
网壳结构的有限元分析模型如图1所示.每根杆件划分为3个BEAM188单元[13].非线性方程求解方法为弧长法,收敛准则为力的收敛准则,以下所有非线性分析都做同样处理.
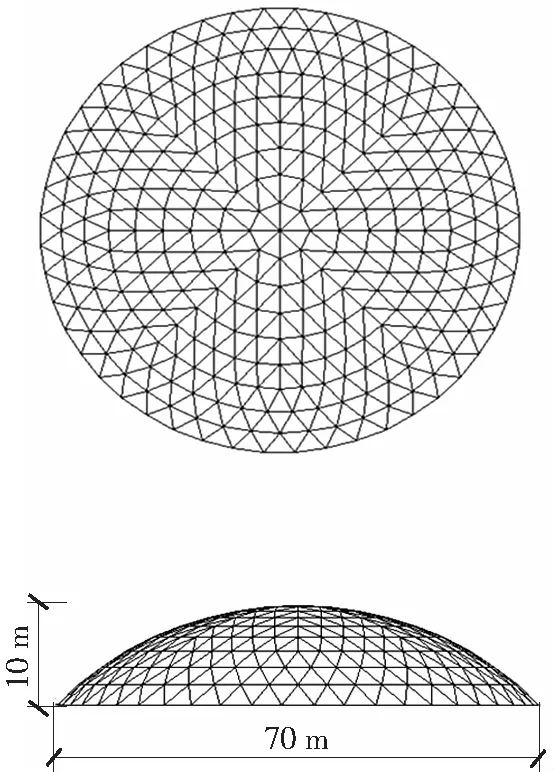
图1 网壳结构计算模型
选取初始几何缺陷的空间样本数n=200,按照文献[14]的要求,网壳结构最大初始缺陷值为R=L/300,由非线性有限元分析得到的结构稳定极限荷载Pcr如图2所示.
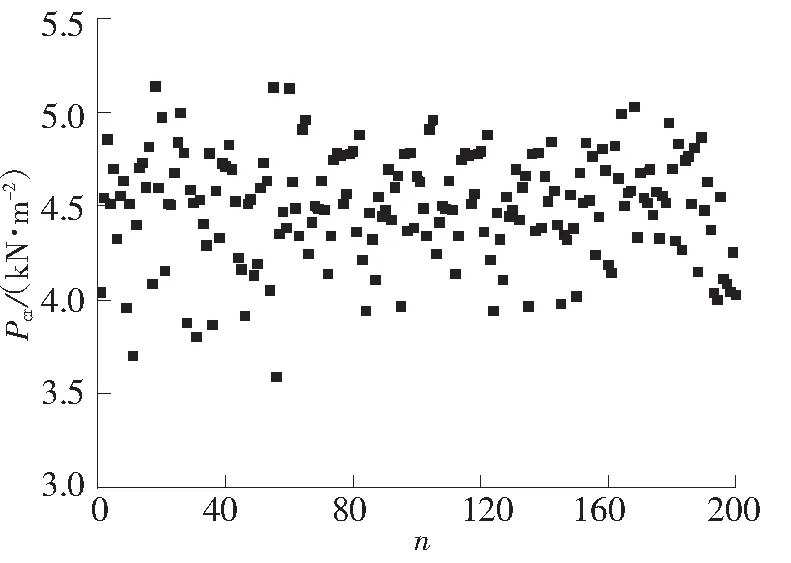
图2 网壳结构的稳定极限荷载
由图2和相应计算结果可知,该网壳结构的稳定极限荷载Pcr的最大值为5.133 kN/m2,最小值为3.585 kN/m2.如无特别说明,后文中Pcr单位为kN/m2.
图3给出200个样本值的分布直方图.由图3可以看出,这些样本值呈中间高两边低,接近于正态分布.以下利用概率密度函数f(x)对样本值进行χ2优度检验:
(1)
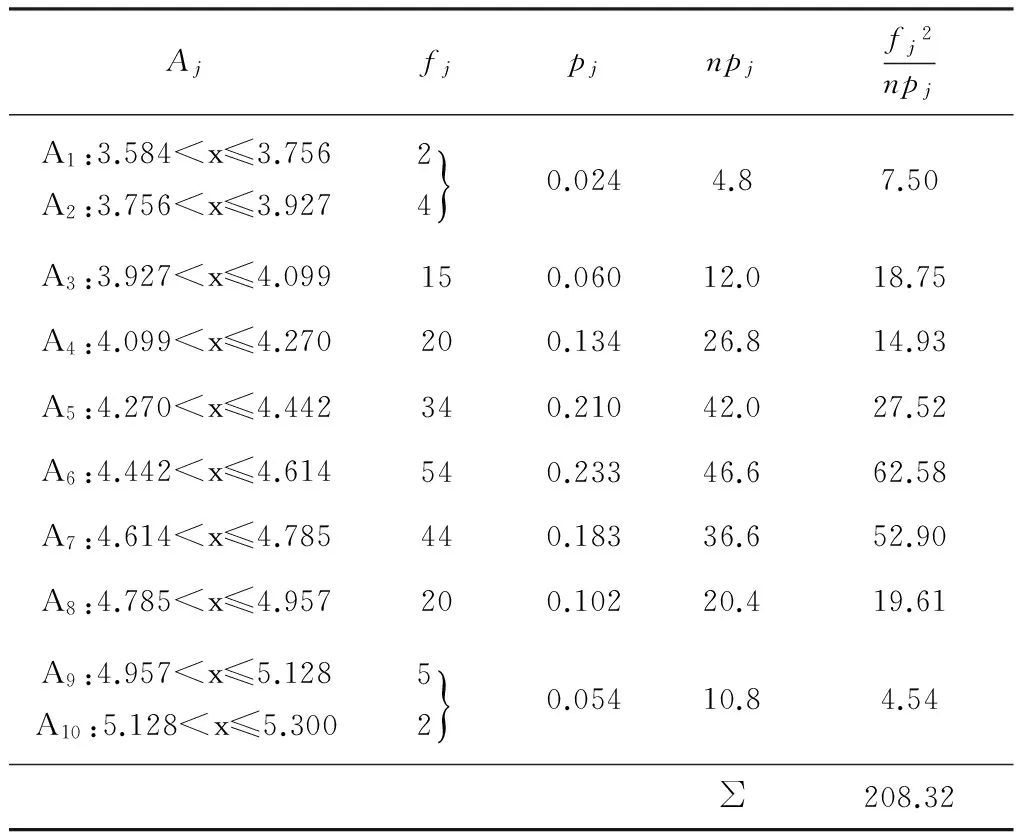
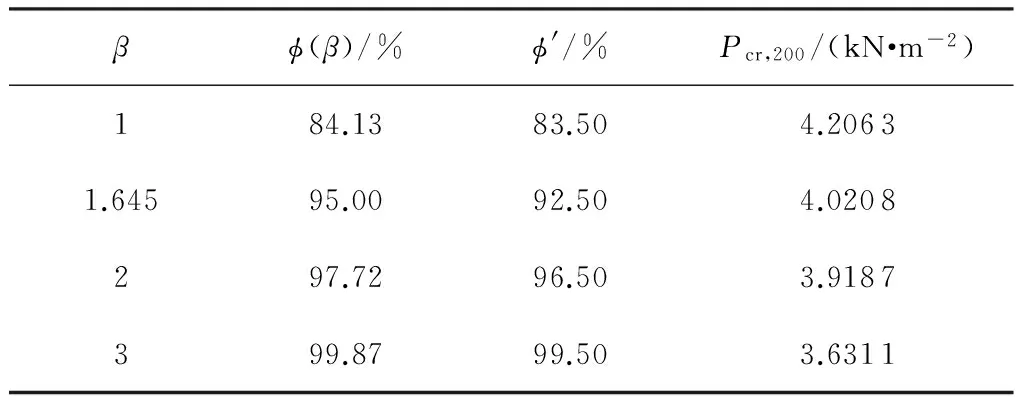
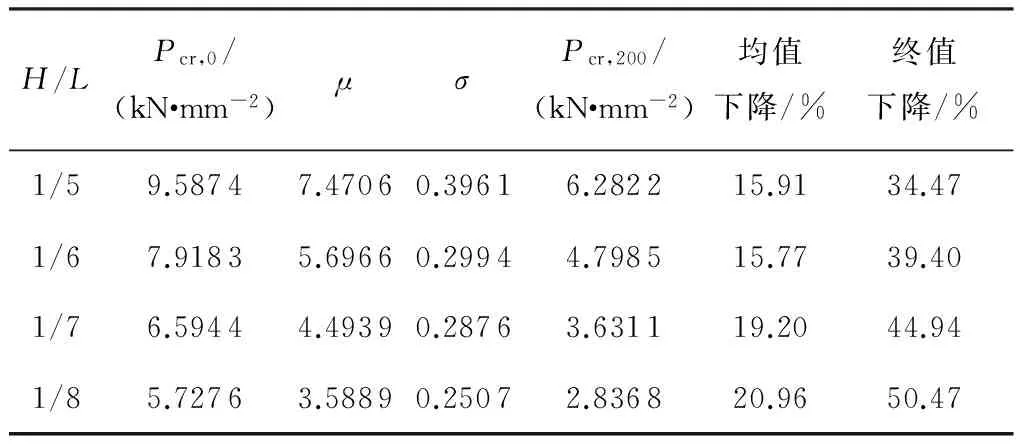
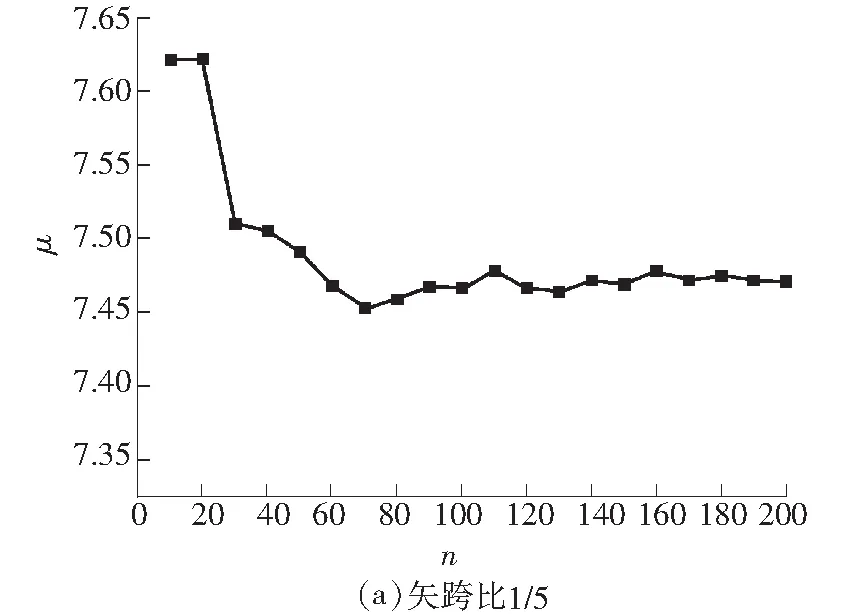
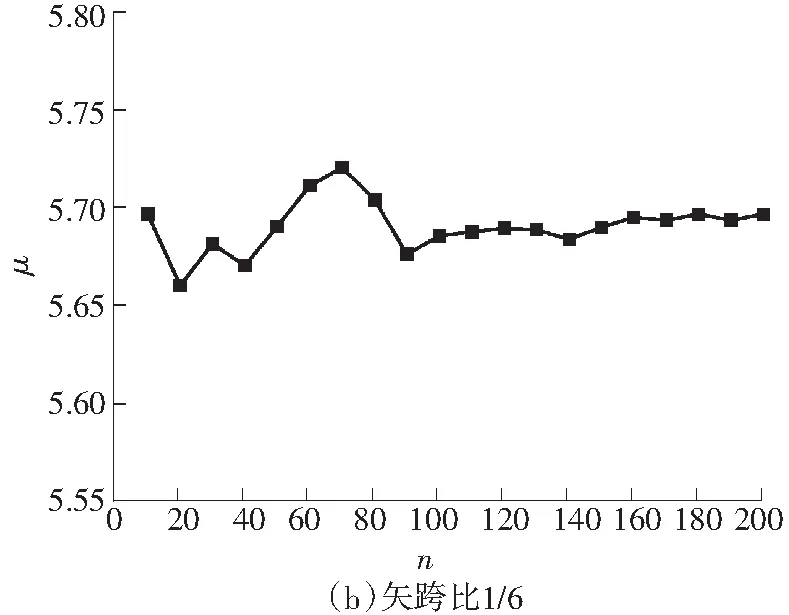
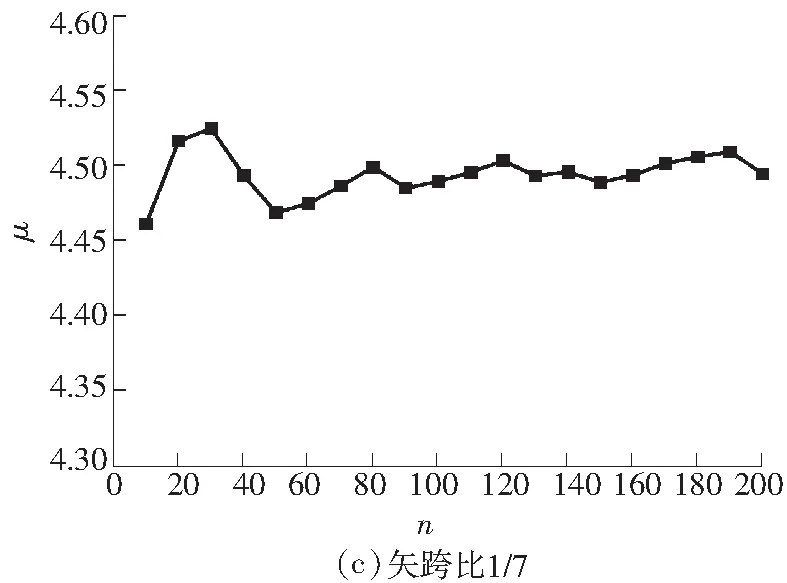
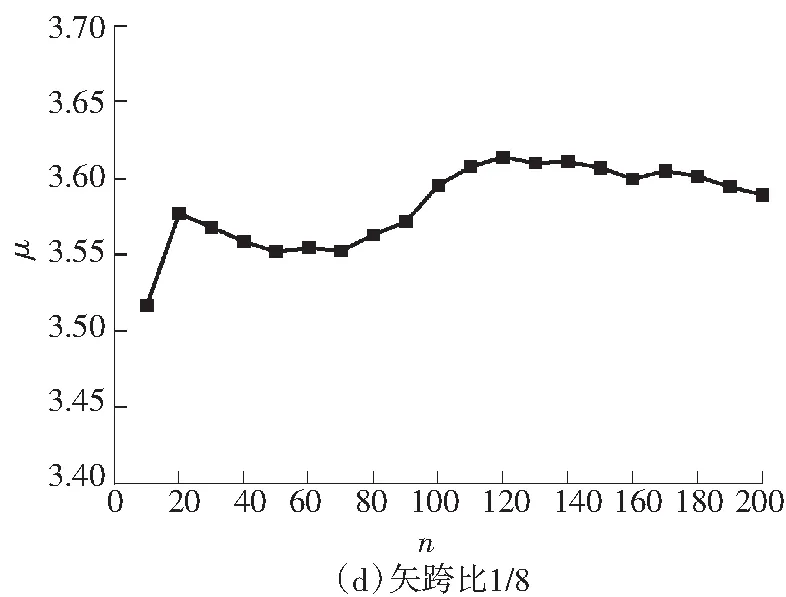
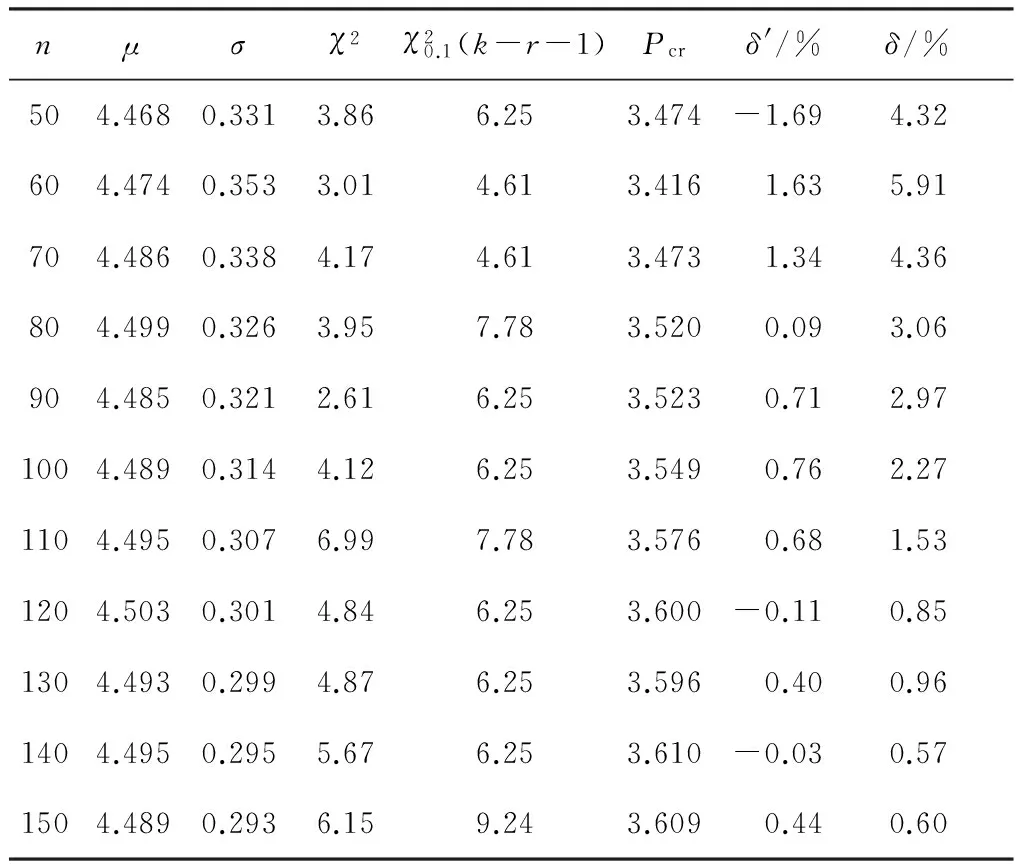
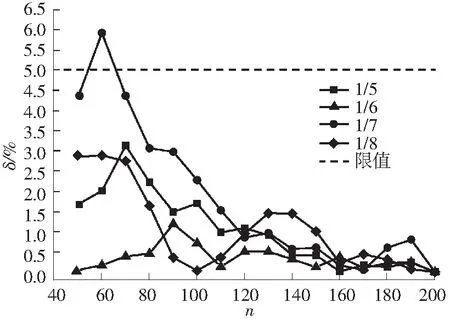
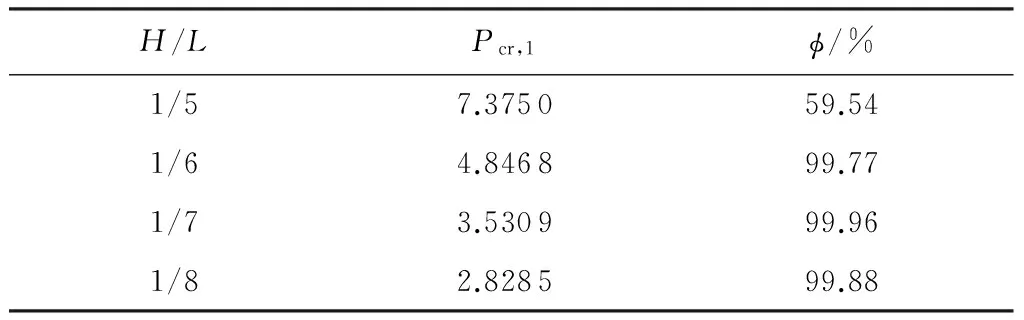
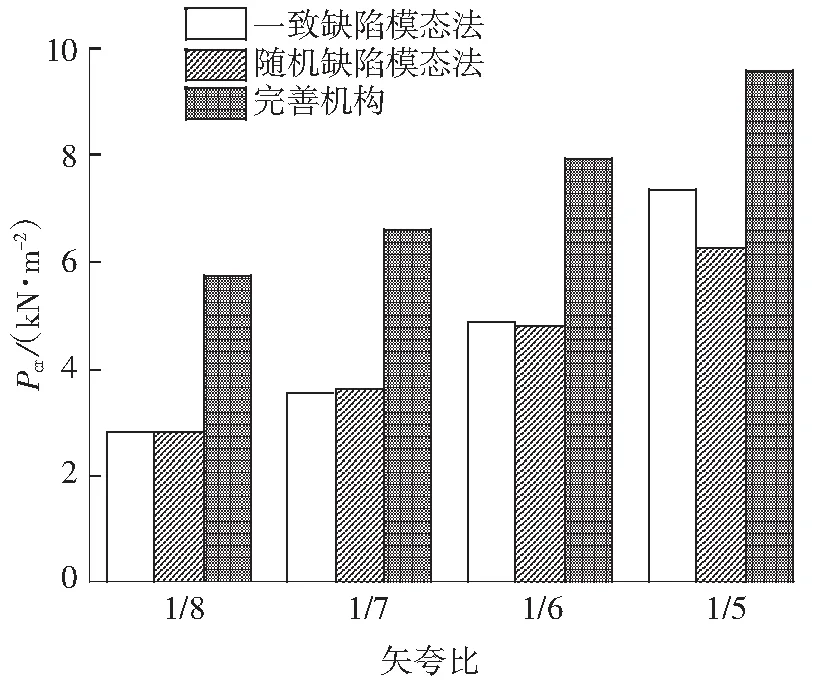
式中,3.584 图3 稳定极限荷载分布直方图 由极大似然估计法可得: (2) (3) 取n=200,由式(2)和(3)可得上述200个样本均值和方差μ=4.493 9,σ2=0.082 7,将μ、σ2代入式(1)可得X的概率密度函数的表达式为 (4) (3.584 将样本值X的可能取值区间(3.584,5.300)分为10个小区间,取事件Aj为第j个区间(j=1,2,…,10),得到表1所示χ2检验计算结果.表中χ2优度检验时小于5的分组就近合并,fj为落入区间Aj的样本值个数,pj为公式(4)在区间Aj上的积分概率. 表1 优度检验计算结果 由表1可得: χ2=208.32-200=8.32. 在显著水平0.1情况下[15],由表1知分组数k=8,未知量r=2,则: (5) 随机变量不同情况下,最终稳定极限荷载值及其保证率如表2所示.表中取实际保证率φ′=Ni/200,Ni为样本值不小于Pcr,200的样本数目. 表2最终稳定极限荷载值及其保证率 Table2Finalvalueofstableultimateloadsanditsguaranteerate βϕ(β)/%ϕ'/%Pcr,200/(kN·m-2)184.1383.504.20631.64595.0092.504.0208297.7296.503.9187399.8799.503.6311 一般情况下实际统计的保证率小于理论计算的保证率.从表2可知,随机变量β取值越大,所得最终稳定极限荷载的保证率理论值也越大,且保证率的理论值与实际值越接近.因此,在工程实际中一般取β≥2.文中取β=3时,所计算的200个样本值xi中只有1个低于最终稳定极限荷载,失效概率为0.5%. 3.1矢跨比对稳定极限荷载计算结果的影响 不改变杆件截面尺寸和组成形式,不同矢跨比情况下的单层网壳结构非线性稳定性的随机缺陷模态法分析结果如表3所示,样本数n取200,最大初始缺陷分别为L/300.表中Pcr,0和Pcr,200分别为完善和有随机几何缺陷单层网壳结构的稳定极限荷载.均值下降和终值下降分别指μ和Pcr,200相对于Pcr,0的下降值. 表3不同矢跨比下单层网壳结构非线性稳定性分析结果 Table 3Results of nonlinear stability analysis of the single layer reticulated shell under different rise span ratios H/LPcr,0/(kN·mm-2)μσPcr,200/(kN·mm-2)均值下降/%终值下降/%1/59.58747.47060.39616.282215.9134.471/67.91835.69660.29944.798515.7739.401/76.59444.49390.28763.631119.2044.941/85.72763.58890.25072.836820.9650.47 从表3可知,考虑初始几何缺陷后,单层网壳结构的稳定极限荷载相对于完善结构有较大幅度的下降,最大下降率达到50.47%;随着矢跨比的减小,网壳结构稳定极限荷载终值下降的幅度有所增大.因此初始几何缺陷对小矢跨比单层网壳结构稳定性的影响较大. 3.2样本数量对稳定极限荷载计算结果的影响 图4 μn关系曲线 图4可知,对于不同矢跨比的单层网壳,都呈现样本均值μ随着n的增大逐渐趋于稳定的规律;在n≥70时,矢跨比为1/5和1/7的单层网壳的μ值趋于稳定;在n≥100时,矢跨比为1/8的单层网壳的μ值才趋于稳定.说明小矢跨比的单层网壳对于随机几何初始缺陷更为敏感,数值也更难趋于稳定. (6) 相邻组的变化率用δ′表示. 考虑篇幅限制,表4给出了矢跨比为1/7的单层网壳样本数n=50,60,70,80,90,100,110,120,130,140,150的计算结果,其中k和r为每个样本进行优度检验的分组数和未知量.从表4的计算结果可以看出,当样本数n≥80时,相邻组稳定极限荷载的变化率均小于1%.Pcr,n与Pcr,200的相对误差δ随着样本数的增大先增大后减小,当样本数n>60时,相对误差δ均小于5%. 表4矢跨比为1/7的网壳的部分计算结果 Table 4Some computational results of the shell with rise-span ratio being 1/7 nμσχ2χ20.1(k-r-1)Pcrδ'/%δ/%504.4680.3313.866.253.474-1.694.32604.4740.3533.014.613.4161.635.91704.4860.3384.174.613.4731.344.36804.4990.3263.957.783.5200.093.06904.4850.3212.616.253.5230.712.971004.4890.3144.126.253.5490.762.271104.4950.3076.997.783.5760.681.531204.5030.3014.846.253.600-0.110.851304.4930.2994.876.253.5960.400.961404.4950.2955.676.253.610-0.030.571504.4890.2936.159.243.6090.440.60 不同矢跨比的单层网壳结构δ和δ′随n的变化情况如图5和图6所示. 图5 不同矢跨比网壳的δ变化曲线 Fig.5δvariation curves of the shells with different rise-span ratios 图6 不同矢跨比网壳的δ′变化曲线 Fig.6δ′ variation curves of the shells with different rise-span ratios 一致缺陷模态法认为网壳结构的最低阶屈曲模态对应势能最小状态,当结构的缺陷分布形式与最低阶屈曲模态吻合时,最容易发生屈曲.因此我国相关规程建议采用一致缺陷模态法进行网壳稳定性分析[14]. 4.1一致缺陷法计算结果 一致缺陷模态法得到的稳定极限荷载Pcr,1以及基于随机缺陷模态法计算结果的概率保证率φ如表5所示. 由表5可知,当矢跨比H/L<1/5时,一致缺陷法得到的稳定极限荷载概率保证率较高,且随着矢跨比的减小而增大.矢跨比H/L=1/5单层网壳结构的稳定极限荷载的概率保证率仅为59.54%.因此采用最低阶屈曲模态作为初始几何缺陷分布形式计算大矢跨比网壳的稳定极限荷载要慎重[17]. 表5一致缺陷模态法分析结果及保证率 Table 5Analysis results by use of consistent mode imperfection method and their guarantee rate H/LPcr,1ϕ/%1/57.375059.541/64.846899.771/73.530999.961/82.828599.88 4.2两种方法计算结果对比 一致缺陷模态法和随机缺陷模态法稳定极限荷载的计算结果如图7所示. 图7 两种方法计算结果的对比 由图7可知,稳定极限荷载随着矢跨比的减小而降低,完善结构的稳定极限荷载大于有初始缺陷的结构.矢跨比≥1/6,两种缺陷分布模态法计算得到的稳定极限荷载差别随着矢跨比的增大而增大.当单层网壳的矢跨比≤1/6时,两种缺陷分布方法的计算结果基本吻合,因此,初始几何缺陷分布形式对小矢跨比单层网壳结构的稳定极限荷载影响较小,可用一致缺陷法计算. 对于矢跨比大于1/6的单层网壳结构,用随机缺陷模态法可以得到较为可靠的稳定承载力.为此,建议对于大矢跨比网壳结构采用两种缺陷分布模态法进行稳定计算. 以凯威特_联方单层球面网壳结构为例,采用随机缺陷模态法进行了非线性稳定分析,并与一致缺陷模态法计算结果进行对比分析,得出以下主要结论: (1)随机缺陷模态法取空间样本数目n≥90计算得到的网壳结构稳定极限荷载精度和概率保证率较高. (2)对于大矢跨比单层网壳结构,采用一致缺陷模态法所得稳定极限荷载有可能不是最小值,应采用随机缺陷模态法加以验证. (3)当单层网壳结构的矢跨比小于或等于1/6时,两种初始缺陷分布方法计算出的稳定极限荷载接近. [1]PAPADOPOUIOS V,PAPADRAKAKIS M.A computationally efficient method for the buckling analysis of shells with stochastic imperfections [J].Computational Mechanics,2009,43 (5):688-700. [2]ROUDSARI M T,GORDINI M.Random imperfection effect on reliability of space structures with different supports [J].Structural Engineering and Mechanics,2015,55 (3):461-472. [3]SHEIDAII M R,GORDINI M.Effect of random distribution of member length imperfection on collapse behavior and reliability of flat double-layer grid space structures [J].Advances in Structural Engineering,2015,18 (9):1475-1483. [4]BRUNO L,SASSONE M,VENUTI F.Effects of the equiva-lent geometric nodal imperfections on the stability of single layer grid shells [J].Engineering Structures,2016,112 (1):184-199. [5]QI Lin,ZHANG Xian-min,HUO Hai-feng.Design bearing capacity of the initial imperfect lattice shell [J].Advances in Structural Engineering,2016,19 (1):14-22. [6]赵海,徐亚洲,白国良.随机缺陷场对网壳结构性能影响的研究 [J].空间结构,2011,17(4):24-26. ZHAO Hai,XU Ya-zhou,BAI Guo-liang.Influence of stochastic imperfection field on performance of latticed shell structures [J].Spatial Structures,2011,17(4):24-26. [7]刘慧娟,罗永峰,杨绿峰,等.单层网壳结构稳定性分析的随机缺陷模态迭加法 [J].同济大学学报(自然科学版),2012,40(9):1295-1299. LIU Hui-juan,LUO Yong-feng,YANG Lv-feng,et al.Stochastic imperfection mode superposition method for stabi-lity analysis of single-layer lattice domes [J].Journal of Tongji University(Natual Science),2012,40(9):1295-1299. [8]卢家森,张其林.球面网壳最不利几何缺陷的凸集和概率模型 [J].工程力学,2013,30(7):100-104. LU Jia-sen,ZHANG Qi-lin.Convex and probabilistic mo-dels of uncertainties in initial geometric imperfections of latticed shells [J].Engineering Mechanics,2013,30(7):100-104. [9]刘学春,张爱林.基于随机缺陷理论的大跨度预应力弦支穹顶结构非线性整体稳定分析 [J].北京工业大学学报,2013,39(8):1201-1205. LIU Xue-chun,ZHANG Ai-lin.Integral stability analysis of large-span prestressed suspend-dome based on defect probabilistic theory [J].Journal of Beijing University of Technology,2013,39(8):1201-1205. [10]陈世英,张素娟,李青,等.初始几何缺陷对网壳截面优化结果影响研究 [J].力学与实践,2015,37(6):709-712. CHEN Shi-ying,ZHANG Su-juan,LI Qing,et al.The influence of initial geometric imperfection on the section optimization result of reticulated shell [J].Mechanics in Engineering,2015,37(6):709-712. [11]蔡健,贺盛,姜正荣,等.单层网壳结构稳定性分析方法研究 [J].工程力学,2015,32(7):103-110. CAI Jian,HE Sheng,JIANG Zheng-rong,et al.Investigation on stability analysis method of single layer latticed shells [J].Engineering Mechanics,2015,32(7):103-110. [12]唐敢,黎德琳,赵才其,等.空间结构初始几何缺陷分布规律的实测数据及统计参数 [J].建筑结构,2008,38(2):74-78. TANG Gan,LI De-lin,ZHAO Cai-qi,et al.Statistical regulation and parameter study on initial geometrical imperfections of spatial structures based on measured data [J].Building Structure,2008,38(2):74-78. [13]范峰,曹正罡,马会环,等.网壳结构弹塑性稳定性[M].北京:科学出版社,2015. [14]JGJ 7—2010,空间网格结构技术规程 [S]. [15]亓民勇,董金新.基于卡方拟合优度检验的序列等概性测试组 [J].计算机工程与设计,2012,33(5):1758-1759. QI Min-yong,DONG Jin-xin.Test suit for sequence equal probability based on chi square goodness of fit test [J].Computer Engineering and Design,2012,33(5):1758-1759. [16]唐敢,郭小明,练兰英,等.网壳结构稳定性分析的改进随机缺陷法智能控制 [J].南京航空航天大学学报,2012,44(3):410-414. TANG Gan,GUO Xiao-ming,LIAN Lan-ying,et al.Intelligent control of advanced stochastic imperfections me-thod for stability analysis of lattice shells [J].Journal of Nanjing University of Aeronautics & Astronautics,2012,44(3):410-414. [17]魏德敏,张科龙,姜正荣.某大跨单层球面网壳结构的非线性屈曲研究 [J].空间结构,2014,20(1):41-44. WEI De-min,ZHANG Ke-long,JIANG Zheng-rong.Research of nonlinear buckling for one large-span single-layer spherical latticed shell [J].Spatial Structures,2014,20(1):41-44. Supported by the Open Subject of the State Key Laboratory of Subtropical Building Science(2012ZC23) A Probe into Nonlinear Stability of Single-Layer Reticulated Shells by Means of Random Imperfection Modal Method WEIDe-minTUJia-ming (School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,Guangdong,China) The nonlinear stability of Kiewitt-Lamella single-layer reticulated shells is analyzed by means of random imperfection modal method,and the stable ultimate load of the reticulated shell structure,which is affected by both the spatial sample number of random defect and the rise-span ratio,is investigated. Then,a comparison of calculated results is made between random imperfection modal method and consistent imperfection modal method. The results show that (1) the spatial sample number of random defect should be not less than 90 for the stability analysis of structures via statistical method; (2) for the reticulated shell structure with large rise-span ratio,the probabilistic reliability to calculate the critical load via consistent imperfection modal method is rather low,so that it is nece-ssary to verify the critical load with the help of random imperfection modal method; and (3) when the rise-span ratio of a single-layer reticulated shell is less than 1/6,the calculated stable bearing capacities obtained by the two above-mentioned initial defect distribution methods are nearly equal. single-layer reticulated shell; random imperfection modal method; consistent imperfection modal me-thod; nonlinear analysis; rise-span ratio; stable ultimate load 1000-565X(2016)07-0083-07 2015-12-07 亚热带建筑科学国家重点实验室开放课题(2012ZC23) 魏德敏(1955-),女,教授,主要从事大跨空间结构方面的研究.E-mail:dmwei@scut.edu.cn TU 393.3doi: 10.3969/j.issn.1000-565X.2016.07.013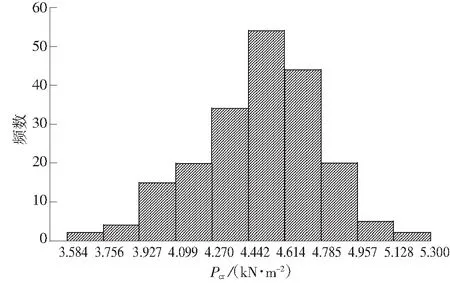
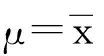
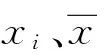
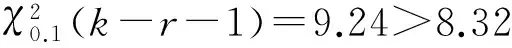
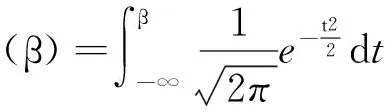
3 参数分析



4 与一致缺陷模态法结果对比
5 结语

