指数函数CORDIC算法的FPGA定点化技术*
唐文明 刘桂雄
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
指数函数CORDIC算法的FPGA定点化技术*
唐文明刘桂雄
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
CORDIC算法广泛应用于多种超越函数求值,但其通用迭代算法难以用现场可编程门阵列(FPGA)计算宽范围定义域指数函数求解.为此,文中提出一种FPGA定点化技术,通过收敛域扩张与迭代结构优化实现CORDIC算法的指数函数求值器.首先,应用区间压缩方法实现指数函数CORDIC算法的收敛域扩张;其次,对CORDIC算法的迭代结构进行优化;最后,通过对指数函数求值器的仿真分析与FPGA实现,采用15级流水线结构,用双曲系统CORDIC算法求解指数函数,实现指数函数CORDIC算法的收敛域扩张.仿真与实验表明:相比于通用CORDIC算法,所提算法的迭代模式节省约1/3硬件资源,少至2个乘法单元,使收敛域由[-1.118 2,1.118 2] 扩张到[-6,6],运算结果相对误差达10-3.
CORDIC算法;指数函数;区间压缩;收敛域;迭代结构优化;现场可编程门阵列
指数函数是一种常见超越函数,广泛应用于各种数值计算中.目前指数求值方法主要有查表法、泰勒展开式法、多项式逼近法等[1-5];其中查表法随结果精度提高或输入值范围增大,需大量存储单元;泰勒展开式法需要复杂求导运算以及大量的乘、除法器,速度慢、效率低;多项式逼近法算法非常复杂,且精度非常有限.基于坐标旋转数字计算 (CORDIC) 方法的基本思想是通过一系列与运算基数相关的固定角度不断旋转来逼近所需的旋转角度,其算法结构主要涉及移位、加法运算,便于硬件实现,但求解指数函数时因收敛域窄而导致定点化实现精度低[6-7].鉴于现场可编程门阵列(FPGA)灵活的时序、组合电路运行模式,可快速并行定点化信号处理等特点[8-9],文中研究了一种定点化指数函数双曲系统CORDIC算法的FPGA实现技术,并对输入值进行区间压缩以实现指数函数CORDIC算法的收敛域扩张[10],使CORDIC算法可以指数函数运算;并将该算法应用于超声相控阵的时间校准增益(Time Corrected Gain,TCG)功能[11-12].
1 双曲坐标指数函数CORDIC算法的求解机理与收敛范围
CORDIC算法作为一种通用迭代算法,通过控制向量可在线性坐标系、圆坐标系和双曲坐标系下旋转和定向操作,但指数计算通常在双曲坐标系下完成[13-15].图1为双曲函数坐标旋转模型图,图中,θ为射线OVn、双曲线和x轴围成面积的2倍(弧度值),φ为射线OV1、双曲线和x轴围成面积的2倍,分别对应阴影部分面积的2倍,双曲函数x2-y2=C2上点V1(x1,y1)沿着上半轴曲线移动到点Vn(xn,yn),可表示为
(1)

图1 双曲函数坐标旋转模型
将θ分解成一系列θi(i=1,2,…,n)累加和形式,即
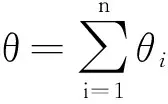
令θi满足条件tanhθi=2-i,式(1)可表示为
(2)
其中旋转方向因子为di,校模因子K为
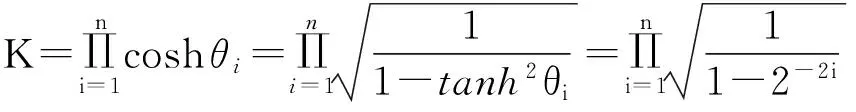
当C=0时,双曲线x2-y2=C2最终退化为直线,暂不考虑K,则迭代递推关系为
(3)
式中:i=1,2,3,…,n.
为满足迭代序列收敛,迭代序列i的取值从第4项开始,当i=kn(kn=3kn-1+1,k1=4,n∈Z+)时,重复此次迭代,即i=1,2,3,4,4,…,13,13,…,40,40….
经过n次旋转后,有
(4)
若取初值x1=y1=1/K,z1=θ,则有
xn+1=yn+1=coshz1+sinhz1=eθ.这就是双曲坐标指数函数CORDIC算法的求解机理.
但根据式(3)可得双曲线坐标CORDIC算法的收敛范围为

其中,θmax为所有旋转面积(弧度)和,即该算法收敛的最大弧度值.
由于θ的收敛范围较小,因而实际应用意义受到限制,必须对收敛域进行扩张处理.
2 指数CORDIC算法的收敛域扩张方法
为解决双曲线坐标CORDIC算法收敛范围狭小的问题,需通过对收敛域进行扩展以满足指数函数求解算法的通用性.
2.1区间压缩方法实现指数CORDIC算法收敛域扩张
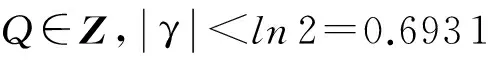
eθ=eQln 2+γ=2Qeγ,
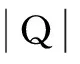
2.2整数Q值和γ值定点化值处理
若Q表示θ与ln 2相除得到商的整数部分,γ表示θ与ln 2相除得到的余数部分,则小数部分R表示为γ与ln 2相除得到的商,即:Q=[θ/ln 2],γ=θMOD ln 2,R=γ/ln 2,则
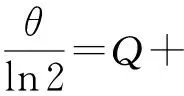
FPGA通常实现定点数运算,故在求解Q、γ过程中必须进行定点化处理,扩大65 536 (216)倍实现定点化,把除法运算转换成乘法运算,有:

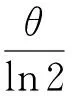
(5)
式中,Q∈Z.
2.3Q值与定点化γ值的FPGA求解
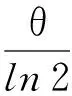
Q=H10
(6)
即H10为整数部分Q值.
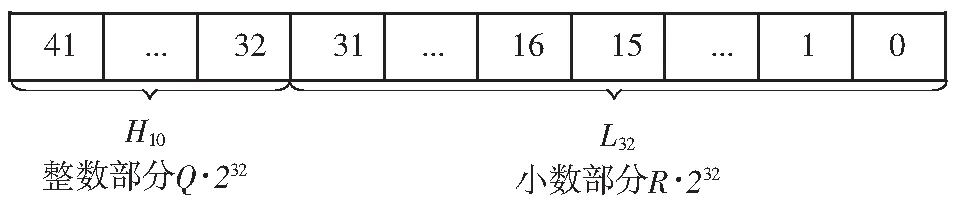
图2 [θ·2216·(216/ln 2)]对应二进制数位结构
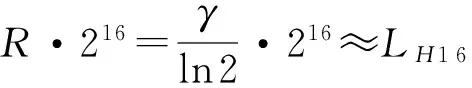
216·216·γ=(ln 2·216)·LH16≈45 426·LH16
(7)
则[45 426·LH16]位宽为32 bit.图3给出对应的二进制数位结构,用H16表示bit[31:16]共16 bit,如是有:
216·γ=H16
(8)
即H16为余数部分γ的定点化值(扩大216倍).

图3 [45 426·LH16]对应二进制数位结构
根据式(5)-(8),基于FPGA定点化技术实现该算法,整数Q、γ定点化值求解原理框图如图4所示.由图4可见,只用到两个乘法器,即可实现整数Q、定点化余数γ值求解,实现定点化区间压缩,达到收敛域扩张的效果.

图4 整数Q和定点化余数γ值求解原理框图
Fig.4The principle diagram of calculating solution for integerQand fixed-point remainderγ
3 指数CORDIC算法的FPGA实现与应用
3.1指数CORDIC算法的FPGA实现
图5为指数CORDIC算法求解指数函数的流水线结构图,由于坐标xn、yn的初值与迭代模式相同,可以合成为一个迭代通道,省掉坐标yn的迭代过程,这时式(3)转化为
(9)
式中:i=1,2,3,…,n.
式(9)中xi、zi迭代运算物理意义:算法只需用到两条迭代数据链,可省去一条迭代数据链,即仅对角度zi与坐标xi进行迭代,这种方式在硬件实现上可节省约1/3硬件资源[16],极大提高了FPGA处理算法的实时性.
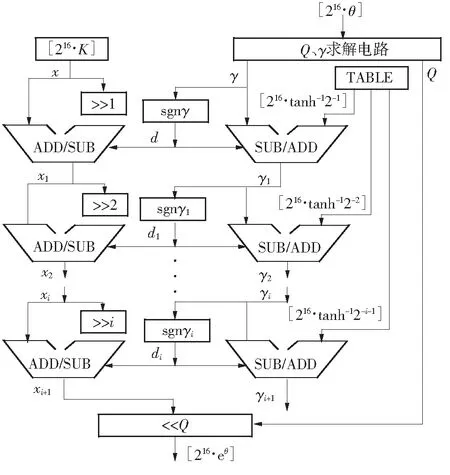
图5 指数CORDIC算法求解指数函数的流水线结构图
Fig.5Pipeline structure diagram of exponential CORDIC algorithm solving the exponential function
图6所示为指数函数CORDIC算法的Modelsim(FPGA编程语言行为级仿真软件)仿真结果.采用15级流水线CORDIC算法结构,输入定点化参数[θ·216],其中θ∈[-6,6].图中变量theta对应θ值、exp对应eθ指数函数值,横坐标对应仿真时间(10 ns仿真时钟周期),纵坐标为幅度,比如:此时垂直光标线位置对应的输入值θ=1,输出值为e1≈ 2.718 23,与理论值2.718 28相比,相对误差为
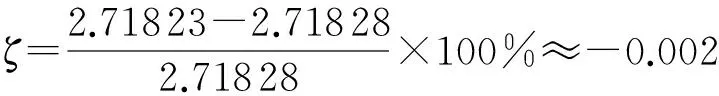
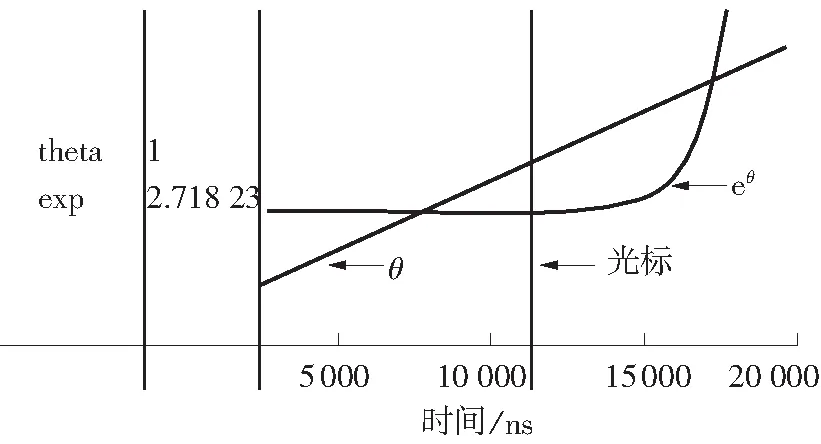
图6 指数CORDIC算法的Modelsim仿真结果
Fig.6The results of exponential CORDIC algorithm by Modelsim simulation
收敛域θ∈[-6,6]时各输入值的FPGA运算结果如表1所示.
表1收敛域θ∈[-6,6]时各输入值的 FPGA运算结果
Table 1Results of FPGA operation when input partial values of the convergence regionθ∈[-6,6]

θeθ·65536eθ实际值eθ理论值相对误差/%-61620.002470.00248-0.275-54410.006730.00674-0.131-412000.018310.01832-0.028-332620.049770.04979-0.026-288690.135330.13534-0.004-1241090.367870.36788-0.001-0655361.000001.000000.000-11781422.718232.71828-0.002-24842487.389047.389060.000-3131617620.0832520.08554-0.011-4357788854.5942454.59815-0.007-59726464148.41406148.413160.001-626436608403.39063403.42879-0.009
可以看出,相对误差最大为-0.275%(扩大小数位),其相对误差达到10-3,可满足很多实际工程上精度的要求,在实际应用中可进一步扩大定点化倍数以减小相对误差.
与工程上FPGA实现指数函数算法的经典查表法性能对比,可通过算法精度与所耗内存资源量进行分析.若精度提高L位(扩大10L倍),应用查表法,对应内存资源(单位:bit)为
LRAM=10L
(10)
而使用文中指数CORDIC算法求解器时,增加的二进制数位宽(单位:bit)为
LB=L·log210≈3.321 9L
(11)
因文中为15级流水线两个迭代通道,故增加的存储单元bit数约为
(12)
由式(10)、(12)可得,基于FPGA指数求值器算法精度与消耗内存量增加关系,文中CORDIC算法与经典查表法的性能对比关系如表2所示.
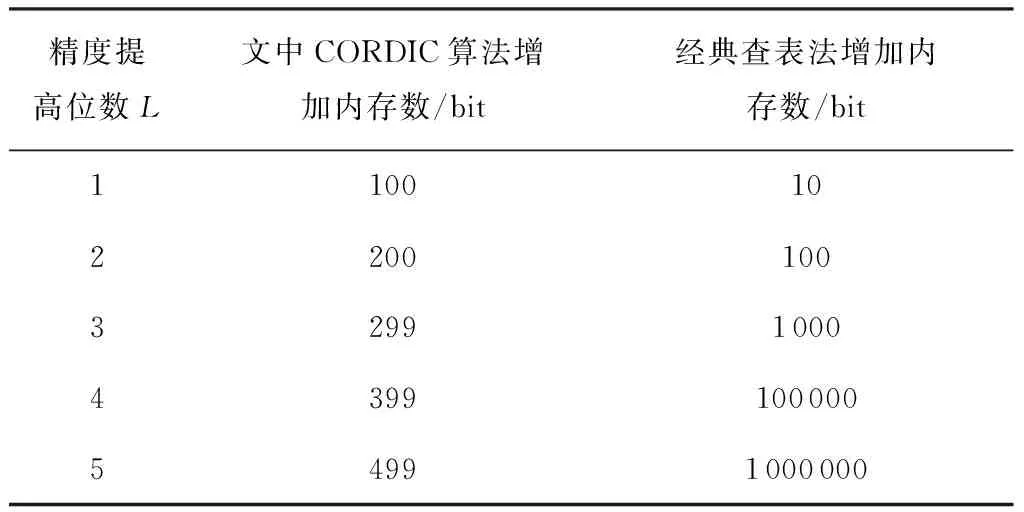
表2CORDIC、查表法指数求值器(L=1,2,…,5)内存增加量
Table 2The number of increasing memory of exponential eva-luator through CORDIC and look-up table (L=1,2,…,5)
精度提高位数L文中CORDIC算法增加内存数/bit经典查表法增加内存数/bit110010220010032991000439910000054991000000
由表2可以看出,随着精度增加,指数求解器所耗内存资源文中CORDIC算法成线性增加,而经典查表法成指数增加,体现了文中CORDIC算法的优越性.
3.2指数CORDIC算法在TCG技术中的应用
超声相控阵仪器为了对不同探测深度(时刻)的缺陷回波有统一的评判当量,使得相同尺寸缺陷回波幅度与其在材料中的深度无关,对不同深度的反射回波幅度进行增益dB补偿,将所有的深度补偿值连成一条曲线,即TCG曲线.算法上是通过增益控制器实现dB到放大倍数A的转换:
dB=20lgA⟺A=e(dB·ln10)/20
(13)
使用广州多浦乐电子科技有限公司生产的超声相控阵仪器(PA2000)对B型相控阵标准测试模块中深度5、10 mm的φ1 mm平底孔进行检测实验,通过式(13)做出一系列增益补偿曲线,其TCG技术增益补偿效果如图7所示.图中横坐标:左半部分A扫图表示回波幅度相对百分比 (单位:%)、右半部分B扫图表示水平扫查位移(单位:mm),纵坐标表示垂直扫查深度(单位:mm),图中B扫光标位置对应A扫图,曲线列举了5个点的增益补偿连线(先用标准工件检测,把不同深度相同直径缺陷回波增益调到相同的回波高度,再记录下每个深度缺陷所额外增加的增益(ΔdB)值,用相应ΔdB值对不同位置回波进行增益补偿形成TCG曲线,对缺陷进行评判),可以看出经TCG曲线补偿后不同深度平底孔几乎相同(图中标签①、②所示),为缺陷评判提供了有力保证.
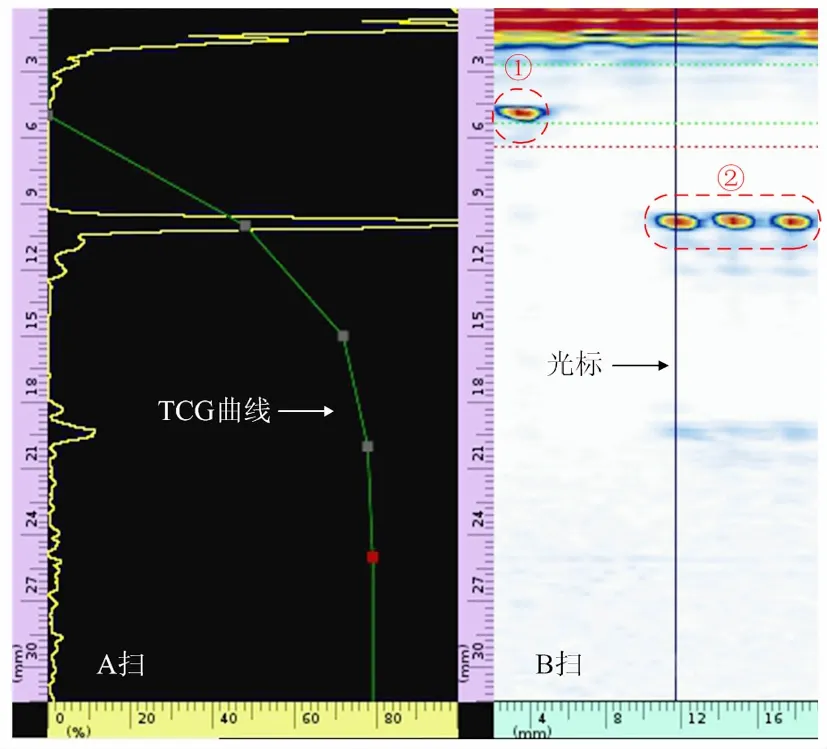
图7 TCG技术增益补偿效果
4 结语
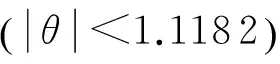
在收敛域扩张方法上,根据输入值θ与ln2相除的结果,通过分析商、整数、小数、余数部分的关系,最终根据关系式θ=Q·ln2+γ,把eθ的计算等效转化为eγ(|γ| 算法只需用到两条迭代数据链,可省去一条迭代数据链,即仅对角度zi与坐标xi进行迭代,这种方式在硬件实现上可以节省约1/3硬件资源,大幅度提高FPGA处理算法实时性. 通过15级的迭代流水线,对CORDIC算法指数求解器进行FPGA实现与ModelSim仿真,求解值相对误差达到了10-3,能满足很多实际工程要求,在超声相控的TCG功能中具有重要实用价值. [1] LAKSHMI B,DHAR A S.CORDIC architectures:a survey [J].VLSI Design,2010,2010:1-19. [2]SIDAHOAO N,CONSTANTINIDES G A,CHEUNG P Y.Architectures for function evaluation on FPGAs [C]∥Proceedings of IEEE International Symposium on Circuits and Systems.Bangkok:IEEE,2003:804-807. [3]YLOSTALO J.Function approximation using polynomials [J].IEEE Signal Processing Magazine,2006,23(5):99-102. [4]MULLER J M.A few results on table-based methods [J].Reliable Computing,1999,5(3):279-288. [5]NAGAYAMA S,SASAO T.Programmable numerical function generators based on quadratic approximation [C]∥Proceedings of Asia South Pacific Design Automation Conference.Yokohama:IEEE,2006:378-383. [6]LAKSHMI B,DHAR A S.VLSI architecture for parallel radix-4 CORDIC [J].Microprocessors and Microsystems,2013,37(1):79-86. [7]沃焱,徐角.精确的快速极坐标谐波变换 [J].华南理工大学学报(自然科学版),2012,40(4):23-29. WO Yan,XU Jiao.Accurate and fast harmonic transform of polar coordinates [J].Journal of South China University of Technology(Natural Science Edition),2012,40(4):23-29. [8]牟胜梅,李兆刚.一种面向FPGA的指/对数函数求值算法 [J].计算机工程与应用,2011,47(33):59-61. MOU Sheng-mei,LI Zhao-gang.FPGA-oriented evaluation algorithm for exponential and logarithm functions [J].Compu-ter Engineering and Applications,2011,47(33):59-61. [9]牟胜梅,杨晓东.eθ的CORDIC 迭代初值选取策略及其硬件实现 [J].计算机工程与应用,2007,43(6):79-80. MOU Sheng-mei,YANG Xiao-dong.Policy of choosing initial values for CORDIC iteration and its effect on hardware implementation of exponential function [J].Compu-ter Engineering and Applications,2007,43(6):79-80. [10]何晓华,谢建精.基于扩张收敛域CORDIC的指数变换器设计 [J].计算机仿真,2010,27(7):365-368. HE Xiao-hua,XIE Jian-jing.Design of exponential function generator based on CORDIC algorithm with expanded range of convergence [J].Computer Simulation,2010,27(7):365-368. [11]VASJANOV A,BARZDENAS V.Design of a time-gain-compensation amplifier for ultrasonic echo signal processing [C]∥Electrical,Electronic and Information Sciences.Vilnius:IEEE,2015:1-6. [12]庞林花,文桂林.报废回收汽车零部件再利用的无损检测技术 [J].华南理工大学学报(自然科学版),2014,42 (11):55-62. PANG Lin-hua,WEN Gui-lin.A study on nondestructive testing technology for recycling of re-usable automotive parts [J].Journal of South China University of Techno-logy (Natural Science Edition),2014,42(11):55-62. [13]杨宇,毛志刚,来逢昌.一种改进的流水线CORDIC算法结构 [J].微处理机,2006(4):10-14. YANG Yu,MAO Zhi-gang,LAI Feng-chang.An improved pipeline structure for CORDIC [J].Icroprocessors,2006(4):10-14. [14]NASCIMENTO I,JARDIM R,MORGADO-Dias F.A new solution to the hyperbolic tangent implementation in hardware:polynomial modeling of the fractional exponential part [J].Neural Computing & Applications,2013,23(23):363-369. [15]苏诚,韩俊刚.一种对数求值器的硬件实现 [J].协议·算法及仿真,2013,26(10):7-10. SU Cheng,HAN Jun-gang.A hardware implement of the logarithmic evaluator [J].Electronic Sci & Tech,2013,26(10):7-10. [16]刘美娟,许建华,张超.基于CORDIC算法的对数放大器的FPGA实现 [J ].仪器仪表学,2008,29(4):328-331.LIU Mei-juan,XU Jian-hua,ZHANG Chao.Implementation of logarithmic amplifier in FPGA based on CORDIC algorithm [J].Chinese Journal of Scientific Instrument,2008,29(4):328-331. Supported by the National Key Foundation for Exploring Scientific Instrument(2013YQ230575) FPGA Fixed-Point Technology of Exponential Function Achieved by CORDIC Algorithm TANGWen-mingLIUGui-xiong (School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China) Although CORDIC algorithm has been widely used in various transcendental functions,its general iterative algorithm is inefficient in using FPGA (Field Programmable Gate Array) to solve the exponential function in a wide-range domain. In order to solve this problem,an FPGA fixed-point technology,which expands the convergence region and optimizes the iteration structure to implement CORDIC algorithm solver,is designed. In the investigation,firstly,range compression method is employed to realize the convergence domain expansion of exponential function achieved by CORDIC algorithm. Secondly,the iteration structure of CORDIC algorithm is optimized. Then,the exponential function achieved by CORDIC algorithm is analyzed in a simulative way and implemented in FPGA. Finally,a 15-grade pipeline structure as well as a hyperbolic method is used to implement the expansion in convergence domain of CORDIC algorithm. Simulated and experimental results show that,in comparison with the general CORDIC algorithm,the proposed algorithm saves about 1/3 hardware resources,uses only two DSP multiplexer units,expands the convergence domain from [-1.118 2,1.118 2] to [-6,6],and achieves a relative error low to 10-3. CORDIC algorithm; exponential function; range compression; convergence region; iteration structure optimization; field programmable gate array 1000-565X(2016)07-0009-06 2015-11-23 国家重大科学仪器设备开发专项(2013YQ230575);广州市科技计划项目(201509010008) 唐文明(1983-),男,博士生,主要从事无损检测与数字信号处理技术研究.E-mail:twm316@163.com TH 878.2doi: 10.3969/j.issn.1000-565X.2016.07.002

