中国潜在风力发电量的年际变化
王凌霄 鲁玺 刘术艳 林金泰,†
中国潜在风力发电量的年际变化
王凌霄1鲁玺2刘术艳3林金泰1,†
1. 北京大学物理学院大气与海洋科学系, 北京 100871; 2. 清华大学环境学院, 北京 100084; 3. Center for Satellite Applications and Research, National Oceanic and Atmospheric Administration, College Park, MD 20740; † 通信作者, E-mail: linjt@pku.edu.cn
结合观测资料和数值模拟结果, 基于GE 2.5 MW风机的功率曲线, 分析1982—2006年中国大陆陆地上潜在风电量的年际变化。结果表明, RegCM3模式风速、观测插值风速和两者平均风速对应的 25 年平均年潜在风电量分别为每年 25, 2.5和11 PWh, 均超过中国2030年预期电力需求的20% (2 PWh)。三者年潜在风电量的相对标准差分别为 3%, 8%和 5%, 相对极差分别为 15%, 33%和 23%, 年际变化较大。由于风电和电力需求的季节性不匹配以及风电较大的年际变化, 若仅依靠风电, 在夏季容易出现电力缺口, 意味着需要大量后备发电机组, 这将提升发电总成本, 降低风电减排效益。
风电量; 容量因子; 年际变化
与传统能源不同, 风力发电不依赖化石燃料的燃烧, 在风机运行期间没有温室气体排放, 因此风能被视为应对全球变暖的有效手段之一[1]。进入21世纪, 以风能为主的可再生能源在世界范围内迅速发展, 截至2013年末, 全球风电累积装机达到318.1 GW[2], 中国风电累积装机已达91.4 GW[2]。由于中国能源需求快速增长, 石油对外依存度较高[3], 加之气候变暖背景下巨大的减排压力, 因此发展风电对中国具有重要意义。
风速的多变导致风电具有复杂的时间变化性, 这是风电开发的挑战之一。瞬时的变化导致风电输出功率波动大、并网困难[4], 月际和年际的变化可能导致电力供给的缺口, 需要配置以火电和水电为主的大量备用机组[5], 这不仅造成发电总成本上涨, 而且可能削弱风电的减排效益。
文献中对风资源年际变化的研究, 以对近地面观测风速年际变化的分析为主。大量研究结果显示, 近50年来中国近地面风速存在逐年减小的趋势[6-10], 1990年后这种减小趋势有所减弱[10]。仅依赖气象观测资料分析风速或风能资源的年际变化存在一定的局限性[11], 包括观测高度与风机轮毂高度不匹配、气象站分布稀疏、易受城市化影响等。
基于中尺度模式分析风功率密度(正比于风速的三次方[12-13])的年际变化, 是研究风资源年际变化的另一种重要手段。Pryor等[14]和江滢等[15]利用包括RegCM3 (Regional Climate Model 3)在内的多个区域模式, 分别分析美国和中国 20 世纪后期的风功率密度分布。本研究也采用 RegCM3 模式。中尺度模式一般由全球模式或者再分析资料提供边界条件。再分析资料中近地面风速相对于观测资料差异较大[7,16-18], 中尺度模式 RegCM3 对中国近地面风速的模拟相对于观测资料偏高[19]。由于观测资料和中尺度数值模式各自的局限性, 在没有更高空间分辨率的数值模式资料的情况下, 将两者结合起来可能是一种较优的方案。
风速和风功率密度与风机输出功率之间存在复杂关系。由 GE 2.5 MW 风机功率曲线(图 1)可知, 风机的输出功率与风速之间不存在线性关系, 风机的输出功率与风功率密度之间也不存在线性关系。因此, 风速和风功率密度的年际变化不能直观地反映潜在风电量的年际变化。
目前, 广泛应用 CF 因子(capacity Factor, 一段时间内风机输出功率与额定功率之比)定量分析潜在风电量的大小[4,13,20-24], 研究的时间尺度通常为几个月到数年, 有关潜在风电量年际变化的研究较少。然而, 风机的生命周期通常在 20 年左右[25-26]。在风机生命周期尺度下, 分析潜在风电量的年际变化, 有助于电力系统对风力发电做出更稳健的规划, 也可以更精确地评估风电的减排效益。
本文结合地面观测资料和 RegCM3 数值模拟结果, 采用基于风机功率曲线的计算方法, 估算中国大陆陆地上 1982—2006 年间不同年份的潜在风电量, 在接近风机生命周期(20 年)和短期气候变化周期(30 年)[27]的时间尺度下, 分析潜在风电量的年际变化, 为更精确地评估风电经济效益和减排效益打下基础。
1 资料来源及研究方法
1.1 资料来源
1.1.1 风机资料
不同风机的功率曲线大致类似, 在数值上有所差异, 对风机的选择将在一定程度上影响对潜在风电量的估计。本文关注风电量的相对年际变化, 采用何种风机可能对此影响不大, 故假定采用 GE 2.5 MW风机, 其扇叶半径为50 m, 轮毂高度为100 m, 额定输出功率为 2.5 MW。在标准空气密度(1.225 kg/m3[13,24])下, 其功率曲线如图 1 所示, 其切入风速为 3.5 m/s, 切出风速为 25 m/s, 额定风速为 12.5 m/s。基于其功率曲线计算潜在风电量, 需 100 m高度的风速数据。此外, 许多研究将高度 100 m 左右作为分析风能资源的参考高度[4,13,22-23,28]。
1.1.2 气候模式资料
本研究采用的 RegCM3 模式数据[29]被许多研究者用于风能资源分析[14-15,19], 具有一定的模拟中国区域近地层风速变化的能力[15], 其水平分辨率为30 km × 30 km, 时间分辨率为3小时, 输出近地面10 m 高度及模式各高度层的风速。此外, 本研究基于 RegCM3 模式近地面不同高度层的风速以及幂律形式风廓线函数(其中是摩擦系数,是高度的风速,0是高度0的风速)[24,30], 插值得到100 m高度的风速。
1.1.3 观测资料
翻转课堂(flipped classroom,简称FC)是指通过借助现代教育技术手段预先录制授课视频来取代传统的课堂知识讲授,并在网络上进行共享,要求学生课前自主观看学习,然后利用课堂时间集中解决学生在观看视频时所产生的困惑和疑问,实现知识内化的一种教学形态[1]。翻转课堂最早起源于美国[2],自2011年起翻转课堂作为新时期教学模式的重大变革被逐步推广,近年来在我国的基础教育领域受到许多教育学者的重视,并开始在我国逐步推广[3]。
采用美国国家气候资料中心(NCDC)提供的近地面观测数据[31], 包括中国数百个观测站(图 2) 1982—2006 年的近地面 10 m 高度风速数据, 时间分辨率为3小时。依照RegCM3模式格点分布, 将观测数据格点化, 若同一格点有多个观测站, 则采用各站点的平均风速, 并筛选得到 275 个格点观测数据(筛选标准: 去除任一年份缺失的观测数据量达到 20%的格点, 去除观测与 RegCM3 模式 10 m 高度平均风速之比小于 0.25 或者大于 1.5 的格点)。
本研究采用的数据资料时间尺度长达 25 年, 超过常规风机的预期寿命20年, 接近30年的短期气候变化周期[27], 可以在风机生命周期和短期气候变化周期的时间尺度下, 分析中国潜在风电量的年际变化。
1.2 研究方法
1.2.1 观测插值风速的计算流程
首先, 依照 RegCM3 的 10 m 高度风速的水平空间分布, 将观测站的 10 m 高度风速反距离加权插值到中国大陆所有格点。具体做法是, 将观测值与 RegCM3 模式风速的比值反距离加权插值到所有格点, 再将其乘以RegCM模式风速。
然后, 基于工程实践中常用的幂律形式风廓线函数[24,30], 利用模式风速估算不同格点、不同时间的摩擦系数, 将水平插值的观测风速(10 m)垂直转化为 100 m 高度的风速。我们可获得的铁塔观测数据[32](图 3)表明, 在玉门铁塔观测站, 观测资料和RegCM3模式中, 100 m和10 m高度风速的垂直转化关系是相似的。至于真实大气中不同地点、不同时间的风速垂直转化关系, 有待基于更多铁塔数据的进一步研究。
综上所述, 在标准密度下的 100 m 高度格点化观测插值风速的计算流程(简称观测插值风速)如图 4 所示。
1.2.2 潜在风电量的计算方法
为了定量计算潜在风电量的大小, 采用基于风机功率曲线的计算方法, 将风速时间序列转化为风机的 CF 因子, 去除不适合开发风电的区域, 并减去由于风机相互影响所造成的能量损失, 计算得到任一格点潜在风电量的大小。计算公式如下:
PWE = Time × RP × CF × (Area ×
LUR × TD) × (1 − ELR) ,
PWE (potential wind electricity)为任一格点的潜在风电量, Time为时间长度, RP (rated power)为风机额定功率, CF 为 CF 因子, Area 为格点面积, LUR (land utilization rate)为可用于风电开发的土地利用率, TD (turbine density)为风机密度, ELR (energy loss rate)为能量损失率。
由于植被和地形等的限制, 部分区域不适宜开发风电。本文基于GLCNMO的精度为 1 km 的地表植被数据[33], 参考文献[13,18]的方法, 去除森林、冰雪、水体、城市、农田和沙漠地区以及海拔大于 3500 m 的高原地区。因为电力系统的不同, 本文未纳入台湾地区的资料。由于缺乏海上风速观测资料, 本文未对近海潜在风电量进行分析。
风机尾流相互影响造成的能量损失[13,34]是影响潜在风电量大小的重要因素之一, 因此需量化分析其影响程度。本文采用文献[13,30]中的简化计算方法, 假设风机呈矩形阵列分布, 其间距均为 7 倍扇叶直径(对应 TD = 2 km−2), 风机尾流相互影响导致的能量损失低于 20%。本文假定这样的能量损失是 20% (ELR = 20%), 由此计算出的潜在风电量的数值相对保守。此外, 本文没有考虑电力传输过程中的能量损失, 因此所得结果是中国大陆并网前的潜在风电量。
本文对潜在风电量的计算过程相对简单, 引入了一些不确定性。就不确定性的来源而言, 第一, 观测资料和数值模拟结果对区域风速的代表性有限; 第二, 风机的功率曲线存在一定的不确定性, 约为 6%~8%[24]; 第三, 本文简单量化风机尾流相互影响造成的能量损失[13,30], 与真实情况之间存在差异。对可能引入的不确定性因素做进一步分析, 将获得对潜在风电量的年际变化的更多认知。
2 中国大陆CF因子的分布和潜在风电量的年际变化
2.1 中国大陆CF因子的分布情况
CF 因子的分布情况是计算中国年潜在风电量的基础, 也是分析潜在风电量年际变化的基础。基于观测插值得出的 100 m 风速数据以及 RegCM3模式 100 m 风速数据, 能够计算得到两组 CF 因子分布。此外, 本文引入观测插值与RegCM3模式的100 m高度平均风速, 得到另一组CF因子分布。
从图 5 可知, 3 组数据对应的 1982—2006 年 CF因子平均值的区域分布具有相似的特征: 风能资源最丰富的地区位于内蒙古、新疆北部、东北地区和东南沿海地区, 区域分布与中国气象局第四次风能资源普查的结果[28]相似。3 组数据的 CF 因子有一定的差异, RegCM3模式对应的CF因子最大, 观测插值对应的 CF 因子最小, 观测插值和RegCM3 模式平均风速对应的CF因子位于两者之间。
3组数据对应的CF因子的年际相对标准差(CF因子相对标准差 = CF 因子标准差 / CF 因子平均值)在分布上具有相似的规律: 风能资源丰富的地区, CF因子的年际相对标准差较小, 适宜风电开发; 反之, 风能资源较贫瘠的地区, CF 因子的年际相对标准差较大, 可能影响风电开发的经济效益。关于CF 因子年际相对标准差, 观测插值风速对应的数值最大, RegCM3 模式对应的数值最小, 观测插值和 RegCM3 模式平均风速对应的数值也位于两者之间。
根据前面的讨论, 观测站资料可能低估中国近地面风速[11], 而中尺度模式RegCM3对中国近地面风速的模拟相对于观测风速偏高[19]。观测插值与RegCM3模式的平均风速所对应的CF因子位于两者之间, 其年际变化幅度也位于两者之间, 其风能资源的区域分布与中国气象局第四次风能资源普查的结果[28]较为接近, 因此本文主要基于此平均风速展开讨论。
2.2 不同CF阈值对应的潜在风电量
倘若只在CF因子大于一定阈值的区域开发风电, 潜在风电量的数值将会随着 CF 阈值的提升而减少。Lu 等[13]分析了全世界潜在风电量的数值与CF 阈值的关系, Brower[22]和Elliott 等[23]分析了美国潜在的风电装机功率与 CF 阈值的关系。本文分析中国年潜在风电量与CF阈值的关系。
图 6 显示利用 3 组数据(RegCM3模式风速、观测插值风速、两者平均风速)分别得到的年潜在风电量随25年平均CF阈值的变化, 区域的上下界反映在不同 CF 阈值下 1982—2006 年间年潜在风电量的最大值与最小值。由图 6 可知, 对于年潜在风电量的估计而言, 基于 RegCM3 模式的估计值较大, 较为激进; 基于观测插值的估计值较小, 较为保守; 基于观测插值与RegCM3模式平均风速的估计值居中。
当CF阈值变化时, 3组数据对应的年潜在风电量的变化特征相似。从图 6 可知, 在 CF 阈值低于10%时, 风力发电量随着 CF 阈值增加呈缓慢下降趋势; 当 CF 阈值大于某一界限时, 风力发电量随着 CF 阈值增加而快速下降, 直至下降速度趋缓, 年潜在风电量趋于零。
2013 年, 中国并网风电设备平均利用小时数为2080 小时[35], 对应的 CF 因子约为 24%。另一方面, 中国气象局第四次风能资源普查设定的阈值之一是风功率密度大于等于 400 W/m2, 对应的年平均风速约为 7 m/s[28]。该平均风速对应GE 2.5 MW风机的 CF 因子约为 26%。作为分析的参考值, 本研究将 CF阈值定为25%。
设定 CF 阈值为 25%, 基于观测插值与RegCM3模式的平均风速这组数据, 中国大陆年潜在风电量的多年平均值约为每年11 PWh。中国2012年的电力消耗约为5 PWh, 2030年的电力消耗预计约为11 PWh[36], 均与之相差不大。全球风能理事会预测: 到 2030 年, 风力发电可以提供全球 20%的电力需求[37]。从本研究的计算结果来看, 中国的风能资源足以满足 2030 年 20%的电力需求(约 2 PWh)。
表1列举不同研究者用以估算中国潜在风电量的大致方法和得出的结论。在 100 m 左右高度, 本研究对中国潜在风电量的估计值为每年 11 PWh, 低于 Lu 等[13]的估计值(每年 39 PWh), 高于中国气象局估计值(每年 5 PWh)[28]。本研究基于 RegCM3 模式的估计值(每年 25 PWh)比较接近 Lu 等[13]基于 GEOS-5 DAS 再分析资料的估计值。本研究的结果与文献[28]的结果差异较大, 可能的原因如下: 一方面, 文献[28]中只估计风电的潜在开发量(潜在装机功率), 而为了与其他研究对比, 本研究将其乘以风电设备平均利用小时数以估计潜在风电量, 这样的估算方法可能存在误差; 另一方面, 在更为充足的地理资料基础上, 文献[28]中剔除不可开发风能区域的设定更加严格, 因此对风能资源的估计可能更为保守。在估计年潜在风电量大小的基础上, 本研究进一步分析其年际变化, 对前人的研究有所推进。
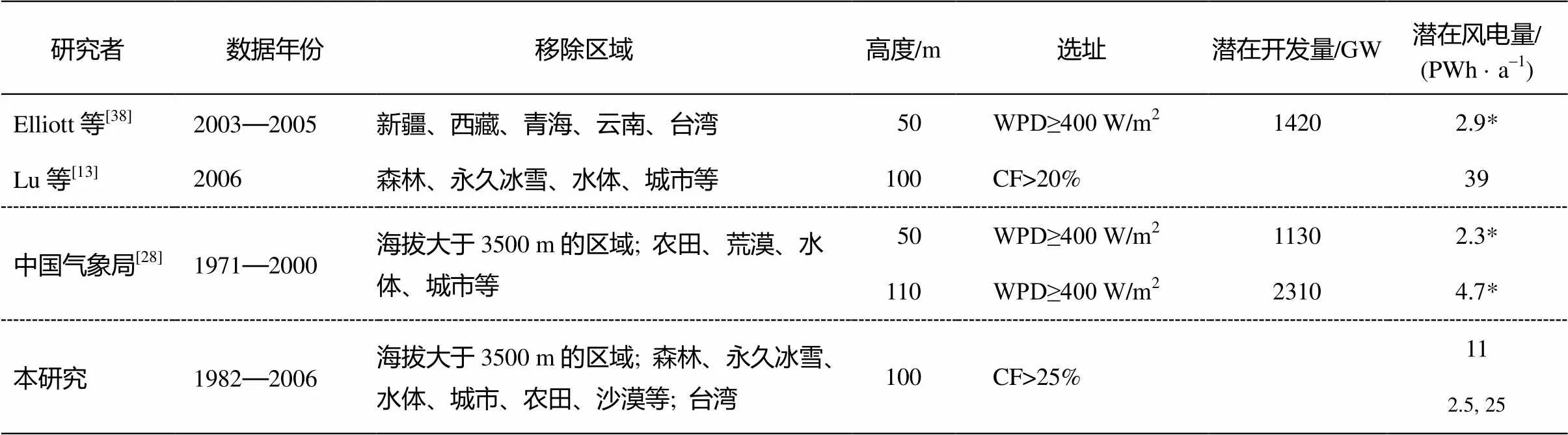
表1 不同研究对中国年潜在风电量的估计
注: *由潜在开发量(潜在装机功率)以及 2013 年中国并网风电设备平均利用小时数(2080 小时)相乘所得的估计值; WPD 为风功率密度(wind power density); 2.5和25 PWh/a分别为基于观测插值风速和基于RegCM3模式风速算得的潜在风电量; 基于两者平均风速算得的潜在风电量为11 PWh/a。
2.3 中国潜在风电量的年际变化
大量研究表明, 近50年来, 中国近地面观测风速呈现逐年减小的趋势[6-10], 但是这一减少趋势在1990 年以后有所减弱[10]。本研究的时间尺度为1982—2006 年, 在此期间潜在风电量的年际变化是研究的重点。
假设选址条件为 25 年(1982—2006 年)平均的CF因子大于25%, 可以计算3组数据(RegCM3模式风速、观测插值风速、两者平均风速)各年份潜在风电量。从图 7 可知, 3 组数据具有相似的年际变化特征: 1987年潜在风电量最大, 1990年以后的年际变化幅度相对于 1990 年之前较小。RegCM3风速、观测插值风速、两者平均风速对应的多年平均年潜在风电量分别是每年 25, 2.5 和 11 PWh, 三者的年潜在风电量差异较大。究其主要原因, 可能是RegCM3 模式 10 m 风速相对于观测值偏高[19]。年潜在风电量的相对标准差分别是3%, 8%和5%, 相对极差(最大值和最小值之差与平均值之比)分别为15%, 33%和23%, 年际变化较大。
对于观测插值与 RegCM3 模式的平均风速这组数据, 假设将 CF 阈值分别取20%~35%的一系列数值, 可得到不同 CF 区间对总的潜在风电量的贡献情况(图 8(a))。采用 20%~35%的任一 CF 阈值, 年潜在风电量的相对标准差均在 5%左右, 相对极差均在 23%左右, 同比变化范围在−10%~13%之间, 在某些连续年份可能出现较大的突变, 这样的突变在电力规划中需要妥善应对。本文选取的不同 CF阈值对应风资源富饶度不同的区域, 它们的潜在风电量的年际变化特征基本上一致。
假若依据各年份的 CF 因子进行选址, 其结果可能出现显著差异。基于每年的 CF 因子分布, 按CF 阈值进行选址, 可以算得每年的潜在风电量(图8(b)), 因此图 8(b)中同一 CF 阈值对应的每年风电场选址不同。假设 CF 阈值为 25%, 年潜在风电量的相对标准差约为 15%, 相对极差约为 62%。相对于图 8(a), 图 8(b)中年潜在风电量的年际变化显著加大。许多研究者利用单年或者数年的数据分析风能资源[13,38], 他们对年潜在风电量的估计和基于多年资料的估计可能存在较大差异, 且无法分析风机生命周期内潜在风电量的年际变化。
2.4 月潜在风电量的年际变化
风能资源具有季节性特征, 月潜在风电量亦存在一定的年际变化。假设 25 年平均 CF 阈值设为25%, 计算得到 1982—2006 每月潜在风电量(乘以10%)如图9所示。对 25 年中同一月份的潜在风电量而言, 其年际相对标准差约为 13%, 相对极差在40%~70%之间。相对于年潜在风电量的年际变化, 月潜在风电量的年际变化更为显著。
由于潜在风电量和电力需求的季节性变化, 若仅依靠风力发电, 在某些月份可能出现电力缺口。假如用 1982—2006 年平均年潜在风电量的 10%供应 2012 年电力需求的20%, 在 7—9 月容易出现电力缺口, 8 月电力缺口在极端年份可达电力需求的约 50%。因此, 用风电供电需要配置较大规模的后备发电机组[5], 以填补风力发电的电力缺口。假如用火电作为风电的后备发电机组, 意味着风电代替的火力发电机组中, 有一半需定期维护, 作为后备,这样, 将提升风力发电的总成本, 降低风力发电减排效益。
就季节性而言, 风电和水电具有良好的季节互补性[39-40], 在不同季节风电和水电可互为后备发电机组, 由此可控制总成本, 提高减排效益。从图 9可知, 25 年平均的月潜在风力发电量与 2012 年的月水力发电量具有良好的互补性, 但因为月风电量和月水电量都具有较大的年际变化, 在某些年份这样的互补性可能不显著, 需进一步研究。
3 总结
风速的多变导致风电具有复杂的时间变化性, 对风电开发提出挑战。在接近风机生命周期(20 年)和短期气候变化周期(30 年)的时间尺度下, 本文分析了中国大陆陆地上潜在风电量的年际变化, 对于量化风电的经济效益和减排效益具有重要意义。
根据本文的简化计算, 中国风资源较丰富, 年际变化较大。RegCM3 模式风速、观测插值风速和两者平均风速对应的 1982—2006 年平均年潜在风电量分别是25, 2.5和11 PWh, 均超过中国2030年预期电力需求的 20% (2 PWh)。年潜在风电量的相对标准差分别是 3%, 8%和 5%, 相对极差分别为15%, 33%和23%, 年际变化较大。
本文研究结果显示, 对于观测插值与 RegCM3模式的平均风速这组数据, 将 CF 阈值分别取 20%~ 35%范围内的一系列数值, 年潜在风电量的相对标准差均在 5%左右, 相对极差均在 23%左右, 同比变化范围在−10%~13%之间。在电力规划中需妥善应对这样的年际变化。
同时, 研究结果显示, 风电与电力需求的季节变化具有不匹配性。如果仅依靠风力发电, 在夏季容易出现电力缺口, 加上风电较大的年际变化, 在平均潜在风电量最小的 8 月, 电力缺口在极端年份可达电力需求量的约 50%。因此, 用风电供电需配置较大规模的后备发电机组, 将提升发电的总成本, 降低风电减排效益。
本研究简化计算各年份的潜在风电量, 所依赖的数据资料较少, 而且简化计算方法可能存在一些缺陷, 计算结果可能存在一些不确定性。今后的研究需对可能引入的不确定性因素进行细致分析, 以获得对潜在风电量年际变化的进一步认知。
致谢 对在本文撰稿过程中给予帮助的北京大学物理学院大气与海洋科学系张宏升教授和燕莹莹、倪睿婧、刘梦瑶同学, 以及北京大学医学部程雅琳同学, 致以诚挚的谢意。
参考文献
[1]Ming Z, Kun Z, Jun D. Overall review of China’s wind power industry: status quo, existing problems and perspective for future development. Renewable & Sustainable Energy Reviews, 2013, 24: 379‒386
[2]全球风能理事会. 2013全球风电统计. 风能, 2014(2): 60-63
[3]赵俊平, 马小涛. 我国石油贸易现状分析及其改善对策. 黑龙江对外经贸, 2011(1): 23‒25
[4]Liu Y, Xiao L Y, Wang H F, et al. Investigation on the spatiotemporal complementarity of wind energy re-sources in China. Science China-Technological Scien-ces, 2012, 55(3): 725‒734
[5]Li X, Hubacek K, Siu Y L. Wind power in China-Dream or reality?. Energy, 2012, 37(1): 51‒60
[6]李艳, 王元, 汤剑平. 中国近地层风能资源的时空变化特征. 南京大学学报: 自然科学版, 2007, 43(3): 280‒291
[7]Chen L, Li D, Pryor S. Wind speed trends over China: quantifying the magnitude and assessing causality. International Journal of Climatology, 2013, 33(11): 2579–2590
[8]Lin C G, Yang K, Qin J, et al. Observed coherent trends of surface and upper-air wind speed over China since 1960. Journal Of Climate, 2013, 26(9): 2891‒ 2903
[9]Jiang Y, Luo Y, Zhao Z, et al. Changes in wind speed over China during 1956–2004. Theoretical and App-lied Climatology, 2010, 99(3): 421‒430
[10]Guo H, Xu M, Hu Q. Changes in near-surface wind speed in China: 1969–2005. International Journal of Climatology, 2011, 31(3): 349‒358
[11]李泽椿, 朱蓉, 何晓凤, 等. 风能资源评估技术方法研究. 气象学报, 2007, 65(5): 708‒717
[12]姚国平, 余岳峰, 王志征. 如东沿海地区风速数据分析及风力发电量计算. 电力自动化设备, 2004, 24(4): 12‒14
[13]Lu X, Mcelroy M B, Kiviluoma J. Global potential for wind-generated electricity. Proc Natl Acad Sci U S A, 2009, 106(27): 10933‒10938
[14]Pryor S C, Barthelmie R J. Assessing climate change impacts on the near-term stability of the wind energy resource over the United States. Proc Natl Acad Sci U S A, 2011, 108(20): 8167‒8171
[15]江滢, 罗勇, 赵宗慈. 中国未来风功率密度变化预估. 资源科学, 2010, 32(4): 640‒649
[16]Pryor S C, Barthelmie R J, Young D T, et al. Wind speed trends over the contiguous United States. Journal of Geophysical Research-Atmospheres, 2009, 114(D14): 1159‒1171
[17]Mcvicar T R, Van Niel T G, Li L T, et al. Wind speed climatology and trends for Australia, 1975–2006: capturing the stilling phenomenon and comparison with near-surface reanalysis output. Geophysical Research Letters, 2008, 35(20): L20403
[18]Vautard R, Cattiaux J, Yiou P, et al. Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nature Geoscience, 2010, 3(11): 756‒761
[19]Jiang Y, Luo Y, Zhao Z C, et al. Projections of wind changes for 21st century in China by three regional climate models. Chinese Geographical Science, 2010, 20(3): 226‒235
[20]Mcelroy M B, Lu X, Nielsen C P, et al. Potential for wind-generated electricity in China. Science, 2009, 325: 1378‒80
[21]Sinden G. Characteristics of the UK wind resource: long-term patterns and relationship to electricity demand. Energy Policy, 2007, 35(1): 112‒127
[22]Brower M. New US wind energy potential estimates-background and explanation of changes from prior estimates. Albany: AWS Truepower [EB/OL]. (2010‒05) [2015‒06]. https://www.awstruepower.com/knowledge- center/technical-papers/
[23]Elliott D, Schwartz M, Haymes S, et al. 80 and 100 meter wind energy resource potential for the United States [EB/OL]. Proceedings of Windpower 2010. Albany: NREL. (2010‒05) [2015‒06]. http://www. nrel.gov/wind/pdfs/48036.pdf
[24]Kwon S D. Uncertainty analysis of wind energy potential assessment. General Information, 2010, 87 (3): 856‒865
[25]Fleck B, Huot M. Comparative life-cycle assessment of a small wind turbine for residential off-grid use. Renewable Energy, 2009, 34(12): 2688‒2696
[26]Martinez E, Sanz F, Pellegrini S, et al. Life cycle assessment of a multi-megawatt wind turbine. Rene-wable Energy, 2009, 34(3): 667‒673
[27]World Meteorological Organization. Calculation of Monthly and Annual 30-Year Standard Normals. WCDP-No. 10, WMO-TD/No. 341, 1989
[28]肖子牛, 朱蓉, 宋丽莉, 等. 中国风能资源评估(2009). 北京: 气象出版社, 2010
[29]Liu S, Gao W, Min X U, et al. China summer precipitation simulations using an optimal ensemble of cumulus schemes. Frontiers of Earth Science in China, 2009, 3(2): 248‒257
[30]Masters G M. Renewable and efficient electric power systems. Hoboken: John Wiley & Sons, 2004
[31]Smith A, Lott N, Vose R. The Integrated surface database: recent developments and partnerships. Bull Amer Meteor Soc, 2011, 92(6): 704‒708
[32]何玉斐, 张宏升, 刘明星, 等. 戈壁下垫面空气动力学参数确定的再研究. 北京大学学报: 自然科学版, 2009, 45(3): 439‒443
[33]Tateishi R, Uriyangqai B, Al-Bilbisi H, et al. Production of global land cover data — GLCNMO. International Journal of Digital Earth, 2011, 4(1): 22‒49
[34]Barthelmie R J, Pryor S C, Frandsen S T, et al. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. Journal of Atmospheric and Oceanic Technology, 2010, 27(8): 1302‒1317
[35]国家能源局. 2013 年全国 6000 千瓦及以上电厂发电设备平均利用小时情况[EB/OL]. (2014‒02‒10) [2015‒06]. http://www.nea.gov.cn/2014-02/10/c_1331 03830.htm
[36]单葆国, 韩新阳, 谭显东, 等. 中国“十三五”及中长期电力需求研究. 中国电力, 2015, 48(1): 6‒10
[37]Global Wind Energy Council. Global wind energy outlook 2010 [EB/OL]. (2010‒10) [2015‒06]. http://www.gwec.net/wp-content/uploads/2012/06/GWEO-2010-fi nal.pdf
[38]Elliott D, Schwartz M, Scott G, et al. Wind energy resource atlas of southeast China. Golden: N ational Renewable Energy Lab [EB/OL]. (2002‒12) [2015‒06]. http://www.nrel.gov/docs/fy03osti/33101.pdf
[39]孙春顺, 王耀南, 李欣然. 水电‒风电系统联合运行研究. 太阳能学报, 2009, 30(2): 232‒236
[40]尚志娟, 周晖, 王天华. 带有储能装置的风电与水电互补系统的研究. 电力系统保护与控制, 2012, 40(2): 99‒105
Interannual Variability of Wind Energy Potential in China
WANG Lingxiao1, LU Xi2, LIU Shuyan3, LIN Jintai1,†
1. Department of Atmospheric and Oceanic Sciences, School of Physics, Peking University, Beijing 100871; 2. School of Environment, Tsinghua University, Beijing 100084; 3. Center for Satellite Applications and Research, National Oceanic and Atmospheric Administration, College Park, MD 20740; † Corresponding author, E-mail: linjt@pku.edu.cn
Based on the combined data of observations, RegCM3 model and the power curve of GE 2.5 MW wind turbine, the interannual variability of wind energy potential (WEP) over 1982-2006 in China is analyzed. It is calculated that the WEP of RegCM3 wind, observation-adjusted wind and their mean wind is 25, 2.5 and 11 PWh/a, all more than 20% of China’s expected electricity demand in 2030 (2 PWh/a). Their relative standard deviations of yearly WEP are about 3%, 8% and 5%, and their relative ranges of yearly WEP are 15%, 33% and 23%. Because of the seasonal variation of wind energy and electricity demand, power deficit could occur in summer if relying on wind energy only, resulting in a need of huge backup capacity that reduces the economic benefit and emission benefit.
wind energy potential (WEP); capacity factor; interannual variability
10.13209/j.0479-8023.2015.147
TK81
2015-04-21;
2015-05-26; 网络出版日期: 2016-03-18
国家自然科学基金(41175127, 41422502)和国家重点基础研究发展计划(2014CB441303)资助

