深读文本题尽其用

摘要：教材习题是教材的重要组成部分，充分挖掘和把握教材习题中的有限资源，可以提高学生的练习效率，提升教学质量。教材习题的研用策略主要有：沟通联系，理清习题编排的意图与层次；换位思考，预测学生解题的特点与难点；整合重组，提高课堂练习的效率与效度；拓展延伸，增加思维训练的宽度与深度。在教学中要根据学生的实际情况和课堂时间的长短进行灵活处理，才能让教材习题的作用发挥到极致。

关键词：教材习题；研读；沟通联系；换位思考；练习效率

中图分类号：G623.5 文献标识码：A 文章编号：1674-120X（2016）23-0040-03 收稿日期：2016-04-13

课题项目：本文系福建省莆田市城厢区2014—2015年度教育科学规划课题“小学数学课堂练习有效性的实践研究”（CXKT201409）研究成果之一。

作者简介：林雪芬，福建省莆田市城厢区逸夫实验小学教导主任，小学高级教师，本科。

现行的新课标修订教材的配套练习题量繁多、题型丰富，供教师选择和利用的空间很大。因此，我们没有必要舍近求远，大量翻阅和选用课外习题，而应该加强对教材习题的深入研读，充分挖掘和把握习题中的有利资源，做到“题”尽其用，以提高学生的练习效率，提升教学质量。

一、沟通联系，理清习题编排的意图与层次

人教版数学教材的编排一般是新授内容（例题）与随堂练习（做一做）1∶1搭配，再加一些单元综合练习和复习中的练习。随堂练习的编排目的明确，我们要侧重于研读单元综合练习中的习题。在研读时，要沟通习题与例题、单元综合练习与随堂练习之间的联系，理清习题编排的意图和层次，才能用好教材的每一道习题。

例如，人教版修订教材五年级上册“小数乘整数”，教材安排了两个例题和一个综合练习（如图1）。

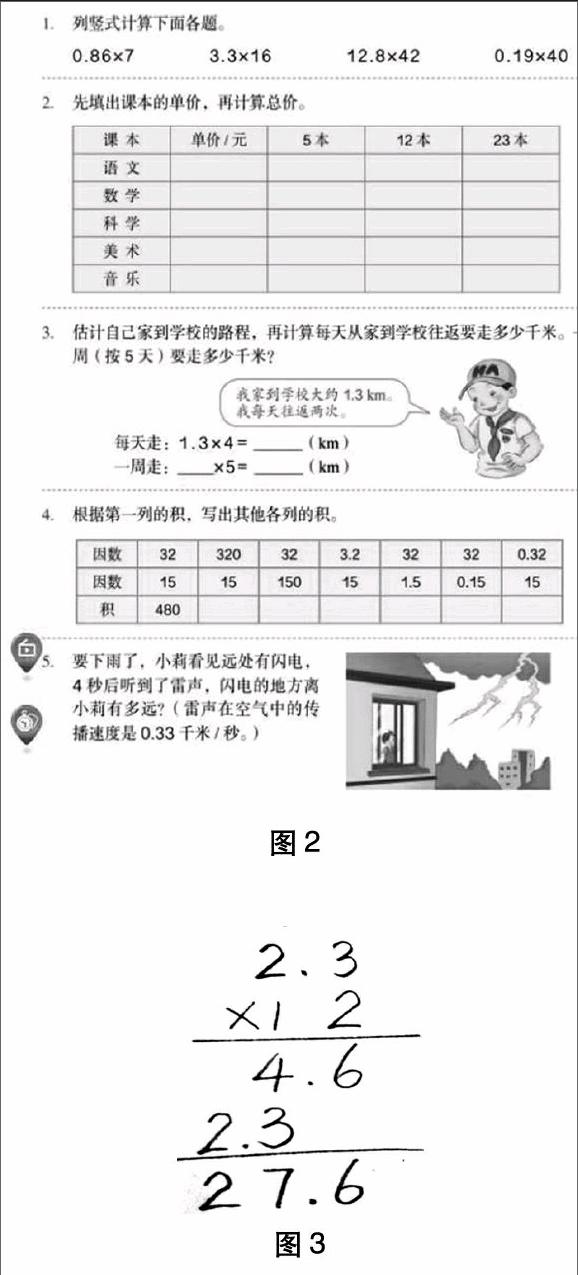
首先，我们来分析一下习题与例题的关系。例1下面有两道“做一做”的习题，都是组合具体的量计算小数乘整数，其中第1题与例1题型一样，属于巩固练习，第2题有所拓展，学生可算出具体的钱数再判断，也可通过估算来解决。例2下面配3道“做一做”的练习，第1题通过对比整数乘整数和小数乘整数，明确了二者之间的联系与区别，培养学生的迁移能力。第2题是小数点的专项训练，订正时可让学生观察比较四道试题，找出它们之间的异同点，联系积的变化规律，帮助学生理解。第3题是计算技能的训练，其中第1小题与例2相似，第3小题是一个因数中间有0的乘法，第2、第4小题第二个因数是两位数，是对例题的拓展，算理是一样的，只是难度有所提高。综合练习（练习一）有5道习题（如图2），基本是匹配例2的教学内容。其中第1题是基础练习，用于巩固小数乘整数的运算技能。第4题是专项练习，应用因数的变化引起积的变化的规律进行计算，既巩固了积的小数点的练习，又沟通了新旧知识的联系，为下面学习“小数乘小数”做好了铺垫。第2、第3、第5题是应用小数乘整数的计算技能解决实际问题的练习，其中第2题利用新学期开始的契机，让学生查阅新书的单价，再计算，增加了练习的趣味性，也复习了“单价×数量=总价”的数量关系。第3题先估计自己家到学校的路程，再计算每天、每周的上下学路程，将数学知识与学生的生活紧密联系，提高了学生对知识的应用能力，也使他们加深了对1千米长度的具体感受。第5题渗透了“先看到闪电后听到雷声”的科学常识，在激趣的同时复习了“速度×时间=路程”的数量关系。再来看单元综合练习与随堂练习之间的关系。练习一的第1题与例2下面“做一做”的第3题相似，只是增加练习竖式的写法。第2题与例1下面“做一做”的第1题类型相似。第4题与例2下面“做一做”的第2题相似。

通过以上的分析，这部分内容建议分两课时完成，第1课时完成例1和例2及相应“做一做”内容的教学，把例2的方法融入例1的教学当中，例1原题是3.5×3，增加3.5×6和3.5×14，让学生尝试独立计算，再交流，比较异同，这样更加完整地呈现小数乘整数的几种情况，对算理的教学一气呵成。第2课时将练习一单独上一节综合练习课，为了提高课堂练习效率，可将第1题和第2题布置学生课前完成，在课堂上选一些错例进行分析交流，再将例1下面“做一做”的第2题放在第2课时作为练习一第2题的拓展题。

二、换位思考，预测学生解题的特点与难点

换位思考是指教师在研读习题时，要站在学生的角度来体验和思考解题过程，简而言之就是教师要将教材中的习题都做一遍，在做的过程中预测学生的解题特点与难点，体验其思考方法，从而更加准确地处理和运用每一道习题。

例如，上面的“小数乘整数”，学生在完成例2下面“做一做”第3题中的2.3×12时，个别学生会出现计算过程中使用小数点的现象（如图3），这是因为两道例题都是小数乘一位整数，学生的经验是每次乘完后点小数点，由此而产生的负迁移现象。教师在课前换位思考时，要揣摩学生的解题思路和特点，才能做到胸有成竹、得心应手。因此，在设计教学与练习时，可将这种类型的习题提前到例题的变式练习中，让学生尽早暴露错误，及时纠正，避免错误的思维定式扎根，这样也就发挥了习题的最大效益。

三、整合重组，提高课堂练习的效率与效度

教材习题是学生学习的重要资源，如果教师不进行适当的处理和加工，原汁原味、按部就班地呈现给学生练习，就会辜负习题的品质和编者的心血。况且对于课时相对紧张的数学学科来说，也是不允许的。因此，我们在研读习题、明确习题的编排意图后，要对习题进行必要的整合重组，或改变习题的呈现方式，或调整习题的练习顺序，或整合类型相似的习题等，以此提高课堂练习的效率和效度。

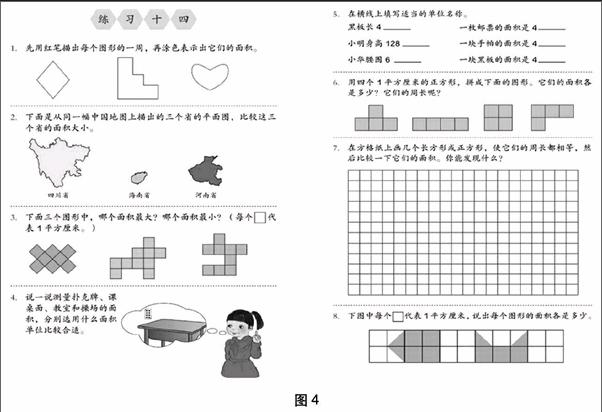
例如，人教版修订教材三年级下册“面积和面积单位”的单元综合练习（如图4），本组习题一共有8道，第1题通过描与涂的活动，

让学生感悟周长与面积的区别。第2题，让学生体会不规则图形也有面积，并且可以通过直接观察判断出面积的大小。第3题和第8题是通过数格子的方法比较面积的大小，渗透图形面积的大小与它所含面积单位的个数有关，与图形的形状无关，同时为下面学习长方形、正方形面积计算做准备，第8题还增加了两个半格转化成1格的方法，渗透等积变形思想。第4题是面积单位的应用，体会多个面积单位存在的价值，加深对三个常用面积单位的直观表象。第5题在第4题的基础上增加了长度单位的选择和应用，让学生进一步区分两种单位的本质。第6、第7题是周长与面积的对比练习，思维难度高，同时也渗透了变与不变的数学思想。

基于以上的分析，可如此处理：首先，第2题可前移至新授环节，作为认识面积及用观察法比较面积大小的一种类型。第3题和第8题属于同类题，且与前面例2下面的“做一做”极为相似，可以整合起来，把两道题连起来练习，节约时间，提高效率。第4题和第5题可以重组成一道题练习。第6题和第7题可进行对比练习，引导学生分析比较，体会面积相同的的图形周长不一定相同；周长相同的图形，面积不一定相同。这两道题要留给学生充足时间与空间，让他们自主发现，感悟规律，积累一定的学习经验。特别是第7题，让学生独立画周长相等的长方形和正方形，学生可能无从下笔，可建议让学生先画正方形，算出周长，再画与它周长相等的长方形，或者直接补充“周长为12格长”，这样，练习的目标更明确，练习也更有效度。

四、拓展延伸，增加思维训练的宽度与深度

教材中的每一道习题的编排都有其特定的功能，但教材是固定不变的，而学生是千变万化的，如何让相同的教材适用于不同班级、不同水平的学生呢？我们要抓住学生个体的差异，适时、适当地对教材习题加以拓展，提升思维训练的宽度和深度，满足不同层次学生的需求。拓展的方法有改变信息、增加问题、错中追问、逆向提问、改编类比，等等。

比如，“小数乘整数”随堂练习中的第2题，“40元买7个够吗？”当 学生想到用6.4×7算出具体的钱数进行比较时，教师肯定学生的想法后，可追问：有没有更简单的办法？学生在教师的启发下容易想到用估算的策略，一个风筝超过6元，7个风筝就超过42元，所以40元不够。此时教师可改变条件，将40元改为50元，引导学生进一步思考，一个风筝不到7元，7个风筝肯定不到49元，所以50元足够了。通过这样的拓展，培养学生思维的灵活性，拓展训练的宽度。

再比如，人教版修订教材五年级上册“小数除法”整理和复习配套综合练习中的第4题（如图5），看似简单，实则是易混易错题。问题一反常理，不是求速度，而是求跑1km所用的时间，学生在解题时既要认真审题，读出题中隐藏的信息，又要理清题目中的数量关系，有一定的难度。练习时可采用改编类比的方法，将问题改为：①刘大伯平均每分钟跑多少千米？②刘大伯跑1千米平均需要几分钟？③李大伯平均1分钟跑多少千米？结合题目中的问题，对比训练，有效培养学生的审题能力和思考能力。像这样对教材习题做适当的拓展延伸，在尽量短的时间内达到尽可能大的练习的宽度和深度，是提高课堂效率的一种有效策略。

倾力于教材习题的深入研究，是实现数学学科有效教学的必经之路，每一道习题的运用没有固定的模式，我们要根据学生的实际情况和课堂时间的长短进行灵活处理，才能让教材习题的作用发挥到极致。

参考文献：

朱德江.数学教师的练习运用力——“教学力”研修的内容与策略之七.小学数学教育，2015，（5）.

徐国裕.小学数学教材研读与教学.福州：福建教育出版社，2015.