降水量和温度对植被覆盖指数影响的空间非平稳性特征——以新疆伊犁河谷地区为例

冯金杰，张辉国，胡锡健*，师庆东，祖拜代·木依布拉

1 新疆大学数学与系统科学学院，乌鲁木齐 830046 2 新疆大学干旱生态环境研究所，乌鲁木齐 830046 3 新疆绿洲生态重点实验室，乌鲁木齐 830046



降水量和温度对植被覆盖指数影响的空间非平稳性特征
——以新疆伊犁河谷地区为例

冯金杰1，张辉国1，胡锡健1*，师庆东2，祖拜代·木依布拉2

1 新疆大学数学与系统科学学院，乌鲁木齐 830046 2 新疆大学干旱生态环境研究所，乌鲁木齐 830046 3 新疆绿洲生态重点实验室，乌鲁木齐 830046

多变量空间相关分析多基于时间序列数据，对数据时长与统计要求严格，空间非平稳性特征分析可以利用单期数据分析多变量之间的相关性。通过空间变系数回归模型分析了2006年和2011年的新疆伊犁地区降水量和温度对植被覆盖度指数影响的空间变化特征， 利用局部线性地理加权回归(GWR)方法估计得到了回归系数曲面，揭示出变量间相互影响的空间异质性，同时利用线性回归最小二乘估计进行了对比。结果表明：(1) 空间变系数回归模型可以用于变量间的空间相关分析；(2) 局部线性GWR估计方法明显优于线性回归最小二乘估计；(3)拟合结果表明，伊犁地区降水量和温度对植被覆盖指数的影响具有显著的空间非平稳性特征；(4)模型估计误差是降水、气温之外的地形、地貌及人类活动等多种因素造成的，需进一步研究。方法可为具有空间非平稳性特征变量间空间相关性分析以及植被覆盖指数的空间模拟分布提供思路和方法。

伊犁地区；空间变系数回归模型；局部线性GWR；植被覆盖指数；降水量； 温度

植被受气候、地形地貌及人类活动的影响在空间上具有差异性分布[1-3]，定位定量分析某一区域植被覆盖变化特征及驱动因素对区域生态环境保护有着十分重要的意义。温度与降水量是影响区域植被分布格局和覆盖变化的关键因子[4-6]。前期植被覆盖变化与气温、降水量的相关性研究中，多采用时间序列分析，这需要一定时间段的数据积累及尺度的一致性等统计要求。孙红雨等[7]采用时间序列方法，并结合同期的降水量和温度数据，对中国植被覆盖变化与气候因子进行相关性分析。李震等[8]利用1982年到2000年的数据采用差分法、斜率变化和主成分分析3种方法，研究了中国西北地区NDVI变化与温度和降水的关系。师庆东等[9]采用分区分海拔的方法对FVC影像进行分类，定量分析了1982年到2000年的新疆植被覆盖的变化情况并利用气温、降雨、地貌等因素进行了植被景观分类[3]。王智等[10-11]采用分区+海拔分类方法，对新疆各区分别做植被覆盖度与年均降水量、年均气温在长时间序列上的相关性分析。刘芳等[12]采用像元尺度的线性回归方法和相关系数法分析了伊犁河谷草地植被NDVI变化及其降水敏感性的特征。

上述研究多利用线性回归模型研究降水量或温度对植被覆盖指数的平均影响强度，这种方法需要多期数据的积累，受时间序列数据时序样本数量限制，研究结果的准确性受到限制。 实际上，植被覆盖度的空间特征与气温和降水有着直接联系，在每一个时间段中都具有这种空间相关性。本文利用单期植被覆盖指数、降水量和温度选择空间变系数模型，在Gauss核函数下用局部线性GWR估计方法进行拟合，用交叉确认法确定光滑参数h的值，采用三阶矩χ2逼近方法计算检验植被覆盖指数的空间非平稳性。同时在线性回归模型下用最小二乘估计方法进行拟合，把两种拟合结果与实测值进行对比分析，为检验算法的稳定性，以新疆伊犁地区2006、2011年两期数据验证，以该地区实际植被覆盖指数验证模型正确性与准确度，最终证明在只有单期降水量和温度数据支持的情况下，可以利用空间非平稳性特征分析方法对植被覆盖进行模拟，这为植被覆盖变化提供一种新的不受时间序列影响的计算方法。

1　研究区域概况及数据来源

1.1研究区域

研究区为伊犁哈萨克自治州，中国天山山脉西部，三面环山，“三山两盆两谷”组成该区域的主要地貌单元。地处80°9′42″—91°01′45″E，40°14′16″—49°10′45″N，属于温带大陆性气候和高山气候，年平均气温10.4℃，年日照时数2870h。年降水量417.6mm，山区达600mm，是新疆最湿润的地区。

图1　伊犁地区区域分布图Fig.1　The regional distribution graph of Yili area

1.2数据与数据处理

植被覆盖指数(FVC)[9]是从植被归一化指数 (NDVI)中推算出来的反映植被覆盖度的指数，它是反应某一区域环境好坏的重要指标，同时也能反映该区域生态环境的状况。本文所用遥感数据取自马里兰大学全球总量监测和模拟研究组发布的8km×8km分变率、15d最大值合成NOAA/AVHRR 的NDVI的2006和2011年数据集[9,13]，利用研究区边界矢量图切割生成研究的相关变量图。根据Guman[14]和Zeng等[15]提供的计算方法，将GMMS NDVI数据推算为FVC指数。

气温与降水量本文采用的数据由新疆大学干旱生态环境研究所提供，该数据的算法考虑了新疆地区气象站点稀疏，利用纬度、地形(DEM)等多种影响降水与气温的因子，通过多元回归与地形调节，复二次径向基函数计算获得[10-11]。对伊犁地区进行网格化后共产生了835个点，而在每个点处都有与其对应的植被覆盖指数、年均降水量和年均温度的值。

图2和图3分别为2006、2011年的年均降水量等值线图，伊犁地区位于新疆天山西部，北、东、南三面环山，只有西面敞开，从西而来的湿润气流在西部形成较多降水；中部平原地区受山地影响降水减少，而东部地区随海拔升高降水量增大。图4、图5表明伊犁中部平原地区随海拔升高年均温度降低，其中伊犁河、特克斯河等流域两岸的平均气温都高于其它地区，该地区温度主要受到地形(DEM)的影响。图6、图7为2006、2011年植被覆盖度图，显示了天山山脉、察汗乌逊山、依连哈比尔尕山以及伊犁河两岸的区域植被覆盖度较低，而其它区域都非常高，基本为纯植被覆盖，植被主要有荒漠、草原、草甸、森林和隐域植被类型[16]。从2006与2011年的相对数据分析，植被覆盖指数总的趋势基本一致，局部地区有变化，例如：2011与2006年相比昭苏县与特克斯县交界处且邻近巩留县的区域植被有所退化，而尼勒克县东部邻近依连哈比尔尕山的区域植被有所改善。伊犁地区降水、气温和植被覆盖指数分布具有显著的空间差异性。总体上，伊犁地区降水充沛和温度适宜的区域植被覆盖指数比较高，进而说明了降水量和温度都是影响植被覆盖变化的主要自然因子。

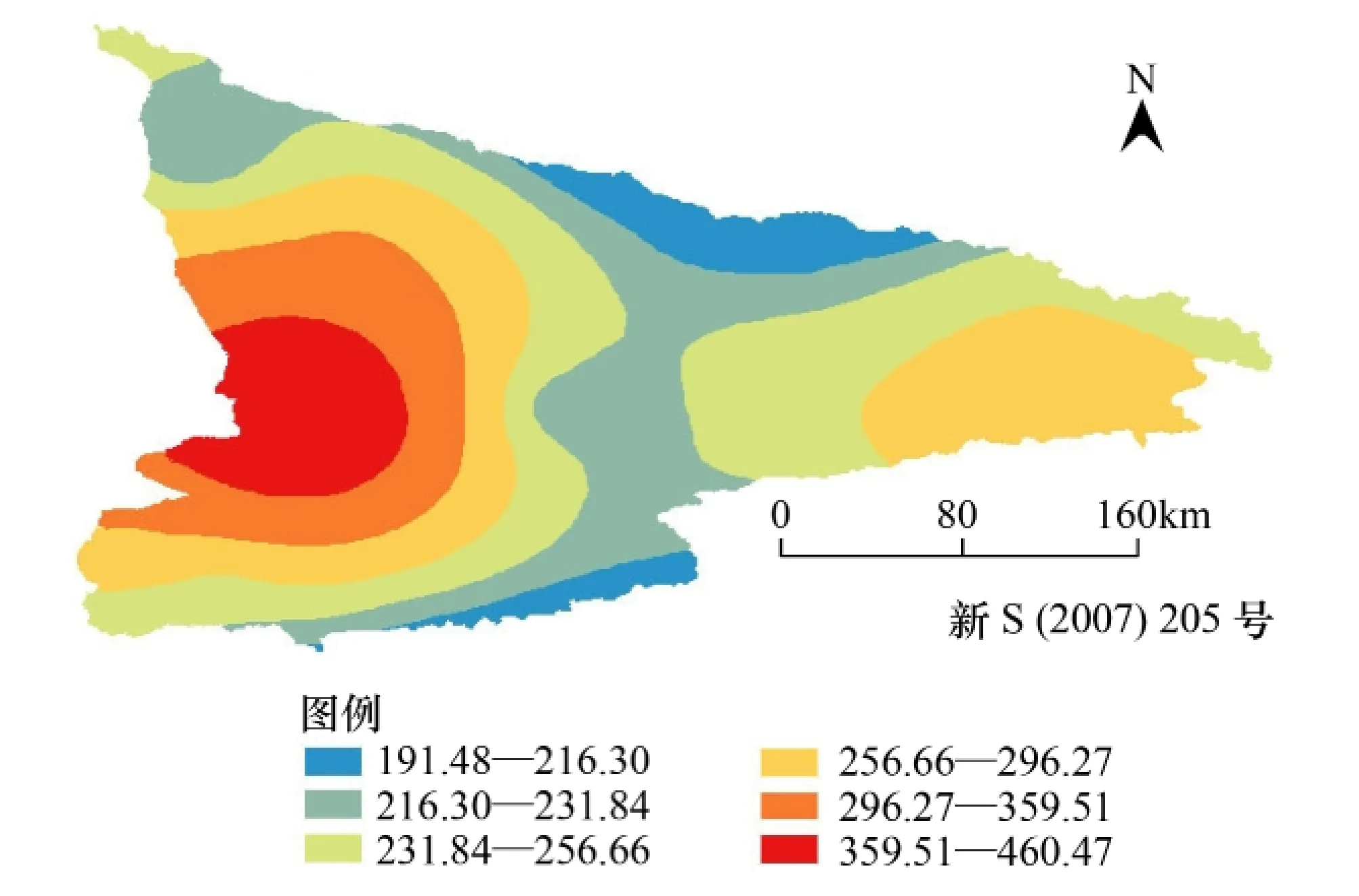
图2　2006实测降水量计算的年均降水量等值线图Fig.2　The contour map of average annual precipitation calculated by the measured precipitation of 2006

图3　2011实测降水量计算的年均降水量等值线图Fig.3　The contour map of average annual precipitation calculated by the measured precipitation of 2011

图4　2006实测温度计算的年均温度等值线图Fig.4　The contour map of average annual temperature calculated by the measured temperature of 2006

图5　2011实测温度计算的年均温度等值线图Fig.5　The contour map of average annual temperature calculated by the measured temperature of 2011

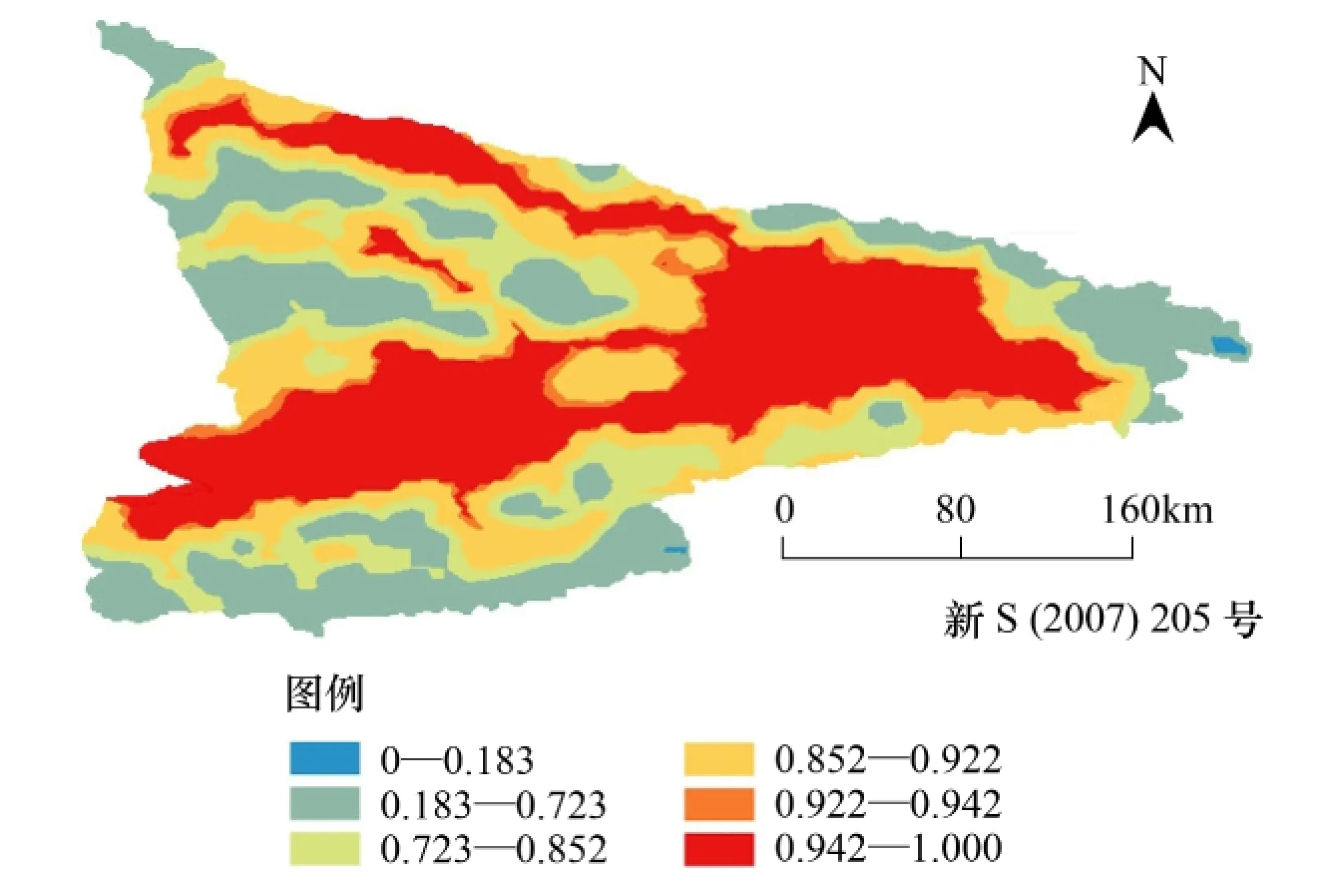
图6　2006遥感数据换算的植被覆盖指数等值线图Fig.6　The contour map of vegetation coverage index conversed by RS data of 2006

图7　2011遥感数据换算的植被覆盖指数等值线图Fig.7　The contour map of vegetation coverage index conversed by RS data of 2011

2　模型选择与拟合方法

2.1线性回归模型

一般线性回归模型的表达形式如下：

Yi=α0+α1Xi1+α2Xi2+εii=1,2,…,n

(1)

式中,Yi为第i个点的植被覆盖指数，Xi1为第i个点的年均降水量，Xi2为第i个点的年均气温；α0为平均基准植被覆盖指数，α1为降水量对植被覆盖指数的平均影响强度，α2为温度对植被覆盖指数的平均影响强度，εi为残差。

2.2空间变系数回归模型

本文选用的空间变系数回归模型为：

Yi=β0(ui,vi)+β1(ui,vi)Xi1+β2(ui,vi)Xi2+εii=1,2,…,n

(2)

式中,ui为第i个位置的横坐标，vi为第i个位置的纵坐标，Xi1、Xi2与(1)式相同。 β0(ui,vi)为第i个位置的基准植被覆盖指数，β1(ui,vi)为第i个位置降水量对植被覆盖指数的影响强度，β2(ui,vi)为第i个位置温度对植被覆盖指数的影响强度。 对于空间变系数模型，张辉国等[17]基于GWR方法和局部线性GWR方法提出了稳健性GWR方法来处理异常值，这种方法可以降低异常值对回归系数估计的影响。王宁等[18]通过数值模拟比较了GWR方法和局部线性GWR方法的相应结果，说明局部线性GWR方法在减小回归系数函数估计的边界效应和偏差方面的优良性。由于空间变系数模型的系数函数是空间地理位置坐标的二元函数，因此其二维地理区域边界部分要比一维区域边界部分大。为了使系数函数在边界区域的估计不失真，本文采用局部线性GWR方法进行拟合：

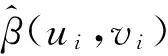
式中,dij为(ui,vi)到(uj,vj)的欧氏距离，使用交叉确认法来确定光滑参数h的值，得到光滑参数值h=15.68km。

3　结果分析

本文以2011年的数据来说明计算过程，2006年数据计算方法相同，不再赘述。

3.1对线性回归模型的估计结果进行列表分析

由表1可以看出伊犁地区的基准植被覆盖指数约为0.608，通过对α0，α1，α2进行显著性检验(显著性水平为0.05)证明了降水量和温度对植被覆盖指数的影响都是显著的。但是线性回归方法也存在弊端，因为结果表明，伊犁地区835个不同地理位置的基准植被覆盖指数均为0.608，降水量对植被覆盖指数的影响强度均为0.41‰，温度影响强度为0.014，即这些值在空间上没有变化，显然这种结果是不合理的。

3.2对空间变系数模型的估计结果进行列表分析

如表3所示，由于所有检验的P值都很小，因此说明整个回归关系具有显著的空间非平稳性，同时各系数函数随空间地理位置变化也具有高度的显著性。具体而言，伊犁地区的植被覆盖指数具有显著的变化，同时不同区域的降水量和温度对植被覆盖指数的影响以及影响强度也有显著的不同。

表1　2011年数据的线性回归模型的最小二乘估计

*** 0.001,** 0.01,* 0.05,. 0.1

表2　2011年数据的空间变系数模型的局部线性GWR估计

表3　2011年数据的空间变系数模型的三阶矩χ2逼近方法检验的P值

3.3局部线性GWR估计

3.4植被覆盖指数的模拟值及误差值的等值线图

对比图6—图15两年数据的结果分析，由线性最小二乘估计得到的模拟值与实测值之间有很大的差异，由局部线性GWR估计得到的模拟值与实测的植被覆盖情况基本一致，从而体现了局部线性GWR估计方法的准确性。图14和图15分别为2006和2011年植被覆盖指数的实测值与局部线性GWR估计的模拟值之差的等值线图，两年数据估计结果的误差基本一致，观测对比误差的空间分布可以认为主要是由降水、气温之外的地形、地貌及人类活动等多种因素造成的，需要进一步研究。其中自东向西的巩留-伊宁-霍城县的伊犁河段为正向误差，可能是由于这一河段是农业种植区或是山前倾斜平原，也是该地区人口相对密集带[16]； 山地地区一般为海拔较高的天然草地和天然牧场的分布区，该区域的负向误差可能是由于在模型中未考虑一定海拔之上温度过低，不利于植被生长，即降水量高但温度低的地区植被也应该弱，但由于其机理比较复杂，需进一步细化模型。

4　结论

(1)空间变系数回归模型拟合结果表明，就伊犁地区独特的地理单元而言：降水量和温度对植被覆盖指数的影响具有显著的空间非平稳性特征。

(2)空间变系数回归模型可以用于变量间的空间相关分析，该模型将数据的地理位置引入回归系数中，有效地反映了回归关系的空间异质性，计算结果与植被的实际分布基本吻合。

图8　2006线性最小二乘估计的植被覆盖指数的模拟图Fig.8　The simulation figure of vegetation coverage index by linear least squares estimation of 2006

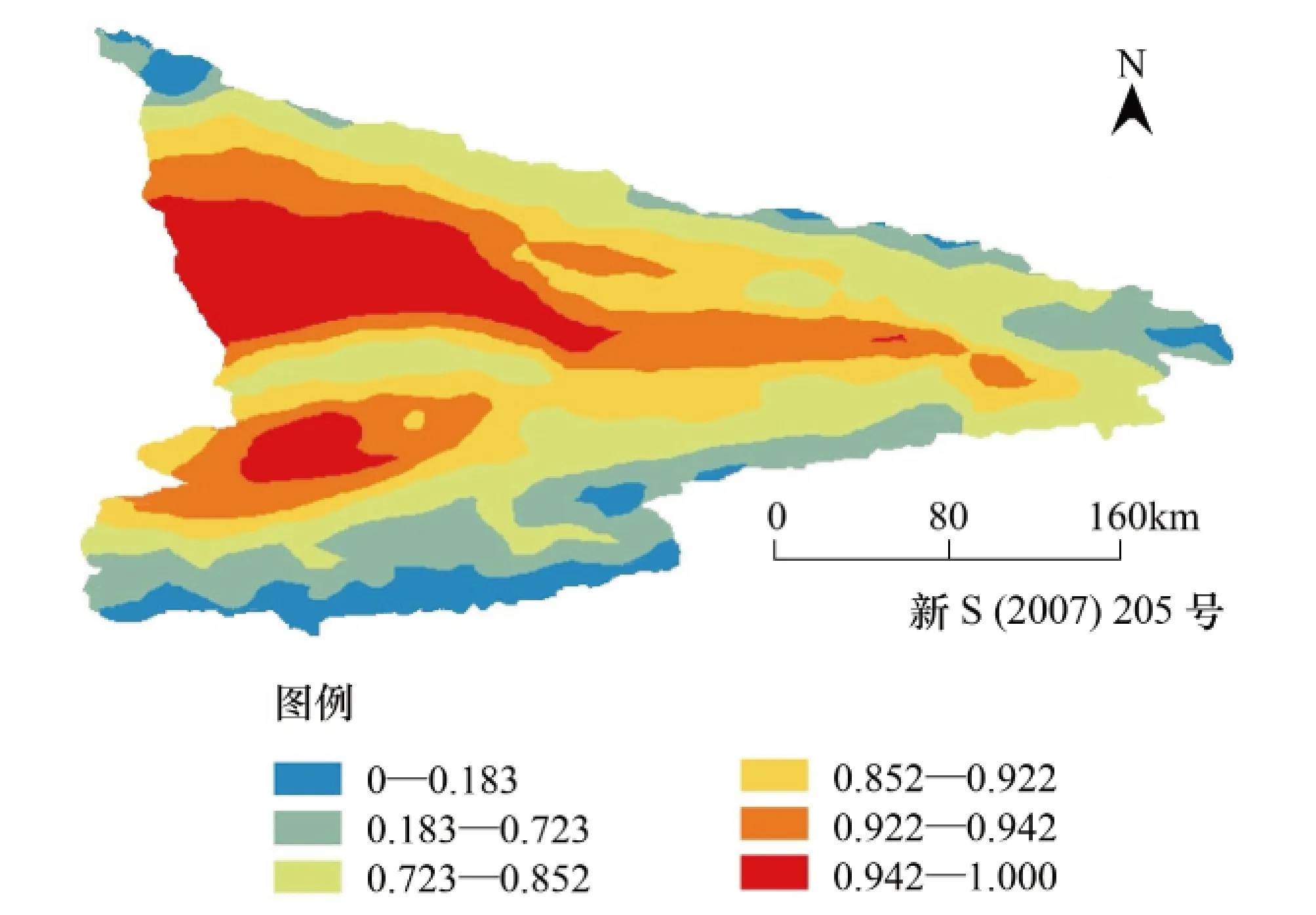
图9　2011线性最小二乘估计的植被覆盖指数的模拟图Fig.9　The simulation figure of vegetation coverage index by linear least squares estimation of 2011

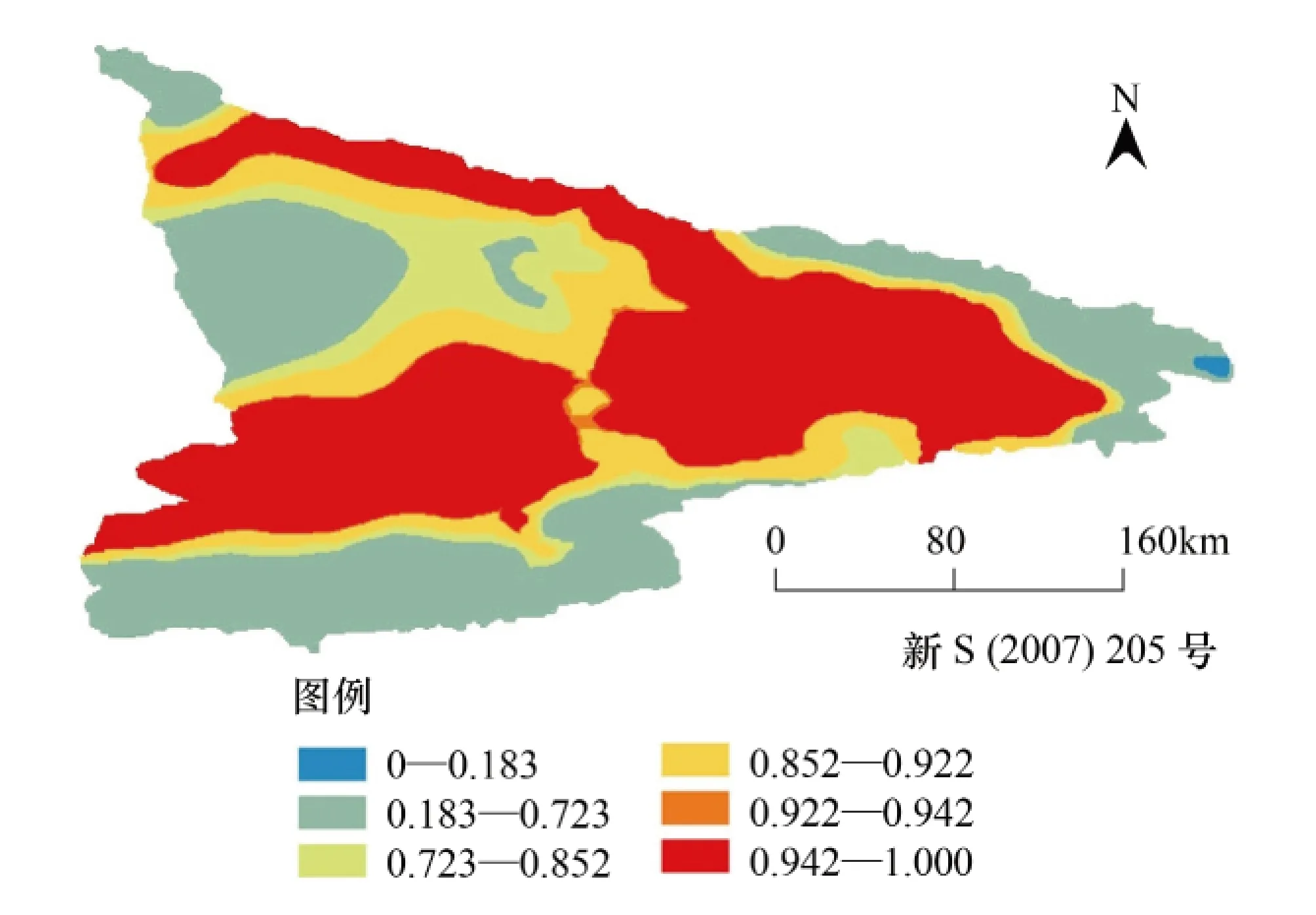
图10　2006局部线性GWR估计的植被覆盖指数的模拟图Fig.10　The simulation figure of vegetation coverage index by local linear GWR estimation of 2006

图11　2011局部线性GWR估计的植被覆盖指数的模拟图Fig.11　The simulation figure of vegetation coverage index by local linear GWR estimation of 2011

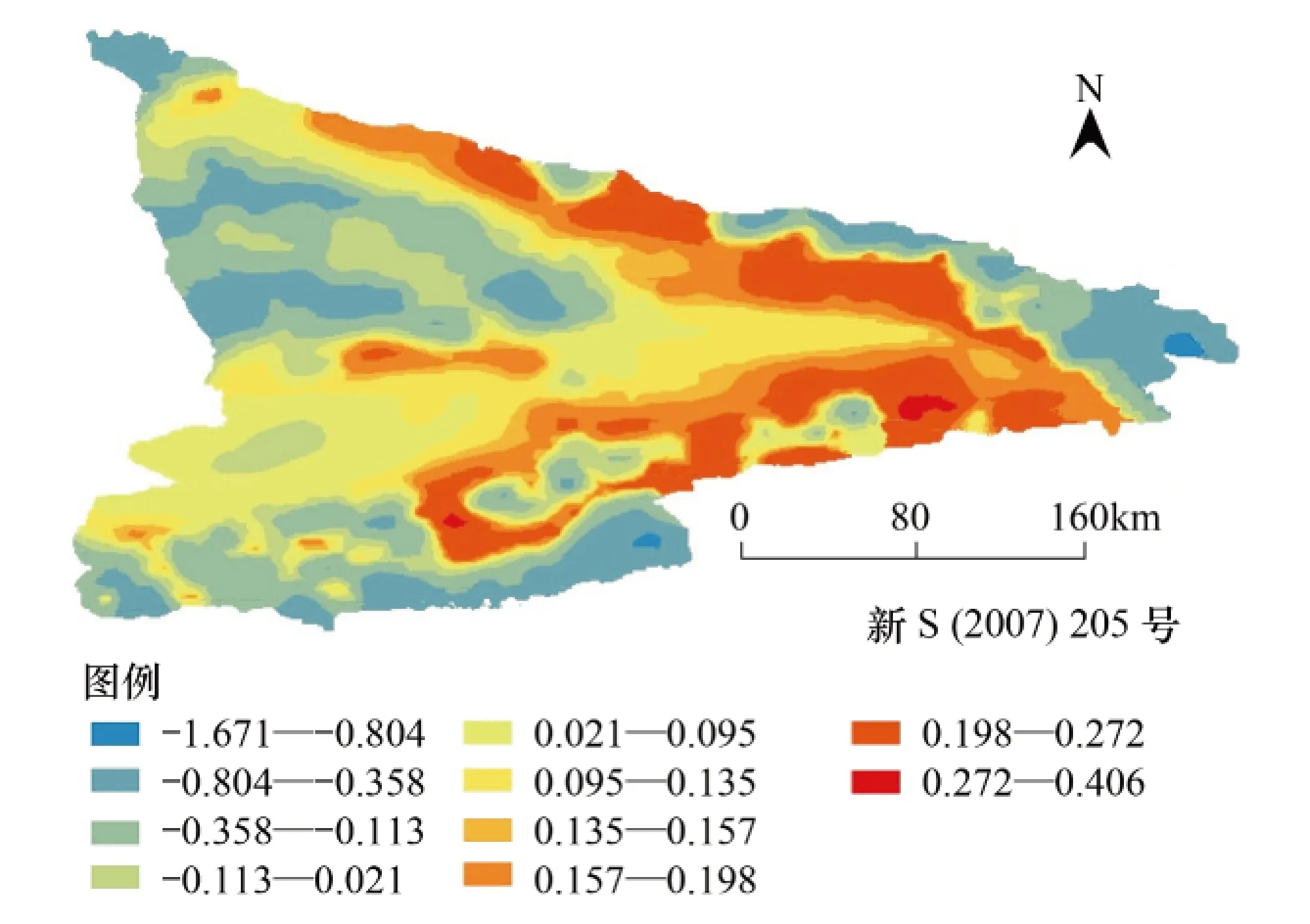
图12　2006线性最小二乘估计的植被覆盖指数的模拟误差图Fig.12　The simulation error figure of vegetation coverage index by linear least squares estimation of 2006

图13　2011线性最小二乘估计的植被覆盖指数的模拟误差图Fig.13　The simulation error figure of vegetation coverage index by linear least squares estimation of 2011

图14　2006局部线性GWR估计的植被覆盖指数的模拟误差图Fig.14　The simulation error figure of vegetation coverage index by local linear GWR estimation of 2006

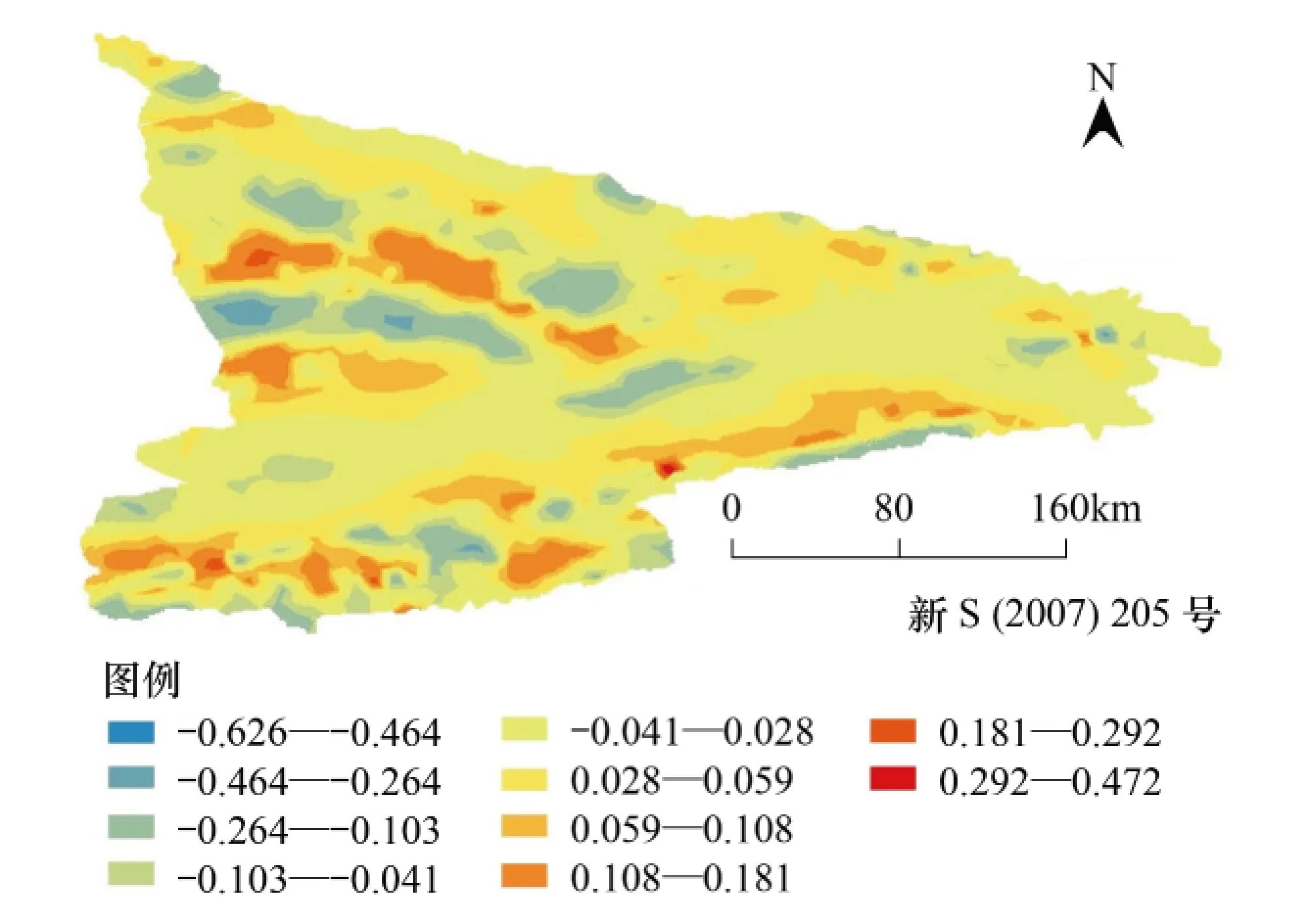
图15　2011局部线性GWR估计的植被覆盖指数的模拟误差图Fig.15　The simulation error figure of vegetation coverage index by local linear GWR estimation of 2011

(3)局部线性GWR估计方法明显优于线性回归最小二乘估计。

(4)空间变系数回归模型有效地反映了回归关系的空间非平稳性特征，这为单期数据情况下具有空间相关性变量计算提供了解决方法。

(5)模型估计误差是降水、气温之外的地形、地貌及人类活动等多种因素造成的。

[1]胡志斌, 何兴元, 李月辉, 朱教君, 李小玉. 岷江上游地区人类活动强度及其特征. 生态学杂志, 2007, 26(4): 539-543.

[2]宋怡, 马明国. 基于SPOTVEGETATION数据的中国西北植被覆盖变化分析. 中国沙漠, 2007, 27(1): 89-93.

[3]师庆东, 王智, 贺龙梅, 师庆三, 阿斯姆古丽·阿纳耶提, 刘曼, 常顺利. 基于气候、地貌、生态系统的景观分类体系——以新疆地区为例. 生态学报, 2014, 34(12):3359-3367.

[4]孙鹏森, 刘世荣, 李崇巍. 基于地形和主风向效应模拟山区降水空间分布. 生态学报, 2004, 24(9): 1910-1916.

[5]辛渝, 陈洪武, 张广兴, 张新, 卢戈, 博力健. 新疆年降水量的时空变化特征. 高原气象, 2008, 27(5): 993-1003.

[6]邱新法, 仇月萍, 曾燕. 重庆山地月平均气温空间分布模拟研究. 地球科学进展, 2009, 24(6): 621-628.

[7] 孙红雨, 王长耀, 牛铮, 布和敖斯尔, 李兵. 中国地表植被覆盖变化及其与气候因子关系——基于NOAA时间序列数据分析. 遥感学报, 1998, 2(3):204-210.

[8]李震, 阎福礼, 范湘涛. 中国西北地区NDVI变化及其与温度和降水的关系. 遥感学报, 2004, 9(3): 308-313.

[9]师庆东, 肖继东, 潘晓玲, 吕光辉, 陆海燕. 近20a来新疆植被覆盖变化特征研究. 干旱区研究, 2004, 21(4): 389-394.

[10]王智, 师庆东, 常顺利, 吴友均, 梁凤超. 新疆地区平均气温空间插值方法研究. 高原气象, 2012, 31(1):201-208.

[11]王智, 吴友均, 梁凤超, 师庆东,常顺利. 新疆地区年降水量的空间插值方法研究. 中国农业气象,2011,32(3):331-337.

[12]刘芳, 张红旗, 董光龙. 伊犁河谷草地植被NDVI变化及其降水敏感性特征. 资源科学, 2014, 36(8):1724-1731.

[13] 李晓松, 高志海, 李增元, 白黎娜, 王琫瑜. 基于高光谱混合像元分解的干旱地区稀疏植被覆盖度估测. 应用生态学报, 2010, 21(1): 152-158.

[14] Guman G, Ignatov A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. International Journal of Remote Sensing, 1988, 19(8):1533-1543.

[15] Zeng X B, Dickinson R E, Walker A, Shaikh M, DeFries R S, Qi J G. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. Journal of Applied Meteorology, 2000 39(6):826-839.

[16]王倩, 杨太保, 杨雪梅. 新疆伊犁河流域植被变化动态监测与评价. 干旱区资源与环境, 2015, 29(8):126-131.

[17]Zhang H G, Mei C L. Local least absolute deviation estimation of spatially varying coefficient models: Robust geographically weighted regression approaches. International Journal of Geographical Information Science, 2011, 25(9):1467-1489.

[18]Wang N, Mei C L, Yan X D. Local linear estimation of spatially varying coefficient models: An improvement on the geographically weighted regression technique. Environment and Planning A, 2008, 40(4):986-1005.

[19]Brunsdon C, Fotheringham A S, Charlton M E. Geographically weighted regression: A method for exploring spatial non-stationarity. Geographically Analysis, 1996, 28(4):281-298.

[20]王智, 师庆三, 王涛, 师庆东, 常顺利, 张履冰. 1982-2006年新疆山地—绿洲—荒漠系统植被覆盖变化时空特征. 自然资源学报, 2011, 26(4):609-618.

[21]陈冬花, 邹陈, 王苏颖, 李虎, 张新时. 基于DEM的伊犁河谷气温空间插值研究. 光谱学与光谱分析, 2011, 31(7):1925-1929.

[22]赵丽, 杨青, 韩雪云. 1961-2009年伊犁地区降水指数的时空分布及变化特征分析. 干旱区资源与环境, 2014, 28(10):82-89.

[23]叶佰生, 赖祖铭, 施雅风. 伊犁河流域降水和气温的若干特征. 干旱区地理, 1997, 20(1):46-52.

[24]张军民. 伊犁河流域气候资源特点及其时空分布规律研究. 干旱气象,2006, 24(2):1-4.

[25]易浪, 任志远, 张翀, 刘雯. 黄土高原植被覆盖变化与气候和人类活动的关系. 资源科学, 2014, 36(1):0166-0174.

[26]杜灵通, 田庆久. 宁夏植被覆盖动态变化及与气候因子的关系. 中国沙漠, 2012, 32(5):1479-1485.

[27]穆少杰, 李建龙, 陈奕兆, 刚成诚, 周伟, 居为民. 2001—2010年内蒙古植被覆盖度时空变化特征. 地理学报, 2012, 67(9):1255-1268.

[28]韦振锋, 王德光, 张翀, 刘宪锋, 张晗. 1999—2010年中国西北地区植被覆盖对气候变化和人类活动的响应. 中国沙漠, 2014, 34(6):1665-1670.

[29]杨光华, 包安明, 陈曦, 刘海隆, 黄莹, 代述勇. 1998—2007年新疆植被覆盖变化及驱动因素分析. 冰川冻土, 2009, 31(3):436-445.

[30]李秀花, 师庆东, 郭娟, 常顺利, 齐家国. 中国西北干旱区1981—2001年NDVI对气候变化的响应分析. 中国沙漠, 2009, 29(5):989-994.

Spatial non-stationarity characteristics of the impacts of precipitation and temperature on vegetation coverage index: a case study in Yili River Valley, Xinjiang

FENG Jinjie1, ZHANG Huiguo1, HU Xijian1*, SHI Qingdong2, ZUbaidai·Muyibula2

1CollegeofMathematicsandSystemSciences,XinjiangUniversity,Urumuqi830046,China2InstituteofAridLandEcologyandEnvironmentatXinjiangUniversity,Urumuqi830046,China3MinistryofEducationKeyLaboratoryofOasisEcology,Urumuqi830046,China

The multivariable spatial correlation analysis is mainly based on time series data and requires long-term time series for statistical analysis. The analysis of spatial non-stationary characteristics can determine the relationship between multivariate variables by using single a single dataset. Based on the spatially varying coefficient regression model, this study analyzed the spatial variation characteristics of the vegetation coverage index in response to precipitation and temperature in the Yili area of Xinjiang in 2006 and 2011. The regression coefficient map estimated by using the local linear geographical weighted regression(GWR) method further revealed that the spatial heterogeneity of the interaction between the variables. The results were compared against linear least squares regression method. The main findings are the following: (1)The spatially varying coefficient regression model can be used to analyze the spatial correlation between variables. (2) The local linear GWR is superior to the linear least squares regression method. (3) Results showed a clearly spatial non-stationary characteristics of the vegetation coverage index under the effects of precipitation and temperature in the Yili area of Xinjiang. (4) In addition to precipitation and temperature, factors such as topography, geomorphology and human activities can cause deviations in the estimation, which requires further research. This paper provides new ideas and methods to analyze spatial correlation between variables that exhibit spatial non-stationary characteristics and to obtain spatial simulation distribution of the vegetation coverage index.

Yili area; spatially varying coefficient regression model; local linear Geographically Weighted Regression (GWR); vegetation coverage index; precipitation; temperature

国家自然科学基金资助项目(31160114, 41261087)；新疆大学博士启动基金项目(BS130103)；新疆自然科学基金资助项目(2015211C276)

2015- 06- 10;

2015- 12- 29

Corresponding author.E-mail: xijianhu@126.com

10.5846/stxb201506101166

冯金杰，张辉国，胡锡健，师庆东，祖拜代·木依布拉.降水量和温度对植被覆盖指数影响的空间非平稳性特征——以新疆伊犁河谷地区为例.生态学报,2016,36(15):4626- 4634.

Feng J J, Zhang H G, Hu X J, Shi Q D, Zubaidai.Muyibula.Spatial non-stationarity characteristics of the impacts of precipitation and temperature on vegetation coverage index: a case study in Yili River Valley, Xinjiang.Acta Ecologica Sinica,2016,36(15):4626- 4634.