“万有引力”疑难问题辨析

陈　坤　印晓明

(江苏省南菁高级中学,江苏　无锡　214437)



“万有引力”疑难问题辨析

陈坤印晓明

(江苏省南菁高级中学,江苏无锡214437)

在学习高中物理“万有引力与航天”部分时，学生常常提出一些问题，如宇宙速度的求法、开普勒第三定律中比值的含义以及两质点在万有引力作用下作变加速运动的特殊处理方法等，本文针对这些问题提出解决方案，可有效拓展学生的视野.

万有引力定律；宇宙速度；开普勒第三定律

在高中物理教科书“万有引力”一节中，编者考虑到高中学生的实际水平，往往直接给出结论，如开普勒第三定律、第二和第三宇宙速度等，教师授课时也一带而过，课后学生却感觉不过瘾，一些善于钻研的学生，往往要围着老师，追根穷源.因此，在课外培优时，笔者通过补充部分知识，解决学生常提的一些疑难问题，大大激发了学生兴趣，取得了较好的教学效果.

1　第二和第三宇宙速度

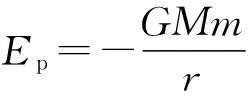
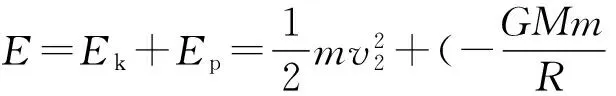
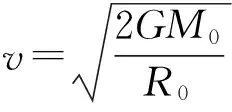
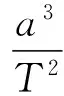
对于行星做椭圆运动，如图1所示，设太阳M在椭圆的一个焦点F上，行星m围绕太阳做椭圆运动，椭圆的半长轴和半短轴分别为a和b，

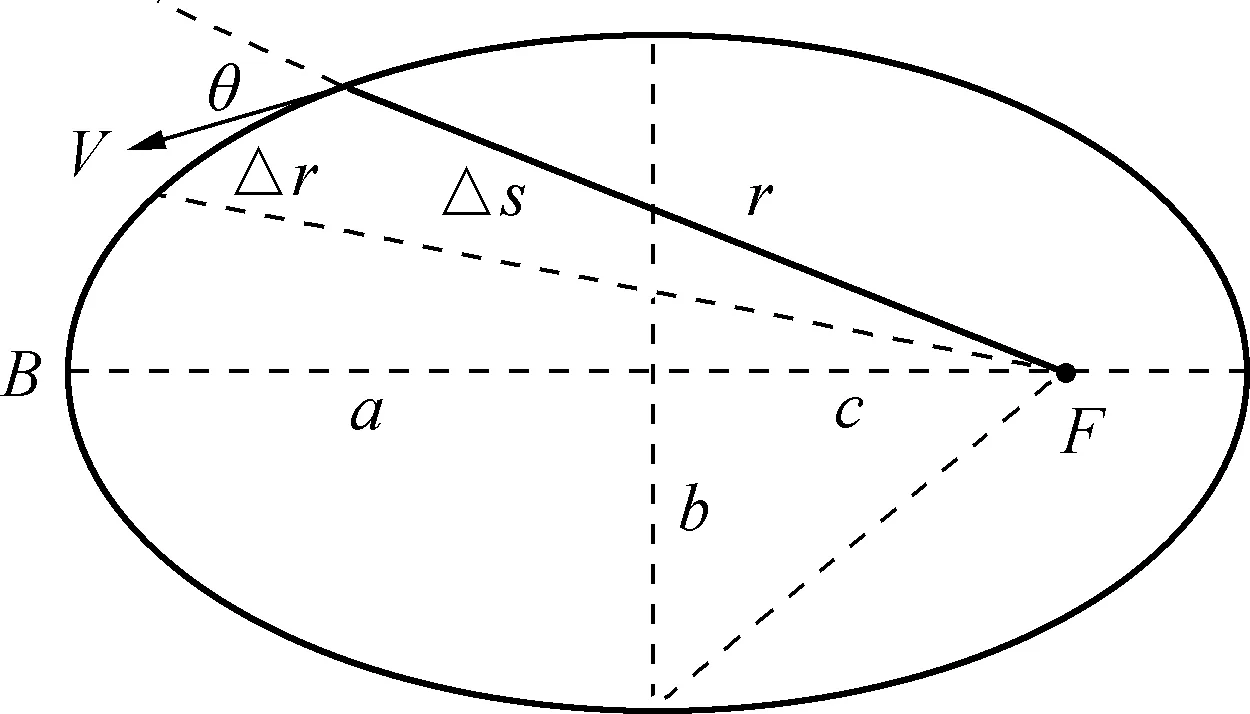
图1

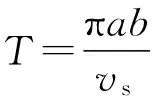
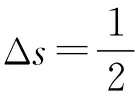
3　计算两个物体相遇的时间

在近地附近物体做自由落体运动时，可认为物体做加速度恒为g的匀加速运动，物体在距离地面较远处下落时落地时间如何计算？物体在中心天体引力作用下做直线运动时，加速度不断变化，不能视为自由落体.此时可以采用极限思想，将该直线运动视为一个“退化”的椭圆运动，该椭圆的短轴b=0，则a=c，于是到达中心天体的时间为椭圆运动周期的一半.

例1：宇宙空间有质量分别为m1和m2的两个质点相距L，m2固定，从静止开始，m1在万有引力的作用下运动，试求从开始运动到二者相遇所需的时间.

在双星系统中，一质量较大的天体向一中心天体运动时，严格意义上来讲，中心天体也会向其靠近，中心天体将不再固定，该如何解决？解决该问题的关键在于求出等效的中心天体的质量.

例2：作为上题的引申，宇宙空间有质量分别为m1和m2的两个质点，相距L，从静止开始，在万有引力的作用下相向运动，试求从开始运动到相遇所需的时间.

解析：m2加速向m1运动，若m1静止，问题很简单，难点在于m1也在向m2加速运动，m1所在的参考系为非惯性系，因此，分析m2的受力时除考虑二者的万有引力之外，还应考虑“施加”在m2上的“惯性力”.该“惯性力”的大小为m2a1，方向是从m2指向m1.

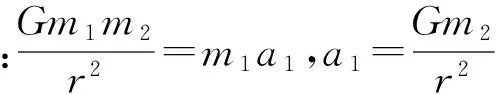
图2

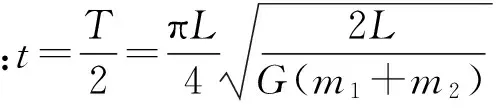
由上述问题可以发现，教师钻研的部分动力来自学生的追问，学生无尽的追问促使教师不断发展，这就是“教学相长”在物理课堂上的最好体现.

[1] 周复忠.万有引力教学中的一、二、三[J].物理之友，2016,32(4).

[2] 朱柏树.行星在椭圆轨道近(远)地点的向心力等于万有引力吗——由课堂争论引发的教学研讨[J].物理之友，2015,31(5).

[3] 黄俊杰.紧扣“三个半径”突破“天体运动”的难点[J].物理之友，2015,31(7).