RL电路特性的定量研究

王　慧　李国文　仲扣庄

(1. 南京师范大学教师教育学院，江苏　南京　210097；2. 南京师范大学物理科学与技术学院，江苏　南京　210023)



RL电路特性的定量研究

王慧1李国文1仲扣庄2

(1. 南京师范大学教师教育学院，江苏南京210097；2. 南京师范大学物理科学与技术学院，江苏南京210023)

笔者定量研究RL电路中电压、电流之间相位差的变化规律，探究电感、电阻和信号频率对电压、电流之间相位差的影响.

RL电路；相位差；控制变量法

1　实验原理

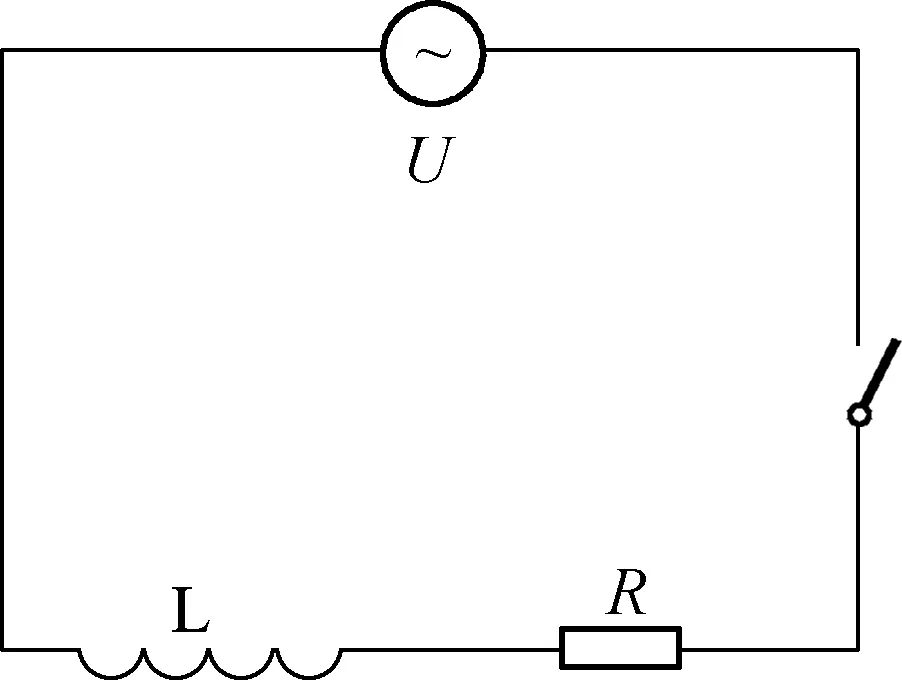
图1

根据上述讨论，保持L和R大小不变时，随着ω的增大，电源电压与电流之间的相位差Δφ逐渐增大；保持ω和L不变时，随着R的增大，相位差Δφ逐渐减小；保持ω和R不变时，随着L的增大，相位差Δφ逐渐增大.

2　实验方案

笔者采用控制变量法，测量当f、R、L中单个变量改变时的相位差，分析相位差的变化规律.

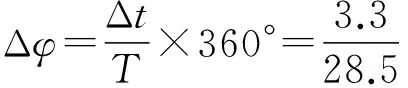
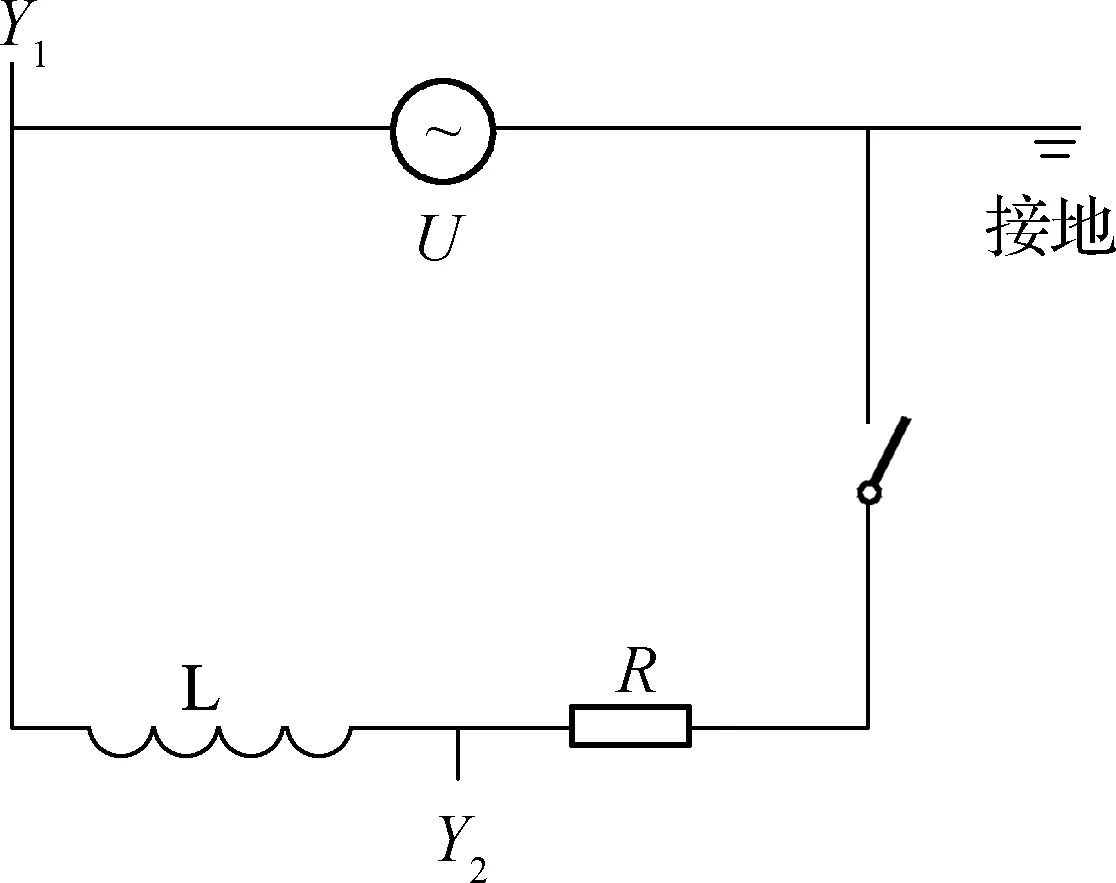
图2

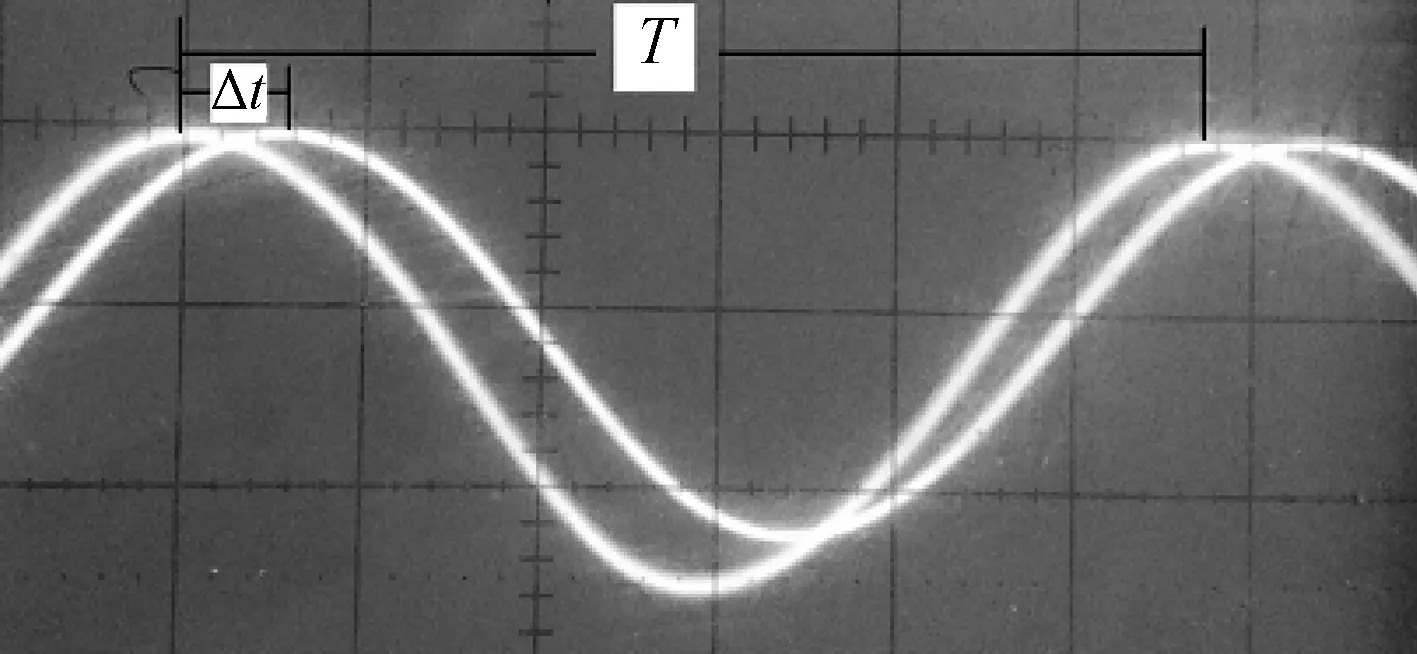
图3

3　实验数据处理和分析

3.1验证相位差Δφ与电阻R的关系

保持正弦信号源频率为1kHz，改变电阻R，分别观察接入电感为0.01H和0.1H时，电源电压与电流的之间的相位差Δφ与接入电阻R之间的关系，数据记录见表1和表2，相位差Δφ与电阻R关系曲线图像如图4、图5.

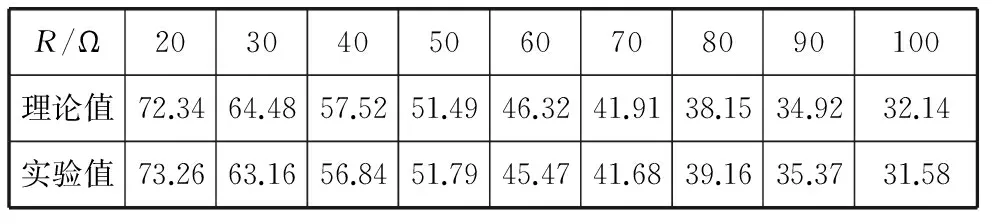
表1　相位差Δφ与电阻R的关系　(f=1kHz，L=0.01H)

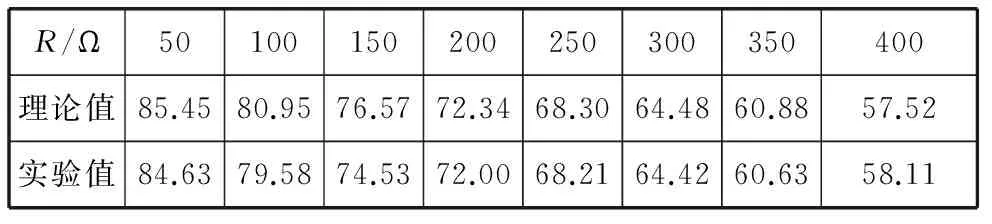
表2　相位差Δφ与电阻R的关系　(f=1kHz，L=0.1H)

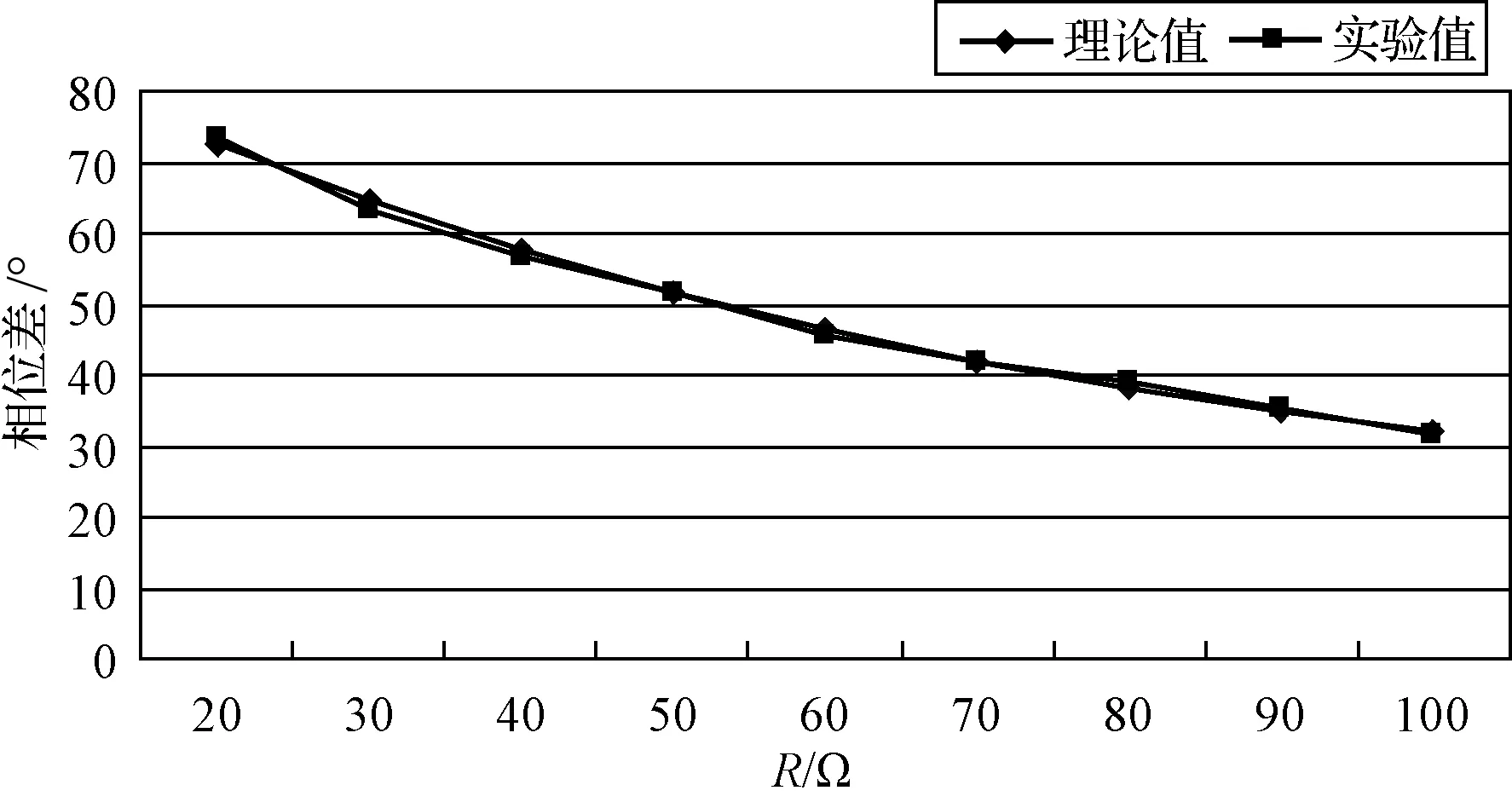
图4　L=0.01H时的Δφ-R图像

图5　L=0.1H时的Δφ-R图像

误差分析：当L=0.01H时，百分误差E=0.33%；当L=0.1时，百分误差E=0.67%.表1和表2中低频信号的频率都是1kHz,电感L分别是0.01H和0.1H，从图4和图5中我们可以看出：RL电路中随着电阻的增大，电压与电流之间的相位差Δφ逐渐减小.

3.2探究相位差Δφ与信号源频率f的关系

保持接入电阻R=40Ω，分别观察接入电感为0.01H和0.1H时，电压与电流之间的相位差Δφ与电源频率f之间的关系，数据记录见表3和表4，相位差Δφ与信号源频率f关系图像如图6、图7.

表3　相位差Δφ与信号源频率f的关系　(R=40Ω，L=0.01H)

表4　相位差Δφ与信号频率f的关系　(R=40Ω，L=0.1H)

图6　L=0.01H时的Δφ-f图像

图7　L=0.1H时的Δφ-f图像

误差分析：当L=0.01H时，百分误差E=1.67%；当L=0.1H时，百分误差E=0.23%.图6和图7表明：随着信号源频率f的增大，电压电流之间的相位差逐渐增大.

3.3探究相位差Δφ与电感L的关系

保持接入电阻R=40Ω，记录不同信号源频率下，电感L=0.01H与L=0.1H所对应的相位差的大小.实验数据记录见表5，相位差Δφ与电源频率f关系曲线如图8.

表5L=0.01H、L=0.1H时的相位差Δφ对比(R=40Ω)

f/kHz1.01.52.02.5L=0.01/H56.8466.9674.2079.78L=0.1/H84.6387.1688.4289.68

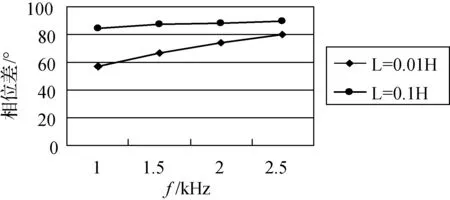
图8　Δφ-f图像

从图8中可以看出:当接入RL电路的电阻、信号源频率f相同时，接入的电感L越大，电压与电流之间的相位差Δφ也越大，电感对电流的阻碍作用越强.

4　实验总结

(1) 选择合适的电阻，电阻过小，波形图趋于平缓，难以记录数据；电阻过大，波形太密，读取的数据误差较大.

(2) 选取的电感越大，相位差的变化率越缓慢，测量时应扩大电阻的范围.若电阻在小范围内变化，相位差的改变较小，实验的误差也会增大.

(3) 注意线路是否连接良好，当波形图呈现一条直线时，有可能是线路接触不良.

[1] 李瀚荪.电路分析基础(上册)[M].北京：高等教育出版社，2006.

[2] 江燕，夏雪琴.RC、RL及RCL串联电路幅频和相频特性的研究[J].大学物理实验，2012，25(5).

[3] 刘竹琴.基于RCL串联谐振实现电感的测量[J].信息技术，2014，(8).

名师简介：仲扣庄(1962—)，男，江苏盐城人，博士，南京师范大学物理科学与技术学院教授、硕士生导师，主要研究物理课程与教学论.