基于马尔科夫过程的珠江流域干旱特征研究

肖名忠， 张强， 孔冬冬， 张正浩

(1.中山大学 水资源与环境系，广东 广州 510275;2.中山大学 华南地区水循环与水安全广东省普通高校重点实验室，广东 广州 510275)



基于马尔科夫过程的珠江流域干旱特征研究

肖名忠1，2， 张强1，2， 孔冬冬1，2， 张正浩1，2

(1.中山大学 水资源与环境系，广东 广州 510275;2.中山大学 华南地区水循环与水安全广东省普通高校重点实验室，广东 广州 510275)

对干旱转移概率的有效把握是干旱预报的关键，进而能够用于减轻干旱危害。基于此，根据Copula函数导出了马尔科夫链的转移概率矩阵。将干旱分为了6种状态，干旱事件和干旱状态不同，当干旱事件的严重程度不小于某一干旱状态时，在本文中就被定义为具有该严重程度的干旱事件。为了研究珠江流域的干旱特征，对某一严重程度干旱事件的平均历时、从任一干旱状态到没有干旱状态的平均首达时间、以及从没有干旱状态到某一严重干旱事件的平均首达时间进行了分析。研究结果表明：①非常极端干旱事件持续约1.5个月，轻微干旱事件持续约3个月；②从非常极端干旱状态恢复到没有干旱状态需要约3.5个月，从轻微干旱状态恢复到无旱情需要约1.7个月的时间；③一般来说，珠江流域平均0.5 a中有一次中等干旱事件，1 a中有一次严重干旱事件，1.5 a中有一次极端干旱事件，以及3.5 a中有一次非常极端干旱事件。此外，研究结果还表明,珠江流域东南部地区干旱风险较高，而该地区人口稠密、经济发达，特别是其中的珠三角地区，因而需要特别重视干旱风险。同时，珠江流域西部地区也是干旱风险较高的区域。

干旱；马尔科夫链； Copula函数；转移概率；标准化降水蒸散发指数(SPEI)

干旱通常定义为在某一段时间内的持续缺水现象，由于持续时间长，干旱会导致水循环过程中的严重水量失衡，会对农业、城市供水、公共卫生、生态系统、能源以及经济等造成严重影响[1]。具体来说，干旱会对农业、城市、供水、公共卫生、生态系统、能源以及经济等造成严重影响[2-3]。据估计，美国由于干旱造成的经济损失每年高达80亿美元，远超其他气象灾害造成的损失[4]。同时,近年来随着人口的快速增多，农业、能源、经济的快速发展，对水资源的需求量正成倍增加，从而导致世界上很多地区几乎每年都有缺水事件发生[1]，尤其是气候变化和水污染等因素更进一步加剧了缺水状况[5]。因而，干旱的成因、影响和变化规律以及风险的评估正得到各国学者的广泛重视[6-11]。

实际上，目前监测干旱状况以及评估缺水状态的指数很多，各指数详细的优缺点可以参考Mishra和Singh写的综述[1]。标准化降水指数(Standardized Precipitation Index，SPI)由于计算简单，同时能够用不同时间尺度描述短期和长期的干旱，被广泛运用于干旱的各个属性的监测[6-8, 11-13]。然而随着全球变暖，蒸散发也增加，这将极大影响干旱的严重程度，因而作为SPI的一个扩展，Vicente-Serrano等[14]提出了标准降水蒸散发指数(Standardized Precipitation Evapotranspiration Index，SPEI)。SPEI被设计成同时考虑降水和潜在蒸散发的影响监测干旱，更能捕捉气温升高对干旱的影响，其在干旱的分析和评估领域也得到了广泛的运用[14-16]，本文将SPEI作为干旱监测的指标。

相比于洪水、地震、飓风等极端自然灾害，干旱发生过程非常缓慢，因而在预报到位的情况下可以对干旱灾害进行预防，从而减轻干旱的影响。同时用SPEI描述的干旱过程可近似看作为一个随机过程，可以用随机方法描述。Sanusi等[13]基于一阶的均质马尔科夫过程，用1个月时间尺度的SPI对马来西亚半岛的干旱特征，如平均复发时间以及干旱的平均首达时间等进行了分析。Paulo和Pereira[17]基于均质和非均质的马尔科夫过程，对干旱状态的转移概率特征进行了分析。这些研究结果发现，随机模型能够很好地用于干旱演变过程的监测，从而为干旱的预防提供有用信息。

传统的基于最大似然法估计的马尔科夫转移概率矩阵的有效性受到了Cancelliere等[12]的质疑。有研究发现,由于样本数过少，在某些情况下会导致计算出的转移概率为零，这是非常不合理的。为避免传统最大似然估计方法的缺陷，Cancelliere等[12]根据SPI的性质推导出了计算转移概率矩阵的理论方法。但这个方法也是有争议的，Madadgar等[18]认为该方法所基于的相互独立以及正态分布的假设并不是经常成立的，同时指出,根据SPI计算转移概率矩阵的繁琐复杂过程可以通过建立用Copula函数表示的多变量相关性模型避免。本文介绍了一种通过Copula函数计算转移概率矩阵的理论方法。

珠江流域地处湿润气候区，雨量充沛，但近年来也遭遇到了严重的干旱事件，例如2010年的西南5省市大旱以及2011年的南方干旱[6]。这些干旱对珠江流域的社会经济发展以及生态环境造成了严重的破坏。更重要的是，珠江流域的一些支流担负着为珠江三角洲特大城市群以及香港供水的重任。据估计，在珠江三角洲城市群生活着4 000万左右的居民[19]，香港每年用水量的80%是由东江提供的[20]。因此，基于马尔科夫链对珠江流域干旱的时空演变特征进行分析将具有重要意义，可为决策者提供有用的信息，从而能更好地安排生产、生活活动，减轻干

旱灾害目前这方面的研究在珠江流域还没有做。

本文的目的是利用由Copula函数计算出的马尔科夫链转移概率矩阵研究珠江流域干旱特征。研究中将干旱分为6种状态，干旱事件和干旱状态不同，当干旱事件的严重程度不小于某一干旱状态时，在本文中就被定义为具有该严重程度的干旱事件。对于干旱事件，了解某一严重程度干旱事件持续的时间、恢复到无旱情状态的时间以及某一严重程度干旱事件的发生频率将对旱灾预防及应急管理有重大参考价值。因而，本文研究的珠江流域干旱特征是：①某一严重程度干旱事件的平均历时；②从任一干旱状态到没有干旱状态的平均首达时间；③从没有干旱状态到某一严重干旱事件的平均首达时间。3个干旱特征的示意图如图1所示。

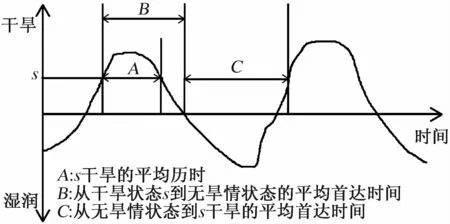
图1　 本文分析的珠江流域干旱特征示意图

1　研究区域和数据

珠江流域 (102°14′E—115°53′E；21°31′N—26°49′N) 位于中国南部，是中国河流流量第二大、流域面积第三大的流域。珠江流域面积4.573×105km2，主要由西江、北江和东江三大支流构成.由于地处热带和亚热带季风气候区，珠江流域多年平均气温在14°C到22°C，多年平均降水量1 525.1 mm，同时年内降水分布不均，全年大约80%的降水量集中在4—9月[11]。本文的研究数据来自于珠江流域内46个国家基本气象站点从1959—2013年的日降水、最高及最低气温数据，站点的位置如图2所示。

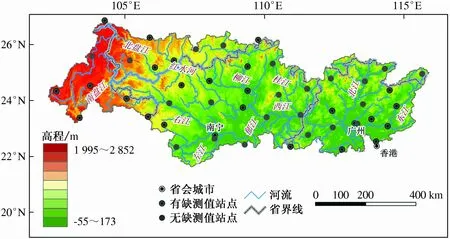
图2　 气象站点在珠江流域中的位置

图2中10个站点日降水数据有缺测值，缺测率在0.1%以下；17个站点日最高和最低气温数据有缺测值，缺测率也在0.1%以下；同时对于这些有缺测数据的站点，在图2中也进行了标注。对于这些缺测的某一天的数据，本文采用其他无缺测年份相同时间内观测值的平均值来插补，当实际值和均值相差过大时，这种方法可能会导致某些有用信息的缺失，但整体影响较小。

2　研究方法

2.1标准化降水蒸散发指数(SPEI)

为了加深气温变化对用水需求影响的了解，Vicente-Serrano等[14]提出了用SPEI指标研究干旱。SPEI被设计成同时考虑降水(P)和潜在蒸散发(PET)的影响监测干旱过程，其中潜在蒸散发指的是在水足够多的情况下所能产生的蒸发和蒸腾总量。在SPEI计算过程中，一个改进版的Hargreaves公式[21-23]被用来计算月潜在蒸散发。作为一个水分盈亏状态的简单描述，月降水和潜在蒸散发的差值可以计算为Di=Pi-PETi。同时Di值在不同时间尺度下的累积值可以表示为：

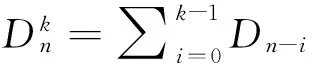
(1)

式中：k为时间尺度；n为时间。

和SPI值的计算类似[11, 24]，SPEI的计算也是通过一个等概率转换的方法将Dk序列转换成一个标准正态变量。首先用不同的分布函数拟合Dk序列，选出最优的，进而计算非超过概率F(x)，接着再将F(x)通过标准正态分布函数的反函数标准化，从而得到SPEI序列值[14]。对于一年内不同月份的Dk序列值，分别用广义正态分布(GNO)、广义帕累托分布(GP)、皮尔逊三型分布(P-III)、广义极值分布(GEV)和广义Logistic分布(GLO)拟合，其中分布函数的参数估计采用线性矩估计[25]。根据Madadgar和Moradkhani[26]的建议，最优分布函数是通过Kolmogorov-Smirnov(K-S)检验和Akaike Information Criterion(AIC)准则选取的。当分布函数通过K-S检验时，AIC值最小的将选为最优分布函数。同时，和SPI的干旱分类一样[18, 26]，SPEI的干旱分类也采用美国干旱监测中心提供的干旱分类方法，见表1。

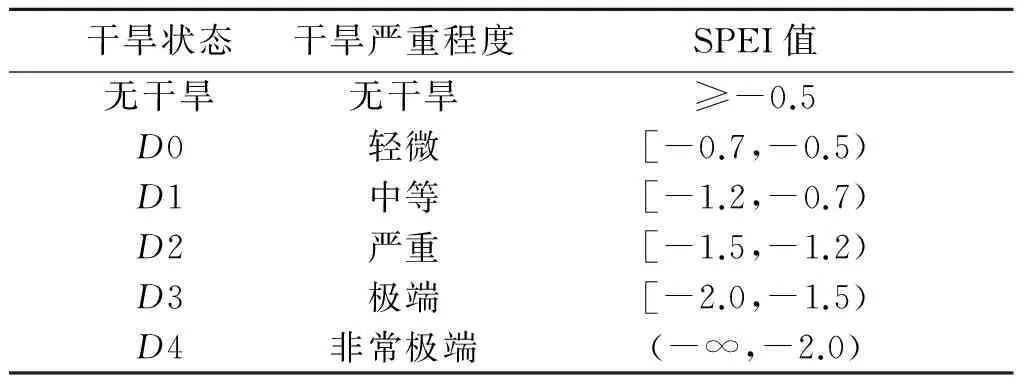
表1　 基于SPEI的干旱分类[27]

2.2Copula函数

由于构造联合分布时可以不用考虑变量的边缘分布，Copula函数已被广泛用于多变量的相关性分析中[6, 9, 18, 26, 28]。在本文中，分别选取了来自于Archimedean(Gumbel、Clayton和Frank)、Elliptical (Gaussian和 t) 和Plackett Copula家族中的6种Copula函数来描述多变量间的相关关系[27]。对于Copula函数的拟合优度检验，本文采用Cramér-von Mises 检验值(Sn)选择最优Copula函数。Cramér-von Mises 检验值定义为一个测量经验Copula函数值和参数Copula函数值(CEMP和C)差距的方法[29]，如下：

(2)

式中n为样本量。同时该拟合优度检验方法的p值是通过自举采样技术(Bootstrap Sampling)得到的[26, 29-30]，在本文中随机采样了1 000次。同样根据Madadgar和Moradkhani[26]的建议，当有好几个Copula函数在95%的置信区间内显著时，Sn值最小的Copula函数选为最优Copula函数。

2.3离散型马尔科夫链

离散型马尔科夫链，X1、X2、…、Xn、…是一个具有马尔科夫性质的随机过程，其中马尔科夫性是指后一个状态发生的概率只与前一个状态有关，也就是如下定义：

(3)

假设Pr(X1=sj|X0=si)=pij,表示的是从状态si转移到状态sj的一阶转移概率，则所有状态之间的转移概率可以用一个转移概率矩阵P表示如下：

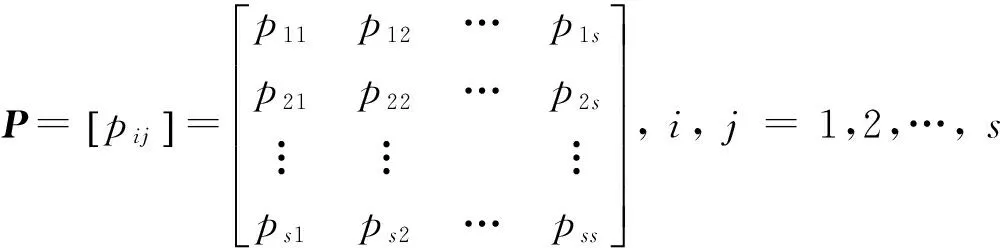
(4)

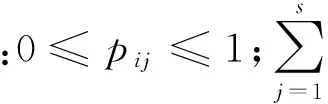
2.4Copula函数推导的转移概率

假设X和Y分别表示的是在时刻n和n-1时的干旱事件，并分别来自于u=FX(x)和v=FY(y)的分布函数。同时干旱被分为s类，类别用Ci表示，则当Y属于Ci类时，X属于Cj类的条件概率可以表示如下[12]：

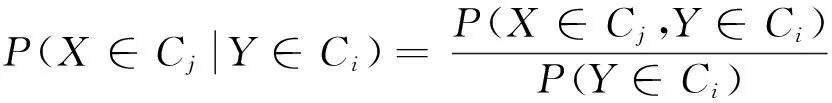
(5a)

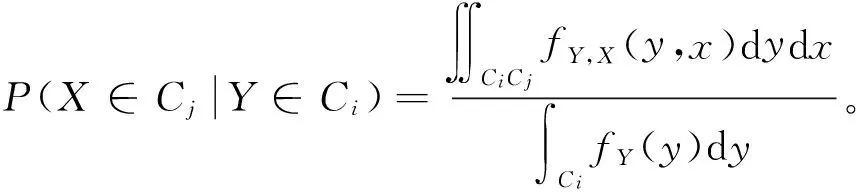
(5b)

另外，假设Ci和Cj类的上、下边界分别由si1、si2、sj1、和sj2表示，且u1=FX(sj1)、u2=FX(sj2)、v1=FY(si1)、v2=FY(si2)。则当X和Y的联合分布用Copula函数表示的情况下，公式(5b)可以进一步表示为：

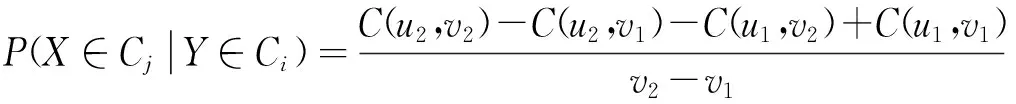
(6)

需要注意的是，式(6)中的分子可以看成是对由Ci和Cj边界构成的方形面积的计算，同时根据Copula函数推导转移概率的示意图如图3所示。

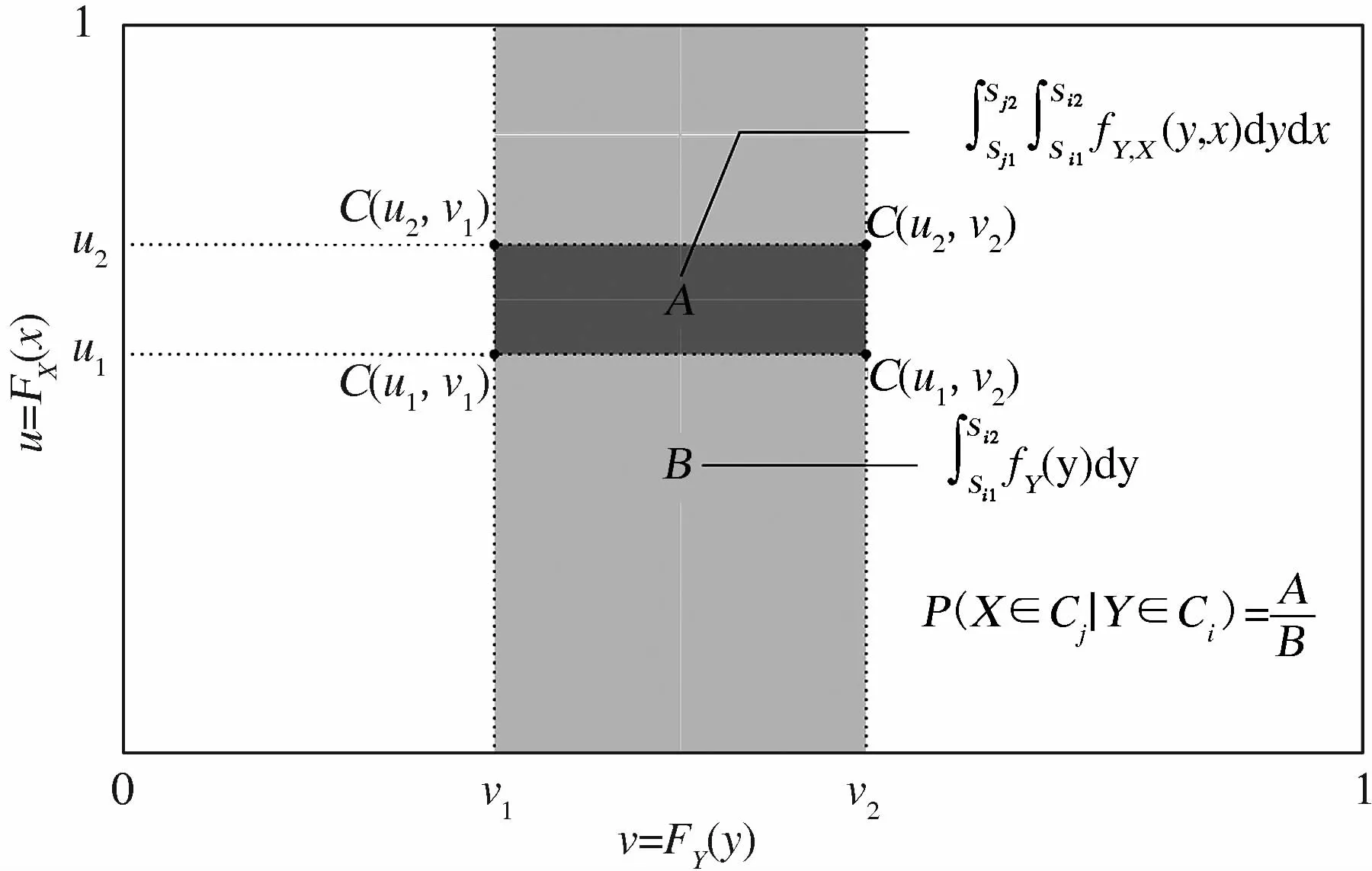
图3　基于Copula函数推导转移概率的示意图

2.5平均首达时间

设Tij表示状态si首次到达状态sj的时间，这个时间也被称为状态si到状态sj的首达时间。对于Tij，它发生的概率可以定义为：

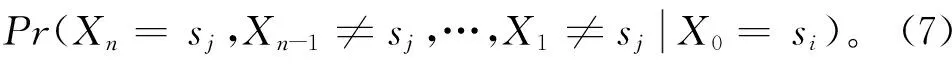
从状态si到状态sj的平均首达时间Mij，也就是期望，可以计算如下：

Mij=E[Tij=n]。

(8)

此外，对于干旱分析，某一程度干旱事件发生的频率对于干旱风险评估具有重要的意义，则很有必要计算从状态si(例如无干旱状态)到干旱事件sj+(sj+

表示的是干旱严重程度不低于sj的干旱事件)的平均首达时间。和式(7)类似，状态si到干旱事件sj+的首达时间可以表示为Tij+，从而Tij+的发生概率可以计算如下：

式中si的严重程度小于sj。

同样，Tij+的均值(用Mij+表示)也可以类似于式(8)进行计算。在本文中由于采用的马尔科夫链是非均质的，Mij和Mij+不太可能通过一个解析式来进行计算，因而本文采用随机模拟20 000次的方法计算。

2.6干旱平均历时

了解某一严重程度干旱事件持续的时间将会为干旱风险预防和应急响应提供非常有用的信息，从而减轻干旱造成的危害，因而很有必要计算某一严重程度干旱事件发生的平均历时。假设干旱具有s个干旱状态，且序号小的干旱状态表示的干旱严重程度低。则当Tjj+表示干旱严重程度不低于第j个干旱状态的干旱的历时时，Tjj+的发生概率可以计算如下：

(10)

而干旱严重程度不低于第j个干旱状态的干旱的平均历时就是Tjj+的期望，表示为E(Tjj+)。然而对于非均质的马尔科夫链，E(Tjj+)很难通过解析式计算，从而在本文中E(Tjj+)也是通过随机模拟20 000次的方法来计算。

3　结果和讨论

3.1分布函数和Copula函数的选择结果

不同时间尺度的SPEI表征的是不同类型的干旱，对应于农业干旱，3个月时间尺度的SPEI在本文中被用来监测干旱状态。本文分别采用了GNO、GP、P-III、GEV和GLO 分布函数对一年中3个月时间尺度下的各个月的Di序列进行拟合，选择的最优分布函数见表2。从表2可以发现，GEV、GLO和P-III分布函数对大部分站点各月份的Di序列拟合良好。接着根据选好的分布函数，就可以基于等概率转换方法得到SPEI值。

表2　在对3个月尺度下每月的水分亏缺(Di)序列拟合中，具有相同最优分布函数的站点个数

另外根据3个月时间尺度SPEI值(SPEI-3)的定义，可以预期,月SPEI-3会受到前2个月的SPEI-3值的影响，同时本文也对月SPEI-3的自相关系数进行了计算，如图4(a)所示。从图4(a)中可以看出，自相关系数整体上随着通常时滞的增大而减小，而在前2个时滞的自相关性在95%的置信水平内显著。第二时滞的自相关性可能也受第一时滞自相关性的影响，因而本文还对月SPEI-3的部分自相关性系数进行了计算以消除这种干扰,如图4(b)所示。从图4(b)中可以看出，部分自相关性在第一时滞自相关性最强，然后随着时滞的增加逐渐以在正负值之间震荡的方式趋于零。因此，本文认为月SPEI主要受前一个月值的影响，从而用一阶马尔科夫链表示SPEI值的状态转移概率，同时连续2个月的SPEI-3值间的相关性用Copula函数表示。根据2.2部分介绍的Copula拟合优度检验方法，本文选择的最优Copula函数见表3，在用Copula函数对连续2个月相关关系的描述中，具有相同Copula函数的站点个数，其中连续2个月中的第一个月份显示在表3中。从表3中可以看出Gumbel、Gaussian和t Copula函数对连续2个月SPEI-3相关性的描述表现不错。此外，由于月SPEI-3序列是标准正态变量，因而本文中Copula函数的边缘分布为正态分布。

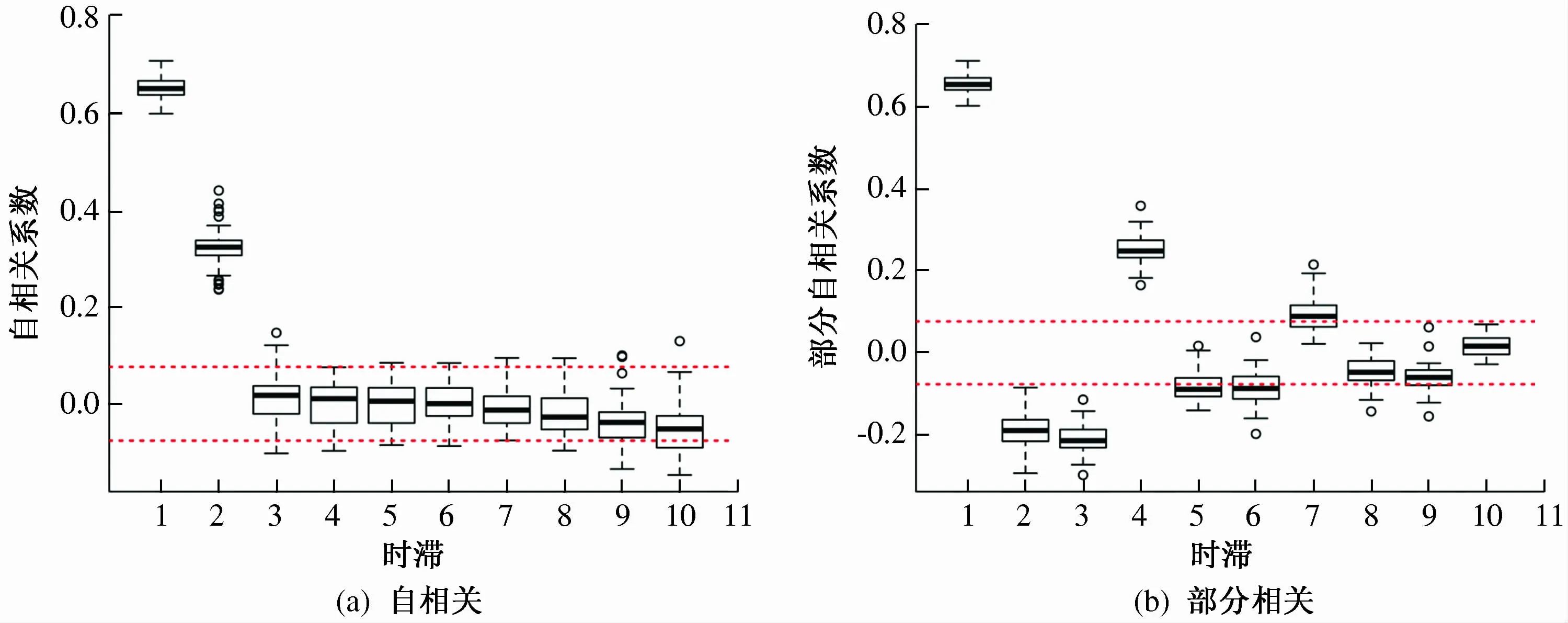
图4　各站点3个月时间尺度SPEI的箱型图(红点线表示的是95%置信区间的阈值)

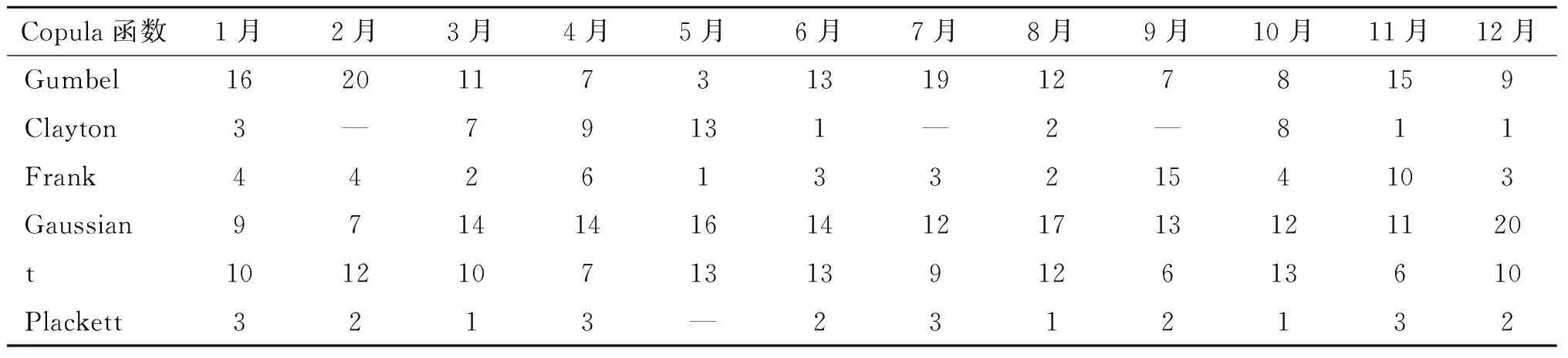
Copula函数1月2月3月4月5月6月7月8月9月10月11月12月Gumbel1620117313191278159Clayton3—79131—2—811Frank44261332154103Gaussian9714141614121713121120t10121071313912613610Plackett3213—2312132

3.2干旱特征的空间分布

通常马尔科夫链的转移概率矩阵是根据观测到的转移样本以最大似然法进行估算的[13, 17]，同样，本文也根据最大似然法对各站点的转移概率矩阵进行了估算。然而由于样本量有限，在某些情况下会得到转移概率为零的情况，见表4。在表1中，本文定义了6种干旱状态(无干旱、D0、D1、D2、D3和D4)，依次表示干旱严重程度从无干旱到非常极端的状态。从表4中可以看出很多站点从D0到D4、D4到D0和D4到无干旱状态的转移概率都为零，这明显是不符合实际的。因而为了避免这种缺陷，本文采用在前文中选好的最优Copula函数从理论上计算各站点各月份的转移概率矩阵。结果发现,对于所有站点，每个月的状态转移概率都是变化的(图5)，因而本文采用的马尔科夫链是非均质的。接着基于这非均质马尔科夫链，对某一严重程度干旱事件的平均历时、从任一干旱状态到没有干旱状态的平均首达时间以及从没有干旱状态到某一严重干旱事件的平均首达时间分别进行了计算。

表4最大似然法估计的转移概率中概率值为0的站点个数

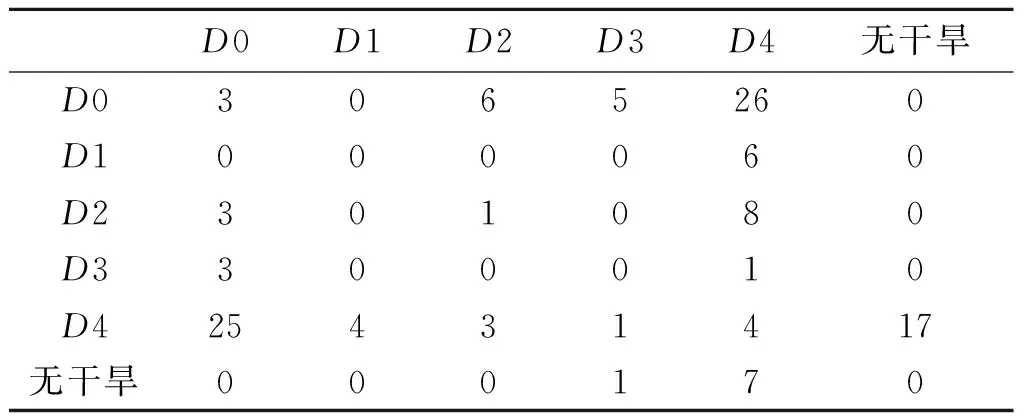
D0D1D2D3D4无干旱D03065260D1000060D2301080D3300010D425431417无干旱000170

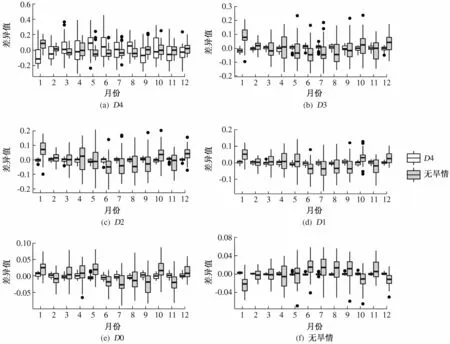
图5　珠江流域各站点从任何干旱状态到D4状态和无旱情状态的各月转移概率变化情况

通过反距离权重插值方法，分析了干旱平均历时的空间分布情况，如图6所示。从图6中可以看出，珠江流域非常极端干旱的平均历时约1.5个月，轻微干旱的平均历时约3个月，这些结果将会为珠江流域的干旱预防和应急管理提供有用的信息。同时，从图6中可以看到珠江流域东南部干旱的平均历时更长，尤其是极端干旱。图7给出了从任一干旱状态到无干旱状态的平均首达时间在珠江流域的空间分布，从图中也发现，珠江流域东南部从干旱状态到无旱情状态的平均首达时间更长。这些说明珠江流域东南部遭受干旱的概率更高，这也与我们之前的文章得到的珠江流域东南部干旱风险更高的结果一致[6, 11]。珠江流域东南部作为一个人口密集、经济发达的区域，高发的干旱风险将会对该区域社会经济的可持续发展造成严重的影响，尤其是对珠三角地区，因而需引起高度重视。类似的，从图6—7中可以看出珠江流域的西部地区也是一个干旱风险高的地区。

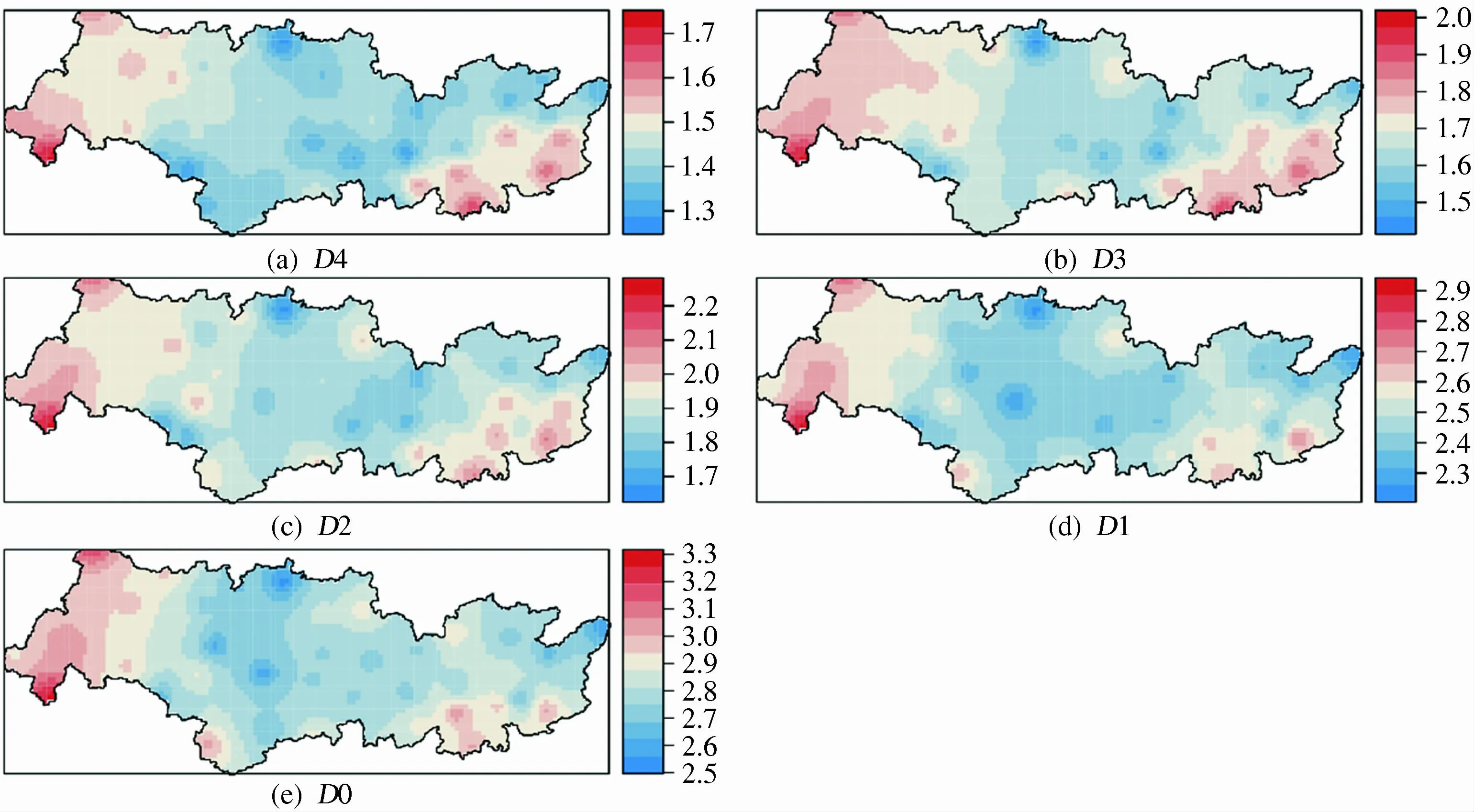
图6　某一严重程度干旱的平均历时在珠江流域的空间分布图(图中颜色条的单位是月)

图7　从任一干旱状态到达无干旱状态的平均首达时间在珠江流域的空间分布图(图中颜色条的单位是月)

从无干旱状态到某一严重干旱事件的平均首达时间的空间分布情况如图8所示。从图8中可看出，整体上看,从无干旱状态到某一严重干旱事件在珠江流域的平均首达时间对于中等干旱是0.5 a、严重干旱是1 a、极端干旱是1.5 a、非常极端干旱是3.5 a。同时，珠江流域上游地区干旱的发生率更高，这进一步增加了珠江流域西部地区的干旱风险。另外，珠江流域东南部和西部的干旱一旦发生，它们将持续更长时间(图6—8)。综合上述所有干旱特征信息，可以更好地了解珠江流域各地区的干旱变化情况，从而为水资源的管理和决策提供参考信息。

图8　从无干旱状态到达某一严重程度干旱的平均首达时间在珠江流域的空间分布图(图中颜色条的单位是月)

4　结　语

很多计算发现由于样本量有限，在某些情况下会导致根据最大似然法计算出的转移概率为零，这是非常不合理的。为了避免传统最大似然估计方法的缺陷，本文介绍了一种用Copula函数计算各月转移概率矩阵的方法，同时由于计算出的转移概率是随时间变化的，因而采用的马尔科夫链是非均质的。接着，根据计算出的非均质马尔科夫链，以珠江流域为研究对象，对某一严重程度干旱事件的平均历时、从任一干旱状态到没有干旱状态的平均首达时间以及从没有干旱状态到某一严重干旱事件的平均首达时间3个干旱特征分别进行了分析。结果发现：①非常极端干旱事件持续约1.5个月，轻微干旱事件持续约3个月；②从非常极端干旱状态恢复到无干旱状态需要约3.5个月时间，而从轻微干旱状态恢复到无旱情需要约1.7个月的时间；③一般来说，珠江流域平均0.5 a中发生一次中等干旱事件，1 a中发生一次严重干旱事件，1.5 a中发生一次极端干旱事件，以及3.5 a中发生一次非常极端干旱事件。这些信息将会对珠江流域的干旱灾害预防及应急管理提供非常有用的信息。此外，研究结果还表明，珠江流域东南部地区干旱风险较高，而该地区人口稠密、经济发达，特别是其中的珠三角地区，因而需要加强对该地区的干旱风险评估和管理。同时，珠江流域西部地区也是干旱风险较高的区域。

[1]Mishra A K,Singh V P.A review of drought concepts[J].Journal of Hydrology,2010,391(2):202-216.

[2]Devereux S.The impact of droughts and floods on food security and policy options to alleviate negative effects[J].Agricultural Economics,2007,37(1):47-58.

[3]Zhang Q,Sun P,Li J F,et al.Spatiotemporal properties of droughts and related impacts on agriculture in Xinjiang, China[J].International Journal of Climatology,2015,35(7):1254-1266.

[4]Wilhite D A.Drought as a natural hazard:concepts and definitions[M]//Drought:A Global Assessment[M].London:Routledge Publishers,2000:3-18.

[5]Vörösmarty C J,Green P,Salisbury J,et al.Global water resources:vulnerability from climate change and population growth[J].Science,2000,289:284-288.

[6]Zhang Q,Xiao M Z,Singh V P,et al.Regionalization and spatial changing properties of droughts across the Pearl River basin,China[J].Journal of Hydrology,2012,472-473:355-366.

[7]Kao S C,Govindaraju R S.A copula-based joint deficit index for droughts[J].Journal of Hydrology,2010,380(1-2):121-134.

[8]Shiau J.Fitting drought duration and severity with two-dimensional copulas[J].Water Resources Management,2006,20(5):795-815.

[9]Zhang Q,Xiao M Z,Singh V,et al.Copula-based risk evaluation of hydrological droughts in the East River basin,China[J].Stochastic Environmental Research and Risk Assessment,2013,27(6):1397-1406.

[10]Loukas A,Vasiliades L.Probabilistic analysis of drought spatiotemporal characteristics in Thessaly region,Greece[J].Natural Hazards and Earth System Science,2004,4:719-731.

[11]肖名忠,张强,陈晓宏.基于多变量概率分析的珠江流域干旱特征研究 [J].地理学报,2012,67(1):83-92.

[12]Cancelliere A,Mauro G D,Bonaccorso B,et al.Drought forecasting using the standardized precipitation index [J].Water Resources Management,2007,21(5):801-819.

[13]Sanusi W,Jemain A,Zin W,et al.The drought characteristics using the first-order homogeneous markov chain of monthly rainfall data in peninsular malaysia[J].Water Resources Management,2015,29(5):1523-1539.

[14]Vicente-Serrano S M,Beguer A S,López-moreno J I.A multiscalar drought index sensitive to global warming:The standardized precipitation evapotranspiration index[J].Journal of Climate,2010,23(7):1696-1718.

[15]Yu M,Li Q,Hayes M J,et al.Are droughts becoming more frequent or severe in China based on the standardized precipitation evapotranspiration index:1951—2010? [J].International Journal of Climatology,2014,34(3):545-558.

[16]Zhang Q,Qi T Y,Singh V P,et al.Regional frequency analysis of droughts in China:multivariate perspective[J].Water Resources Management,2015,29(6):1767-1787.

[17]Paulo A,Pereira L S.Prediction of SPI drought class transitions using markov chains[J].Water Resources Management,2007,21(10):1813-1827.

[18]Madadgar S,Moradkhani H.A bayesian framework for probabilistic seasonal drought forecasting[J].Journal of Hydrometeorology,2013,14(6):1685-1705.

[19]Yang T,Shao Q,Hao Z C,et al.Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin,China[J].Journal of Hydrology,2010,380(3-4):386-405.

[20]Wong J S,Zhang Q,Chen Y D.Statistical modeling of daily urban water consumption in Hong Kong:trend,changing patterns,and forecast[J].Water Resources Research,2010,46(3):W03506.

[21]Droogers P,Allen R.Estimating reference evapotranspiration under inaccurate data conditions[J].Irrigation and Drainage Systems,2002,16(1):33-45.

[22]Hargreaves G H.Defining and using reference evapotranspiration[J].Journal of Irrigation and Drainage Engineering,1994,120(6):1132-1139.

[23]Beguer A S,Vicente-Serrano S M.SPEI:Calculation of the Standardised Precipitation-Evapotranspiration Index[R/OL].[2015-01-20].http://CRAN.R-project.org/package=SPEI.

[24]Mckee T B,Doesken N J,KLEIST J.The relationship of drought frequency and duration to time scales[C]//Proceedings of the Proc Eighth Conf on Applied Climatology.Amer.Meteor.Soc.Anaheim,CA,F:1993.

[25]Hosking J R M.L-moments:analysis and estimation of distributions using linear combinations of order statistics[J].Journal of the Royal Statistical Society Series B (Methodological),1990,52(1):105-124.

[26]Madadgar S,Moradkhani H.Spatio-temporal drought forecasting within Bayesian networks[J].Journal of Hydrology,2014,512:134-146.

[27]Chen Y D,Zhang Q,Xiao M Z,et al.Probabilistic forecasting of seasonal droughts in the Pearl River basin,China[J/OL].Stochastic Environmental Research and Risk Assessment,2015:1-10(2015-11-20)[2015-10-24].http:∥link.springer.com/journal/477.DOI：10.1007/s00477-015-1174-6.

[28]Nelsen R B.An Introduction to Copulas[M].New York:Springer Verlag,2006.

[29]Genest C,R Millard B,Beaudoin D.Goodness-of-fit tests for copulas:a review and a power study[J].Insurance:Mathematics and Economics,2009,44(2):199-213.

[30]Hofert M,Kojadinovic I,Maechler M,et al.Copula:Multivariate Dependence with Copulas[R/OL].[2015-10-24].http:∥CRAN.R-project.org/package=copula.

(责任编辑：蔡洪涛)

Research on Drought Behaviors in the Pearl River Basin Based on Markov Chain

XIAO Mingzhong1, 2, ZHANG Qiang1, 2, KONG Dongdong1, 2, ZHANG Zhenghao1, 2

(1. Department of Water Resources and Environment, Sun Yat-sen University, Guangzhou 510275, China;2. Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong High Education Institute,Sun Yat-sen University, Guangzhou 510275, China)

Deep understanding of transition probability behaviors of droughts is the key to forecast of droughts, and mitigation of drought hazards. In this case, the transition probability matrix of the Markov chain was derived by the Copula functions. Six drought status were classified in the study, drought event was different from drought status, and a drought event with the severity not less than a certain drought status had been considered as a certain severe drought. In order to investigate the drought behaviors in the Pearl River basin, the mean duration of a certain severe drought, the mean first passage time from any drought status to no drought status, and the mean first passage time from no drought status to a certain severe drought were analyzed in this study. The results of this study indicated that: (1) the exceptional drought event lasted about 1.5 months, and the mild drought event lasted about 3 months; (2) it took about 3.5 months from the exceptional drought status to no drought status, while it took about 1.7 months from the mild drought status to no drought status; (3) generally, and there was a moderate drought event average in 0.5 years, a severe drought event in 1 year, an extreme drought event in 1.5 years, and an exceptional drought event in 3.5 years. Further, the results of this study indicated higher risk of drought in the southeast part of the Pearl River basin, and further works needed to be done to prevent or mitigate the drought hazards, as these regions were densely populated and economically developed, especially in the Pearl River delta. In addition, the west part of the Pearl River basin had also been identified as a region with a higher risk of drought.

drought; Markov chain; copula functions; transition probability; standardized precipitation evapotranspiration index (SPEI)

2015-12-20

国家杰出青年科学基金项目(51425903)；香港特别行政区研究资助局项目(CUHK441313)；中央高校基本科研业务费专项资金联合资助。

肖名忠(1990—)，男，江西吉安人，博士，主要从事气象水文极值分析方面的研究。E-mail:xmingzh@mail2.sysu.edu.cn。

张强(1974—)，男，山东沂水人，教授，博士生导师，博士，主要从事流域气象水文学、旱涝灾害机理、流域地表水文过程及其对气候变化的响应机制与机理以及流域生态需水等领域的研究。E-mail:zhangq68@mail.sysu.edu.cn。

10.3969/j.issn.1002-5634.2016.01.003

TV882.4;P333

A

1002-5634(2016)01-0015-09