抛物面镜球面波反射声场特性的理论研究
张 军,陈 鹏,陈正武,赵 云,曾新吾
(1.中国空气动力研究与发展中心 气动噪声控制重点实验室,四川 绵阳 621000;2.国防科学技术大学 光电科学与工程学院,长沙 410073)
抛物面镜球面波反射声场特性的理论研究
张军1,陈鹏1,陈正武1,赵云2,曾新吾2
(1.中国空气动力研究与发展中心 气动噪声控制重点实验室,四川 绵阳621000;2.国防科学技术大学 光电科学与工程学院,长沙410073)
根据Kirchhoff-Helmholtz声衍射理论,独立推导了沿抛物面镜轴线的球面波反射声场的时域理论解。基于理论解预测近场反射波中存在三种子波,即“中心波”、“边缘波”和“尾波”,中心波的相位与边缘波和尾波相反。远场反射波与声源波形的导数形式相同,声压幅值和传播距离成反比而与声波频率成正比。以典型的正弦波为例给出了反射声场的演化形成过程,并通过COMSOL软件进行数值模拟验证了三种子波的存在及理论解的正确性。最后研究了球面波反射声场的特性,如果抛物面镜的口径固定,则存在一个最优的深焦比参数d/zF=3.92使得远场的反射波声功率密度最大。
抛物面镜;球面声波;反射声场
抛物面镜具有特殊的几何性质,平行射线经抛物面反射后将会聚焦或者从焦点发出的射线经抛物面反射后将成为平行射线。因此,抛物面镜多被用作信号的接收器或发射器,例如在工程上常使用抛物面天线来接收电磁波信号以提高信噪比,或者将抛物面镜作为高能激光的中继镜以提高机载激光器的传输距离[1]。在声学领域,抛物面镜本质上属于一种曲面声障板,常规换能器使用声障板可以提高声波的发射效率。与相控阵技术相比,声障板的方法易于实现且成本更低。张军等[2]研究了电弧放电式等离子体声源(Plasma Sound Source)的聚焦原理,指出椭球面镜虽可以将球面波由近焦点聚焦到远焦区域,但是在过远焦点之后声能量的衰减非常迅速。所以椭球面镜聚焦系统适合用于治疗人体结石等对传输距离要求不高的场合,而要在较远的距离上提高声学换能器的发射效率则需要使用抛物面镜。
王鸿樟[3]使用抛物面镜作为声反射障板提高了聚焦换能器的发射效率,他利用频域Kirchhoff公式推导了一个发射声压的表达式。WAHLSTROM[4]使用一个传声器和抛物面镜,从远处成功接收到了生物类声源的声信号。他在平面波入射条件下建立了抛物面镜的线性声波反射模型,推导了反射声场的频域解析解,并据此研究了反射声场的特性。DAI等[5]使用抛物面镜作为接收器提高了S1型-零群速度(S1ZGV)兰姆波的信噪比,S1ZGV兰姆波在薄板中很容易被激发,因此其常被用于超声无损检测。后来TSAI等[6-7]推导了平面波及轴对称非平面波入射条件下抛物面镜反射声场的时域理论解,讨论了抛物面镜几何参数及入射波频率参数变化对反射声场的影响。王鸿樟和Wahlstrom得到的都是频域结果,而Tsai等人得到的是时域结果。与频域结果相比,时域结果具有以下优点:一是可以更清楚的揭示声场形成过程;二是受声波的频带范围限制小。本文根据Kirchhoff-Helmholtz声衍射理论,独立推导了抛物面镜球面波反射声场的时域理论解,建立了将抛物面镜作为声发射器的时域理论方法,从而完善了王鸿樟等的理论研究。
本文的内容分为四个部分:第一节建立了抛物面镜球面波反射的理论模型,并给出了反射声场沿抛物面镜轴线的解析解和远场解;第二节以正弦波为例给出了沿抛物面镜轴线的反射声场的形成过程;第三节利用多物理场有限元软件COMSOL进行了数值模拟,验证了理论结果的正确性;第四节研究了抛物面镜反射声场的特性,讨论了开角和深焦比等参数对反射声场的影响。
1 理论
从抛物面镜焦点发出的球面波在传播过程中将分成两个部分,一部分仍按球面波形式扩散,另一部分入射到壁面后发生反射。根据惠更斯原理,反射波可以视为新的次级波源,次级波相干叠加便形成了反射声场。因此空间中的声场包含直达波和反射波。本文主要研究球面波的反射声场。如图1所示,从焦点发出的射线经抛物面镜反射后将成为平行于其轴线的射线。
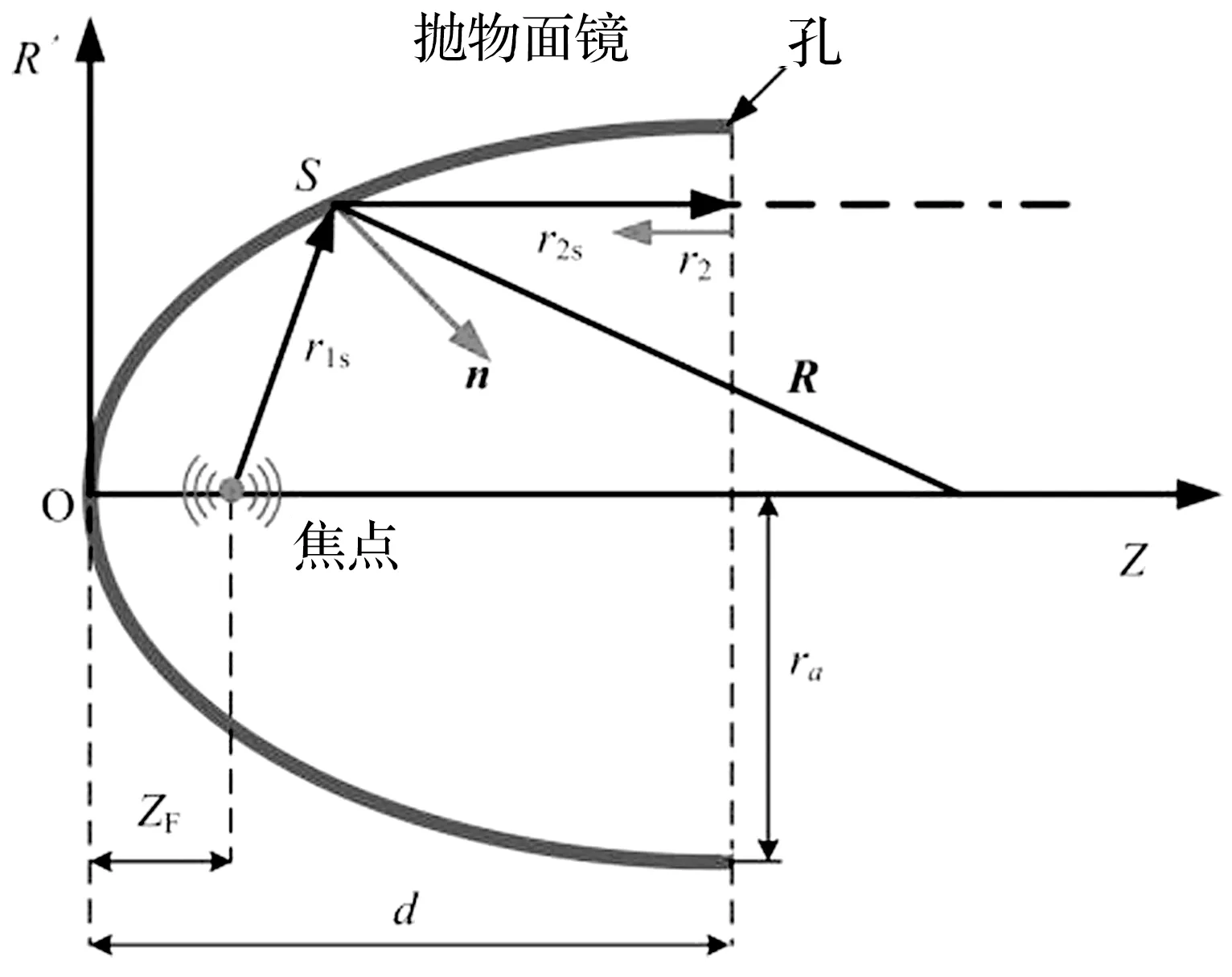
图1 抛物面镜球面波反射的几何示意图Fig.1 The reflection of a spherical wave from a parabolic mirror
在直角坐标系下,旋转抛物面的方程可以表示为,
(1)
式中:(x,y,z)中的下标s代表“Surface”,表示位于抛物面镜上的点。R’代表x坐标或y坐标,zF表示抛物面镜顶点到焦点之间的距离,即焦距;d表示抛物面镜顶点到开口的距离,即深度;S为抛物面镜上的一点,r1s=zs+zF为焦点到S之间的距离;r2s=d-zs为S到抛物面镜开口之间的固定距离;r2为抛物面镜开口到 r2s上任意一点之间的变化的距离。R为点S与抛物面镜轴线上一点P之间的距离,n表示点S处垂直于抛物面镜表面的内法线方向单位向量。
假设传播介质无耗散、各向均匀,Gold’berg数(即非线性系数与耗散系数之比)小于1,则声波的传播由线性波动方程控制。
(2)
式中,c0表示介质中的声速。
根据封闭空间中的能流守恒原理,若已知封闭面上的声场的分布则可得到封闭面内任意一点处的声场[8]。忽略封闭面上二次以上的声反射,由式(2)可以得到非单色波的Kirchhoff-Helmholtz时域一般解。
(3)
Kirchhoff-Helmholtz公式是基于衍射理论的一般解,对具有波动特性的波(如光波、声波)的传播都适用。为了便于书写,式(3)省略了物理量的时间变量和空间变量。其中,p表示目标点处的反射声压,pg表示通过射线声学得到的封闭面上的声压。∂/∂n表示沿抛物面内法线方向的方向导数,S表示由抛物面镜和从抛物面镜出口到无穷远处的假想曲面组成的封闭面。“[·]”是一种记号,表示其中的物理量经历了R/c0的时间延迟。根据Somerfield辐射条件[9],可以忽略从无穷远处来的声场的贡献,式(3)的积分只在抛物面上进行。
2.1边界条件
假设声波的波长与抛物面镜的曲率半径相比很小(ka≫1,k表示波数,a表示曲率半径),则射线声学的理论可用于声场计算。球面波声压与传播距离r之间有如下关系
(4)
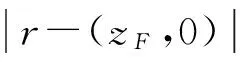
(5)

(6)
在镜面上一点S处,可以得到如下的边界条件,
(7)
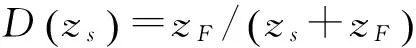
(8)
式中:ρ=0表示抛物面镜开口圆的中心点,ρ=1表示边缘点。可以发现,固定焦距,随着抛物面镜深度d增加反射波的压力幅值减小。因为深度d增加将使得从焦点zF处发出的球面波到达相同镜面点所经历的传播距离延长,而球面波的声压幅值与传播距离成反比。
2.2沿抛物面镜轴线球面波反射声场的理论解
边界条件式(7)包含了任意形式的源函数f(t),f(t)在积分过程中难以处理。根据线性系统理论,系统的输出可以通过输入函数与系统的冲击响应函数相卷积得到。可以利用冲击函数δ(t)代替f(t)先求解系统的冲击响应函数h(t),然后通过h(t)与f(t)相卷积便可以得到反射声场的解。边界条件(7)相应改写为,
(9)
结合抛物面镜方程式(1),经过繁杂的数学推导得到了冲击响应函数。
(10)
式(10)右端各项的表达式如下
(11)
进一步通过卷积便可以得到沿抛物面镜轴线任意位置处的反射声场的解。
(12)
式(12)右端包含三项,分别对应从抛物面镜顶点、出口边缘和其余表面发出的反射波。根据Blackstocks[10]及Hamilton[7],本文将其称为“中心波”、“边缘波”和“尾波”。从声波的相位来看,边缘波和尾波的相位与中心波是相反的。
2.3远场解
随着观察点远离抛物面镜,中心反射波和边缘反射波的到达时间差缩短,于是尾波项的积分时间趋近于0,尾波趋近于δ脉冲。在远场(z/zF≫1),式(12)退化为更加简单的形式,
(13)
根据式(13),远场反射波将退化为声源波形的导数形式,例如从抛物面镜焦点处发出的正弦波在远场将退化为余弦波。当抛物面镜深度远小于焦距时,上式与圆形平面活塞声源的远场解形式上一致[11]。不难发现,抛物面镜远场反射声压主要受几何参数(d/zF)及声源波形参数(df/dt)控制。定义远场反射波的声压幅值与p0之比为抛物面镜的远场增益,当焦距固定而深度变化时有如下关系

(14)
当抛物面镜的口径固定而深焦比变化时,

(15)
对于简谐变化的声波,df(t)/dt~jω,则有
(16)
式中:λ=2πc0/ω为声波的波长,ω为声波的角频率。可以发现,远场增益G3与声波的波长λ成反比,但由于实际介质中存在黏性和热传导耗散,高频声波更容易被吸收。
2 反射声场的形成过程
下面以正弦波为例研究反射声场的形成过程。取抛物面镜的焦距zF=0.05 m,深度d=0.2 m;抛物面镜的口径ra=0.2 m。将球面波声源置于抛物面镜的焦点处。距离焦点r=zF处的球面波压力幅值为P0,单个周期正弦波脉冲的持续时间T0=0.1 ms;传播介质为空气,密度ρ0=1.25 kg/m3,声速c0=340 m/s。计算结果如图2所示。
图2(a)为输入的正弦波,图2(b)~2(f)为沿抛物面镜轴线的反射波计算结果。根据反射波形特点,可以将反射声场分为近场和远场两个区域:当反射波形与初始波形的导数形式相同时表明观察点到达远场区。当抛物面镜的深焦比d/zF较小时,近场和远场的临界距离为平面活塞声源的瑞利距离(lR=πa2/λ)[11]。

图2 抛物面镜轴线上球面波反射声场的形成过程Fig.2 The evolution ofan on-axis sinusoidal waveform
在近场区,反射波形包含中心波“C”、边缘波“E”和尾波“W”等复杂的波形结构(见图2(b)~2(c))。在到达观察点的时间顺序上,边缘波滞后于中心波,“尾波”夹在中心波和边缘波之间。根据几何关系,当深焦比d/zF较大时,边缘波的传播距离大于中心波的传播距离,因此其达到时间也越晚。随着距离增加,中心波和边缘波到达观察点的时间差将缩短。在幅值关系上,中心波比边缘波大,两者之间的关系受抛物面镜的深焦比参数控制。深焦比越大,边缘波的幅值越小。
在远场区,中心波、边缘波和尾波将叠加在一起,反射波演化成声源波形的导数形式。根据式(13),远场反射波的声压幅值与传播距离成反比。反射波的声压幅值随距离增加下降较快。这在反射声束上体现了一种“近场集中,远场发散”的特性。显然,这是由声波的衍射效应引起的,频率越低声衍射效应越明显。这种性质在具有波动性的光波和电磁波中也存在,例如手电筒发出的准直光束到了较远距离处就逐渐发散了。尽管如此,在100倍焦距处,本算例的反射波聚焦增益超过了20 dB。
3 数值模拟验证
王鸿樟等人的研究结果无法与本文的研究结果直接进行对比,本节使用多物理场有限元软件COMSOL对抛物面镜的声波反射过程进行了模拟,希望通过模拟结果对推导结果进行数值验证。
COMSOL软件包含了声学、流体力学、结构力学等多个求解模块,该软件的优点是可以有效求解多个物理场的耦合问题。COMSOL的求解包括物理场选择、几何建模、网格划分、求解器配置和结果后处理等几个步骤。COMSOL软件已由最初的3.X版本发展到了目前的5.X版本,本文使用的是5.0版本。首先选择瞬态压力声学模型,并建立起简化的二维轴对称几何模型,如图3所示。
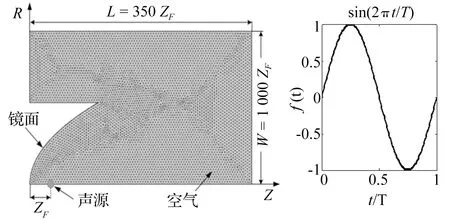
图3 COMSOL软件中建立的几何模型和声源输入Fig.3 The geometric model of a parabolic mirror in COMSOL
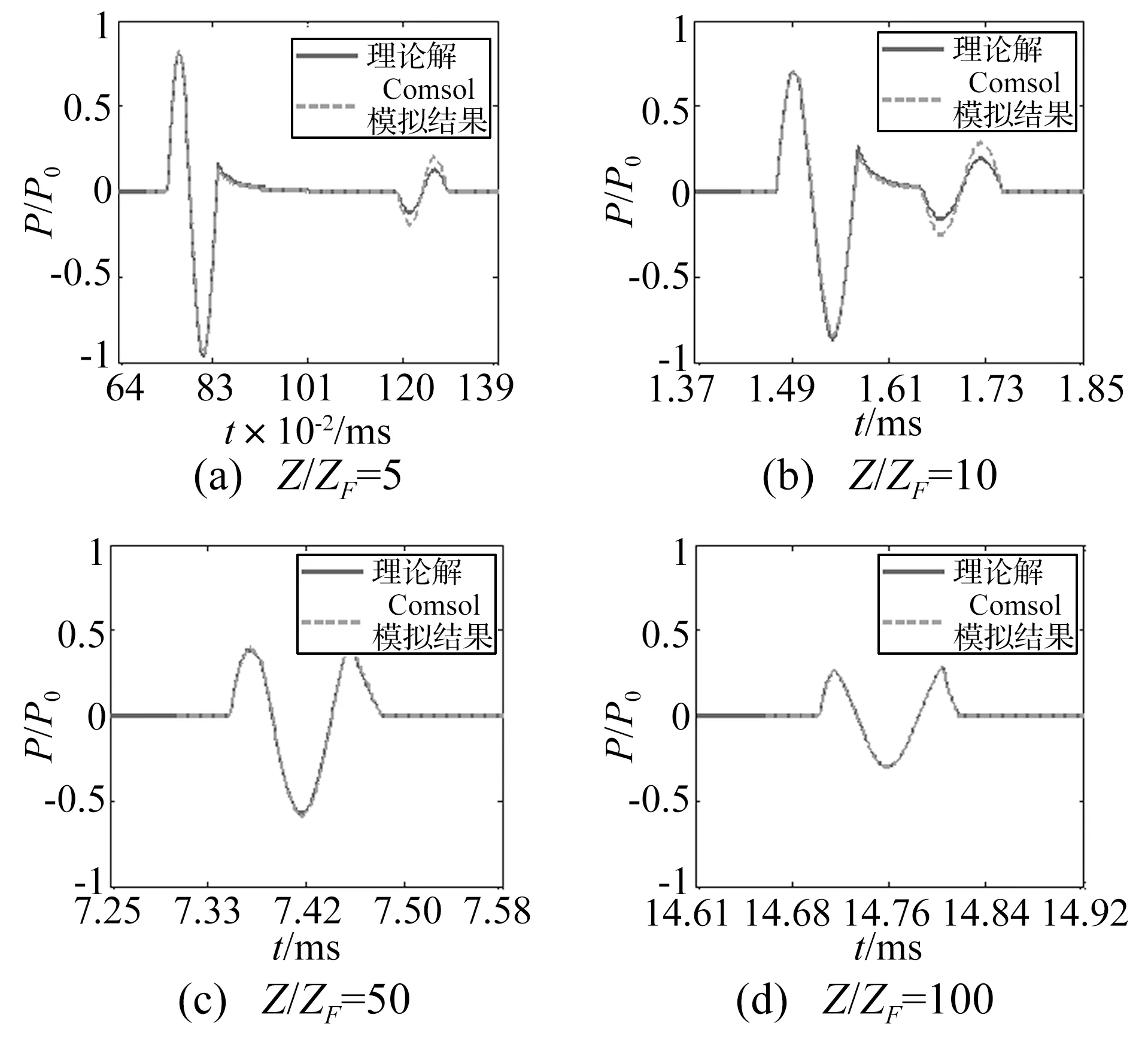
几何模型由参数化曲线(y2=4zFx)和贝氏曲线转化成的实体区域组成。区域内的材料为空气,材料参数使用软件内置参数,区域的边界采用刚性边界条件,区域的总体尺寸如图3所示。网格划分采用自由三角形网格,最大网格尺寸hmax为声波波长的1/6。最大网格尺寸和时间步长之间满足CFL稳定性条件,即tstep=CFL*hmax/Cair,CFL=0.05。声源设置在抛物面镜的焦点上,声源波形为单个周期的正弦波f=Asin(f0*t)*(t 图4给出了单个周期的正弦波在四个不同时刻的二维传播云图。 图4 不同传播时刻正弦波的二维云图Fig.4 Snapshots of a sinusoidal wave at different times 图4(a),在t1=0.15 ms时刻从焦点发出的球面波的波阵面正好达到抛物面镜的顶点。图4(b),t2=0.45 ms时刻声场分成了三个部分:以球面波形式向前传播的直达波“D”,反射中心波“C”,以及镜面附近的反射尾波“W”。中心波的声压幅值高于直达波和尾波。可以发现,球面波经抛物面镜反射后变成了准直平面波。图4(c),在t3=0.9 ms时刻反射中心波之后出现了边缘波E。边缘波起源于抛物面镜的开口边缘,在直达波到达镜面边缘的时刻产生,并以边缘点为中心按球面波的形式扩散。在向抛物面镜轴线方向的传播汇聚过程中,边缘波的相位和中心波相反。尾波的幅值较小,云图中难以看出尾波的存在。图4(d),在t4=1.05 ms时刻可以清楚的看出中心波和边缘波的传播情况。根据模拟结果,理论预测的近场三种子波确实是存在的。 假设单个周期正弦波的持续时间T=0.1 ms,即声波的中心频率f0=10 kHz。按照文献[6]中的计算方法得到ka=19,表明声波在镜面附近的反射可以使用射线理论求解。沿抛物面镜轴线z/zF=5,10,50,100将理论解和软件的模拟结果进行对比,如图5所示。 图5 COMSOL软件模拟结果与理论解的对比Fig.5 Results of the present solution and COMSOL simulation 图5中蓝色实线代表理论解,红色虚线代表使用COMSOL软件得到的模拟结果。可以发现,理论解的中心波和COMSOL的模拟结果之间符合得很好,而理论解的边缘波幅值比模拟结果略小。两者之间的差异可能是由网格剖分在抛物面镜边缘处不细致引起的。对有限元软件而言,网格剖分的好坏将直接影响计算结果。对于远场反射波,理论解和COMSOL模拟结果之间符合得非常好。从而通过数值模拟方法使第二节的理论解的正确性得到了验证。 反射镜的形状主要由深焦比d/zF或开角θ等参数控制。θ是由焦点与抛物面镜出口边缘的连线与轴线之间组成的夹角, (16) 当θ=90°时,抛物面镜的焦点正好位于出口面上。如果焦距固定而深焦比增加,则抛物面镜的口径和开角也增加;如果口径固定,则随深度变小开角也变小。 分别将抛物面镜的焦距和口径固定,远场增益随深焦比的变化如图6所示。固定抛物面镜焦距,远场增益将随深度的增加而缓慢增加,这是因为深度增加将使得更多的声线受到抛物面镜的反射。固定抛物面镜口径,则存在一个最优的深焦比参数d/zF=3.92使得远场增益达到最大值。Wahlstrom在平面波入射条件下也得到了一个相同的深焦比参数,使得抛物面镜焦点处的反射声压达到最大值[3]。不难理解,这正是线性条件下声波的传播满足互易原理的体现。 图6 远场增益与深焦比的关系Fig.6 The relationship between depth-to-focal-length ratio and far field gain 取焦距zF=0.05 m,单个周期正弦波的持续时间分别为T1=0.1 ms和T2=0.02 ms,抛物面镜的开角θ分别为60°,90°,120°和150°。根据式(12)和(17),得到反射波的声功率密度的变化,如图7所示。 图7 不同开角,抛物面镜轴线上声功率密度的变化Fig.7 The relationship between on-axis sound power density and axial propagation distance with different rim angles 由图7可见,反射波的声功率密度随传播距离呈现先增加而后减小的趋势,这是因为反射波形的演化使得抛物面镜的轴线上存在这样一个特殊的观察点:在该点之前,中心波和边缘波是分离的(见图2(b)、2(c));在该点处,中心波的负压部分和边缘波的负压部分恰好完全重叠而使得声信号的负压幅值达到极大;在该点之后,中心波的正压部分与边缘波的负压部分或中心波的负压部分与边缘波的正压部分重合使得有效声压的幅值减小。满足远场条件后,反射波演化为声源波形的导数形式,声压幅值与传播距离成反比。 从图7中可以看出,随着抛物面镜开角增大,远场反射波的声功率密度也越大。因为开角增加,抛物面镜的深焦比d/zF也增加,这就相当于使抛物面镜的焦点向底部移动,使得更多的声线受到镜面的反射并使得远场的反射波声功率密度增加。抛物面镜开角增大,近场反射波的声功率密度反而减小。其原因在于:当开角较小(θ<90°)时,抛物面镜较“浅”,焦点位于开口面之外。此时从焦点发出的球面波到达抛物面镜顶点和边缘点的声程差很小,反射中心波与边缘波的幅值接近,并且两者在达到观察点的时间上较为一致,于是中心波的负压部分与边缘波的负压部分相互叠加形成了与声源波形导数形式相同的波形。如前文所述,这种反射波形对应的声功率是最大的。如果开角增大,焦点向抛物面镜的底部移动,从焦点发出的球面波到达边缘点的声程将比到达顶点的声程大,从而使得边缘波的幅值比中心波的小,并且在到达观察点的时间上边缘波滞后于中心波,于是反射波对应的声功率也逐渐减小。当观察点位于远场时,反射波的传播距离很远,由抛物面镜开角变化引起的声程差可以忽略不计,反射波的波形及声功率的大小遵循式(13)的规律。 在固定的观察点处,本文进一步研究了反射波声功率随抛物面镜深焦比的变化,如图8所示。 图8 抛物面镜反射声场的最优深焦比参数Fig.8 Optimum depth-to-focal-length ratios for the reflection sound of a parabolic mirror 分析结果发现,在抛物面镜轴线上存在一个最优的深焦比参数值使得该处反射波的声功率最大(图8(a))。深焦比参数超过该值,反射波的声功率将出现一定程度的下降。例如,当声波频率f0=100 kHz,抛物面镜焦距zF=0.05 m时,在z/zF=100处最优深焦比参数d/zF=1.4;在z/zF=200处时,最优深焦比参数d/zF=2.6。上述最优深焦比参数对于抛物面镜的设计具有实际意义,它可以避免在设定传播距离上将抛物面镜设计得过大。随之我们计算了不同观察点处的最优深焦比参数(图8(b)),发现最优深焦比参数与传播距离之间呈线性关系。并且随着声信号频率的升高,最优深焦比参数曲线的斜率减小。这说明对于高频声波不需要将抛物面镜设计得过大;而对于低频声波,想要提高换能器的发射效率则需要将抛物面镜设计得很大。 工程上使用抛物面镜可提高换能器的发射效率。假设声波波长与抛物面镜的曲率半径相比很小,传播介质无耗散、各向均匀,首先根据Kirchhoff-Helmholtz声衍射理论独立推导了沿抛物面镜轴线球面波反射声场的时域理论解,预测近场反射波包含 “中心波”、“边缘波”和“尾波”,中心波的相位与边缘波和尾波相反。远场反射波的波形与声源波形的导数形式相同,声压幅值与传播距离成反比而与声波的频率成正比。理论解的正确性得到了COMSOL软件数值模拟的验证。其次,以单个周期的正弦波为例分析了反射声场的形成过程。最后,基于推导的理论结果研究了球面波反射声场的特性,讨论了抛物面镜开角和深焦比参数对反射声场的影响。开角越大,远场反射波的声功率越大而近场反射波的声功率越小。固定抛物面镜的口径,则存在一个最优的深焦比参数d/zF=3.92使得远场反射波声功率最大。固定抛物面镜的焦距,在特定传播距离上也存在一个最优的深焦比参数值。该值与传播距离之间成线性关系,并且随声波频率的变化而改变。 [1]吴慧云,吴武明,陈金宝,等.100 kW功率固体激光中继镜系统对1 km高度目标作用效果模拟[J].光学学报,2008,28(10):1967-1970. WU Huiyun,WU Wuming,CHEN Jinbao,et al.Simulation of effect of 100 kW solid-state laser relay mirror system on 1 km altitude target[J].ACTA Optical Sinca,2008,28(10):1967-1970. [2]张军,曾新吾,陈聃,等.水下强声波脉冲负压的产生和空化气泡运动[J].物理学报,2012,18:184302. ZHANG Jun,ZENG Xinwu,CHEN Dan,et al.Generation of negative pressure in water an cavitation bubble dynamics [J].ACTA Physica Sinca,2012,18:184302. [3]王鸿樟.换能器与聚焦系统[M].上海交大出版社,1995,243. [4]WAHLSTROM S.The parabolic reflector as an acoustical amplifier[J].J.Audio Eng.Soc.,1985,33(6):41-429. [5]DAI X,ZHU J,TSAI Y T,et al.Use of parabolic reflector to amplify in-air signals generated during impact-echo testing[J].J.Acoust.Soc.Am.,2011,130:167-172. [6]HAMILTON M F.Transient axial solution for the reflection of a spherical wave from a concave ellipsoidal mirror[J].J.Acoust.Soc.Am.1993,93(3):1256-1266. [7]TSAI Y T,ZHU J,HABERMAN M R.Transient axial solution for plane and axisymmetric waves focused by a paraboloidal reflector[J].J.Acoust.Soc.Am.,2013,133(4):2025-2035. [8]FRANCO E E,ANDRADE M A,ADAMOWSKI J C.Acoustic beam modeling of ultrasonic transducers and arrays using the impulse response and the discrete representation methods[J]J.of the Braz.Soc.of Mech.Sci.& Eng.,2011,33(4):408-416. [9]PIWAKOWSKI B,SBAI K.A new approach to calculate the field radiated from arbitrarily structured transducer arrays[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1999,46(2):422-440. [10]BLACKSTOCK D T,MORFEY C L.Reflection and transmission of spherical waves incident on a concentric spherical interface[J].J.Acoust.Soc.Am.,1991,89:1971. [11]ROBINSON D E,LEES S,BESS L.Near field transient radiation patterns for circular pistons[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1974,22(6):395-403. Reflection sound field’s characteristics for spherical sound wave from a parabolic mirror ZHANG Jun1,CHEN Peng1,CHEN Zhengwu1,ZHAO Yun2,ZENG Xinwu2 (1.Key Laboratory of Aerodynamic Noise Control,China Aerodynamics Research and Development Center,Mianyang 621000,China;2.College of Opto-electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China) Based on Kirchhoff-Helmholtz sound diffraction theory,a transient axial solution to reflection sound field of spherical acoustic wave from a parabolic mirror was derived.It was assumed that the spherical ware’s wavelength be small compared to the dimensions of the mirror and the geometric acoustic theory could be applied.The theoretical solution indicated that the near field reflection wave consists of three parts,i.e.,center wave,edge wave and wake wave; the phase of the center wave is opposite to those of the edge wave and wake one; the wave form of the far field reflection wave is consistent with that of the derivative of the sound source wave,and its sound pressure amplitude is inversely proportion to propagation distance and direct proportion to frequency.Taking a sinusoidal wave as an example,evolution and formation processes of its reflection sound field were presented.The existence of three wavelets and the correctness of the theoretical solution were verified with simulations using the software COMSOL.Lastly,the characteristics of the reflection sound field were studied,and the effects of geometric parameters of the mirror on the characteristics were discussed.It was shown that if the aperture of the mirror is fixed,an optimal depth-to-focal-length ratio d/zF=3.92 exists to maximize the sound power density of the far field reflection wave. parabolic mirror; spherical sound wave; reflection sound field 国家自然科学基金(11504417;11172007) 2015-02-11修改稿收到日期:2015-08-06 张军 男,博士,助理研究员,1983年11月生 曾新吾 男,教授,博士生导师,1963年4月生 TB54 A DOI:10.13465/j.cnki.jvs.2016.17.022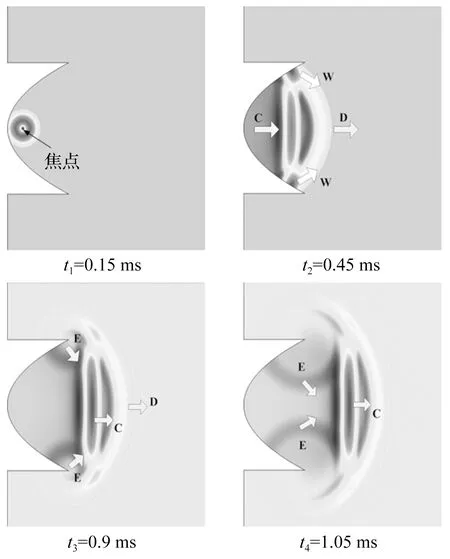
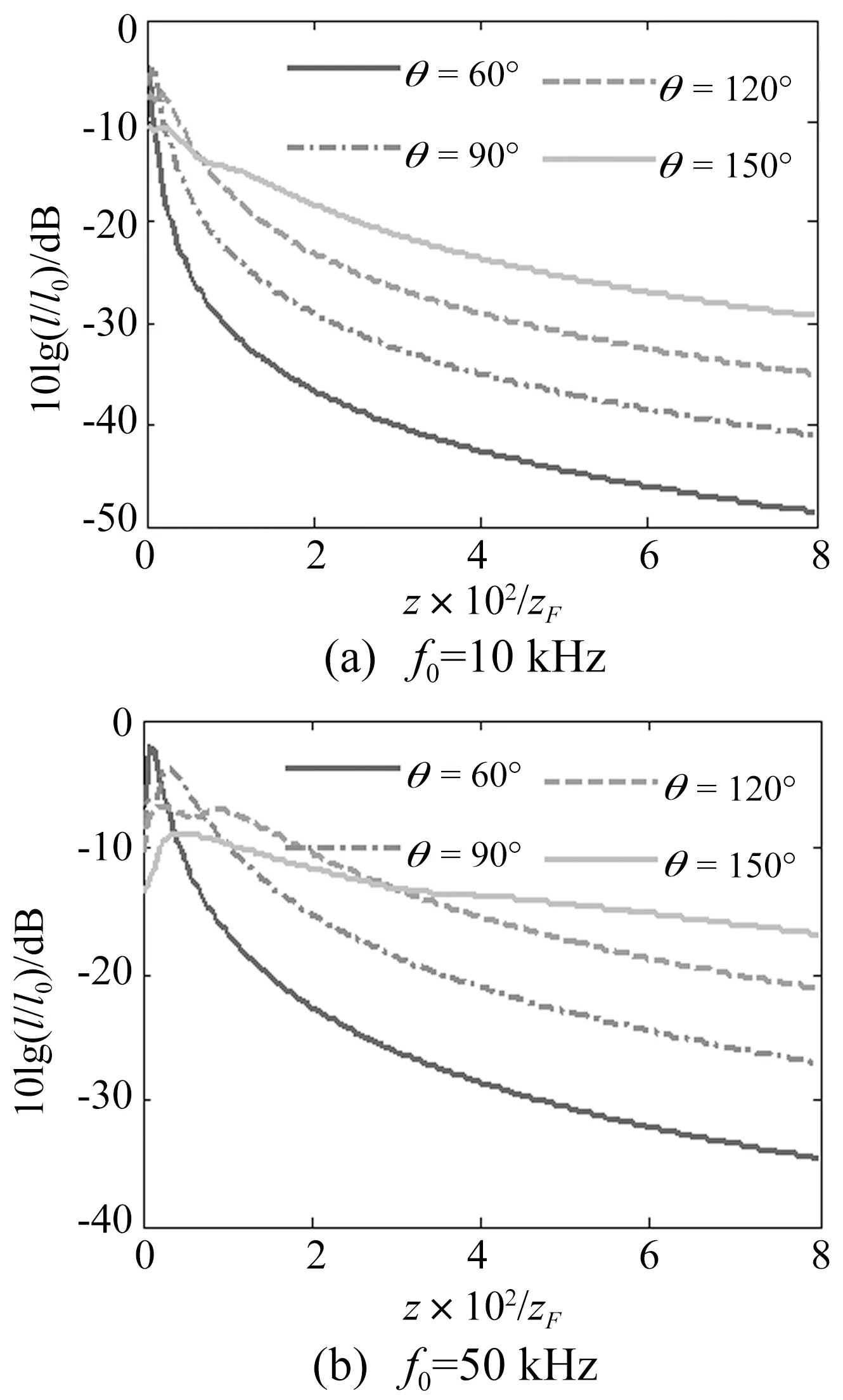
4 抛物面镜球面波反射声场的特性


5 结 论

