考虑热振特性的连续体结构拓扑优化设计

刘远东,莫　军,尹益辉,徐　兵

(中国工程物理研究院 总体工程研究所，四川 绵阳　621900)



考虑热振特性的连续体结构拓扑优化设计

刘远东,莫军,尹益辉,徐兵

(中国工程物理研究院 总体工程研究所，四川 绵阳621900)

为实现传热和振动条件下连续体结构的拓扑优化设计，以结构散热弱度最小化和动态特征值最大化加权函数为目标，建立传热和振动条件下连续体结构的多目标拓扑优化模型，实现了相应的算法和算例。方法中采用Rational Approximation of Material Properties(RAMP)方法对密度进行惩罚，利用优化准则法控制设计目标与材料分布，以敏度过滤技术抑制棋盘格效应，通过归一化目标函数有效地避免了不同性质目标函数的量级差异。通过算例，获得了热-振权重系数对结构拓扑构型和目标函数(宏观结构的散热弱度和基频)的影响规律，算例结果表明了该方法的有效性。

连续体结构；热-振多目标；拓扑优化；优化准则法

拓扑优化研究大多集中在单一物理场条件下的设计问题，如力场下的结构设计、温度场下的散热设计等。这些单一场下的结构优化研究对工程实际结构设计具有一定的指导意义[1-6]。然而，随着研究的深入和优化设计应用工程的要求，有必要开展更符合结构实际工作情况的多场条件下的优化设计研究。实际工程中，工作条件一般为力场、温度场、电磁场、流场等多场耦合。其中高温-振动复合问题就是一种典型的多场耦合问题，例如航空发动机、核电站、高速飞行器等。这类结构通常工作在高温-振动环境下，因此热应力和振动成为影响结构刚度、应力、频率和寿命的重要因素，有必要开展热-振作用下结构拓扑优化设计研究。热-振作用下结构的拓扑优化设计一般为：一方面需要热控制，具有足够的散热性或隔热性，以便使结构获得合适的温度；另一方面又需要振动控制，使结构远离工作频率，以避免共振现象。

目前，对于热激励结构拓扑优化设计，由于热载荷属于隐含力，依赖于材料的分布，导致热弹性耦合结构的拓扑优化求解存在很大困难，相关的研究工作很少。LI等[7]基于ESO方法，以有限元离散厚度为设计变量、材料用量为约束，开展了均匀稳态温度场下热、力耦合拓扑优化问题的研究。CHO等[8]则基于灵敏度分析方法研究了稳态温度场下热弹性弱耦合问题的结构拓扑优化设计。然而，上述文献中热力耦合拓扑优化结果存在严重的中间密度分布。左孔天等[9]以解耦的形式，建立了散热弱度最小和柔顺度最小的优化模型，开展了热力多目标拓扑优化设计研究。在以上工作基础上，张卫红等[10]讨论了基于最小柔顺度和弹性应变能为目标函数的两种热弹性拓扑优化设计方法，并给出了热、弹性载荷对优化结果的影响。ZHANG等[11-12]关于热振拓扑优化的工作是建立在均匀变化温度场下的，即在力场范围内通过线胀系数和温度差来表征热载荷，在某种程度上可以退化为振动拓扑优化，因此有必要开展考虑传热目标函数的更一般形式热-振拓扑优化研究。

本文针对轻质/隔热/减振结构的多目标拓扑优化问题，提出以散热弱度和动态特征值加权为综合目标的优化模型。针对不同性质的结构响应量在数量级上的差异，归一化处理各单一目标函数；采用优化准则法和敏度过滤技术控制设计目标和材料分布。比较不同热-振权系数下的多目标优化结果，揭示了不同权系数对目标函数的影响规律。结果表明同时考虑传热特性和振动特性的连续体结构多目标拓扑优化更有利于提高结构的综合性能。由于目标函数对密度灵敏度是建立在单元热能、应变能和动能的基础上，可以有效的移植到商业软件的二次程序开发中，有利于开展工程计算。同时算例结果表明该方法对于凸问题是有效性。

1　热-振多目标优化设计模型

1.1归一化多目标函数

对结构设计区域进行有限单元离散后，采用常见的RAMP方法，有限单元材料的热传导系数H、弹性模量E和质量M的插值计算式为：

(1)

(2)

(3)

式中:H0、E0和M0分别为实体材料的热传导系数、弹性模量和质量，xi∈[0,1]为单元材料的伪密度值，α为惩罚因子，对介于0和1之间的伪密度值进行惩罚，见文献[13]，本文后面取α=3。对结构设计区域进行有限单元离散后，采用敏度过滤技术[13]抑制有限元计算中的棋盘格现象。

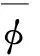
Findxi(i=1,2,…,n)

(k=1,2,…,ndy)

(4)

ConstraintⅠ:P=HT

ConstraintⅡ:(K-λkM)φk=0

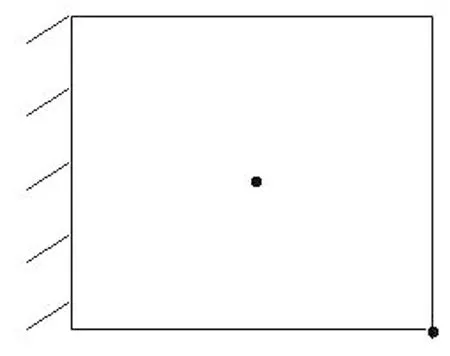
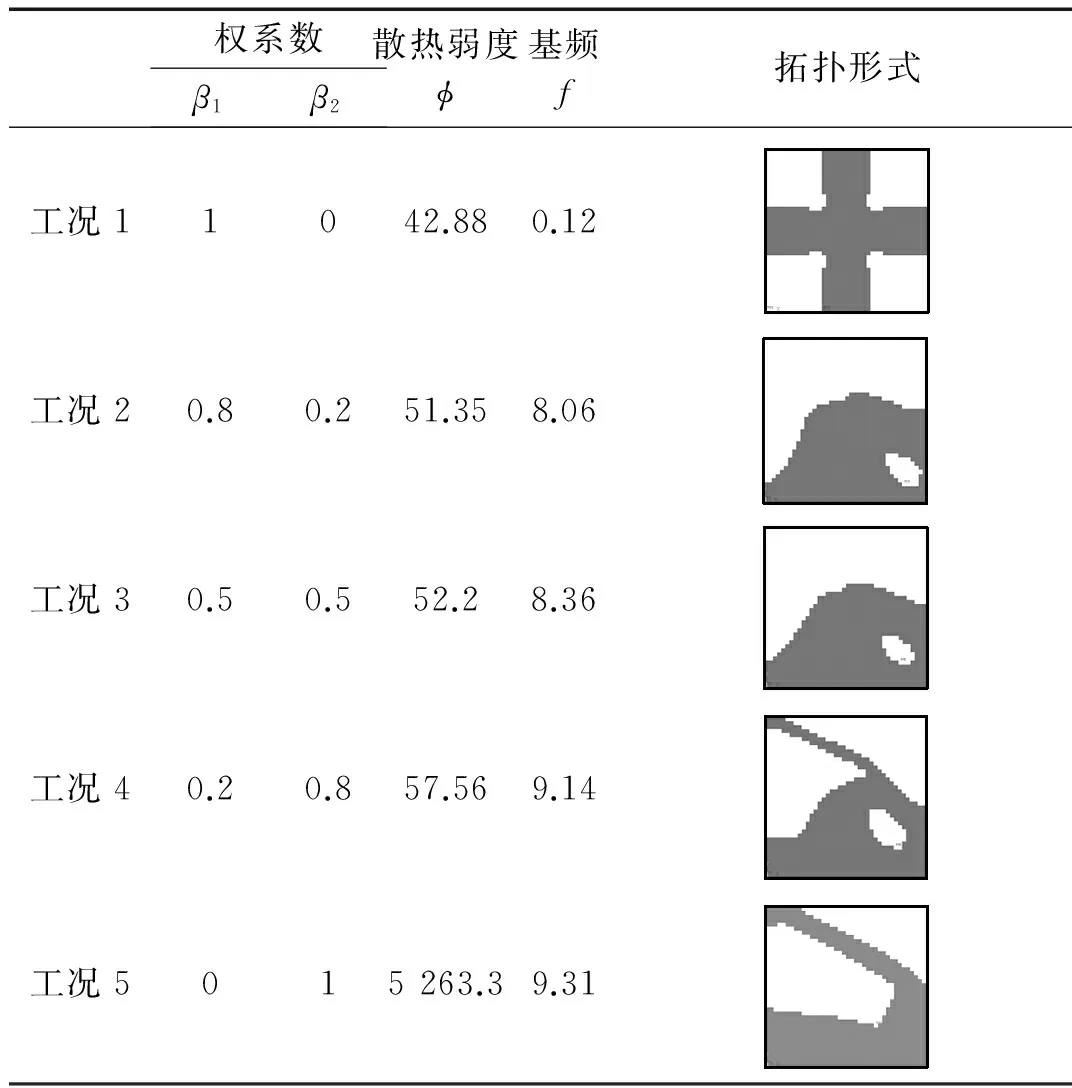
ConstraintⅣ:0

i=1,2,…,n

式中，βr是权重系数，φ表示结构的散热弱度，λk是结构第k阶圆频率的平方(特征方程的特征值)。约束Ⅰ是稳态热传导有限元平衡方程，P为热载荷列阵，H为热传导矩阵，T为节点温度列阵；约束Ⅱ是自由振动控制方程，φk是结构的第k阶特征向量，与λk形成特征对，M为结构的质量矩阵；约束Ⅲ给出了实体材料用量上限，vi为单元i的体积，V为给定的实体材料用量。约束Ⅳ是密度变量的上下限约束，xmin为趋于0的正数(取10-3)，以避免计算中出现刚度矩阵奇异,xmax是有限单元的最大密度值。式(4)同时考虑了结构的传热特性和振动特性，该拓扑优化设计方法有利于连续体结构有效性能的提高。

1.2灵敏度分析

热振作用下连续体拓扑优化设计的目标函数是一个综合考虑传热和振动特性联合优化的问题。在目标函数归一化后，对传热问题和振动问题的灵敏度求解分别如下：

对于热传导问题，结构总热能表示为

(5)

式中，Tene是热能，ti和hi分别表示与第i个单元对应的温度和单元热传导矩阵。

由式(5)求得散热弱度φ对伪密度xi的灵敏度为

(6)

式中:φ为结构的散热弱度。

对于动力问题，结构系统自然圆频率与相应模态向量的关系为

(7)

将质量矩阵正则化，可得圆频率对伪密度xi的灵敏度为

(8)

式中:Tenei、Dsenei和Dkenei分别表示单元i的热能、应变能和动能。由于目标函数(散热弱度+频率)对密度的灵敏度均建立在单元热能、应变能和动能的基础上，可以方便的移植到商业软件的二次程序开发中，因此式(4)的优化模型计算效率高，更适于求解工程优化问题。

1.3设计变量的迭代格式

基于变分原理的泛函形式，引入Lagrange乘子构造的Lagrange函数，将有约束的问题转化为无约束的极值问题，求解目标函数满足一系列约束条件的驻值问题，基于Karush-Kuhn-Tucker(KKT)条件，结合文献[15]，可得如下变量更新迭代格式：

(9)

式中：xi为设计变量，ξ为阻尼系数，文中取0.5，m为移动极限，可以在0与1之间变化，本文取0.3，λj为约束的拉氏算子，且有

(10)

2　优化步骤和方法

对热-振作用下连续体结构进行拓扑优化设计的流程图见图1，基本步骤如下：

1)初始化，宏观结构的传热学、动力学分析：划分有限单元网格、计算散热弱度和基频；

2)按式(6)和式(8)进行连续体结构热-振多目标优化的灵敏度分析；

3)按式(9)进行设计变量迭代，采用敏度过滤技术抑制棋盘格现象；

4)设计变量更新；

5)判断是否满足约束条件，如果不满足，则重复步骤2)～4)，如果满足，则进行后处理，输出相关参数。

图1　热-振作用下连续体结构多目标优化设计流程图Fig.1　The flowchart for thermal-vibrational multi-objective optimal design of continuum structure

3　数值算例

设计区域为一正方形板，如图2所示，其边长a=40，厚度t=5。基体材料的弹性模量E=2×105，泊松比ν=0.3，密度ρ=1×10-6，比热容C0=875，热导率K0=10。这里各物理量均为无量纲量。材料用量为初始结构的50%。有限元网格为40×40。板的中心点受热流率Q0=10的作用，板的右下角顶点受集中质量m=2的作用。传热学的边界条件为中心加热，四边温度为T=0℃；力学边界条件为左边固支。表1给出了5种不同热、振权系数条件下结构的优化设计结果。β1和β2分别表示热、振权重系数。

图2　设计区域Fig.2　Design domain

权系数β1β2散热弱度ϕ基频f拓扑形式工况11042.880.12工况20.80.251.358.06工况30.50.552.28.36工况40.20.857.569.14工况5015263.39.31

由表1可得，热传导单目标拓扑优化后，板的散热弱度φ=51.35，板的基频f=0.12；动态单目标拓扑优化后，散热弱度φ=5 263.3，板的基频f=9.31。热-振权系数β1=0.5、β2=0.5时，拓扑优化后，板的散热弱度φ=52.2，基频f=8.36。可以看出，拓扑优化后，结构的热、振目标函数分别随着热、振权系数的增加而变得更好，随着热、振权系数的减少而变得较差。同时可以看出单目标优化的单项结果优于多目标优化对应的结果，但结构优化是在各种可能的结构形式中取得最佳“折衷”的设计过程，因此热-振多目标拓扑优化同时考虑传热和振动特性，更能体现结构综合性能的提高。

4　结　论

本文建立了热-振多目标优化设计模型，实现了相应的算法和算例。通过算例，验证了方法的有效性，得到了热-振权重系数对目标函数和结构构型的影响规律。根据结果，单目标优化的单项结果优于多目标优化对应的结果，但多目标优化更好地满足连续体结构在使用中需要的综合性能。同时将目标函数的灵敏度均建立在单元热能、应变能和动能的基础上，使计算效率更高，可以方便地移植到商业软件的二次程序开发中，更适合于工程优化问题。

[1]周克民,李俊峰,李霞.结构拓扑优化研究方法综述[J].力学进展，2005,35(1):69-76.

ZHOU Kemin,LI Junfeng,LI Xia.A review on topology optimization of structures [J].Advances in Mechanics,2005,35(1):69-76.

[2]罗震,陈立平,黄玉盈，等.连续体结构拓扑优化设计[J].力学进展,2004,34(4):463-476.

LUO Zhen,CHEN Liping,HUANG Yuying.Topological optimizationdesign for continuum structures [J].Advances in Mechanics,2004,34(4):463-476.

[3]MATHIEU-POTVIN F,GOSSELIN L.Optimal conduction pathways for a heat generating body:a comparison exercise [J].International Journal of Heat Mass Transfer,2007,50(5-16):2996-3006.

[4]LI Q,STEVEN G P,XIE Y M,et al.Evolutionary topology optimization for temperature reduction of heat conducting fields [J].International Journal of Heat and Mass Transfer,2004,47(23):5071-5083.

[5]GERSBORG-HANSEN A,BENDSOE M P,SIGMUND O.Topology optimization of heat conduction problems using the finite volume method [J].Structural and Multidisciplinary Optimization,2006,31(4):251-259.

[6]ZHANG Y,LIU S.Design of conducting paths based on topology optimization [J].Heat and Mass Transfer,2008,44(10):1217-1227.

[7]LI Q,STEVEN G P,XIE Y M.Displacement minimization of thermo-elastic structures by evolutionary thickness design [J].Computer Methods in Applied Mechanics Engineering,1999,179(3/4):361-378.

[8]CHO S,CHOI J Y.Efficient topology optimization of thermo elasticity problems using coupled field adjoint sensitivity analysis method [J].Finite Elements in Analysis and Design,2005,41(51):1481-1495.

[9]左孔天,赵雨东,陈立平.传热结构的多目标拓扑优化设计研究[J].计算力学学报,2007,24(5):620-627.

ZUO Kongtian,ZHAO Yudong,CHEN Liping.Study on multiple objective topology optimization of thermal conductive structure [J].Chines Journal of Computational Mechanics,2007,24(5):620-627.

[10]ZHANG W H,YANG J G,XU X J,et al.Topology optimization of thermoelastic structures:mean compliance minimization or elastic strain energy minimization [J].Structural and Multidisciplinary Optimization,2014,49(3):417-429.

[11]YANG X W,LI Y M.Topology optimization to minimize the dynamic compliance of a bi-material plate in a thermal environment [J].Structural and Multidisciplinary Optimization,2013,47(3):399-408.

[12]YANG X W,LI Y M.Structural topology optimization on dynamic compliance at resonance frequency in thermal environments [J].Structural and Multidisciplinary Optimization,2014,49(1):81-91.

[13]SIGMUND O.Morphology-based black and white filters for topology optimization[J].Struct Multidisc Optim,2007,33 (4/5):401-424.

[14]刘远东.材料/结构一体化静动力学多目标优化设计和两尺度实验研究[D].绵阳:中国工程物理研究院总体工程研究所,2007.

[15]BENDSOE M P,SIGMUND O.Topology optimization theory,methods and application[J].Berlin:Springer,2003:71-75.

Topologic optimization design for a continuum structure considerating its thermal and vibrational performances

LIU Yuandong,MO Jun,YIN Yihui,XU Bing

(Institute of Structural Mechanics,CAEP,P.O.Box 919-401,Mianyang 621900,China)

For thermal and vibrational design problems,taking the minimum dissipation of heat transport potential capacity and the maximum fundamental frequency as objectives,a thermal and vibrational collaborative optimization model for a continuum structure was developed and corresponding numerical simulations were conducted.In the model,the rational approximation of material properties (RAMP)method was adopted to ensure clear topologies,the design objectives and material distribution were controlled with the optimization criteria method and the checkerboard effect was eliminated with the sensitivity filtering technique.To improve the smoothness of objective functions and avoid the singularity of numerical computation,the weighted objective functions were normalized.Based on numerical simulations,the effects of weight coefficients of thermal and vibrational optimization on the topologic configuration and objectives (the dissipation of heat transport potential capacity and fundamental frequency)were investigated and the results indicated that the proposed method is effective.

continuum structure; thermal-vibrational multiple-objective; topologic optimization；optimization criteria method

国家自然基金重点项目(11432011)；中国工程物理研究院重点学科项目“计算固体力学”资助

2015-04-07修改稿收到日期：2015-07-27

刘远东 男，副研究员，博士，1978年生

尹益辉 男，研究员，博士，1965年生

TB303

A DOI:10.13465/j.cnki.jvs.2016.17.019