零中频接收机中的载波粗估计

魏苗苗，王竹刚，，安军社

（1.中国科学院大学北京100190；2.中国科学院空间科学与应用研究中心北京100190）

零中频接收机中的载波粗估计

魏苗苗1，王竹刚1，2，安军社2

（1.中国科学院大学北京100190；2.中国科学院空间科学与应用研究中心北京100190）

针对零中频接收机的卫星通信应用，文中首次将频域移位平均周期图法应用于零中频接收机，利用该算法工作信噪比低、估计范围大的优点，扩展了零中频接收机的载波捕获范围，并对算法中补零倍数的定义进行了修改。仿真结果表明，在信噪比大于2 dB，经典高动态模型的通信环境中该算法可使接收机达到90%捕获概率，且捕获时间不大于1.2s。

信号处理；零中频；大频偏；频域移位平均周期图法；FFT

零中频接收机（Zero-IF Receiver）［1-2］是目前实现接收机集成化的重要技术手段，最早出现在二十世纪初，随着微电子技术的进步才得以实现。零中频技术最大的优点是将解调中频信号完全转化为了基带信号，即完全剥离了已知的载波成分，从而可以省去片外滤波过程，极大地降低了后级信号处理的复杂度，简化了硬件结构。而且由于系统结构的简化，电路模块和外部节点数都相应减少，使得接收机所需的功耗减少，同时降低了外部干扰对射频信号的影响。因此，基于零中频结构的集成化芯片接收机不断涌现。但是由于收发前段噪声较大，致使接收机灵敏度较低的问题随着零中频技术在卫星通信系统中的应用不断推广变得愈加突出［3］。

基于FFT的载波粗估计算法是现有信号捕获算法的主流算法［4-9］，其中平均周期图法［7-9］针对低信噪比高动态应用可在信噪比为2 dB时实现多普勒频偏估计范围达百kHz，多普勒变化率估计范围达近千Hz/s。文献［7］提出的多支路时域匹配傅里叶变换，采用并行方式提高算法计算速度，捕获时间极大缩短，估计精度得到提高，但是算法要求匹配精度高，匹配支路数目随着动态范围的增加而增加，FFT点数巨大，对存储资源和计算速度要求较高。文献［9］提出了带有补零的频域移位平均周期图法，不仅减少了运算复杂度，而且提高了估计精度。因此，本文选择带有补零的频域移位平均周期图法实现零中频接收机中的信号捕获过程。

1　信号模型

接收到射频信号经AD采样后，首先与接收机本振产生的正余弦混频完成载波剥离，得到中频信号。接收机与发射机之间存在相对运动，使得中频信号中产生了多普勒频偏变化量。由于相对运动的不规律性，实际中系统的多普勒频偏多是呈非线性变化。但是为了便于分析，均衡载波粗估计算法的复杂度、估计精度以及动态范围大小，采用线性模型对中频信号进行频偏估计可以满足通信系统要求。因此中频信号的频偏可表示为［10］：

零中频接收机的中频信号可表示为：

式中：A为信号幅度；fd为多普勒频偏；a为多普勒变化率；θk为MPSK调制相位；n（t）为零均值、方差为σ2的高斯白噪声。

2　零中频接收机结构

如图1所示，零中频数字接收机首先将射频输出信号与载波频率相同的本振信号相乘，输出I、Q两路混频信号，经过低通滤波器之后再进行模数变换和零中频解调。由于在零中频结构中是对基带信号进行滤波和采样，可以采用易于实现的低通滤波器以及采样率低的模数转换器。虽然零中频结构存在着直流偏差、本振泄漏，但是一般会在电路中设置调节电路和抵消措施以克服此类问题。

图1　零中频数字接收机结构［1］

基带处理是零中频接收的核心，而量化后信号的处理首先是载波参数的估计问题。随着零中频接收机在卫星通信中的推广应用，针对卫星通信中低信噪比高动态的应用环境，文中选择采用频域移位平均周期图法完成零中频接收机的载波捕获过程。

3　频域移位平均周期图法

3.1算法原理

频域移位平均周期图法是根据傅里叶变换的频移性质，将时域平均周期图法进行的频率匹配操作通过傅里叶变换后的频域移位完成。然后比较选择频谱最大值，以最大值所在支路对应的多普勒变化率和频偏作为估计结果。

但由于频率分辨率不够，使得该算法进行移位时，会遇到移位步进值远小于1的情况，造成支路移位结果相同的情况。但是若通过增加采样数据长度来提高信号频谱图频域分辨率，会增加算法捕获时间。因此文献［9］提出的带有补零的频域移位周期图法，在有效数据长度不变的情况下补零采用数据段后补零的方式，增加FFT运算长度，实现了有效地频域移位，使FFT的频率分辨率得到了提高。

接收信号频域表示为：

由式（4）可知，不同支路接收信号的频域表达式等价于对函数S（f）做不同速率的频域移位。根据傅里叶变换性质，同一时刻数据段时域不同变化率补偿等价于将数据段做傅里叶变换后以不同速率aT（或△arT）沿横轴进行频域移位。因此，为了实现信号频谱峰值的累积、减少FFT计算次数，各个支路的频谱图可通过该段数据的FFT结果在各个支路以不同速率逆向移位实现。该算法的原理图如图2所示［9］。

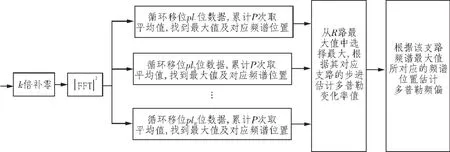
图2　频域移位平均周期图法框图

图2中：p=1，2，…，p为累计次数。设分配给各支路的匹配多普勒变化率a1，a2，…，aR，其中支路数为R。设系统采样率为fs，单次取样点数为N，则各支路单次循环移位数lr表达式为：

经过移位和累加后，接收信号平均周期图功率谱表示为

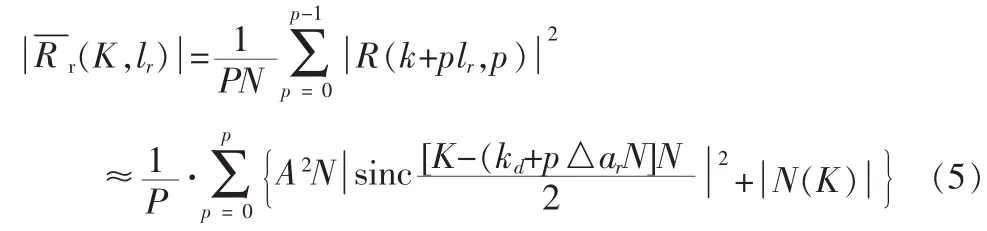
由式（6）可知，经逆向移位后各支路功率谱中sinc函数包含的残余多普勒变化率为△arT，支路的残差速率△arT越小说明所在支路的多普勒变化率估计值与真实值越接近，残差速率△arT最小的支路的信号频谱经多次累加后，在真实频率附近不断累积，得到最大值，该值所对应频率和该值所在支路对应的频移速率即为载波多普勒频偏及变化率估计值。

3.2参数设计

设信号多普勒频偏估计范围为［fdmin，fdmax］，多普勒变化率估计范围为［amin，amax］，后级载波细估计部分可估计范围：多普勒频偏±fpre、多普勒变化率±apre。参数设计［9］步骤如下：

1）astep和ar：兼顾精度和复杂度要求选取astep=2apre，根据［amin，amax］，确定：

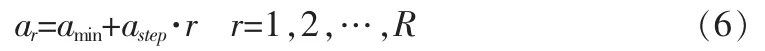
R为总匹配支路数。

2）采样率fs：由线性调频信号频谱分布可知，采样率决定了信号频率的变化范围，因此为频偏变化范围内信号均能被正确采集，需满足fs≥2（fdmax-fdmin），为了给频偏变化率留有余量，选择fs=3（fdmax-fdmin）。

3）根据功率谱峰值位置与采样点数的关系，为取得功率谱最大值选择采样点数：

4）累加次数P：P值的增加可以提高捕获概率，增加信号功率谱峰值，减少噪声功率谱方差，但是过多的累加次数会造成系统计算负担，也会增加算法捕获时间。在信噪比极低情况下，需保证P次累加中信号频率跨过一个频率分辨率区间，即。因此可得P≥/（N2astep）。

5）补零倍数k：补零是为了增加多普勒频偏估计的频率分辨率，为使单次移位最小的匹配支路的每次可移位半个频率分辨率，k值选取应满足：

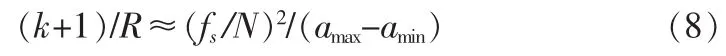
此外，在增加支路数的同时，需要同时增加补零倍数，才能有效区分取整后的各支路移位数。

4　仿真及复杂度分析

设信噪比Eb/N0在0～10 dB内变化，基带码速率Rb=20 bps，采样率fs=800kHz，采用美国JPL实验室提出的高动态接收信号模型［7］，多普勒频偏fd∈（-300，300）kHz，变化率a∈（-800，800）Hz/s。后级载波跟踪要求载波粗捕获精度需达到fpre≤30 Hz，apre≤25 Hz/s，捕获时间小于1.2s。

根据3.1完成算法参数设计：N=32 768，其他参数设置见图3。在设定范围内随机产生信号频偏和变化率，分别统计在累加次数和信噪比不同的情况下算法可达误捕概率，观察算法的性能。

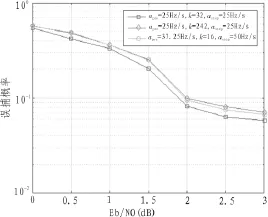
图3　不同补零倍数、不同信噪比频域移位平均周期图法的误捕概率

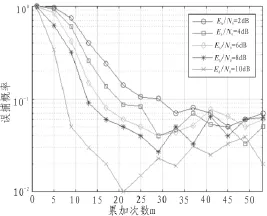
图4　不同累积次数、不同信噪比情况下频域移位平均周期图法误捕概率

如图3，apre=25 Hz/s，k=31和apre=37.25 Hz/s，k=15时两条曲线几乎重合，可知，验证了对补零倍数计算公式的修改。而3种设置均可以在Eb/N0=2 db时使捕获概率大于90%。为减少计算复杂度，选择补零倍数k为15，后级跟踪精度apre为37.25 Hz/s。

通过仿真，当信噪比在2 dB以上时实现90%误捕概率最高需要29次累加，耗时N·m/Rb=32 768×29/800 000≈1.19s。而且随着信噪比的提高，误捕概率不断减小，达到90%捕获概率所需的累加次数减少，捕获时间随之减少。

5　结论

经过仿真，验证了对补零倍数的分析，纠正了补零倍数的定义，并确定了不同信噪比条件下累积算法所需的累积次数。算法采用多支路估计扩展了载波捕获范围，通过多次累积降低了算法工作的信噪比范围，通过频域移位减少了计算复杂度。该算法可以实现在不同信噪比时高动态频偏范围的有效估计，捕获时间短，应用范围广。

［1］强刚，刘乃安，刘增基.高速突发通信零中频接收技术［J］.西安电子科技大学学报，2002，29（2）:192-195.

［2］陈伟，郑肇健.卫星移动通信终端的零中频射频接收机设计［J］.电讯快报，2014（6）:31-34.

［3］常高嘉，零中频接收机的研究和硬件设计［D］.成都：西南交通大学，2013.

［4］Nawrocki C W.ZOOM FFT-An Approximate Vemier Frequency Algorithm［R］.TM-SA2201-584-72.NUSC.22 Nov.1972.

［5］SHAN Tao，TAO Ran，SUN Rong-rong.A fast method for time delay，Doppler shift and Doppler rate estimation［C］∥CIE'06 International Conference on Radar，2006:1-4.

［6］Pan X.ALE-FFT algorithms for weak signal acquisition［C］∥IEEEInternationalSymposiumonIntelligentSignal Processing and Communication Systems（ISPACS 2010），2010:1-4.

［7］韩孟飞，王永庆，吴嗣亮，等.一种低信噪比下LFM信号参数快速估计算法［J］.北京理工大学学报，2009，29（2）:147-151.

［8］Satorius E，Estabrook P，Wilson J，etal.Direct-to-Earth communications and signal processing for Mars exploration rover entry，descent and landing［R］.IPN Progress Report 42-153，2003:1-5.

［9］段瑞枫，刘荣科.一种低复杂度的极低信噪比高动态信号载波粗捕获算法［J］.航空学报，2013，34（3）:662-669.

［10］韩孟飞，崔嵬.极低载噪比高动态信号的捕获策略研究与仿真［J］.系统仿真学报，2009，21（23）:7589-7592.

The coarse carrier estimation in Zero-IF receiver

WEI Miao-miao1，WANG Zhu-gang1，2，AN Jun-she2
（1.University of Chinese Academy of Science，Beijing 100190，China；2.Beijing National Space Science Center，Chinese Academy of Science，Beijing 100190，China）

Focusing on extending the application of Zero-IF receivers on satellite communication，the average periodogram algorithm in frequency domain is used in carrier acquisition process of Zero-IF receivers to extend the acquisition scope.And some parameters of the algorithm are corrected in this paper.The simulation denotes:the algorithm can make sure the Zero-IF receiver's acquisition ratio reach 90%when SNR＞2 dB and Doppler frequency bias and derivate satisfies the classical dynamic model，and the carrier acquisition time is less than 1.2s.

signal processing；Zero-IF；large frequency bias；average periodogram algorithm in frequency domain；FFT

TN927+.21

A

1674－6236（2016）17-0090-03

2015-09-04稿件编号：201509023

魏苗苗（1987—），女，河南鹿邑人，博士研究生。研究方向：信号与信息处理、测控通信。