基于矩阵分解与用户社会关系的协同过滤推荐算法
朱爱云
(潍坊科技学院计算机软件学院,寿光2627002)
基于矩阵分解与用户社会关系的协同过滤推荐算法
朱爱云
(潍坊科技学院计算机软件学院,寿光2627002)
矩阵分解技术虽然已成功应用到协同过滤推荐系统中,但是基于矩阵分解的传统协同过滤方法仍然存在着数据稀疏性、冷启动等问题。为了进一步提高系统推荐的准确性,提出将用户间的社交关系融合到矩阵分解的协同过滤推荐系统中,该方法以奇异值矩阵分解推荐模型为核心,对该模型添加用户偏置和项目偏置,同时将用户在社交网络中的朋友关系添加到矩阵分解模型中,然后采用一种随机梯度下降法对该矩阵进行分解,得到用户潜在特征和物品潜在特征。最后通过实验结果验证表明,所提出的算法具有较好的预测效果,其性能明显优于现有的相关算法。
协同过滤;矩阵分解;推荐系统;梯度下降
0 引言
面对网络的爆炸式增长,人们会变得迷失在网络的信息海洋中,用户为了搜索有用的个性化信息,经常花费很多的时间。面对这样一个问题,许多研究人员从不同领域发明了各种工具,其中,搜索引擎是最突出的。但是与推荐系统相比,搜索引擎在根据用户历史的行为为用户自动匹配口味时不够个性化,为了满足用户更个性化的需求,推荐系统由此产生。随着互联网的全面普及和电子商务的逐步完善,推荐系统已经成为了一个越来越受到关注的研究领域。在各种各样的推荐系统中,协同过滤方法是学术界和工业界最为关注的一种方法,由于其不需要具有领域知识,容易实现和检测复杂模式的优点。特别是,在Netflix奖的竞赛中激发了不同领域的研究者提出不同的解决方案,建立了相应的推荐系统。协同过滤的基本思想是根据目标用户的邻居兴趣爱好来预测目标用户的兴趣爱好。邻居是一组对相同物品具有相似口味的人,其中,协同过滤有两种主要类型:基于邻居方法和基于模型方法,在早期,基于邻居方法包括基于用户和基于项目方法,这两种方法是最广泛应用于工业界,如亚马逊和谷歌。目前,学术界和工业界的专家已经见证了基于模型方法的良好性能,基于模型的方法是根据已知的用户评分矩阵建立一个模型,并应用该模型对要评价的项进行评分。许多基于模型的协同过滤方法已得到广泛研究,主要包括潜在特征模型、聚类模型[5]、贝叶斯网络模型等。其中,基于潜在特征的矩阵分解模型[6,8,12-13],由于能在训练过程中分别为用户和物品推导出与其对应的低维潜在特征向量,以及在大数据集上所具有的高可扩展性和准确性,因此受到了研究者们的广泛关注。
然而,传统的协同过滤算法也有自身的缺点(1)在实际的推荐系统中用户项目评分矩阵往往极其稀疏,因此缺少足够的评分或购买历史信息使得很难找到相似的用户。(2)传统的推荐系统都认为用户是独立且恒等分布,没有考虑用户间的社会关系,但是在我们的日常生活中我们通常会借助于朋友为我们推荐他们喜欢的物品,我们与自己最亲密的朋友往往有许多相同的兴趣,同时我们的兴趣爱好无形之中也会被周围的朋友所影响。因此,在推荐系统中增加社会关系会提高推荐质量[1,8-9]。近年来,由于矩阵分解方法具有良好的扩展性和预测准确度,因此受到越来越多的关注。在本文中为了进一步提高推荐质量,在前人[12-13]研究的基础上,我们提出在目标函数中增加用户、物品偏置信息的基础上,将用户的社会关系融合到奇异值矩阵分解的推荐模型中。通过相关实验验证了融合用户的社会关系对协同过滤推荐方法能起到一定的优化作用,并且也能应用于现实生活中的大规模数据集中。
2 问题定义
近年来矩阵分解[10-11]是最流行的协同过滤方法之一,它假设一个用户的偏好可以用少量的未被注意的特性所表示,将用户-项目评分矩阵R∈Rm×n分解成两个低维用户特征矩阵p∈Rm×k和项目特征矩阵q∈Rn×k,其中,m,n分别表示为用户数和项目数,k为潜在特征数,且k≤min(m,n)。一般用户仅对一小部分项目进行评分,因此R矩阵是非常稀疏的。
假定ru,i是用户u对物品的评分,,表示用户u对物品i的预测评分,其中预测评分,是由用户特征向量pu和项目特征向量qi的内积计算得到。公式如下:

最关键的问题就是如何利用已有的评分训练用户潜在特征矩阵p和物品潜在特征矩阵q。
方法如下:
首先,对矩阵p和q进行随机初始化。
其次,对训练集中所有的用户-物品指示对(u,i),计算模型的预测误差。
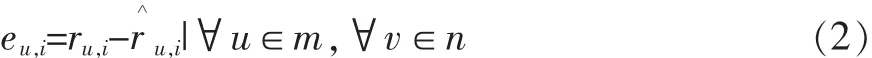
最后,通过最小化全局误差的平方和,来获取模型参数即矩阵p和q。
公式如下:

由于评分矩阵过于稀疏,为了防止学习过拟合,所以在目标函数中加入惩罚因子λ(||qi||2+||pu||2)来约束模型参数的取值,目标函数修改为:
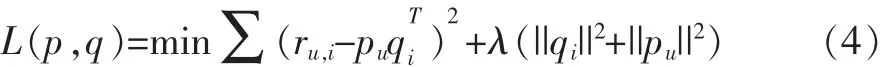
然而,在实际的推荐系统中,一些用户往往比别的用户打分高,一些项目也往往给予很高的评分,因此在文献[12,13]中提出了预测评分为:

其中,bu为用户的偏置评分,bi为项目i的偏置评分,e为数据集中所有评分的平均评分。
虽然这些传统的协同过滤算法在学术界和工业界都已经取得了较好的研究成果,但是数据稀疏性和冷启动问题是推荐系统最主要的挑战。近几年,为了处理这些问题许多研究人员已经提出了一些将社会关系融合到矩阵分解的推荐方法,大大提高了推荐的准确度,文献[2,7,8,9,14]提出了社交网络下的信任感知推荐系统,Ma等人[1]提出了在目标函数中增加社会正则化条件,来衡量一个用户和他朋友的潜在特征向量之间的差异,通过梯度下降算法使目标函数达到局部最小化。Li等人[3]提出了将关系正则化矩阵分解添加拉普拉斯算子的正则化社会关系到目标函数中并且通过选择投影算法使目标函数最小化。Jamali等[4]提出了一种基于概率图模型的矩阵分解方法,这种方法研究了基于信任传播的推荐算法,通过使用信任关系矩阵对目标函数进行约束,在学习过程中使目标用户的特征向量尽可能与其所信任朋友的特征向量接近,从而达到利用社会关系进行推荐的目的。
2 社会推荐方法描述
虽然增加偏置后的SVD比最初的SVD在推荐质量上有较大的提高,但是它仍然忽视了用户间的社会关系。在现实生活中为了能够产生更好的推荐,社会关系是一个强有力的工具,例如:如果一个人对购买一个物品不确定时,他通常咨询朋友或熟人并听取他们的意见,因为他们相信朋友的品味,有时为了做一个决定我们也会咨询许多朋友并听取他们的建议。因此我们在方法[12-13]基础上增加了用户的社会关系,目标函数修改为如下:
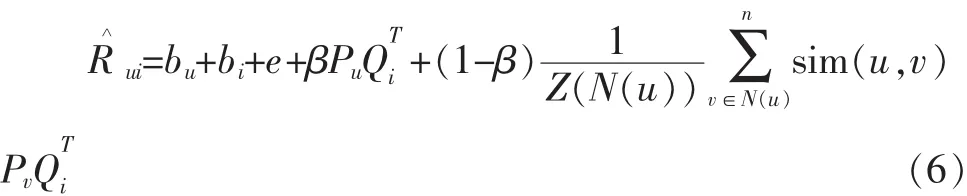
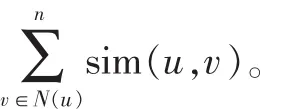
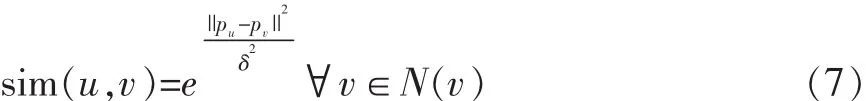
其中,pu,pv分别为用户u和v朋友的特征向量,δ是一个常量,在我们的实验中设定为0.1。因此目标函数改为:

其中λ1,λ2,λ3,λ4>0的常数用于调整过拟合。我们应用梯度下降法来解决最优化问题,因此需要首先对目标函数中的参数pu,qf,bu,bi分别求偏导,得到如下公式:
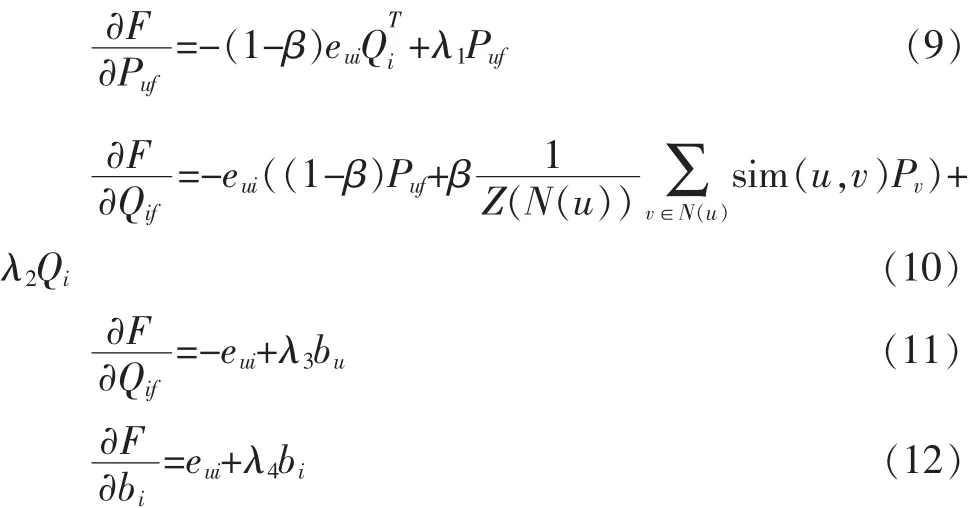
根据随机梯度下降法,得递推公式:
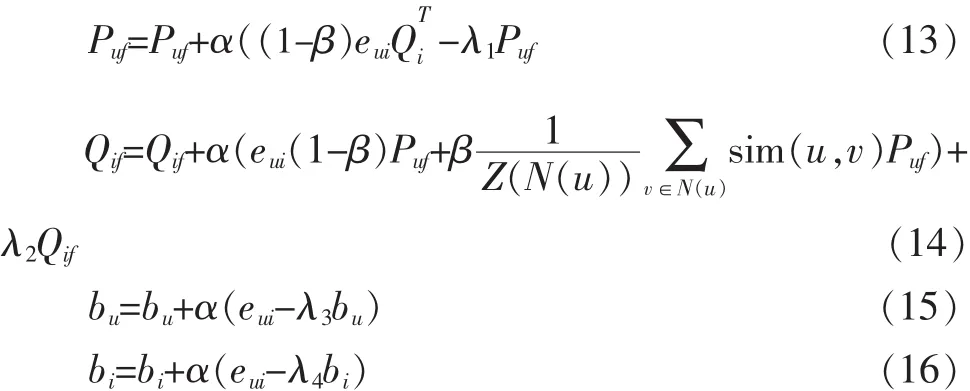
其中α是一个常数决定了迭代更新Puf,Qif,bu,bf后获取到最小预测误差的学习速率。eui表示真实评分与预测评分之差,公式如下:

3 实验结果及分析
3.1评价指标
我们使用两种指标分别是均方根误差(Root Mean Square Erorr,RMSE)和平均绝对误差(Mean Absolute error,MAE)来衡量我们提出方法的预测质量。
RMSE,MAE定义如下:
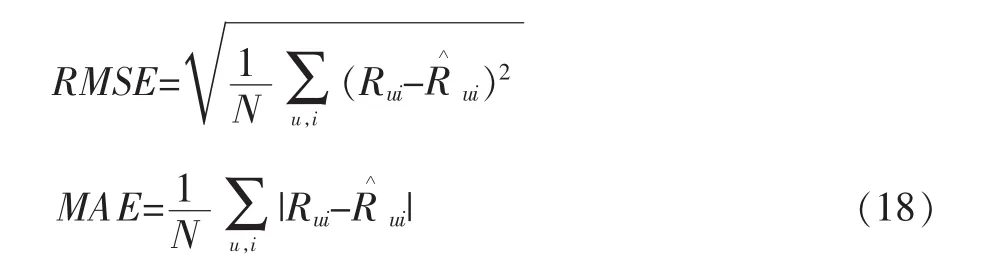
其中,Rui表示用户u对物品i的真实评分,表示用户u对物品i的预测评分,N为测试集中总的评分记录。显然,MAE或RMSE值越低,表示算法的推荐性能越好。
3.2数据集和实验结果
本实验采用的数据集为Flixster(www.cs.sfu.ca/~sja25/personal/datasets/),此数据集包含了用户对项目的评分和用户的社会关系,其中社会关系是对称的,Flixster是一个社会电影网站,允许用户分享电影评分,发现新的电影和满足其他具有类似电影的味道。用户数为147612个,电影数为48794部,评分记录数为29718794条,社交网络关系数据中朋友数为520543个。
在实验中,随机抽取了5000个用户的评分数据作为样本数据,并从样本数据中抽取80%作为训练集,剩余20%作为测试集,并且从社交网络关系数据中抽取10000个朋友作为训练集,学习速率参数α与正则化参数λ通过交叉验证决定。本文采用α=0.0002,λ1= 0.003,λ2=0.002,λ3=0.004,λ4=0.0005,β=0.2进行试验。在训练集中迭代次数选用10次。学习速率参数α按每次迭代缩减为0.9倍的速度递减,并令分解后的矩阵的特征维数分别为K=10,K=20,为了说明我们提出的算法的有效性,对比了以下算法在这两种情况下的预测准确度。
①SVD:这种方法已广泛应用于协同过滤推荐系统中,但它忽视了用户间的社会关系。
②Bias_SVD:这种方法是Koren在文献[16]中提出,它也仅仅使用用户项目评分矩阵来做推荐。
③Social_SVD:这种方法是在文献[12]中提出,它是一种信任感知推荐方法,用来平衡用户和他/她所信任朋友的偏好。
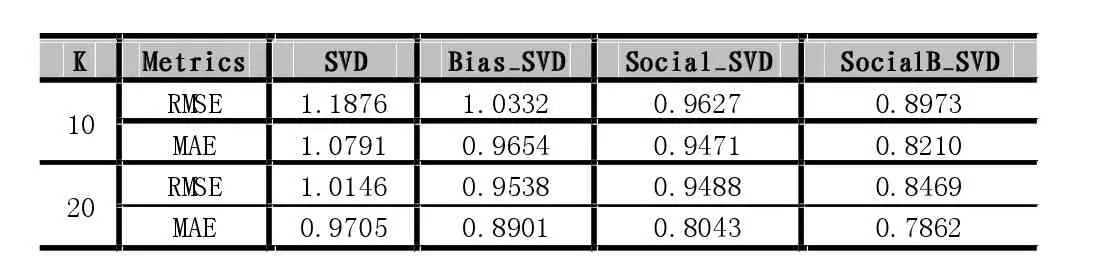
表1 本文方法与其他典型方法的准确度比较
从表1可以看出,我们提出的方法(SocialB_SVD)的MAE以及RMSE值均小于其他典型方法,表明融合用户的朋友信息可提高协同过滤的推荐准确度。
(1)特征维数K的影响
在本实验中分别选取K=10,20,30,40,50,60,100进行模型训练所得RMAE值如图1所示。从图1中可以看出,特征维数K对预测准确度影响较大,K值越大,实验精度越高。并且随着K值的增加,RMAE开始下降很快,但随着K值的逐渐增加RMAE下降速度明显变缓。

图1 特征维数K的影响
(2)社交网络信息权重参数β的影响
在本文中我们设置了一个参数β用来平衡用户自己的偏好和社交网络中的朋友偏好信息对推荐的影响力,如果我们取极端值,当β=0时,我们提出的方法(SocialB_SVD)只考虑社会关系中朋友的偏好信息,当β=1时,我们提出的方法(SocialB_SVD)仅仅考虑用户自己的偏好信息。为了获得β的最佳设置范围,在本实验中设定β∈[0,1],并以0作为初始值,以0.1作为步进值,分别取β=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9, 1.0进行模型训练。通过计算不同β值下的MAE与RMSE值得到图2、图3。从图2、图3可以看出随着β值的增加MAE或RMSE值减少,但当β值增加到β= 0.3时MAE,RMSE值达到最小值。当β值继续增加时,MAE、RMSE值均增加。通过实验验证我们只考虑个人的偏好信息或朋友的偏好信息都不能使推荐准确度达到最佳值即(MAE或RMSE)最小。只有既考虑用户自己的偏好,又要适当地考虑朋友的偏好才能取得最佳值。
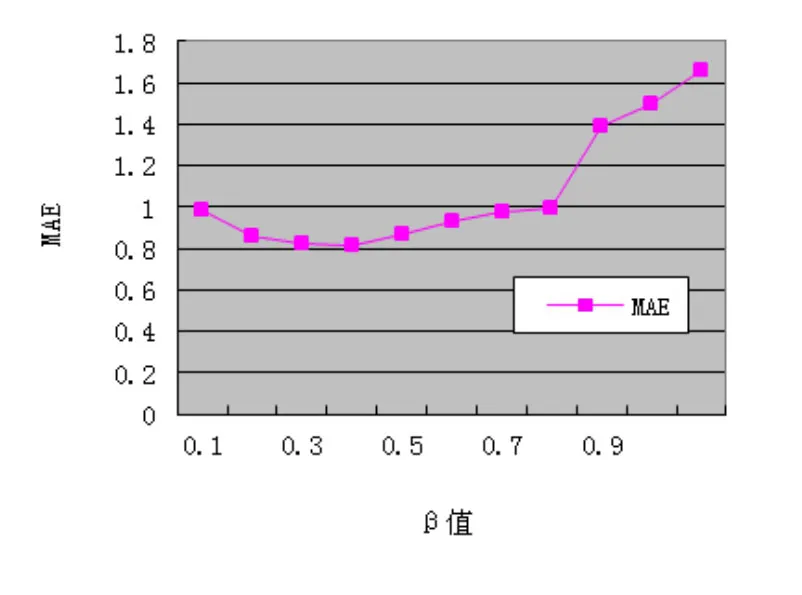
图2 不同β值下的MAE对比(K=10)
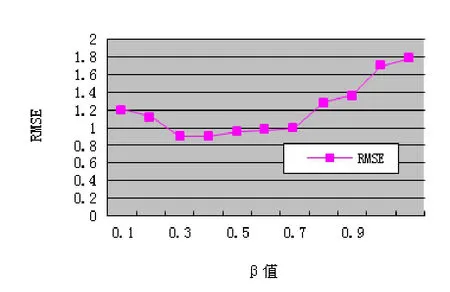
图3 不同β值下的RMSE对比(K=10)
4 结语
通过融合目标用户的朋友关系对矩阵分解推荐算法进行改进,实验结果表明,本文采用的是基于数据集Flixster中的朋友关系信息,虽然算法的精度得到了提高,但用户兴趣不仅与自己有关,还受信任朋友和评分项目的影响,因此在此基础上融合项目的隐式关系成为进一步提高推荐系统性能的一个研究方向。
[1]H.Ma,D.Y.Zhou,C.Liu,M.R.Lyu,I.King.Recommender Systems with Social Regularization,in:Proceedings of the 4th ACM International Conference on Web Search and Data Mining,2011,287-296.
[2]J.T.Liu,C.H.Wu,W.Y.Liu.Bayesian Probabilistic Matrix Factorization with Social Relations and Item Contents for recommendation,De-cision Support Systems,2013,6(55):838-850.
[3]W.J.Li,D.Y.Yeung.Relation Regularized Matrix Factorization,in:Proceedings of the 21st International Joint Conference on Artificial Intelligence,2009,1126-1131.
[4]M.Jamali,M.Ester.A Transitivity Aware Matrix Factorization Model for Recommendation in Social Networks,Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence,2011,2644-2649.
[5]F.M.Hsu,Y.T.Lin,T.K.Ho.Design and Implementation of an Intelligent Recommendation System for Tourist Attractions The Integration of EBM model,Bayesian network and Google maps[J].Expend Systems with Applications,2012,2(39):3257-3264.
[6]X.Qi,W.Wu,Y.Huang,T.L.Huang,K.Fu,Rating Correlated Topic Model:An Improved Latent Semantic Model for Collaborative Filtering. Journal of Computational Information Systems,2014,10(17):7259-7267.
[7]Y.Koren,R.Bell,Advances in collaborative filtering,Recommender Systems Handbook,2011,145-186.
[8]李慧,胡云,施珺.社会网络环境下的协同推方法[J].计算机应用,2013,33(11):3067-3070.
[9]郭磊,马军,陈竹敏.一种信任关系强度敏感的社会化推荐算法[J].计算机研究与发展,2013,50(9):1805-1813.
[10]D.D.Tu,C.C.Shu,H.Y.Yu.The Contextual Advertising Recommendation Algorithm Based on Joint Probability Matrix Decomposition[J]. Journal of software,2013,24(3)454-464.
[11]T.H.Zhou,H.h.Shan,et a1.Kernelized Probabilistic Matrix Factorization Exploiting Graphs and Side Information[C].Proceedings of the 12th International Conference on Data Mining,2012:403-414.
[12]Y.Koren,R.BeII,C.Volinsky.Matrix Factorization Techniques for Recommender Systems[J].ComputerSociety,2009,42(8)30-37.
[13]Y.Koren.Factor in the neighbors Scalable and Accurate Collaborative Filtering[J].ACM Transactionson Knowledge Discovery from Data(TKDD),2010,1(4)1-11.
[14]Y.S.Xu,J.W.Yin.Collaborative Recommendation with User Generated Content[J].Engineering Applications of ArtificialIntelligence 45(2015):281-294.
Collaborative Filtering Recommendation Algorithm Based on Matrix Factorization and User Social Relationships
ZHU Ai-yun
(School of Computer and Software Engineering,Weifang University of Science and Technology,Shouguang 262700)
Although matrix factorization(MF)based method has been successfully applied to collaborative filtering(CF).Recommender System(RS),it still suffers from data sparsity,cold start and other issues.In order to further improve the accuracy of the CF,integrates the social relationship among users into MF based CF.Based on singular value decomposition(SVD),the proposed method merged social friendships,the users rating bias and items rating bias into MF model.Designs a Stochastic Gradient Descent(SGD)algorithm to obtain potential user feature matrix and item feature matrix.Experimental results show that the proposed algorithm has good prediction accuracy,which is better than the existing algorithms.
Collaborative Filtering;Matrix Factorization;Recommender System;Gradient Descent
1007-1423(2016)25-0003-05DOI:10.3969/j.issn.1007-1423.2016.25.001
朱爱云(1977-),女讲师,硕士,研究方向为数据挖掘、推荐系统
2016-01-05
2016-09-01

