斜拉-悬索协作桥结合部合理设计研究
唐 亮,张 皓,刘玉擎
(1.中交公路规划设计院有限公司,北京 100088;2.中交公路长大桥建设国家工程研究中心有限公司,北京 100088;3.同济大学 土木工程学院,上海 200092;4.云南省交通规划设计研究院,云南 昆明 650011)
斜拉-悬索协作桥结合部合理设计研究
唐亮1,2,张皓4,刘玉擎3
(1.中交公路规划设计院有限公司,北京100088;2.中交公路长大桥建设国家工程研究中心有限公司,北京100088;3.同济大学土木工程学院,上海200092;4.云南省交通规划设计研究院,云南昆明650011)
为了研究斜拉-悬索协作桥斜拉段和悬索段的合理过渡问题,基于琼州海峡跨海通道的主跨3 000 m协作桥方案,采用有限元方法,分析了协作桥结合部受力机理,并进一步研究了交叉吊索数量、过渡段主梁刚度等参数的影响。结果表明,协作桥结合部设计需解决端吊索稳定受拉、端吊索活载索力幅可控、以及主梁刚度过渡平顺3个关键难题;增设交叉吊索数量可以有效改善结合部受力性能,增加过渡段主梁刚度效果有限且成本较高。
桥梁工程;结合部合理设计;有限元方法;斜拉-悬索协作桥;疲劳;松弛;刚度
0 引言
斜拉-悬索协作桥是在传统斜拉桥和悬索桥基础上发展起来的一种组合体系桥梁。中跨跨中部分采用悬索体系,可以解决斜拉体系悬拼过程中的静力稳定、气动稳定和主梁压力过大的问题;借助与斜拉体系的协作,可以提高悬索体系的刚度、降低主缆拉力和锚碇规模,尤其对深水和软土地基情况意义重大[1-4]。
从1883年罗勃林为提高悬索桥的刚度和抗风性能而提出用斜拉索增强悬索体系的构想至今,国内外桥梁工作者提出过多种协作体系形式。其中狄辛格提出的体系得到了较为广泛的认可,如图1所示,该体系在世界各地筹建的大跨度桥梁方案中被频繁地提出。1997年,由重庆交通学院等单位设计,我国在贵州乌江上建成了跨径为288 m的世界首座斜拉-悬索协作桥,实现了该桥型零的突破。
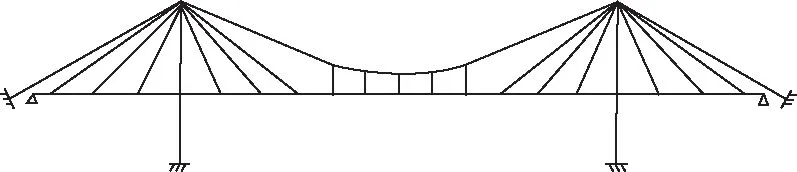
图1 狄辛格体系Fig.1 Dischinger system
然而,协作桥结构体系真正付诸实施的很有限,大部分处于方案设想和初步设计阶段,根本原因在于斜拉体系和悬索体系是两种受力形式完全不同的结构体系,其结合部位结构刚度变化大,结合区域的端吊索疲劳问题是学者关注的热点[5-10]。
本文以琼州海峡跨海通道的主跨3 000 m协作桥方案为例,首先提出了除控制结合部吊索活载索力幅外,结合部吊索稳定受拉和主梁刚度过渡平顺也是协作桥结合部设计的关键问题,并进一步研究了在吊拉结合部增设与斜拉索交叉的吊索、改变过渡段主梁刚度等措施的影响。
1 协作桥结合部关键问题
在琼州海峡跨海通道工程可行性研究报告中,西线桥位主通航孔桥方案之一为主跨3 000 m的双塔斜拉-悬索协作桥,在文献[11]研究基础上,采用笔者提出的基于造价估算的协作桥概念设计方法,研究确定该桥型方案主跨由等效跨径1 344 m的斜拉体系与等效跨径1 656 m的悬索体系组合而成,吊跨比0.552,矢跨比0.1,主桥跨径组成为(230+384+3 000+384+230)m。桥塔采用混凝土门式塔方案,主梁采用扁平流线型双箱分离式断面。全桥总体布置如图2所示。本文以此方案为对象,对协作桥吊拉结合部合理布置问题进行研究。

图2 琼州海峡跨海通道主跨3 000 m协作桥方案(单位:cm)Fig.2 Scheme of Qiongzhou Strait combined bridge with a main span of 3 000 m (unit:cm)
采用商用有限元分析软件计算全桥结构在各种静力荷载工况下的结构受力反应,有限元模型如图3所示。

图3 有限元模型Fig.3 Finite element model
对于协作桥成桥状态,在文献[12]研究基础上,采用笔者提出的以成桥时桥塔和主梁的位移最小为优化目标,以斜拉索初始索力、主梁压重为主要施调变量的迭代方法确定。
作为研究基准,首先分析了吊拉结合部未增设与斜拉索交叉的吊索的情况,如图4所示。
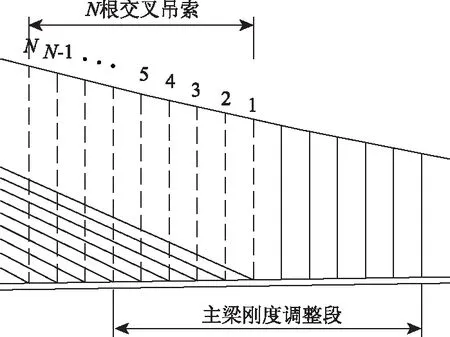
图4 吊拉结合部布置Fig.4 Arrangement of connection part
(1)吊索内力
图5给出了在各主要荷载及其组合作用下的吊索内力图(受拉为正),由于全桥的对称性,这里只给出了一半吊索的情况,吊索从桥塔向跨中顺序编号。由图5可见,对于各吊索控制工况(恒载+活载+温度)索力,最外侧吊索最大索力5 707 kN,约为一般吊索的1.6倍,然而其最小索力只有174 kN,远小于一般吊索的2 473 kN,吊索索力一旦出现负值,即表明吊索已松弛,退出工作,这对结构的整体受力是不利的。

图5 吊索内力图(无交叉吊索)Fig.5 Internal force curves of hangers (without intersecting hanger)
另外由图5可见,在汽车活载下,最外侧吊索活载索力幅达到4 890 kN,基本是一般吊索的5倍,疲劳荷载效应十分突出。
图6给出了吊索活载索力幅ΔF与控制索力最大值Fd之比(以下简称“活载效应比”)的情况。由图可见,最外侧吊索的活载效应比(即活载应力幅Δσ与控制应力最大值σd之比)达到0.86,远大于一般吊索的0.20。通常为满足吊索抗疲劳要求,需满足以下条件:
(1)
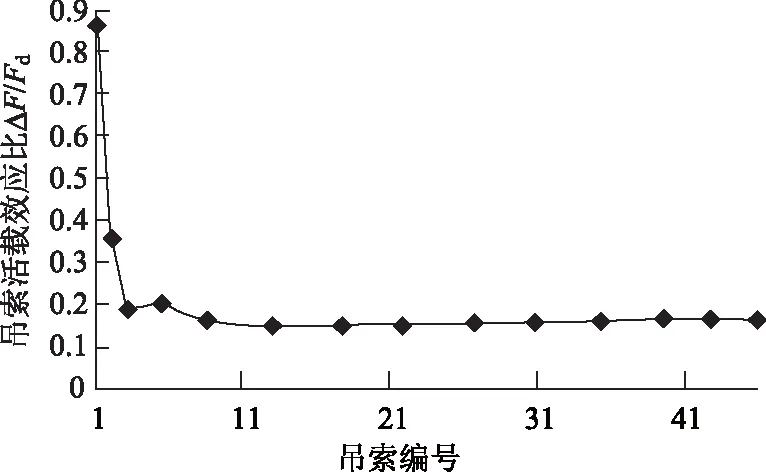
图6 吊索活载效应(无交叉吊索)Fig.6 Effect of live load on hangers (without intersecting hanger)
[9]的研究结果,一般情况下,含铁金属在交变应力下的耐久极限σf可取为拉伸试验中极限强度σu的0.45~0.55倍。考虑到尺寸效应及应力集中影响,本桥设计中偏于安全地取吊索耐久极限σf为其极限强度σu的0.3倍。另外,从吊索静力强度方面考虑,应有吊索控制应力最大值σd≤σu/K,其中K为吊索安全系数。因此,在保证吊索静力强度和疲劳耐久性的情况下,由式(1)可推得:
(2)
通常吊索安全系数取为2.5,则有:
(3)
由此可知,最外侧吊索已不能满足疲劳耐久性的要求。
(2)斜拉索内力
按照上述思路,对斜拉索内力进行了考察。图7给出了在各主要荷载及其组合作用下的斜拉索内力图,由于全桥的对称性,这里只给出了一半斜拉索的情况,斜拉索从边跨至跨中顺序编号。图8给出了斜拉索活载效应比的情况。
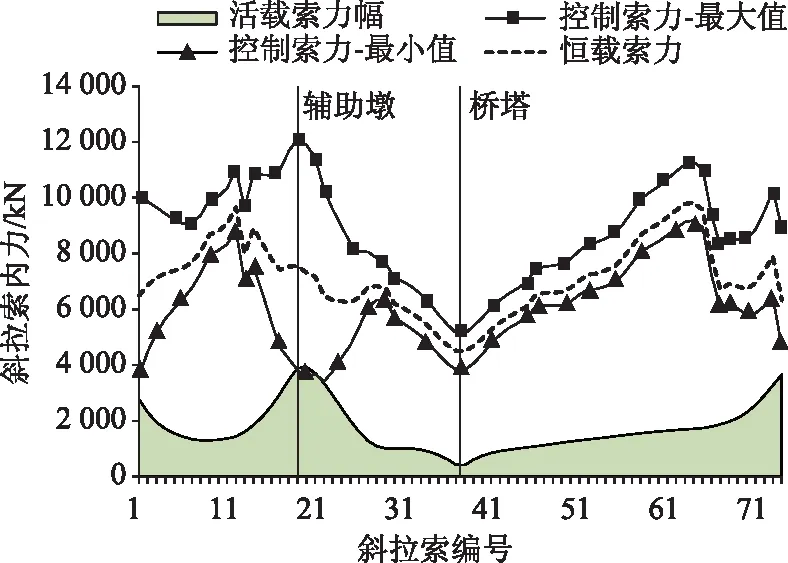
图7 斜拉索内力图(无交叉吊索)Fig.7 Internal force curves of stayed cables (without intersecting hanger)
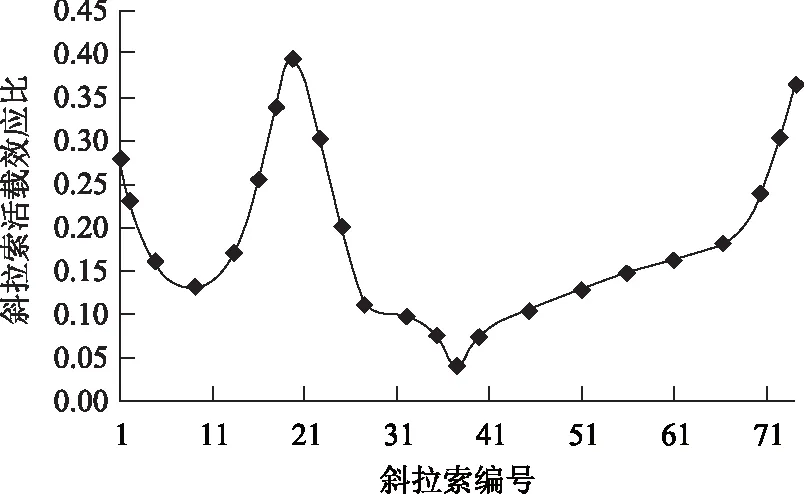
图8 斜拉索活载效应(无交叉吊索)Fig.8 Effect of live load on stayed cables (without intersecting hanger)
由图可见,边跨辅助墩处和吊拉结合部处的斜拉索活载索力幅较大,但其活载效应比不到0.4,根据式(3),所有斜拉索均能满足疲劳耐久性的要求。另外,所有斜拉索在最不利工况下的控制索力最小值均较充足,不会出现卸载松弛的情况。
(3)主梁变形
图9和图10分别给出了在汽车活载作用下的主梁竖向挠度和竖向转角包络图,由于全桥的对称性,这里只给出了一半主梁的情况,主梁节点从边跨至跨中顺序编号。由图可见,在中跨最外侧斜拉索(即吊拉结合部)附近,主梁活载竖向挠度包络曲线光滑,但其竖向转角包络曲线存在突变,表明在不设置交叉吊索的情况下,斜拉体系和悬索体系在结合部附近的主梁刚度过渡不平顺。

图9 主梁活载竖向挠度(无交叉吊索)Fig.9 Vertical deflection of girder under live load (without intersecting hanger)
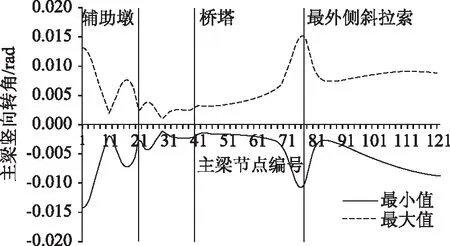
图10 主梁活载竖向转角(无交叉吊索)Fig.10 Vertical rotation angle of girder under live load (without intersecting hanger)
由以上分析可见,协作桥吊拉结合部的合理设计需解决以下3个关键问题:
(1)保证结合部吊索在汽车活载作用下不出现索力幅过大导致疲劳破坏的情况;
(2)保证结合部吊索在恒载+活载+温度的最不利荷载组合作用下始终不出现卸载松弛的情况;
(3)保证结合部主梁在活载作用下刚度过渡平顺,不出现较大的竖向转角突变。
在以往学者的研究中,通常只关注第1个问题,而忽略了第2、3个问题。
2 交叉吊索数量影响
已有研究结果表明,协作桥吊拉结合部增设与斜拉索交叉的吊索可以有效降低端吊索的活载索力幅[5-6]。围绕上述吊拉结合部合理设计的3个关键问题,下面对交叉吊索数量的影响进行了研究。
图11给出了端吊索索力随交叉吊索数量的变化曲线。由图可见,当交叉吊索数量由0根增加到1根,端吊索控制索力最小值由174 kN减小到-1 307 kN,出现严重的卸载松弛,这主要是由于在交叉区域内主梁恒载在斜拉索和吊索之间按1∶1进行分配,端吊索恒载储备索力大幅减小所致。此后,随交叉吊索数量的增加,端吊索控制索力最小值不断增大,当交叉吊索数量达到10根以后,由负变正,达到1 184 kN,恒载储备才较为充足,这一方面是由于最不利活载和温度引起的端吊索索力卸载量(=控制索力最小值-恒载索力)不断减小;另一方面也是由于随着交叉吊索伸入斜拉段长度的增加,主梁自重有所增加,端吊索恒载索力增大所致。
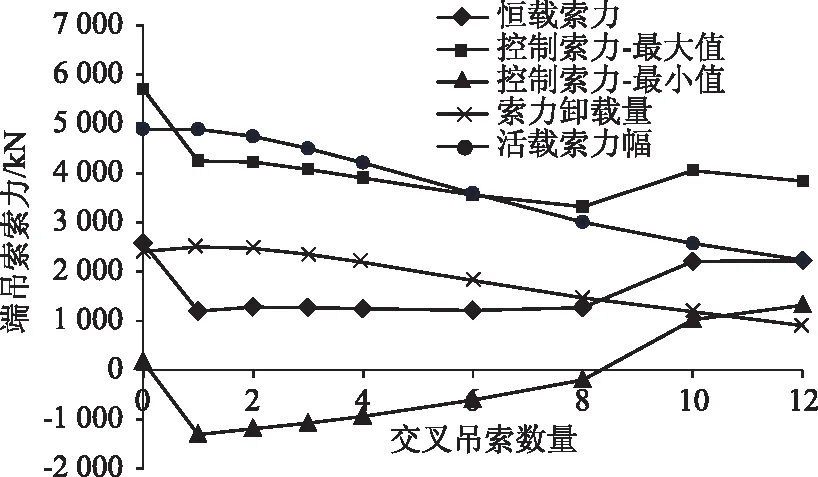
图11 端吊索索力Fig.11 Internal forces of end hangers
由图11还可见,随交叉吊索数量的增加,端吊索活载索力幅显著减小,相比0根交叉吊索,12根交叉吊索的端吊索活载索力幅减小约54.4%。
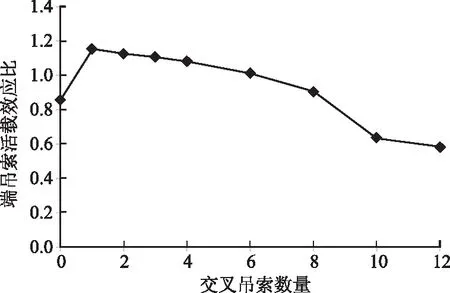
图12 端吊索活载效应Fig.12 Effects of live load on end hangers
图12给出了端吊索活载效应比随交叉吊索数量的变化曲线。由图12可见,当交叉吊索数量由0根增加到1根,由于端吊索恒载储备索力的减小,端吊索活载效应比由0.86显著增加到1.15。此后,随交叉吊索数量的增加,端吊索活载效应比不断减小,当交叉吊索数量达到10根,该值减小到0.63,根据式(3),此时端吊索才能满足疲劳耐久性的要求。
图13给出了在汽车活载作用下的吊拉结合部主梁竖向转角幅值随交叉吊索数量的变化曲线。由图可见,随交叉吊索数量的增加,吊拉结合部主梁竖向转角幅值不断减小,当交叉吊索数量达到8根以后,曲线变化非常平缓,表明斜拉体系和悬索体系在结合部附近的主梁刚度已过渡平顺。不同交叉吊索数量下的主梁活载竖向转角包络图见图14。
综上所述,对于主跨3 000 m的双塔斜拉-悬索协作桥方案,在吊拉结合部增设10根与斜拉索交叉的吊索是适宜的,可以同时满足结合部吊索稳定受拉、活载索力幅可控、以及主梁刚度过渡平顺的要求。
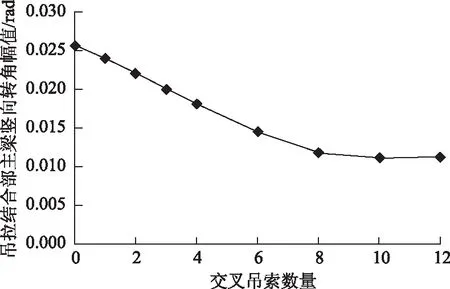
图13 结合部主梁竖向转角幅值Fig.13 Vertical rotation angle amplitude of girder in connection part
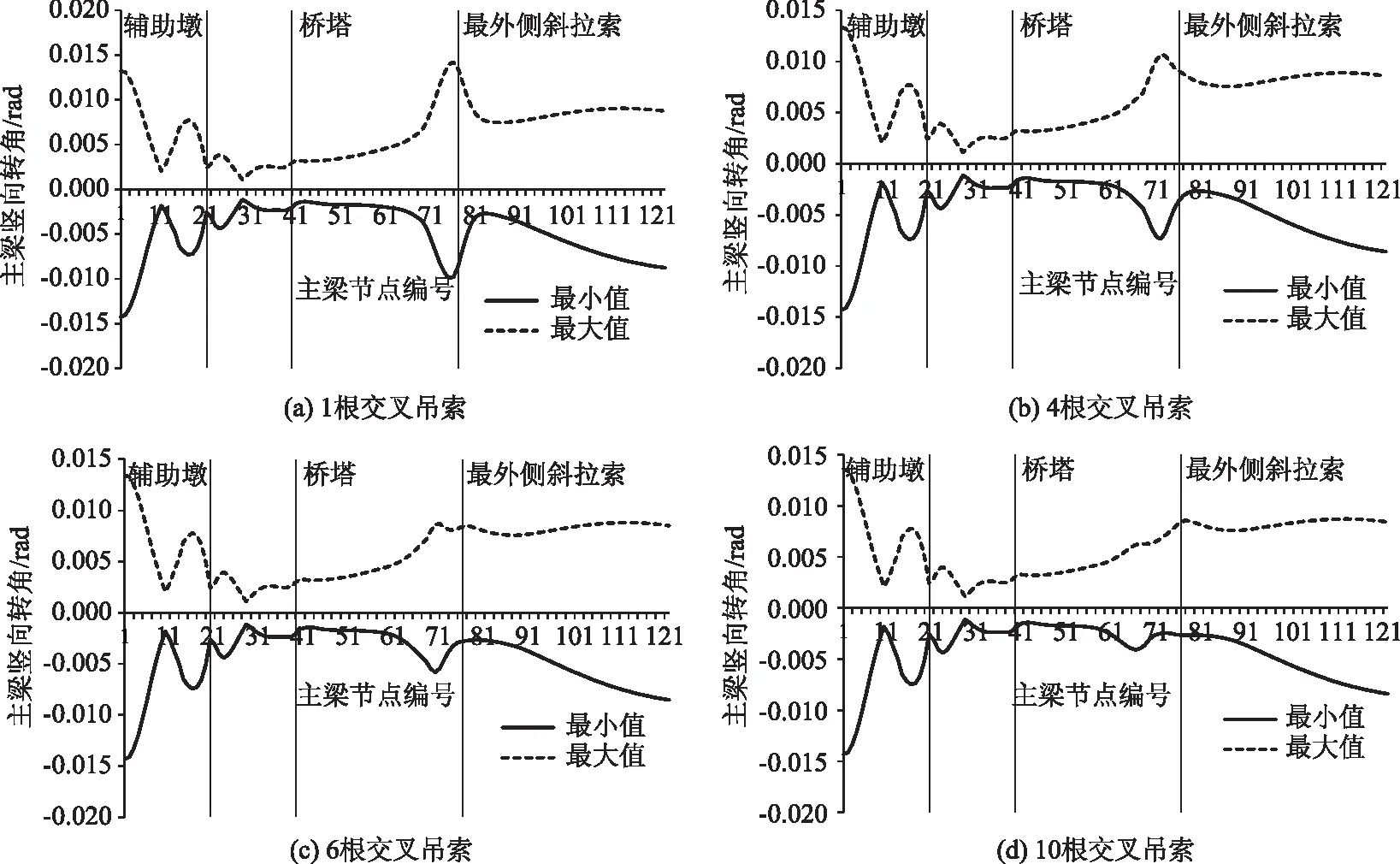
图14 主梁活载竖向转角Fig.14 Vertical rotation angle of girder under live load
实际上,在保证主梁刚度过渡基本平顺的情况下,结合部吊索稳定受拉及活载索力幅可控的要求都是容易满足的,如可以在吊点处增加配重,以增大吊索的恒载索力,同时减小活载效应比;或是提高吊索的安全系数,即增加吊索的截面面积,以增大活载效应比允许值(式(2)等号右侧项)。
3 主梁刚度影响
为改善协作桥斜拉体系与悬索体系结合部的结构性能,调节结合部过渡段的主梁刚度也是容易想到的措施。下面以吊拉结合部未增设交叉吊索的情况为基准,研究了过渡段内主梁刚度的影响,过渡段共取了11个梁段,如图14所示。
图15和图16分别给出了端吊索索力和活载效应比随过渡段主梁刚度的变化曲线,其中横坐标“过渡段主要相对刚度”是指调整后过渡段主梁刚度与原方案过渡段主梁刚度之比。由图可见,随过渡段主梁刚度的增加,端吊索控制索力最小值增加,端吊索活载索力幅减小,当过渡段主梁刚度增加为原方案的2倍后,前者只有350 kN,出现卸载松弛的风险仍较大,后者只减小了6.4%,活载效应比0.83,仍难以满足式(3)的疲劳耐久性要求。

图15 端吊索索力Fig.15 Internal forces of end hangers
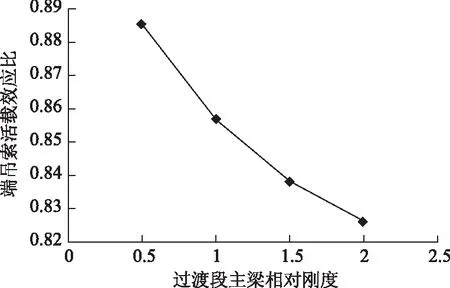
图16 端吊索活载效应Fig.16 Effects of live load on end hangers
图17给出了在汽车活载作用下的吊拉结合部主梁竖向转角幅值随过渡段主梁刚度的变化曲线。由图可见,随过渡段主梁刚度的增加,吊拉结合部主梁竖向转角幅值不断减小,过渡段主梁刚度增加为原方案的2倍后,该值减小17.2%,其效果与设置2根交叉吊索基本相当。

图17 吊拉结合部主梁竖向转角幅值Fig.17 Vertical rotation amplitude of girder in connection part
由以上分析可见,增加结合部过渡段主梁刚度可以改善协作桥斜拉体系与悬索体系结合部的结构性能,但效果较为有限,同时增大主梁刚度将不可避免地增加主梁材料用量,成本很大,因此一般不建议采用该措施。
4 结论
本文开展了斜拉-悬索协作桥结合部合理布置研究,主要结论如下:
(1)大跨径斜拉-悬索协作桥吊拉结合部的合理设计需解决结合部吊索稳定受拉、活载索力幅可控、以及主梁刚度过渡平顺3个关键问题。
(2)在吊拉结合部增设与斜拉索交叉的吊索是解决上述问题的有效手段。对于主跨3 000 m的双塔斜拉-悬索协作桥方案,在吊拉结合部增设10根与斜拉索交叉的吊索是适宜的。
(3)增加结合部过渡段主梁刚度可以改善协作桥结合部的结构性能,但效果较为有限,同时考虑成本问题,因此一般不建议采用该措施。
另外,在保证主梁刚度过渡基本平顺的情况下,结合部吊索稳定受拉及活载索力幅可控的要求都是容易满足的,如可以在吊点处增加配重,以增大吊索的恒载索力,同时减小活载效应比;或是提高吊索的安全系数,即增加吊索的截面面积,以增大活载效应比允许值。
参考文献:
[1]GIMSING N J.Cable Supported Bridges:Concept and Design[M].3rd ed.Chichester:John Wiley &Sons Ltd,2012.
[2]王伯惠.斜拉-悬索协作体系桥[J].辽宁省交通高等专科学校学报,2000,2(3):1-7.
WANG Bo-hui.Combined Cable-stayed and Suspension Bridges[J].Journal of Liaoning Provincial College of Communications,2000,2(3):1-7.
[3]王伯惠.斜拉-悬索协作体系桥(续)[J].辽宁省交通高等专科学校学报,2000,2(4):1-7.
WANG Bo-hui.Combined Cable-stayed and Suspension Bridges (Continued)[J].Journal of Liaoning Provincial College of Communications,2000,2(4):1-7.
[4]张新军,张丹.吊拉组合体系桥的研究进展[J].浙江工业大学学报,2007,35(5):553-558,585.
ZHANG Xin-jun,ZHANG Dan.Research Progress on the Cable-stayed-suspension Hybrid Bridges[J].Journal of Zhejiang University of Technology,2007,35(5):553-558,585.
[5]蒙云,刘东,孙淑红.大跨度P-F-C吊拉组合桥设计研究[J].重庆交通学院学报,1999,18(4):8-12,39.
MENG Yun,LIU Dong,SUN Shu-hong.P-F-C Large-span Combined Cable-stayed Suspension Bridge’s Study in Design[J].Journal of Chongqing Jiaotong Institute,1999,18(4):8-12,39.
[6]孙淑红,蒙云.吊拉组合桥交接区域吊索的疲劳问题研究[J].重庆交通学院学报,1999,18(4):13-18.
SUN Shu-hong,MENG Yun.The Boom’s Fatigue in Joint Area of Combined Cable-stayed Suspension Bridge[J].Journal of Chongqing Jiaotong Institute,1999,18(4):13-18.
[7]肖汝诚,项海帆.拉悬吊协作桥的施工控制与吊索疲劳控制研究[J].同济大学学报,1999,27(2):234-238.
XIAO Ru-cheng,XIANG Hai-fan.Study of Construction Control and Suspender Fatigue Problems for Cable-stayed Suspension Bridges[J].Journal of Tongji University,1999,27(2):234-238.
[8]肖汝诚,项海帆.斜拉-悬吊协作体系桥力学特性及其经济性能研究[J].中国公路学报,1999,12(3):43-48,116.
XIAO Ru-cheng,XIANG Hai-fan.Mechanics Characteristics and Economic Performances Study for Cable-stayed Suspension Bridges[J].China Journal of Highway and Transport,1999,12(3):43-48,116.
[9]肖汝诚,贾丽君,薛二乐,等.斜拉-悬吊协作体系的设计探索[J] .土木工程学报,2000,33(5):46-51.XIAO Ru-cheng,JIA Li-jun,XUE Er-le,et al.Research on the Design of Cable-stayed Suspension Bridges[J].China Civil Engineering Journal,2000,33(5):46-51.
[10]叶毅,张哲,李文武,等.自锚式吊拉协作体系桥端吊索破断效应[J].沈阳建筑大学学报:自然科学版,2013,29(3):412-418.
YE Yi,ZHANG Zhe,LI Wen-wu,et al.Fracture Effects Analysis of End Hanger of Self-anchored Cable-stayed Suspension Bridge[J].Journal of Shenyang Jianzhu University :Natural Science Edition,2013,29(3):412-418.
[11]孙斌,肖汝诚,贾丽君,等.斜拉-悬吊协作桥经济性能研究[C]//第十四届全国桥梁学术会议论文集.上海:同济大学出版社,2000:542-549.
SUN Bin,XIAO Ru-cheng,JIA Li-jun,et al.Economical Behavior of Cable-stayed Suspension Bridge[C]//14th National Conference on Bridge.Shanghai:Tongji University Press,2000:542-549.
[12]朱巍志,张哲,潘盛山,等.自锚式斜拉-悬索协作体系桥合理成桥状态确定的分步算法[J].土木工程学报,2010,43(10):91-97.
ZHU Wei-zhi,ZHANG Zhe,PAN Sheng-shan,et al.Stepwise Method of Calculation for the Rational Finished State of Self-anchored Cable-stayed Suspension Bridges[J].China Civil Engineering Journal,2010,43(10):91-97.
Research on Rational Design of Connection Part for Combined Cable-stayed and Suspension Bridge
TANG Liang1,2,ZHANG Hao4,LIU Yu-qing3
(1.CCCC Highway Consultants Co.,Ltd.,Beijing 100088,China;2.National Engineering Research Centre,CCCC Highway Bridges Co.,Ltd.,Beijing 100088,China;3.School of Civil Engineering,Tongji University,Shanghai 200092,China; 4.Yunnan Transport Planning and Design Research Institute,Kunming Yunnan 650011,China)
To study the rational transition between the cable-stayed segment and the suspension segment in a combined cable-stayed and suspension bridge,based on the scheme of Qiongzhou Strait combined bridge with a main span of 3 000 m,the working mechanism of the connection part is analyzed by finite element method.The effects of parameters such as the number of hangers intersecting with stayed cables and the stiffness of transition girder are studied.The result shows that (1) 3 key problems should be solved in the design of the connection part:the end hangers should always be in tension,the force amplitudes of the end hangers should be in control,and the stiffness transition of girder should be smooth; (2) increasing the number of intersecting hangers can effectively improve the structural performance of the connection part,while the effect of raising the girder stiffness is not distinct with high cost.
bridge engineering;rational design of connection part;finite element method;combined cable-stayed and suspension bridge;fatigue;relaxation;stiffness
2015-06-04
交通运输部科技项目(2011 318 494 160);国家高技术研究发展计划(八六三计划)项目(2012AA112501)
唐亮(1981-),男,北京人,博士,高级工程师.(TangL03@126.com)
10.3969/j.issn.1002-0268.2016.01.11
U441+.4
A
1002-0268(2016)01-0070-06

