寻找教学起点,实现教与学的有效链接
何心芳

《义务教育数学课程标准》(2011年版)中指出:“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上”。这说明教师必须充分了解学生的知识体系和活动经验后才能组织教学,否则教师的教学就只是一厢情愿。
一、教学片段再现
【课堂实录】
师:同学们还记得三角形内角和的结论吗?
生:记得,180°。
师:还有同学记得是怎么得到这个结论的吗?
(沉默了好大一会儿,终于有几个学生想到了)
生:把3个角拼在一起。
师:老师这里有一个三角形。你给大家演示一下吧!
(学生上讲台操作)
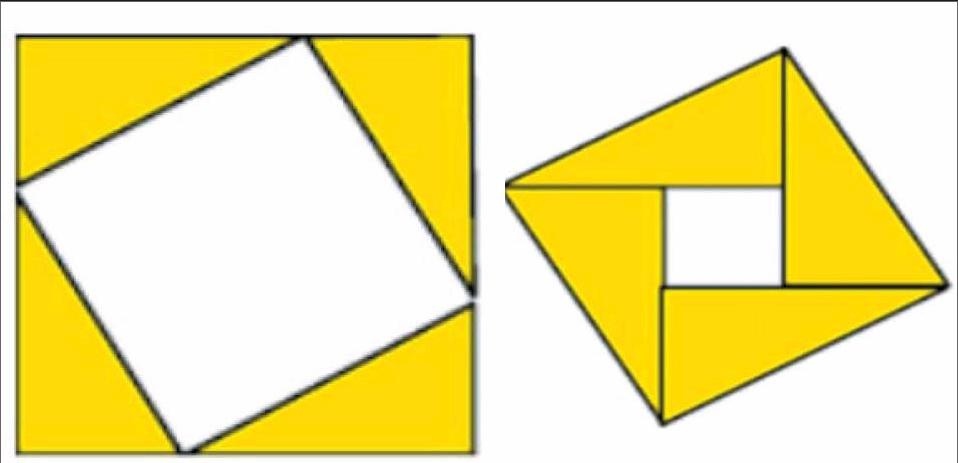
师:很好。但拼图毕竟是有误差的。我们今天将用几何推理的方法来说明三角形内角和为180°的原因。请同学们看这种拼图方法:如图①,我们可以看出图②中,除了∠3的位置没有变化以外,∠A、∠B的位置都发生了变化,你能发现变化后的∠A、∠B(即∠1、∠2)与原来位置的关系吗?
生:∠A和∠1是内错角,∠B和∠2是同位角。
师:很好。∠A和∠1是相等的,所以AB//CD。从而我们就寻找到解决问题的方法。即过点C作CD//AB……
【产生困惑】这节课看似是在教师的引导下得出了证明结论的方法,但存在几个问题:学生对于这个结论是相当熟悉的,而对于它的说明方法已经忘记了。初中教材的要求是让学生通过拼图来体会图形的变换,从而找到说明该结论正确的理论依据。那么这样的设计达到教学要求了吗?学生上讲台演示的拼图方法应该不止一种。为什么老师只选择了这一张?对于初学几何语言的学生来说,辅助线如何添加真的能理解吗?
【分析原因】学生的学习起点可分为逻辑起点和现实起点。其中逻辑起点是指学生按教材、文本、课标的规定,应该具有的知识、能力基础,而现实起点是指学生在多种学习资源的共同作用下,已实际具有的知识能力、情感态度基础。教材在编排上十分注意对知识、能力的逻辑衔接,这是从学生学习的逻辑起点来设计教学内容的,它有效地防止了教学中的随意性。而我认为在实际教学中教师更需要了解学生的现实起点,充分利用学生所熟悉的、简明的、合理的知识,将学生已有的学习起点对接到我们的教学起点上,方能引向知识的本质,达到教学的最终目的。
二、我们可以这样做
1.分析教学内容是否前后有关联,找到新旧知识的对接点
数学教学必须建立在学生已有的知识经验和认知能力的基础上,这就要求把握好学生的学习起点。对于每一节教学内容,要在新旧知识的衔接点上思考学生已掌握了哪些知识,已具备哪些活动经验,并在此基础上设计教学起点,确定本节课的生长点,产生知识的迁移。
【案例1】分式的加减(1)
师:同学们还记得同分母的分数如何加减吗?你能举例说明吗?
(学生思考一小会儿,有个别学生举手)
生:分母不变,分子相加减……
师:你认为同分母的分式应该如何加减?
生:分母不变,分子相加减。
师:类比同分母分数相加减,我们可以得出同分母的分式相加减的法则……(板书法则)
师:我们用法则尝试计算下列几个算式。
【案例修改】
师:同学们会计算下列算式吗?
目的:唤起学生对于分数计算的回忆。第(1)小题主要是复习同分母分数加减的法则;第(2)小题意在提醒学生分数的结果要化成最简分数,即约分。
师:下面的算式你会计算吗?
反馈:第(1)小题没有任何问题;第(2)小题个别同学忘记约分。
师:你能看出这两个算式的特点吗?
生:都是两个分式在做加减运算。它们的分母是一样的。
归纳:同分母分式的加减法法则。
师:老师觉得 好难啊!怎么分母不一样啊?
【案例反思】虽然最后一个题目学生遇到的困难比较多,如分母的变形、结果的约分,但在这个过程中学生对于同分母分式的加减运算记忆是深刻的。因为分式和分数本身长得就比较像,通过比较教学,达到知识的迁移是可行的。而且这样的教学起点是对接在学生已有的知识基础上的,是在学生认知规律上的迁移,形成一个层层递进、由简到难的教学过程,取得的教学效果也是不错的。
2.观察教学内容是否和生活有联系,找到便于学生理解的对接点
在教材上经常会出现“上述图片中有你熟悉的图形吗”“……,生活中还有类似的例子吗”等提问。可见有些教学内容比较抽象,学生不易马上理解和想象。此时我们可以充分挖掘学生身边和生活中的实例,来帮助学生学习。
【案例2】图形的旋转主要是考查学生对图形变换的空间想象能力。要让一个图形运动起来,就必须要知道导致它运动的元素以及运动的方式。平时学生看到的书本上的几何图形都是平面的、静止的。而生活中的物体却有旋转的,所以我就从生活中旋转的物体导入开始理解什么是旋转。可以是实物,如电扇、车轮、钟摆等;也可以是图片,如摩天轮、秋千、雨刮器等。首先在学生的脑海里构建旋转现象,挖掘这些物体在旋转时的共同点,从而找到旋转的两个要素,即旋转中心和旋转方向。
这样的教学起点就是建立在学生的生活经验基础之上,让学生既感受到生活中隐藏着数学问题,又能利用数学知识解释生活现象。找到抽象的教学内容和学生的现实生活经验的对接点,让学生的数学学习经历能够贴近生活。虽然在学生的学习起点和教师的教学之间建立纽带要费些时间,但这样的时间是有价值的。
3.思考教学内容是否对于学生是全新的,找到教学方式和手段的对接点
为了能用更多的方法解决一些数学问题,有时需要格外补充一些以前不曾接触的教学内容。对于这种情况,我们可以充分利用现代化的教学设备或小组合作交流等方式来组织教学。
【案例3】在进行《勾股定理》教学时,教师先问了一下学生是否听说过“勾股”,结果学生在提醒下想起了勾3股4弦5。而作为数学史上的重要定理之一,教师不仅要让学生知道勾股定理,会用勾股定理,还要让学生了解和实践这一定理的成长和证明过程。对于这样一个全新的数学知识,仅用简单告知是无法达到目的的,所以我在上新课前布置了一项作业:充分利用网络资源,搜集勾股定理的历史和科学家们在验证该定理时的奇思妙想。
师:同学们,今天我们这节课主要研究勾股定理。有谁知道什么是“勾”“股”?它是怎么来的?
学生从古代的《周髀算经》说到赵爽弦图,再到2002年世界数学家会会标……
师:到目前为止,有多少种验证方法?
学生认为下列3种方法还可以理解,其他的有难度。
师:请同学来当一回数学家,演示验证的过程。
像这样以学生自主学习,交流学习、体会作为教学的起点,不仅能促使学生感受数学文化的内涵,提高他们的动手实践能力,还可以使其感受数学学习的魅力,感叹数学思维的灵活。
三、我们还可以做得更多
由于学生个体的差异性和学习资源的多样性,学生的学习起点也就各不相同,那么课堂教学的起点还可以如何寻找呢?除了常规的方法,如问卷法、聊天法、测试法外,我们还可以尝试问题交流法。
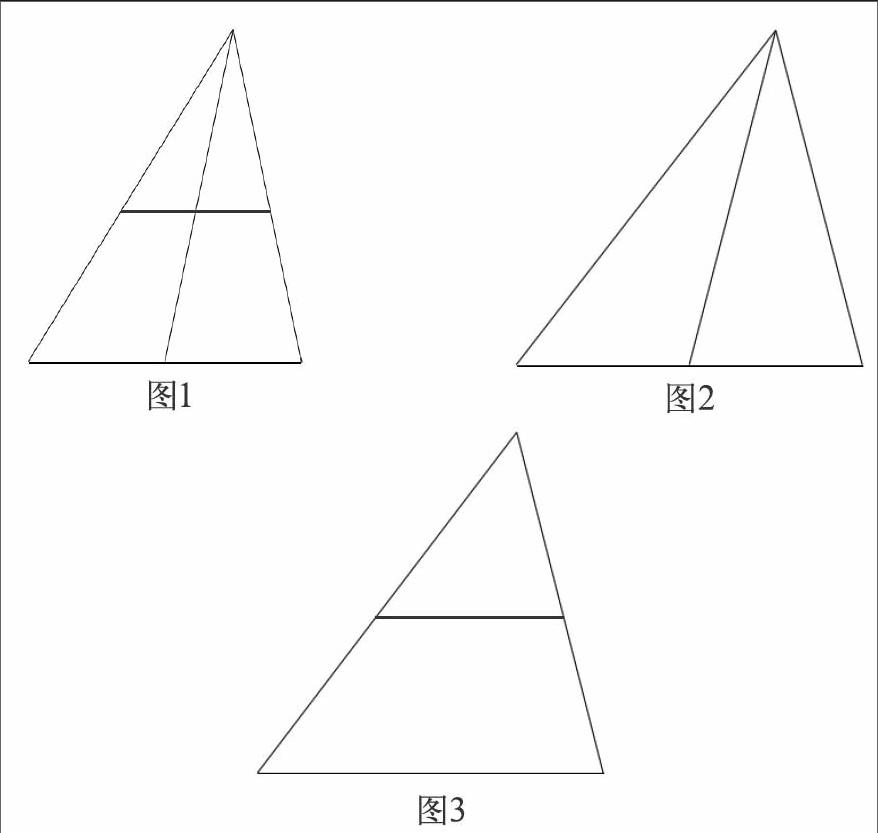
【案例4】中位线的内容结束后,学生提出了中线和中位线是否有关系的问题。我的做法是:利用学生提供的图形(图1)分解出两幅图(图2和图3)。先理清概念,再利用图2结合三角形的变化,回顾等腰三角形底边上的中线和直角三角形斜边上的中线性质(数量关系),利用图3复习三角形中位线的性质(数量关系和位置关系)。然后研究中线和中位线分原三角形所得的小三角形和原三角形的面积关系。最后利用图3延伸出中点三角形及相关性质。
总之,我们要直面学生的数学现实,站在学生的角度寻找学生的学习起点和教师的教学起点的对接点。无论这两点之间是直线、曲线还是折线,它都将是一幅最美的几何图形,蕴含着师生的共鸣和智慧。

