基于鸡群优化算法的旁瓣抑制滤波器设计

邱　攀，王　展

（国防科学技术大学 电子科学与工程学院，湖南 长沙 410073）

基于鸡群优化算法的旁瓣抑制滤波器设计

邱攀，王展

（国防科学技术大学 电子科学与工程学院，湖南 长沙 410073）

文章针对相位编码雷达的距离旁瓣抑制问题，提出了基于鸡群优化算法的旁瓣抑制滤波器的设计方法。鸡群优化算法是一种全新的群智能优化算法，能够求解各类复杂的优化问题，具有良好的收敛性能，更容易找到全局最优值。最小峰值旁瓣（PSL）滤波器和最小积分旁瓣（ISL）滤波器的设计即为较复杂的优化问题，本文利用鸡群优化算法对这两种滤波器进行求解。实验仿真分析表明，通过鸡群优化算法设计的旁瓣抑制滤波器能有效地抑制距离旁瓣，并适用于各类编码信号。

二相编码；旁瓣抑制；智能优化算法

1　概述

二相编码雷达的距离旁瓣一直受到关注，二相编码良好的旁瓣特性对于降低虚警概率、提高雷达检测性能有着极大的意义，因此如何抑制旁瓣是二相编码作为脉冲压缩信号必须解决的问题。一般通过两大类方法来改善二相编码的旁瓣特性：编码优选和旁瓣抑制。编码优选是通过设计旁瓣性能好的码元，或者选择自相关性能优良的编码比如常见的巴克码和m序列，但这类方法受约束较多，设计出来的编码也很难广泛应用于工程实现。在实际应用中，当确定了编码的形式而回波信号主旁瓣比仍无法满足工程要求时，旁瓣抑制就成了主要的手段。旁瓣抑制通过设计滤波器来降低旁瓣以提高主旁瓣比，常用的方法有失配滤波器法等。该类方法中主要有最小二乘法［1-2］、线性规划法［3］、神经网络法［4］等。其中最小二乘法需要经过多次迭代，若是迭代终止条件选择不当或者迭代初始值选择不恰当会严重影响算法的效果。线性规划一般不适用于复信号。神经网络要求足够的训练样本量，而且收敛速度慢，无法在实际中广泛应用。

文献［5］提出了一种新的群智能优化算法，通过利用该算法对不同指标下的旁瓣抑制滤波器的系数进行求解。相比于其他求解算法，该算法具有收敛速度快和收敛精度高的优点，能快速找到全局最优点。通过仿真实现验证，利用该算法对常用的巴克码和m序列所求得的旁瓣抑制滤波器，其主旁瓣比相较于匹配滤波器有较大的提高，能够达到实际应用标准。

2　鸡群优化算法

鸡群优化（Chicken Swarm Optimization，CSO）算法［5］是一个全新的群智能优化算法，具有简单、良好扩展性的特点，是一种天然的多种群自适应算法，由XianbingMeng等在2014年10月提出。这种算法通过模拟鸡群的等级规则和鸡群的行为，提取出合适的模型来优化问题。整个鸡群被分成多个小群，每一个小群都包含一个公鸡、多个母鸡和多个小鸡，不同的鸡种有着不同的运动规律，在特定的等级规则下，不同的鸡之间都存在着竞争关系。

为了简便起见，我们理想化地设定鸡群的行为遵循以下规则［6］：

一个鸡群中有许多子群，一个子群又包含一只公鸡、很多只母鸡与小鸡。

根据鸡群自身的适应度值来划分子群以及确定鸡的种类。适应度值最优的一些个体划分为公鸡，而且每只公鸡都是它所在子群的领头；最差适应度值的个体划分为小鸡；其余的就是母鸡。母鸡随机选择一个子群来跟随，母鸡与小鸡之间的母子关系也是随机建立的。

鸡群中的等级规则、支配关系和母子关系会维持一段时间不变，这种状态只会在隔了G代后才开始更新。

子群中的母鸡和小鸡跟随着这个子群的公鸡搜寻食物；每个个体都可以防止鸡群中的其他个体抢夺自己的食物，每个个体也都能随机偷取其他个体的已经发现的食物；小鸡跟随自己的母亲搜寻食物；鸡群中具有等级地位越高的个体在食物竞争时具有更好优势。

假定RN，HN，CN和MN分别代表公鸡、母鸡、小鸡和妈妈母鸡的数目。鸡群中每个个体的位置xi,j（t）（i∈［1，…，N］，j∈［1，…，D］）表示第i个个体的j维在第t次迭代的值，N是鸡群个体的总数目，D是鸡群寻找食物的空间的维数。

鸡群个体在寻找食物时的位置的更新公式因其所属种类不同而不同。在使用食物时，相较于差一点的适应度值的公鸡，更好适应度值得公鸡有着优先权。也就是说适应度值越好的公鸡中有着更优的竞争优势，它们可以在更广泛的空间寻找食物。这种模型可用以下公式表明：

式中：Randn（0，σ2）是均值为零，标准差为σ2的高斯分布；ε是一个极小的常数，避免除数为零；k表示鸡群中公鸡的任一个体；f表示对应个体的适应度值。

母鸡跟随自己所在子群的公鸡搜寻食物，也能随机偷取其他个体的食物。同样，在竞争食物时，适应度值好的母鸡比适应度值差的母鸡更具有优势。这种模型用以下数学公式表示：

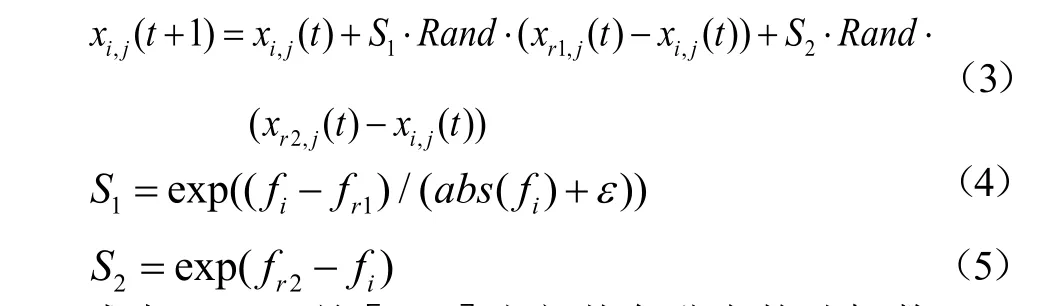
式中：Rand是［0，1］之间均匀分布的随机数；r1∈［1，…，N］为第i只母鸡自身所在子群中的公鸡；r2∈［1，…，N］是从鸡群（公鸡和母鸡）中随机挑选的个体，且r1≠r2。

小鸡跟随自己的母亲搜寻食物，它们的位置更新公式如下：

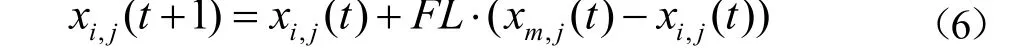
式中：xm，j（t）表示第i只小鸡对应的母鸡的位置；FL（FL∈（0，2））为跟随系数，表示小鸡会跟随母鸡搜寻食物。考虑到个体的差异，每个小鸡对应的FL取（0，2）之间的随机数。

算法的具体流程如下：

初始化鸡群，给出各个鸡种的数目RN，HN，CN和MN以及鸡群运动的空间维数D和鸡群位置更新频率G等；

计算鸡群的初始适应度值fitness，以及当前的全局最优值fMin和全局最优值的位置bestI，t=1；

若mod（t，G），鸡群开始更新，对ftness进行排序，建立新的鸡群的等级制度，将鸡群划分为多个子群并选择母鸡和小鸡的对应关系；

根据式（1）、式（3）和式（6）分别对公鸡、母鸡和小鸡的位置进行更新并分别计算每个个体的适应度值；更新鸡群的个体当前全局最优值和全局最优值的位置；t=t+1，若满足迭代停止条件，则停止迭代，输出最优值，否则转到（3）。

要注意的是，其中G的取值对此算法的收敛精度和收敛速度有着重要的影响。G的值太大，算法收敛速度慢，不能快速收敛到全局最优值；G的值太小，算法容易陷入局部最优值。经过多次测试后，一般G∈［2，20］时，算法对于大多数问题的优化，在保证收敛精度的同时，收敛速度也比较高。

3　旁瓣抑制滤波器设计

假设雷达发射信号是由码长为N，时宽为T，带宽为B的相位编码信号。对回波信号以码元速率进行采样得到复序列｛xk｝，其中k=0，1，…，N-1。设计的M（M≥N）阶滤波器的权系数用｛wm｝表示，其中m=0，1，…，M-1。将复序列｛xk｝两端补零得到的信号序列记为｛sm｝，m=0，1，…，M-1，写成向量形式为［7］：

则滤波器的输出为：

上式中当n-i＜0以及n-i≥M时sn-i=0。

式（2）用向量表示为：Y=XHW （9）

其中：

我们设定n=M-1时为滤波器输出的主瓣峰值的位置［8］，对峰值旁瓣最小化约束可得到最小峰值旁瓣滤波器（PSL），最小峰值旁瓣抑制滤波器为满足下式约束的W：

在此信号模型下，最小积分旁瓣（ISL）滤波器为满足下式约束的W：

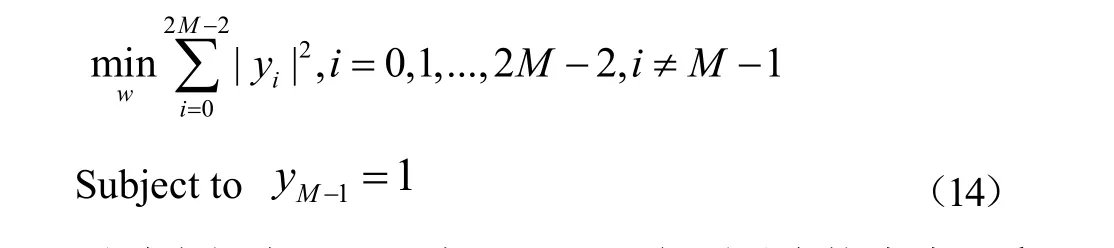
通过求解式（13）、式（14）即可得到对应的滤波器系数，但是一般来说并没有解析的求解方法。针对式（13）、式（14）的求解问题，通过利用鸡群优化算法可以得到很好的解决。鸡群优化算法通过判断鸡群个体的适应度函数值来判断位置的优劣。因此分别选择式（13）和式（14）作为最小峰值旁瓣滤波器和最小积分旁瓣滤波器的适应度函数［9］，适应度函数值越小，则说明鸡群个体的位置对应着更好的滤波器系数。算法在满足迭代停止条件后停止迭代，输出的最优值即为滤波器的系数。

4　仿真实验及其性能分析

利用文中的算法对常见的13位巴克码和31位m序列设计最小峰值旁瓣滤波器和最小积分旁瓣滤波器。其中鸡群数量为N=100，公鸡、母鸡占种群数量的比例分别为0.2和0.6，剩下为小鸡，其中母鸡中妈妈母鸡的比例为0.1。按照经验，更新频率G=10，FL∈［0.4，1］。D的取值即为所求滤波器的长度。实验中，每次程序随机运行50次，记录下每次运行的最优解，最后选择50次结果中最好的最优解作为滤波器的系数。

4.1 对13位巴克码设计最小峰值旁瓣滤波器和最小积分旁瓣滤波器

图1中（a）和（b）分别是匹配滤波器与利用鸡群优化算法设计的最小峰值旁瓣抑制滤波器（滤波器长度为13）的滤波结果对比。匹配滤波器的峰值旁瓣电平为-22.28dB，积分旁瓣电平为-22.97dB，设计的滤波器对应的峰值旁瓣和积分旁瓣电平分别为-25.15dB和-31.36dB。可见在滤波器长度相同的时候，利用本文的算法设计的滤波器相较于匹配滤波器对脉压输出后的峰值旁瓣的抑制有着更好的效果，对于主瓣能量的积累也有着较好的效果。

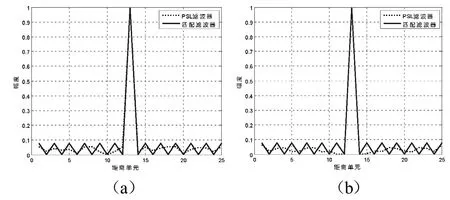
图1 13位巴克滤波器输出效果比较

图2—3分别是峰值旁瓣值和积分旁瓣值随滤波器长度的变化情况，可见随着滤波器长度的增加，峰值旁瓣和积分旁瓣都能显著地减小。

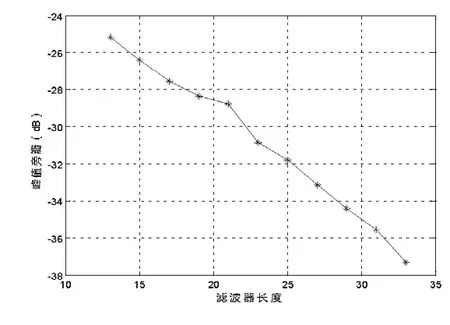
图2 峰值旁瓣值随滤波器长度的变化

图3 积分旁瓣值随滤波器长度的变化

4.2 对31位m序列设计最小峰值旁瓣滤波器和最小积分旁瓣滤波器

图4—5分别为采用本文所述方法设计的31位m序列的最小峰值旁瓣滤波器和最小积分旁瓣滤波器的效果随滤波器长度的变换情况。可以看出，对于m序列本文所述方法同样能够有效地抑制距离旁瓣，也能有效地降低积累旁瓣能量。但是随着滤波器阶数的增加，最小峰值旁瓣电平和最小积累旁瓣电平最后会保持在某一固定值，主要是因为滤波器长度过长，鸡群优化算法对于高维的优化问题的求解具有一定的局限性，可以通过引入惯性权值和学习因子来提高算法对于高维问题的优化能力，从而进一步提高滤波器的旁瓣抑制效果。

图4 峰值旁瓣值随滤波器长度的变化

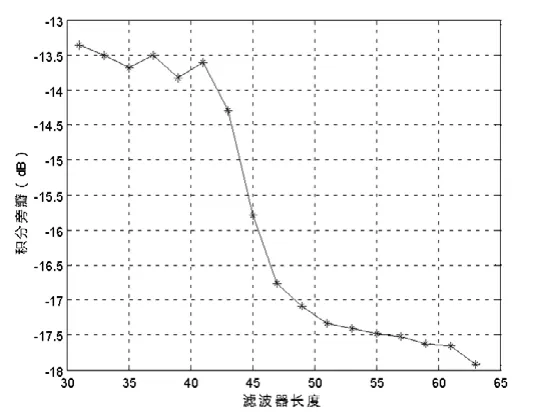
图5 积分旁瓣值随滤波器长度的变化

5　结语

本文针对在设计相位编码旁瓣抑制滤波器时，难以通过有效的解析方法求得滤波器系数的问题，采用一种全新的群智能优化算法来对滤波器系数进行求解。该方法具有收敛精度高、收敛速度快等优点，仿真实验验证了方法对旁瓣抑制的有效性。同时该方法适用于各类相位编码信号。需要注意的是，评判滤波器的性能指标有多种，因而在实际应用中需要综合考虑各方面的因素。

［1］位寅生，沈一鹰，刘永坦.一种基于最小二乘的高频雷达信号处理方法［J］.系统工程与电子技术，2001（1）：34-36.

［2］杨斌，向敬成，刘晟. 一种数字脉压旁瓣抑制滤波器设计方法［J］.电子科学学刊，2000（1）：124-129.

［3］ZORASTER S. Minimum Peak Range Sidelobe Filters for Binary Phase coded Waveform［J］.Aerospace and Electronic Systems， 1980（1）：112-115.

［4］孔祥维，黄申，李国平.基于小波和神经网络的二相编码旁瓣抑制的研究［J］.系统工程与电子技术，2001（6）：1-3.

［5］MENG X B，LIU Y，GAO X Z，et al.A new bio-inspired algorithm： chicken swarm optimization［C］5th International Conference on Swarm Intelligence. Hefei： Springer International Publishing， 2014.

［6］孔飞，吴定会. 一种改进的鸡群算法［J］. 江南大学学报（自然科学版），2015（6）：14.

［7］何学辉，曾操，苏涛，等.基于二阶锥规划的峰值旁瓣抑制滤波器设计［J］. 系统工程与电子技术，2009（11）：2567-2570.

［8］王飞雪，欧刚.恒增益处理损失的最佳编码旁瓣抑制滤波器［J］.电子学报，2003（9）：1418-1421.

［9］方伟.群体智能算法及其在数字滤波器优化设计中的研究［D］.无锡：江南大学，2008.

Design of sidelobe suppression flter based on Chicken Swarm Optimization Algorithm

Qiu Pan， Wang Zhan
（Electronic Science and Engineering College of National University of Defense Technology， Changsha 410073， China）

A design method of sidelobe suppression flter based on chicken swarm optimization （CSO） algorithm is proposed to solve the problem of range sidelobe suppression of bi-phase coded radar. Chicken swarm optimization algorithm is able to solve many complex problems， which is a new swarm intelligence algorithm. CSO is able to avoid premature convergence and can fnd the global optimum easily. Designing PSL filter and ISL filter are complex optimization problems. In this paper， CSO is used to solve the problem. The experimental and simulation analysis proved that flter designed in this paper can effectively suppress the sidelobe， and this method is suitable for all kinds of coded signals.

Bi-phase codes；sidelobe suppression；intelligence optimization algorithm

邱攀（1992— ），男，湖南常德。