Elastic Net方法在纵向数据模型中的应用*

许丽庆田凯熊琴

（1.广西大学数学与信息科学学院，南宁，530004；2.广西科技大学医学院，柳州，545006）

Elastic Net方法在纵向数据模型中的应用*

许丽庆1田凯1熊琴2

（1.广西大学数学与信息科学学院，南宁，530004；2.广西科技大学医学院，柳州，545006）

将Elastic Net方法（EN方法）运用于平衡纵向数据模型的变量选择中，建立了相应的纵向数据模型，证明了平衡纵向数据模型的EN估计具有组效应性质，通过数值模拟比较EN方法和Lasso方法，表明EN方法在处理强相关变量时因其能将强相关变量全部选入纵向数据模型而优于Lasso方法.

Elastic Net方法 纵向数据模型 变量选择 组效应性质

1　引言

纵向数据自提出以后在社会科学，心理学，生物医学，计量经济学等领域普遍存在.通过对观测对象中的每一个受试个体或者每一个受试单位在不同时间点上重复观测得到的数据称为纵向数据.因此数据即包含同一时间点上不同样本的数据，也包含不同时间点上的观测数据.所以，纵向数据把截面数据和时间数据有效的结合在一起，既能够很好地分析出个体随时间变化的趋势，又能很好的反映个体间的差异及个体内的变化趋势.

关于纵向数据的研究一直是统计研究的热点，其中变量选择问题一直受到广泛的关注.为了选择重要的变量和增强预测精度，统计学家们经常应用不同的方法，例如逐步回归法和子集选择法，但是由于这两种方法算法的不稳定性［1-2］，导致它们的理论性不强.1970年，由Hoerl和Kennard［3］提出的岭回归虽然增加了稳定性可是它并不能将任何系数设置为零，所以其不能给出一个简单的解析模型.1996年，Tibshirani［4］提出的Lasso方法，它可以同时做到变量的选择和参数估计.2005年，Zou和Hastie［5］提出的Elastic Net（EN）方法，它是Lasso方法的一种有效改进，它在处理变量间存在组效应的数据方面要显著优于Lasso法.

当每个受试个体重复观测的次数和时刻相同就得到了平衡纵向数据，平衡纵向数据模型要求自变量之间相互独立，至少不允许出现很强的相关性，同时还要求所研究的样本量n大于预测变量个数p，但是现实生活中往往出现p≫n的情形，所以在处理高维度且变量间有强相关性的纵向数据时，传统的纵向数据就不再适用了.本文将EN方法用于纵向数据模型，建立相应的纵向数据模型，对高维度强相关的变量选择问题进行了有益的探索.

2　平衡纵向数据模型和EN方法

2.1平衡纵向数据模型

平衡纵向数据要求对每个个体重复观测的次数相同，因此每个个体内部数据的个数相同且同分布，对第i个个体的响应变量和p个预测变量重复观测n次可得到：

多数的纵向数据分析都是基于回归模型基础上的，如线性模型.对于平衡纵向数据，考虑线性模型：其中，β=β1，β2，…，βp

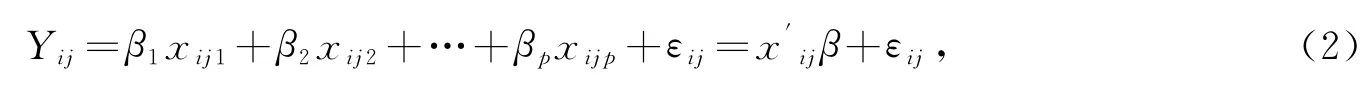
（）′是一个p维向量，表示待估计的回归系数，εij为随机误差项，表示响应变量与x′β的偏差.不失一般性，对于任意的i和j，令xij1=1，即β1为线性模型中的截距项.利用矩阵描述，其第i个回归方程有下面的形式：

2.2EN方法

Elastic Net，又称弹性网技术，它是在Lasso的基础上，通过引入系数的二次惩罚项而得到的［5］，它比Lasso方法［6，11］更能有效的处理高维小样本数据的方法.

假设数据的样本量为n，预测变量个数为p，响应变量y=y1，…，y n（

）T，预测变量xj=，X是由p个预测变量组成的矩阵，首先对响应变量和预测变量分别进行中心化处理和标准化处理.

对于普通线性模型，EN方法定义如下：

3　EN方法在平衡纵向数据模型中的应用

3.1平衡纵向数据EN估计的方法

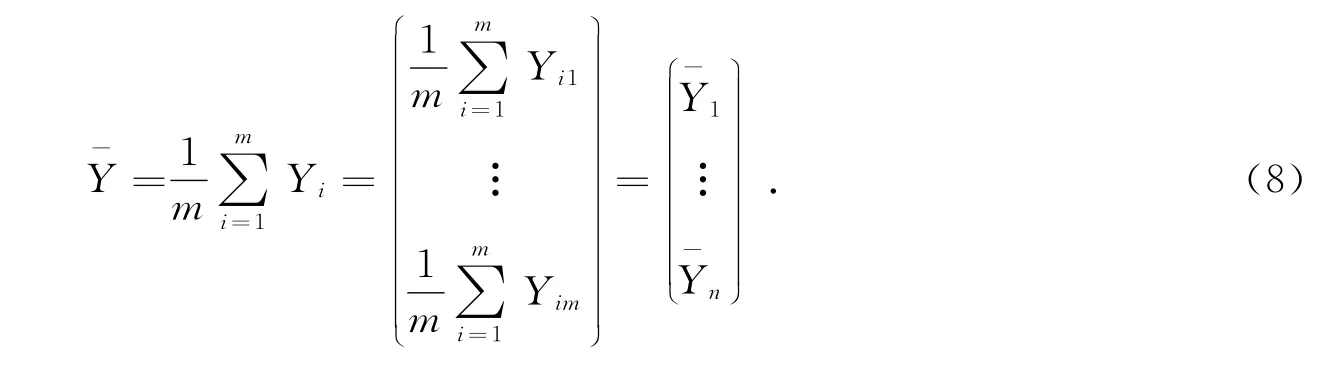
通过对每个实验个体的重复观测，可以获得相应变量Yi和预测变量Xi，i=1，…，m.利用极大似然函数估计方法来估计系数，其极大似然函数定义如下：

对上式取e为底的对数，得到似然函数［8］：

参数β的估计为：

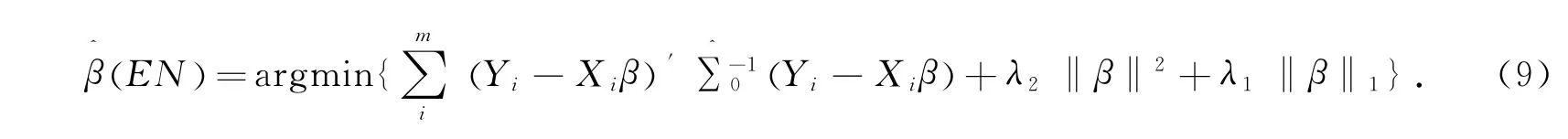
3.2平衡纵向数据模型EN估计的性质

EN估计具有组效应性质［6.7］，对于强相关变量组的数据，能将其全部选入模型而不是只选择一个，弥补了Lasso方法只能选择变量组中的一个变量的不足.现研究在平衡纵向数据模型下，EN估计的组效应性质.

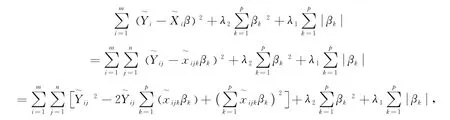
所以

同理，

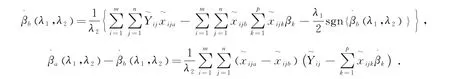
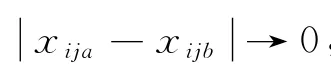
定理1从理论上揭示了平衡纵向数据模型的EN估计具有组效应性质，对于具有强相关性的变量，EN估计能将强相关变量全部选入模型，而并非只选择其中一个，且系数估计的差距随着相关系数的增大而减小.

3.3数值模拟

现通过数值模拟加以验证EN方法在处理具有强相关变量组的数据上更具有有效性.由于EN方法的解经转换后可表达为Lasso方法的解的形式，故可以利用最下角回归算法解决其算法问题.结合Lars算法［12］，在R软件［9，10］中进行变量筛选.应用R软件产生m组平衡纵向数据，Xi的每一列都是独立同分布于Nn×10，I（），随机误差εi=εi1，εi2，…，εin（

）′～Nn×10，Σ（）.对于任意给定的β=β1，β2，…，βp（

）′，应用线形模型Yi=Xiβ+εi，可以获得Y= Y1，Y2，…，Ym（）′.这里用来仿真模拟的平衡纵向数据形式如（1）式所示.现假设在模型中的变量关系如下：

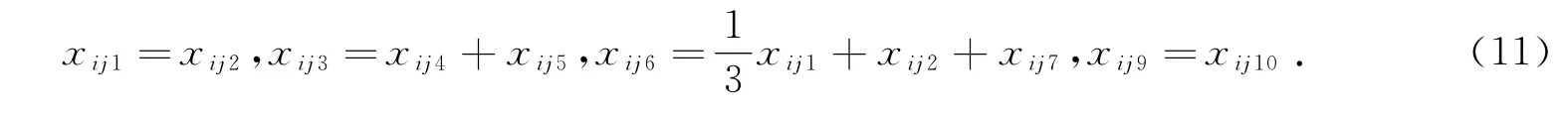
表1　数值模拟得到的系数估计值

由表1可知：两种方法均可以准确估计出参数值，如xij4真实值为1，EN方法和Lasso方法估计的参数值分别为0.9994和1.但在变量强相关条件下，两种方法结果不同.例如：对于存在强相关的变量组xij1与xij2，EN 方法把xij1与xij2都选入了模型，而Lasso方法只选择了变量xij1；同样，对于强相关变量xij9和xij10，EN方法把xij9与xij10都选入了模型，而Lasso方法只选择了变量xij9；这是由于EN方法具有组效应性质.同时这也表明，对于数据中存在强相关变量组的情形，运用EN方法选择出的变量更接近于真实模型.

综上，在将平衡纵向数据模型与EN方法结合后，EN方法仍然在处理具有强相关变量组的数据上显著优于Lasso方法.

4　结论

本文鉴于EN方法能有效处理强相关数据的事实，将EN方法运用于纵向数据模型中，证明纵向数据模型的EN估计具有组效应性质，并通过数值模拟验证了EN方法能将强相关变量全部选入纵向数据模型而Lasso方法并没有这方面的作用.

综上可知，EN方法能有效克服传统纵向数据参数估计方法的不足，使纵向数据变量估计的拟合效果和预测能力得到改善.

［1］BREIMAN L.Heuristics of instability and stabilization in model selection［J］.Ann Statist，1996，24（6）：2350-2383.

［2］FAN Jian-qing，LI Run-ze.Variable selection via nonconcave penalized likelihood and its oracle propertrices［J］.Journal of the American Statistical Association，2001，96：1348-1360.

［3］A.E.Hoerl，R.W.Kennard.（1970）Ridge regression：biased setimation for nonorthogonal probled.Technometrics 12（1）：55-67.

［4］TIBSHIRANI R.Regression shrinkage and selection via the Lasso［J］.Journal of the Royal Statistical Society，Series B，1996，58：267-288.

［5］Zou H，HASTIE T.Regularization and Variable Selection via the Elastic Net［J］.Journal of the Royal Statistical Society，Series B.2055，67（1）：301-320.

［6］TIBSHITANI R.Regression Shrinkage and Selection via the Lasso［J］.Journal of the Royal Statistical Society，Series B，1996，58：267-288.

［7］卢颖.广义线性模型基于Elastic Net的变量选择方法研究［D］.北京：北京交通大学，2001.

［8］李春红，韦新星.Elastic Net方法在COX模型变量选择中的研究［J］.重庆：西南大学学报，2015.

［9］吴喜之.复杂数据统计方法——基于R的应用［M］.北京：中国人民大学出版社，2010.

［10］薛毅，陈立萍.R语言实用教程［M］.北京：清华大学出版社，2014.

［11］曲婷，王静.基于Lasso方法的平衡纵向数据模型变量选择［J］.哈尔滨：黑龙江大学自然科学学报：2012.

［12］Efron B，Hastie T，Johnstone I，et al.Least Angle Regression Model［J］.Biometrika，1982，69（1）：239

-241.

Application of Elastic Net Method in Balanced Longitudinal Data Models

Xu Liqing1Tian Kai1Xiong Qin2
（1.Guang Xi University，Academy of Mathematics and Information Sciences，Nan Ning 530004，China；2.Guangxi University of Science Technology，Medical College，Liu Zhou 545006，China）

We apply the Elastic Net method to select variables so as to establish the corresponding longitudinal data model.It is found that the Elastic Net method possesses a group effect property.The numerical simulations on the Elastic Net method and the Lasso method show that the former is superior to the latter in dealing with strong correlated variables in longitudinal data models.

Elastic Net method Longitudinal data model Model selection Group effect property

国家自然科学基金（71462002）和广西自然科学基金（2013GXNSFAA019340）资助

2016年01月14日