具有给定围长单圈图的 Harary指数的最大值*

陈单单

（湖南财经工业职业技术学院公共课部，湖南，衡阳，421002）

具有给定围长单圈图的Harary指数的最大值*

陈单单

（湖南财经工业职业技术学院公共课部，湖南，衡阳，421002）

本文首先给出了单圈图的Harary指数的一种计算方法，然后利用这一方法给出了具有给定围长单圈图的Harary指数的最大值，以及对应的极图.

围长 单圈图 Harary指数 反距离

1　引言

拓扑指数是从化合物的结构图衍生出来的一种数学不变量.大约在一百多年之前就引入了拓扑指数，至今已有200多种被证实在结构-活性/性质相关性（QSAR/QSPR）中非常有用，这些指数中有些是基于图中点的距离，有些是基于图中点的度数.而Harary指数是基于图中点的距离.

在1993年，PlavšiC等［1］和Ivanciuc等［2］各自独立提出了Harary指数模型来刻划分子结构图.设G=（V，E）是一个简单的连通图，其中V和E分别为G的顶点集和边集，则图G的Harary指数定义为

Diudea［3］对路、圈、星图的Harary指数进行了计算，给出了一些有意义的结论，并通过对这些图的Harary指数可达或不可达值的分析，得出Harary指数对刻画分子结构图意义十分重大.Harary指数与Wiener指数都是基于图中点的距离，由于在许多情况下，原子之间距离较远的影响小于与其相邻的原子，在描述分子结构图时，Harary指数优于Wiener指数［4］，并使分子的结构属性得到改善［5］.有关Harary指数有许多有趣的属性，以及与其它距离拓扑指数的关系见［6-15］.

本文首先给出了单圈图的Harary指数的一种计算方法，然后利用这一方法给出了给定围长单圈图的Harary指数的最大值，以及对应的极图.

2　单圈图的Harary指数的计算

本文所涉及的图都是连通的简单无向图.设G=（V，E）是顶点集和边集分别是V和E的图，G 的顶点数用n（G）表示，称为G 的阶.顶点u与v之间的距离dG（u，v）（或d（u，v））是指G中连接顶点u与v之间的最短路径的长度.图G的Harary指数定义为

若G=（V，E）是一个n阶单圈图，其中的圈Cm=v1v2…vmv1的长度为m （即围长）且m≤n ，则G-E（Cm）的连通分支Ti（i=1，2，…，m）都是树，Ti与Cm的公共顶点为vi，这样的单圈图我们用G=U（Cm；T1，T2，…，Tm）表示.令n（Ti）=li+1，则l=l1+l2+…+lm= n-m.特别地，若Ti=Sli+1是以vi为中心的li+1阶星图，则G=U（Cm；T1，T2，…，Tm）= U（Cm；Sl1+1，Sl2+1，…，Slm+1）；若Ti=Pli+1是以vi为其中一个端点的li+1阶路，则G= U （Cm；T1，T2，…，Tm）=U （Cm；Pl1+1，Pl2+1，…，Plm+1）.

为了计算n阶单圈图G的Harary指数，我们需要了解有关树的Harary指数的结果.

引理1［15］ 设T是任意不同于星图Sn与路Pn的n阶树，则

关于圈的Harary指数，我们很容易证明下面的结论：

引理2 设Cn是n阶单圈图，则

下面我们给出关于单圈图Harary指数的一个计算方法.

定理3 设G=U（Cm；T1，T2，…，Tm）是一个n阶单圈图，则

证明 我们将图G的顶点之间的反距离分为四类：（i）两个顶点都在圈Cm上；（ii）两个顶点中一个在圈Cm上，另一个在某Ti-｛vi｝上；（iii）两个顶点都在同一个Ti-｛vi｝上；（iv）两个顶点中一个在Ti-｛vi｝，另一个在Tj-｛vj｝上（i≠j）.

（i）设两个顶点都在圈Cm上的反距离之和为H1，则

（ii）设两个顶点中一个在圈Cm上，另一个在某Ti-｛vi｝上的反距离之和为H2，则

（iii）设两个顶点都在同一个Ti-｛vi｝，i=1，2，…，m上的反距离之和为H3，则

（iv）设两个顶点中一个在Ti-｛vi｝，另一个在Tj-｛vj｝，（i≠j）的反距离之和为H4.∀x∈Ti-｛vi｝，∀y∈Tj-｛vj｝，则

于是，Ti-｛vi｝与Tj-｛vj｝中顶点之间的反距离之和为

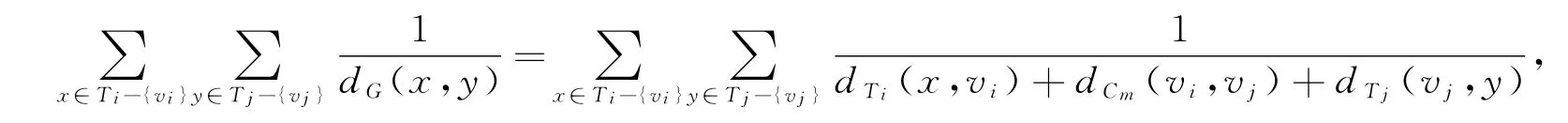
因此，

从而

3　给定围长的单圈图的最大Harary指数

这一节我们首先给出具有给定围长m（3≤m≤n）的单圈图的Harary指数的界，然后刻划出具有给定围长的单圈图G中具有最大Harary指数的图的特征.

定理4 设G=U（Cm；T1，T2，…，Tm）是一个n阶单圈图，Ti是li+1阶的树，i=1，2，…，m，则有

H （U （Cm；Pl1+1，Pl2+1，…，Plm+1））≤H （G ）≤H （U （Cm；Sl1+1，Sl2+1，…，Slm+1））.

左等号成立当且仅当G≅U（Cm；Pl1+1，Pl2+1，…，Plm+1），而右等号成立当且仅当G≅U （Cm；Sl1+1，Sl2+1，…，Slm+1）.

证明 由引理1知，H （Pli+1）≤H （Ti）≤H （Sli+1）且左等号成立当且仅当Ti≅Pli+1，vi是Pli+1的一个端点；右等号成立当且仅当Ti≅Sli+1，vi是Sli+1的中心，i=1，2，…，m.设V（Ti）-｛vi｝=V（Sli+1）-｛vi｝=｛y1，y2，…，yli｝，Pli+1=viy1y2…yli.不妨设在Ti中y1，y2，…，yli到vi的距离是不减的，即dTi（vi，y1）≤dTi（vi，y2）≤…≤dTi（vi，yli），则

因为

而

因此，对于x ∈Cm，有

和

同样地，有

由定理3得

H（U （Cm；Pl1+1，Pl2+1，…，Plm+1））≤H（G ）≤H（U （Cm；Sl1+1，Sl2+1，…，Slm+1）），

左等号成立当且仅当G≅U（Cm；Pl1+1，Pl2+1，…，Plm+1）；右等号成立当且仅当G≅U（Cm；Sl1+1，Sl2+1，…，Slm+1）.

由上述结论，我们现在可以给出具有给定围长的单圈图中具有最大Harary指数的特征.

定理5 设G=U（Cm；T1，T2，…，Tm）是任意一个围长为m单圈图，则

等号成立当且仅当G≅U（Cm；Sn-m+1，S1，…，S1），即U（Cm；Sn-m+1，S1，…，S1）是围长为m的n阶单圈图中唯一具有最大Harary指数的图.

证明 由定理4

下面证明：

因此，H（U（Cm；Sn-m+1，S1，…，S1））≥H（G）等号成立当且仅当l2=0，即

利用定理3，我们可计算出两个围长分别m和m-1为的n阶单圈图U（Cm；Sn-m+1，S1，…，S1）和U（Cm-1；Sn-m+2，S1，…，S1）的Harary指数，直接比较可得n 阶单圈图的Harary指数的最大值.

［1］PlavsiC，D.&S.NikoliC&N.TrinajstiC&Z.MihaliC.On the Harary index for the characterization of chemical graphs［J］.J.Math.Chem.1993，（12）：235-250.

［2］Ivanciuc，O.&T.S.Balaban&A.T.Balaban.Reciprocal distance matrix，related local vertex invariants and topological indices［J］.J.Math.Chem.1993，（12）：309-318.

［3］Diudea，M.V.Indices of reciprocal properties or Harary indices［J］.J.Chem.Inf.Comput.Sci.1997，（37）：292-299.

［4］Lucic，B.&A.Milicevic&S.Nikolic&N.Trinajstic.Harary index-twelve years later［J］.Croat.Chem. Acta，2002，（75）：847-868.

［5］Trinajstic，N.&S.Nikolic&S.C.Basak&I.Lukovits.Distance indices and the their hyper-counterparts：Intercorrelation and use in the structure-property modeling［J］.SAR QSAR Environ.Res.2001，（12）：31-54.

［6］Ivanciuc，O.&T.Ivanciuc&A.T.Balaban.Design of topological indices.Part 10.Parameters based on electronegativity and vovalent radius for computation of molecular graph descriptors for heteroatom-containing molecules［J］.J.Chem.Inf.Comput.Sci.1998，（38）：395-401.

［7］Zhou，B.&X.Cai&N.Trinajstic.On Harary index［J］.J.Math.Chem.2008，（44）：611-618.

［8］Das，K.Ch.&B.Zhou&N.Trinajstic.Bounds on Harary index［J］，J.Math.Chem.2009，46：1369 -1376.

［9］Zhou，B.&Z.Du&N.Trinajstic.Harary index of landscape graphs［J］.Int.J.Chem.Model.2008，（1）：35-44.

［10］Gutman，I.A property of the Wiener number and its modifications［J］.Indian J.Chem.1997，（36A）：128-132.

［11］Zhou，B.&I.Gutman.Relationships between Wiener，hyper-Wiener and Zagreb indices［J］.Chem. Phys.Lett.2004，（394）：93-95.

［12］Zhou，B.&N.Trinajstic.On the maximum eigenvalues of the reciprocal distance matrix and the reverse Wiener matrix［J］.Int.J.Quantum Chem.2008，（108）：858-864.

［13］Ivanciuc，O.&T.S.Balaban&A.T.Balaban.Reciprocal distance matrix，related local vertex invariants and topological indices［J］.J.Math.Chem.1993，（12）：309-318.

［14］Das，K.C.&K.Xu&I.N.Cangul&A.S.Cevik&A.Graovac，On the Harary index of graph operations［J］.Journal of Inequalities and Applications.2013，2013：339.

［15］Xu，K.&K.H.DAS.Extremal unicyclic and bicyclic graphs with respect to Harary index［J］.Bull.Ma

lays.Math.Sci.Soc.2013，36（2）：373-383.

The Maximum Value for the Harary Index of Unicyclic Graphs with a Given Girth

Chen Dandan
（Department of Public Course，Hunan Financial&Industrial Vocational-Technical College，Hengyang 421002，China）

In this paper，we first give a formula for calculating the Harary index of a unicyclic graph according to the structure，and then using this formula，we obtain the maximum value for the Harary index of unicyclic graphs with a given girth，and characterize the extremal graph with respect to the Harary index.

Girth Unicyclic graph Harary index Reciprocal distance

2016年05月09日