平原河道桥墩阻水比与壅水特性关系

王玲玲,张凤山,唐洪武

(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京　210098;2.河海大学水利水电学院,江苏 南京　210098)



平原河道桥墩阻水比与壅水特性关系

王玲玲1,2,张凤山1,2,唐洪武1,2

(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京210098;2.河海大学水利水电学院,江苏 南京210098)

针对平原地区河道桥墩壅水问题,采用数值模拟方法,以阻水比α为控制参数,按照产生机制和影响范围的不同,从墩前冲高和桥前壅高两方面考虑桥墩壅水效应。墩前冲高的影响范围由河道断面水位壅高变异系数确定,在高阻水比(α>7%)情况下,其影响范围相对集中在桥墩附近;对于桥前壅高,以防洪工程中起重要作用的断面平均壅高为表征变量,分析无量纲的相对壅高βyg及最大壅高点距桥墩的相对距离λyg与阻水比之间的关系。结果表明:在高阻水比时,最大壅高位置出现在墩前4～5倍墩宽处,且阻水比的增加会导致桥前最大壅高迅速增大和壅水影响范围的持续扩大;阻水比7%是平原河道桥前水位壅高特性的重要分界点,故大中型桥梁工程的阻水比以不大于7%为宜。

平原河道;桥墩壅水;阻水比;数值模拟；墩前冲高；桥前壅高

桥墩的束窄作用使得桥址处河道过水断面减小,在流量一定的条件下,会引起局部水位壅高,尤其是平原河道的桥梁,桥前壅水现象更为明显,壅水影响范围更大。为规范涉河工程的防洪评价,2004年水利部组织制订了《河道管理范围内建设项目防洪评价报告编制导则(试行)》,明确了壅水影响是涉水工程防洪评价的重要评价因子之一,提出壅水影响可采用经验公式法计算。目前工程中最常用的经验公式是JTJ 062—1991《公路桥位勘测设计规范》[1](以下简称《规范》)中的推荐公式。该公式应用简单方便,但应用于平原河网地区时,不仅壅水的物理概念模糊,计算的“壅高值”含义和位置特性无清晰界定,其量值与理论及试验结果也常有较大差距,表现为壅高值及其影响范围显著偏小[2],现有理论成果及工程应用中,对墩柱阻水比的控制阈值也无量化指标。因此,涉水工程墩柱壅水特性方面还有大量问题有待深入系统地研究。

桥墩壅水问题是一个传统的水力学问题,国内外学者通过经验公式[3-6]、物理模型[7-8]和数值模拟[9-16]等方法,对桥墩壅水效应进行了大量研究。其中,经验公式法用以粗略求解桥前壅水值以及壅水影响范围，如王开等[5]结合水工模型试验资料,对比检验了不同形式桥墩的壅水计算公式,提出了各经验公式的适用范围;夏丽丽等[6]利用水面曲线法推求桥墩壅水值,结果表明公式中选取上游渐变流断面的位置对壅高结果有很大影响。经验公式法虽然计算简便,但只能用以估算断面平均壅水值,精度较低,适用范围小[9]。与经验公式法相比,物理模型虽能直观地模拟墩前壅水形态,但费时耗物且成果难以通用,现阶段数值模拟方法得到越来越多的应用,如邓显羽等[10]和刘正风等[11]运用HEC-RES模型分别模拟了不同洪水频率下桥梁壅水高度、壅水长度以及多桥梁连续阻水下的壅水曲线,达到了较高精度;Seckin等[12]、Cobaner等[13]通过人工神经网络对桥墩周围的流场分布以及桥墩冲刷进行了模拟;解鸣晓等[14]建立二维数值水槽模型,探讨了壅水值对糙率及紊动黏性系数的敏感性,结果显示壅水值随糙率变化不大,但对紊动黏性系数的变化较为敏感;林忠灯等[15]采用有限体积法的思想建立三维模型,引用通量差分分裂算法求解控制方程,较好地模拟了桥墩周围的水流现象。相对而言,数值模拟方法具有成熟的理论体系,但现有研究少有针对平原河网区平底河道条件下的桥墩壅水规律及其对上、下游两岸防洪工程的影响而开展。本文针对平原地区平底河道开展桥墩壅水规律研究,明确墩前最大壅高的位置,揭示阻水比与最大壅高的定量关系,成果可为涉水工程防洪评价及其导则修编提供参考。

1　模 型 建 立

1.1依托工程简介

图1　河道断面示意图 (单位:m)Fig. 1　Sketch of cross-section of river (units: m)

采用里下河地区某流域性河道的断面尺寸及水力要素作为参照建立模型,该河道是一条以引水为主,具有灌溉、排涝、航运、生态旅游综合作用,双向运行的平底人工河道,水面比降极小,流速低缓,断面形状为梯形且沿程保持不变,如图1所示。该河道护坡完整、河势稳定,河床冲淤现象微弱。

1.2模型概况

1.2.1计算区域及桥墩布置

以跨越该人工河道的某省道桥梁的桥墩为对象进行算例设计。计算区域河段长度取5 km,桥址上、下游分别为3 km、2 km。跨河桥梁采用双桥墩对称布置,矩形桥墩长宽比2.5∶1,顺流向布置,桥墩与堤脚最近距离为8.1 m。控制阻水比α在2%～9%范围内,共设8个研究工况,α分别设为2%、3%、4%、5%、6%、7%、8%、9%,对应的桥墩断面尺寸依次为1.9 m×4.76 m、2.87 m×7.18 m、3.8 m×9.5 m、4.76 m×11.9 m、5.71 m×14.28 m、6.66 m×16.65 m、7.61 m×19.04 m、8.57 m×21.42 m。

1.2.2定解问题及网格划分

建立平面二维水动力数学模型,圣维南方程可简化为以下控制方程组[9]:

(1)

式中:Z——水位;H——水深;U、V——x、y方向水深平均流速;g——重力加速度;C——谢才系数;νt——紊动黏性系数。

图2　桥墩附近网格(α=7%)Fig. 2　Grids near piers (α=7%)

运用交错网格有限差分法离散控制方程组,ADI算法求解流速和水位,离散方程的求解采用追赶法[17]。根据该河道的实际运行条件,边界条件取为:上游流量为300 m3/s,下游水位为1.51 m,河道糙率为0.021,时间步长为0.02 min,计算时长为24 h。各参数的组合可以满足计算收敛与稳定要求。采用矩形网格剖分计算区域。网格在桥墩附近渐变加密,最小空间步长在0.95～2.3 m之间,调整桥墩附近的网格尺度使之精确模拟各工况矩形桥墩的实际阻水面积及阻水特性。以α=7%为例,整个计算区域网格数量为516×54,如图2所示。

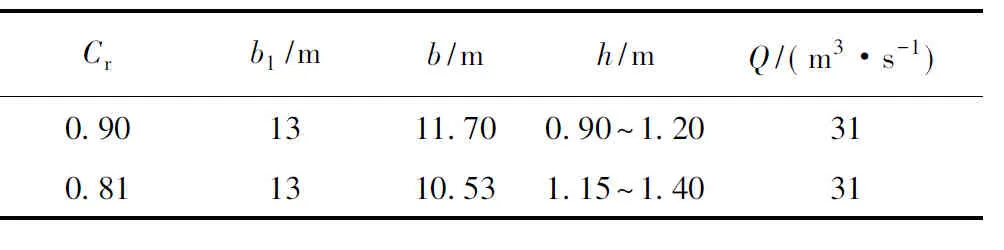
表1　El-Alfy试验主要控制参数Table 1　Control parameters of El-Alfy’s experiment

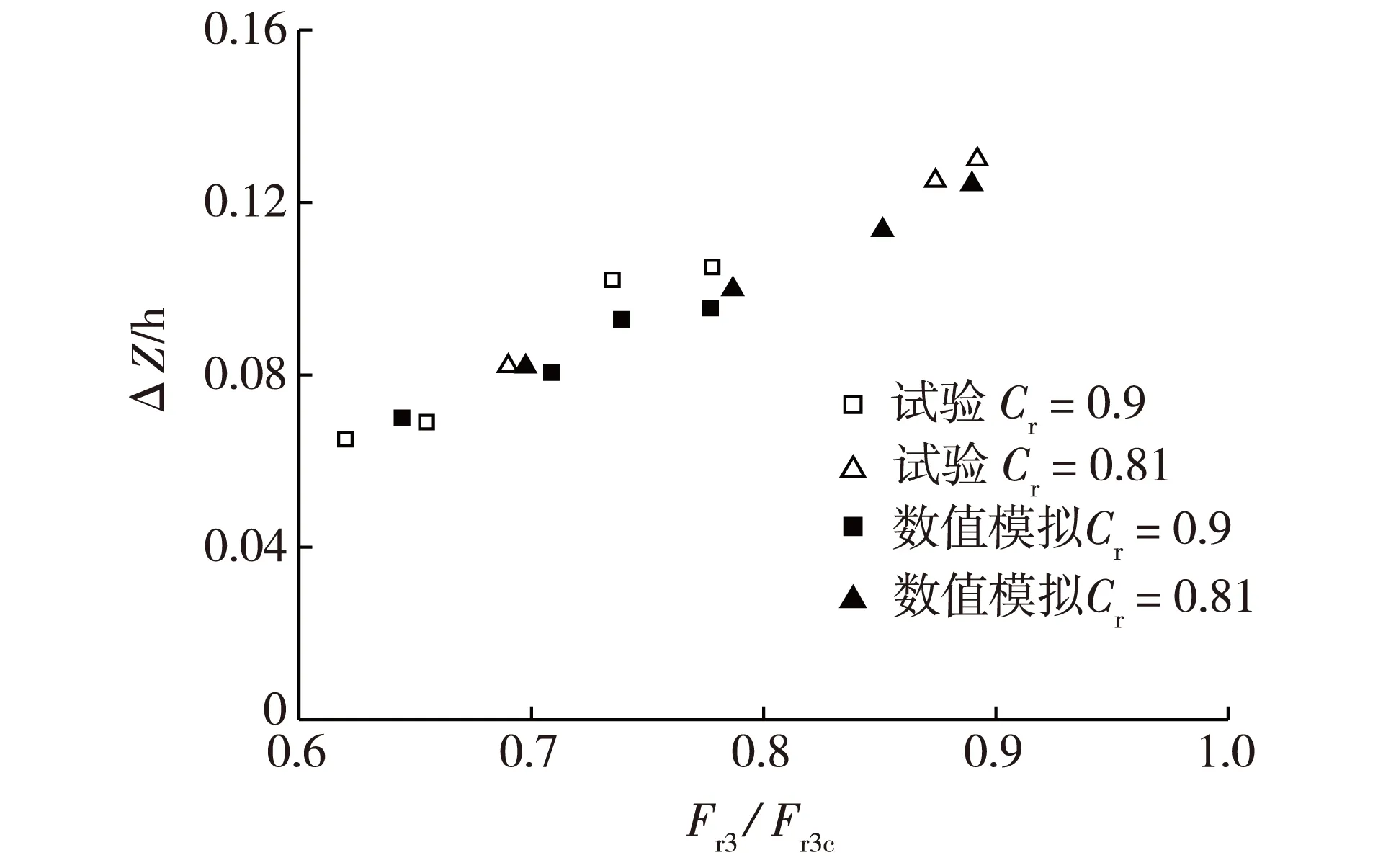
图3　壅高值验证Fig. 3　Comparison of calculated and measured backwater heights

2　模 型 验 证

采用El-Alfy[18]的试验成果验证模型,试验水槽为

矩形断面,矩形双桥墩对称布置,试验工况及主要控制参数见表1。表1中b1为水槽宽度,b为过流宽度,收缩系数Cr=b/b1,h为下游水深(取桥墩下游水面线与天然水面重合处的水深),墩间距为b/3,Q为上游进口流量。

图3为不同收缩系数时水槽中心线纵断面桥墩上游最大壅高ΔZ计算结果与El-Alfy试验结果比较。图3中,Fr3为下游断面(水面线与天然水面重合处的断面)Froude数;Fr3c为下游临界Froude数,由式(2)[18]确定:

(2)

式中:r——桥墩下游断面和上游断面(最大壅高断面)的能量残值比,取r=0.95(根据文献[18],r=0.9～1.0)。

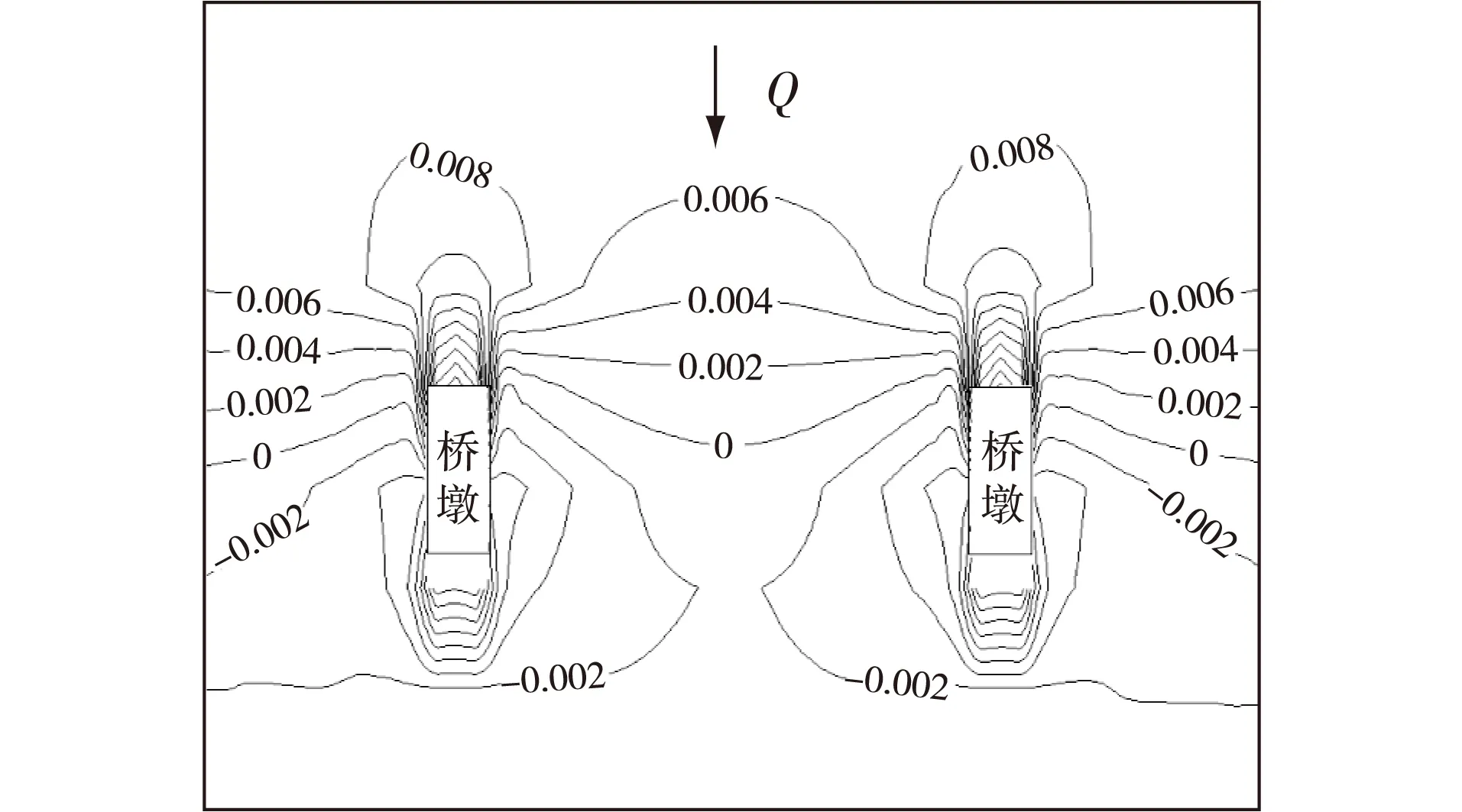
图4　桥墩附近水位壅高等值线(α=7%，单位：m)Fig. 4　Contours of backwater height near piers(α=7%, units: m)

根据文献[18],壅高值的定义是水槽中心线纵断面桥墩上游最大壅高。由图3可知,壅高的计算结果与试验结果吻合良好,误差在5%以内，表明该数学模型对于桥墩壅水计算具有较高精度,可用于桥墩壅水特性研究。

3　平原河流桥墩壅水规律模拟

3.1墩周壅水分布规律

在桥墩壅水问题研究中,常涉及墩前冲高与桥前壅高2个概念。图4为α=7%工况桥墩附近水位壅高等值线,该图显示墩周壅水具有以下特点:

a. 沿河道中心线、墩中心线和近岸顺流向的水面线分布呈不同的变化规律。墩前水位急剧冲高,最大冲高值高达2.68 cm,但影响范围极小,顺流向仅约1倍墩长,垂直流向不足2倍墩宽;河道中心以及近岸水位壅高相对较平缓,但影响范围为河道全断面。

b. 桥墩中心上游侧水位壅高,下游水位跌落。壅水范围远大于跌水范围,壅高的断面平均幅值也数倍于墩下游水位跌水幅值。

对于距离岸边界2倍墩宽以上的桥墩,墩前冲高的影响范围很有限,此时墩前冲高对河岸堤防高程设计无显著影响;而对于紧靠岸坡布置的桥墩,由于墩前流速明显小于河道中心处,墩前冲高虽可能对堤防设计有影响,但通常影响仍然不大。

对于影响范围达到河道全断面的桥前壅高,在平原地区河道中,理论上该壅高值可能波及桥址上游非常大的范围。桥前壅高对于桥址上游两岸的防洪工程影响重大,尤其是多工程迭加情况下,桥墩上游的水位壅高更是直接关系到河道堤防高程的确定[11]。

算例中天然状态下的水面比降约为3.8×10-5,以阻水比为7%工况为例,有规范公式[1]:

(3)

(4)

计算得ΔZ=0.68 cm,L=351 m,而数值模拟结果表明距桥墩上游3 km外上游边界处的河道中心点壅水值仍有0.6 cm,壅水影响远未消减为零,可见两者在壅水影响范围的计算上相差甚远。

3.2桥墩阻水比对墩前冲高的影响

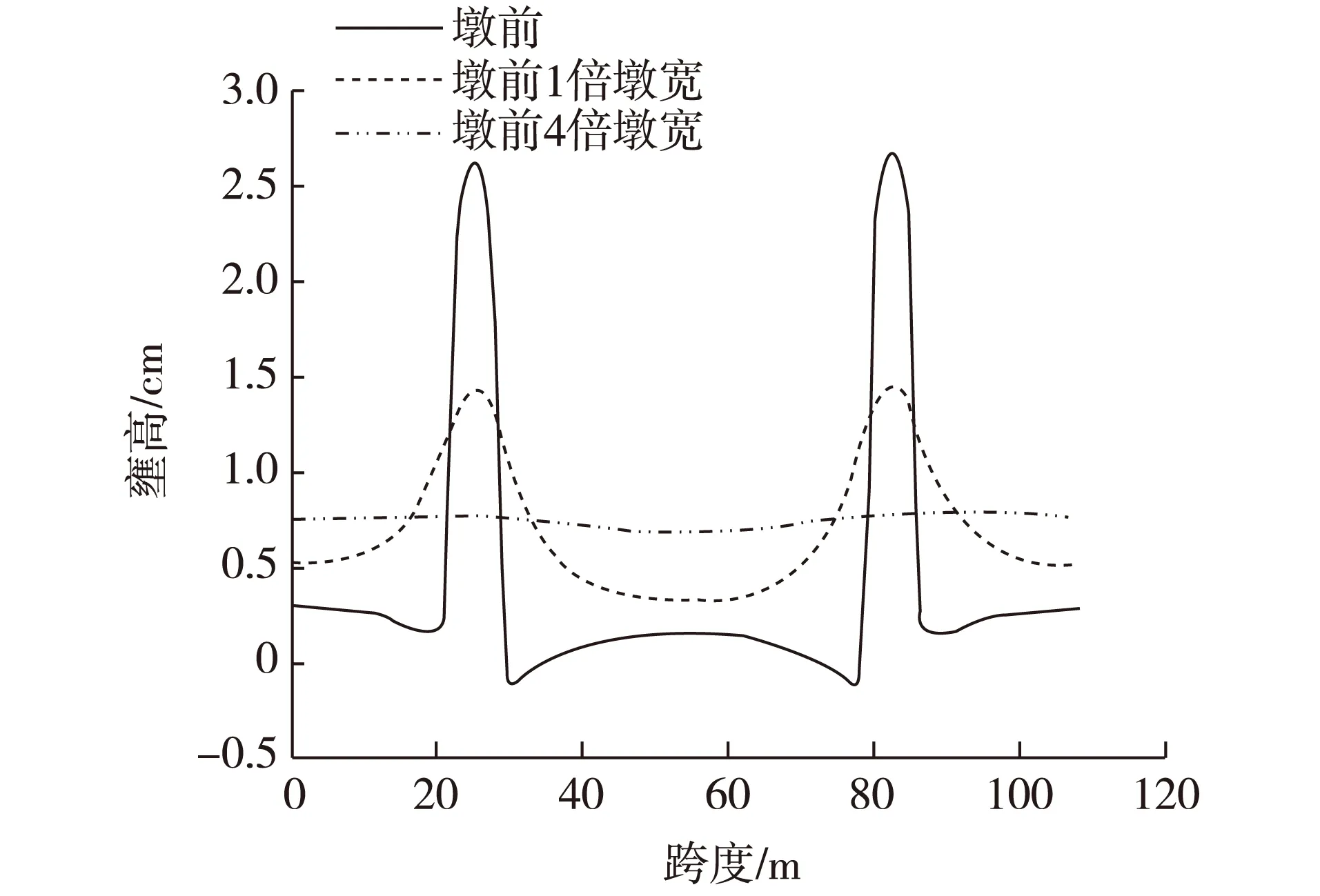
图5　墩前各断面水位壅高分布(α=7%)Fig. 5　 Distribution of backwater height in every section in front of pier (α=7%)

相关规范[1]在确定堤防高程时,认为桥址附近的水位壅高值从墩前到两岸呈线性规律变化,斜率近似取桥位河段顺流向天然水面坡降[15]。但在实际情况中,由于墩前冲高的影响,桥址附近的水位壅高值分布较为复杂。以阻水比7%为例,图5给出了墩前断面以及墩前1倍墩宽和4倍墩宽断面内壅高值的分布规律。由图5可知,在墩前4倍墩宽断面处水面已平坦,可认为此处的墩前冲高影响已消失。

为了确定不同阻水比时墩前冲高的影响范围,以同一断面内各计算节点水位壅高值的变异系数(CV=标准差/平均值)作为判断墩前冲高影响程度的标准。当CV> 5%时表明该横断面内水位分布不均,冲高影响明显,反之CV≤ 5%时则表明墩前冲高影响范围结束。表2给出了不同阻水比情况下,变异系数小于5%的临界断面与桥墩的距离Lcg以及该距离与墩宽B比值的无量纲参数λcg,表中同时给出了墩前绝对冲高值Hcg、相对冲高βcg(βcg=Hcg/B)以及临界断面与桥墩之间顺流向的最小及最大网格尺度Lgmin、Lgmax。

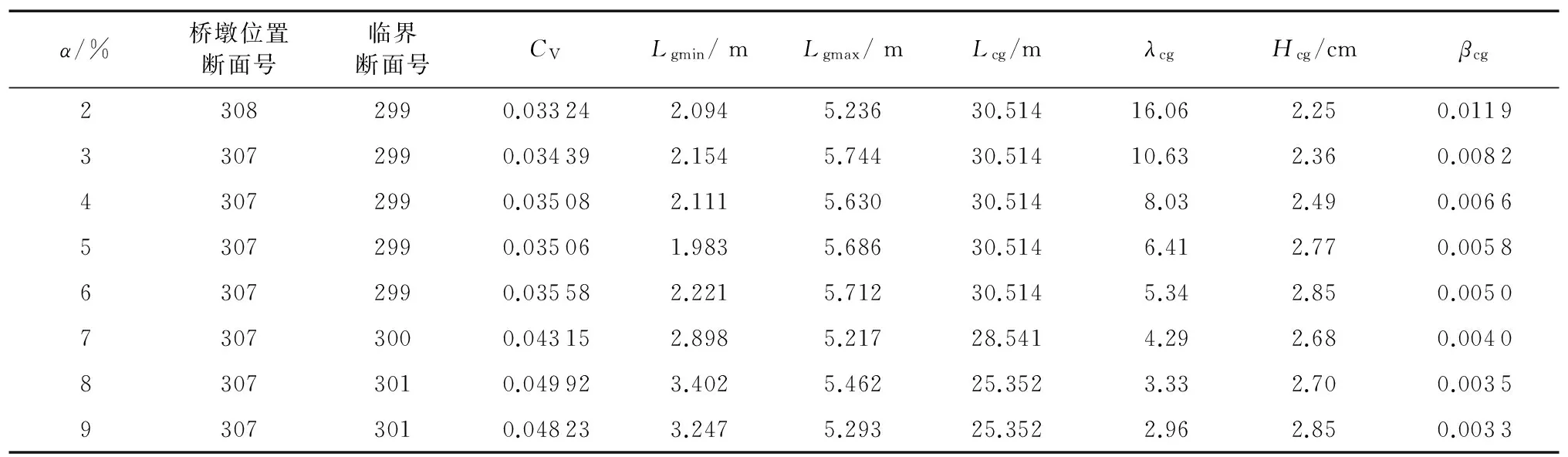
表2　各阻水比情况下墩前冲高的影响Table 2　Influence area of creep height in front of piers in every water-blocking ratio condition

如图6所示,随着阻水比的增大,临界断面距墩前的距离基本保持在30 m以内,且有减小趋势。同时,用来表示冲高范围的相对距离λcg逐渐减小,但阻水比为4%和7%时存在2个明显的拐点,在拐点之间,λcg与阻水比大致呈3段线性变化。当阻水比较小(α<4%)时,λcg随阻水比的增大迅速减小;当阻水比较大(α>7%)时,λcg随阻水比增大缓慢减小,且保持在较低数值。表明高阻水比情况下墩前冲高的影响范围更集中在桥墩附近,影响范围相对较小。

虽然随着阻水比的增加,墩前冲高的绝对值有缓慢增加的趋势,但无量纲的相对冲高βcg和阻水比之间同样存在分段递减的关系,并以阻水比4%和7%为拐点,如图7所示。表明相较于低阻水比情况,在阻水比较高时墩前冲高的相对值没有明显朝不利的方向发展。

图6　冲高影响相对距离λcg与阻水比α的关系Fig. 6　Relationship between relative distance λcgrepresenting influence area of creep height and water-blocking ratio α

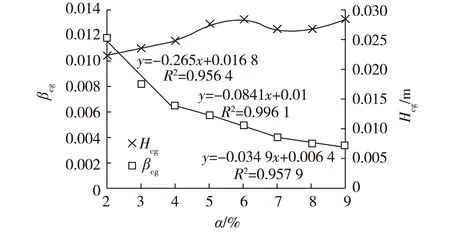
图7　相对冲高βcg与阻水比α的关系Fig. 7　Relationship between relative creep height βcgand water-blocking ratio α

3.3桥墩阻水比对桥前水位壅高的影响

在涉水工程防洪评价中,相较墩前冲高而言,更有意义的指标参数是桥前断面平均壅高,该值关系到桥梁所在河道两岸堤防的安全。图8为不同阻水比情况下断面平均壅高分布,由图8可知,在冲高影响范围以内,断面平均壅高随阻水比的增加有显著增加,且在桥墩上游某一位置处达到最大值后向上游缓慢减小,直至距桥址3 km的上游计算边界处,断面平均壅高只比最大壅高减少了约10%。另外,桥墩下游形成局部跌水,在桥后20 m附近跌水值达到最大,最大跌水值随阻水比的增大而增大,但位置较为固定。桥后跌水的影响范围远小于桥前壅水,在桥址下游200 m内,水面线便与天然水面相重合(水位差小于10-5m)。

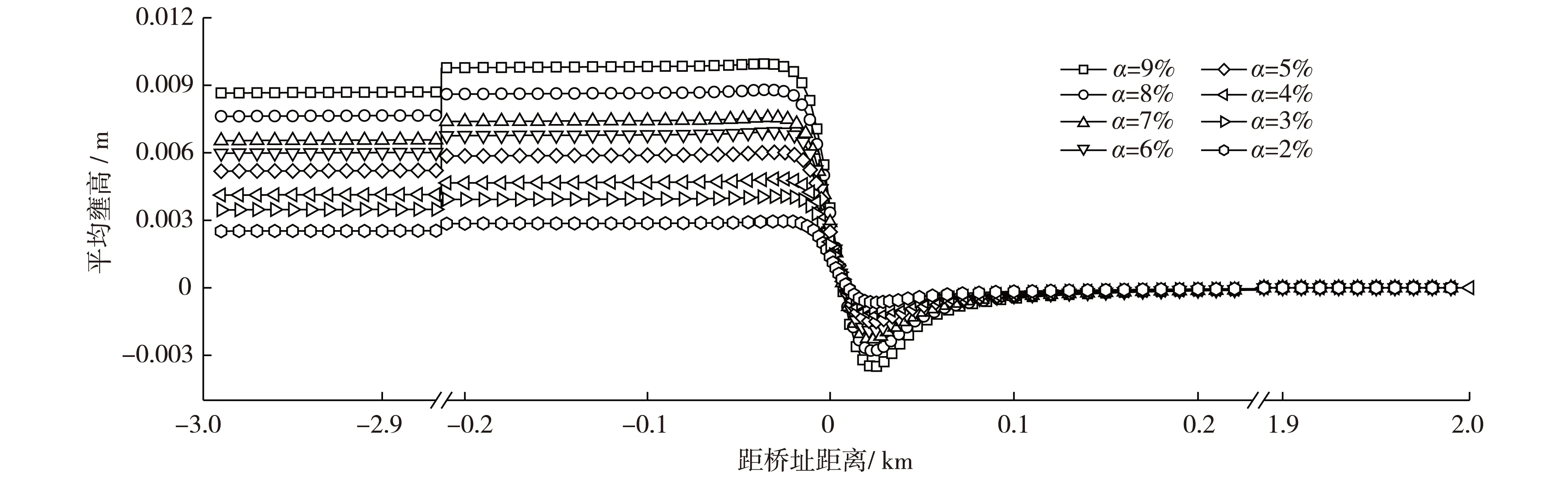
图8　不同阻水比情况下断面平均水位壅高对比Fig. 8　Comparison of cross-sectional average backwater height in different water-blocking ratio conditions

由图9、图10可知,当桥墩阻水比较小时,由于桥墩的阻水面积很小,对水流的影响不明显,壅高值较小,且相对壅高βyg和相对距离λyg(λyg=Lyg/B)均随阻水比的增加迅速以线性规律减小;当阻水比较大(α>7%)时,相对距离λyg缓慢减小并维持在较低的数值,此时壅高最大值位置距墩前断面相对更近,仅为4～5倍墩宽。同时,尽管相对壅高βyg的分母B仍在增加,但βyg却开始增大,表明高阻水比对最大壅高的影响更加强烈。

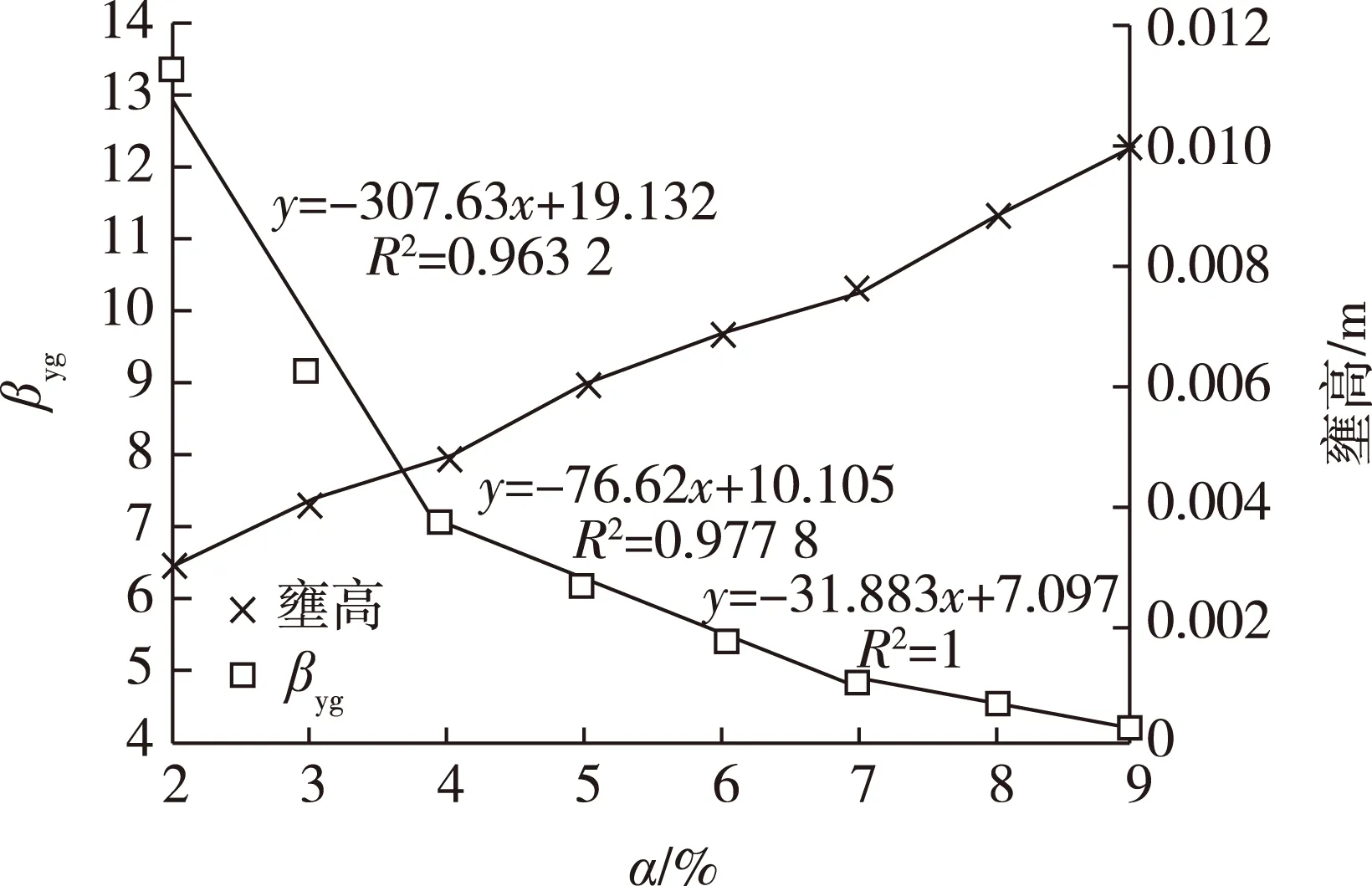
图9　相对壅高βyg与阻水比α的关系Fig. 9　Relationship between relative backwater heightβyg and water-blocking ratio α

图10　桥前最大壅高点距桥墩相对距离λyg与阻水比α的关系Fig. 10　Relationship of relative distance between location with maximum backwater height in front of bridge and pier λyg and water-blocking ratio α

此外,结合图8可知,各阻水比工况下桥前壅水由最大值向上游缓慢消减的比降几乎一致,故壅高值的增大必将导致壅水影响范围的扩大。表明在高阻水比(α>7%)情况下,阻水比的增大会对桥前壅高产生较大的影响,包括壅高值的迅速增大和壅水影响范围的持续扩大。由此可见7%是一个桥前水位壅高特性的拐点。大中型桥梁工程限定其阻水比小于7%具有实际意义。

4　结　　论

a. 桥墩壅水效应可按照形成机制和作用效果分为墩前冲高和桥前壅高。墩前冲高影响范围较小,但关系到桥墩受力与安全稳定。桥前壅高影响范围较大,是涉水工程防洪评价关注的最重要变量之一。

b. 墩前冲高的影响范围顺流向仅约1倍墩长,垂直流向不足2倍墩宽,且随阻水比的增大有减小的趋势。定义墩前冲高影响范围可由断面水位变异系数小于5%的临界断面距墩前断面的相对距离λcg确定,λcg随阻水比的增大而呈分段递减的态势,分段点阻水比分别为4%及7%。在高阻水比(α>7%)的情况下,λcg的变化率较小并维持在较低范围内,表明高阻水比时墩前冲高的影响范围相对更集中在桥墩附近。

c. 桥前最大壅高值随阻水比之间同样存在分段线性关系,分段点阻水比亦为4%和7%。当阻水比较大(α>7%)时,相对距离λyg的梯度进一步减小并维持在较低的数值,而相对壅高βyg却有增大的趋势,此时桥前壅高迅速增大,最大壅高位置出现在墩前4～5倍墩宽处。表明在高阻水比情况下,阻水比的增大会导致壅高值的迅速增大和壅水影响范围的持续扩大。因此,大中型桥梁工程的阻水比以不大于7%为宜。

[1] 交通部公路规划设计院. JTJ 062—1991公路桥位勘测设计规范[S]. 北京:人民交通出版社，1991.

[2] 李付军,张佰战. 桥渡壅水计算[J]. 铁道标准设计,2005(5):43-45. (LI Fujun, ZHANG Baizhan. Computation of bridge crossing choking[J]. Railway Standard Design, 2005(5):43-45. (in Chinese))

[3] BRADLEY J N. Hydraulics of bridge waterways[M]. Washington D C: FHWA, 1978:19-29.

[4] 陆浩,高冬光. 桥梁水力学[M]. 北京:人民交通出版社,1991:54-80.

[5] 王开,傅旭东,王光谦. 桥墩壅水的计算方法比较[J]. 南水北调与水利科技, 2006,4(6):53-55. (WANG Kai, FU Xudong, WANG Guangqian. Comparison of existing backwater models for bridge piers in subcritical flows[J]. South-to-North Water Transfers and Water Science & Technology, 2006, 4(6):53-55. (in Chinese))

[6] 夏丽丽,吴敦银. 防洪评价中跨河桥梁壅水和冲刷计算探讨[J].江西水利科技,2010(4):251-255. (XIA Lili, WU Dunyin. Discussion of the damming height and the erosion depth on the bridge in the flood control assessment[J]. Jiangxi Hydraulic Science & Technology, 2010(4):251-255. (in Chinese))

[7] 季日臣, 何文社, 房振叶. 斜交桥壅水试验研究与理论探讨[J]. 水科学进展, 2007, 18(4):504-508. (JI Richeng, HE Wenshe, FANG Zhenye. Experimental and theoretical study of skew bridge backwater[J]. Advances in Water Science, 2007, 18(4):504-508. (in Chinese))

[8] FENTON J D. Obstacles in streams and their roles as hydraulic structures[C]//Anon.Proceeding 2nd International Junior Researcher and Engineer Workshop on Hydraulic Structures. Pisa, Italy: Edizioni Plus, 2008:15-22.

[9] 陈绪坚, 胡春宏.桥渡壅水平面二维数学模型模拟研究[J].中国水利水电科学研究院学报, 2003, 1(3): 194-199. (CHEN Xujian, HU Chunhong. Research on plenar 2-D mathematical model of bridge pier choked flow[J]. Journal of China Institute of Water Resources and Hydropower Research, 2003, 1(3): 194-199. (in Chinese))

[10] 邓显羽, 李文枫. HEC-RAS模型在密江特大桥防洪评价中的应用[J]. 南水北调与水利科技,2012(1):139-141. (DENG Xianyu, LI Wenfeng. Application of hec-res model for evaluation of flood control of Mijiang Super-long Bridge[J]. South-to-North Water Transfers and Water Science & Technology,2012(1):139-141. (in Chinese))

[11] 刘正风, 占润进, 李文祥. 应用HEC-RAS模型计算连续多桥梁阻水壅高分析[J]. 水利科技, 2011(3):60-61,75. (LIU Zhengfeng, ZHAN Runjin, LI Wenxiang. Analysis of backwater of multi-bridge piers using the HEC-RAS model[J]. Hydraulic Science and Technology, 2011(3):60-61,75. (in Chinese))

[12] SECKIN G, AKOZ M S, COBANER M, et al. Application of ANN techniques for estimating backwater through bridge constrictions in Mississippi River basin[J]. Advances in Engineering Software, 2009, 40(10): 1039-1046.

[13] COBANER M, SECKIN G, KISI O. Initial assessment of bridge backwater using an artificial neural network approach[J]. Canadian Journal of Civil Engineering, 2008, 35(5): 500-510.

[14] 解鸣晓, 张玮. 桩墩影响下的水动力数值模拟[J]. 水利水电科技进展, 2008,28(3):20-24. (XIE Mingxiao, ZHANG Wei. Numerical simulation of open channel flow influenced by pile piers[J]. Advances in Science and Technology of Water Resources, 2008,28(3):20-24. (in Chinese))

[15] 林忠灯, 贾鹏, 胡金星,等. 利用非结构化网格三维模型探讨桥墩周围流动现象[J]. 水利水电技术,2011(10):55-57. (LIN Zhongdeng, JIA Peng, HU Jinxing, et al. 3-D unstructured grid model based study on flow phenomena around piers[J]. Hydraulic Science and Technology, 2011(10):55-57. (in Chinese))

[16] 徐林春, 郑国栋, 黄东,等.桥梁工程阻水比与河道水位关系初探[J].中国农村水利水电, 2011(4):45-49. (XU Linchun, ZHENG Guodong, HUANG Dong, et al. research on the relationship between water resistance ratio and river water level in bridge engineering[J]. China Rural Water and Hydropower, 2011(4):45-49. (in Chinese))

[17] BIJVELDS M D J P. Numerical modelling of estuarine flow over steep topography[D]. Delft: Delft University of Technology, 2001.

[18] EL-ALFY K S. Experimental study of backwater rise due to bridge piers as flow obstructions[C]//Anon.Tenth International Water Technology Conference. Alexandria: IWTC, 2006: 319-336.

Relationship between water-blocking ratio and backwater for bridge piers on plain rivers

WANG Lingling1, 2, ZHANG Fengshan1, 2, TANG Hongwu1, 2

(1.StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China;2.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China)

The backwater caused by bridge piers on plain rivers was numerically simulated using the water-blocking ratio of piers (α) as the control parameter. The backwater effect of piers was investigated in terms of the creep height in front of piers and the backwater height in front of a bridge according to different generation mechanisms and influence areas. The influence area of the creep height in front of piers was determined by the variation coefficient of the cross-sectional backwater height. It is concentrated around the piers with higher water-blocking ratios (α>7%). The relationships between the dimensionless relative backwater heightβyg, the relative distance from the location with the maximum backwater height to the bridge pier, and the water-blocking ratio were analyzed using the cross-sectional average backwater height as the representation variable. The results show that the maximum backwater height occurs at four to five times the pier width in front of the pier with higher water-blocking ratios, and the increase in the water-blocking ratio causes the maximum backwater height in front of the bridge to rapidly increase and the backwater area to continuously enlarge. The water-blocking ratio of 7% is a significant demarcation value for the backwater height in front of bridges on plain rivers. Thus, the water-blocking ratio of medium and large bridges should not be more than 7%.

plain river;backwater of piers; water-blocking ratio; numerical simulation; creep height in front of piers; backwater height in front of a bridge

10.3876/j.issn.1000-1980.2016.05.002

2016-01-28

水利部重大公益性行业科研专项 (201501007);国家自然科学基金(51479058);国家自然科学基金重点基金(51239003)

王玲玲(1966—),女,江苏射阳人,教授,博士,主要从事水力学数值模拟研究。E-mail:706584934@qq.com

通信简介： 唐洪武,教授。E-mail:hwtang@hhu.edu.cn

U442.3

A

1000-1980(2016)05-0386-07