Matlab绘图功能在高等数学教学中的应用

张建勇，肖慧娟，赵一方，马会礼

（1.河海大学　数理教学部，江苏　常州　213022；2.河海大学　物联网学院，江苏　常州　213022；3.河海大学　企业管理学院，江苏　常州　213022）

Matlab绘图功能在高等数学教学中的应用

张建勇1，肖慧娟2，赵一方3，马会礼1

（1.河海大学数理教学部，江苏常州213022；2.河海大学物联网学院，江苏常州213022；3.河海大学企业管理学院，江苏常州213022）

针对高等数学教学过程中，学生在绘图方面存在的困难，提出将Matlab作为辅助教学软件，来提高教与学的效果，给出了若干函数的绘图和程序，提供了两个教学案例。

Matlab；高等数学；平面图形；空间图形

0　引言

在高等理工科院校中，高等数学［1］（以下简称高数）是一门非常重要的基础课,是学生学习后继基础课和专业课程的基础。高数的抽象性使得在教与学的过程中缺乏生动性和直观性。学生在学习高数的过程中普遍存在一个现象就是不能够正确绘制函数图像，导致一些内容难以理解，比如：振荡间断点、Taylor展开式、空间曲面、重积分等。出现这种问题的原因在于：（1）中学阶段以培养计算能力为主，所用函数主要是一元显函数，大学阶段研究的函数种类多而且复杂，如隐函数、参数方程所确定的函数、极坐标函数、多元函数等；（2）描点法已经不能满足高数中函数的绘图需求，如空间函数图形等很难绘制。

随着计算机应用的快速发展，在教学过程中引入软件辅助教学，是教学改革的一个部分。Matlab［2］软件具有出色的计算功能和图像处理能力，已经得到教学和科研人员的高度认可。其强大的绘图功能不仅体现在绘制曲线和曲面上，还体现在绘制不同坐标系下的图形。正是这种能力为函数的图形化（即可视化）提供了有力工具，使得函数得到更加形象生动的展示，有利于揭示函数的内在特性。

本文结合高数的教学，讨论Matlab软件在平面图形、空间图形、微分学等方面的一些应用。

1　平面图形

高数的研究对象是函数，高数中有些函数是高中没有涉及的，如隐函数、极坐标函数等。这些函数过于抽象，在Matlab中plot、ezplot和polar等命令可以使得这些函数更具直观性。

1.1plot命令

plot是Matlab绘制二维图形的最基本命令，主要用来绘制显函数，调用格式为：plot（x，y，options）,其中x表示横坐标向量，y表示纵坐标向量（函数值），options可以对图像的颜色、线条宽度等进行修饰。比如绘制y=arctan x，如图1所示。

1.2ezp lot命令

高数中经常用到隐函数、参数方程等，这些函数的图像用plot命令绘图是很复杂的，而ezplot却很简单。其调用格式为：ezplot（f，options），其中f为函数的符号表达式，options可以对坐标进行设置等，默认坐标范围是-2π≤x，y≤2π。图2为绘制的心形线、摆线、三叶玫瑰线和伯努利纽线。程序如下：

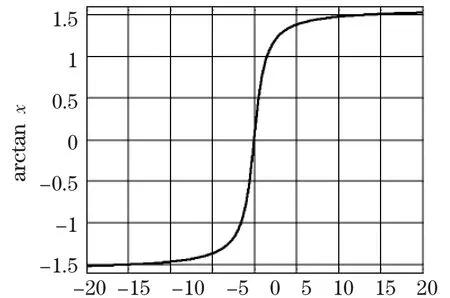
图1　plot绘制arctan x的图像　

图2　ezplot绘图

1.3极坐标图形的绘制

在高数中，涉及极坐标的知识点为弧微分、积分求面积和曲线积分等，在不了解极坐标表示的图像的情况下，有时难以运算。Matlab中提供了polar命令，调用格式为polar（theta，rho），其中theta是弧度表示的角度，rho表示极径，图3是传说的笛卡尔［3］最后一封情书中蕴含的秘密ρ=a（1-sinθ）的图形。程序为：

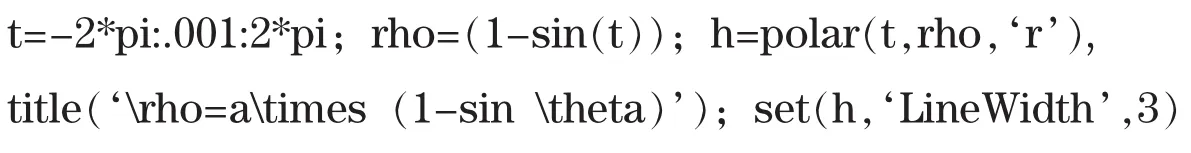
2　空间图形

空间曲线和曲面在高数中占有重要的地位，在三重积分和曲线曲面积分的计算中起着关键性的作用。其表达式均是由三元方程表示，对于空间想象力不好的学生来说，绘制三维图像有很大的难度。下面结合高数中常见的空间图形，分别举例讨论空间曲线和曲面的绘图。

2.1空间曲线

绘制空间曲线所用的命令是plot3,调用格式为：plot3 （x，y，z，options），其中参数x、y、z都是变量，options是曲线的样式参数。图4是螺旋线，matlab程序如下。

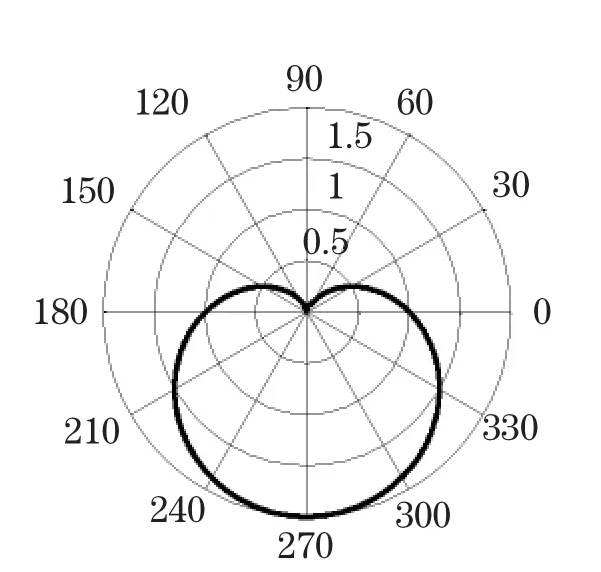
图3　polar绘制心形线

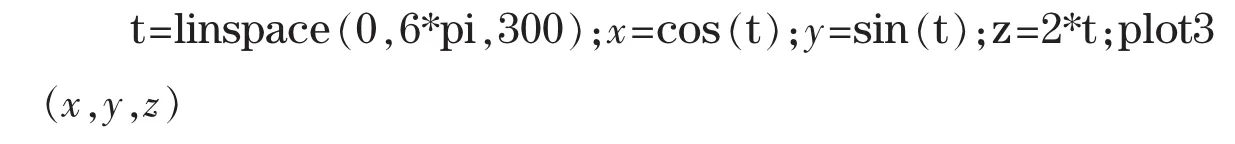
2.2空间曲面

高数中常见的空间曲面主要有球面、柱面、锥面、旋转曲面等，Matlab中提供了丰富的绘图命令，如plot、mesh、surf、ezmesh、ezsurf等，相比较而言，ezmesh和ezsurf在使用过程中相对简单，另外，在绘制空间曲面时，动态演示的课堂效果会更好。图5是锥面z2=9（x2+y2）的动态演示程序和三个截图。

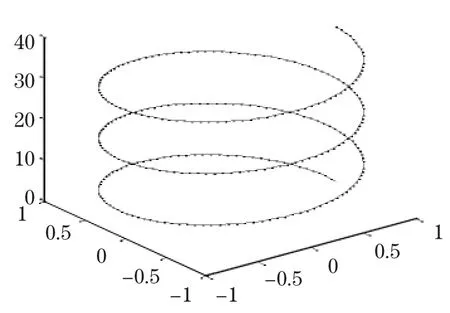
图4　plot3绘制螺旋线

图5　动态演示锥面的截图

3　在微积分中的应用

3.1间断点

如何分析及其判断间断点类型，对学生来说也是一个难点。主要原因是对知识的理解不够清晰。借助图像，有助于学生直观地理解该内容。图6是在x=0附近的图像。

图6　无穷振荡间断点

3.2微分方程的数值求解

在高数中讲解微分方程的主要目的是为后续的专业课打基础，如在电路、线性系统中，很多系统都是用微分方程描述，如何判断系统的稳定性是重要学习内容，其中一种方法是利用解析解判断系统是否稳定。但能够求得解析解的微分方程很少，尤其是非线性微分方程，这时数值解或者仿真就是一个很好的途径［4］。例如x"+0.5x'+2x+x2=0，这是一个非线性微分方程，无法获得它的解析解，编写Matlab程序，调用ode45命令绘制未知函数x（t）图像，如图7所示。

图7　微分方程的数值模拟

主程序为

尽管我们无法通过解析解分析该微分方程的稳定性，但是通过仿真得到的图像可以看出，随着时间的不断增加，该系统趋于稳定状态。

4　其他应用

除上述情况外，还可以在Taylor级数、幂级数、Fourier级数中，应用matlab的绘图功能来展示函数及其展开式之间的联系。图8中虚线是指数函数ex，实线是ex幂级数展开式的图像。

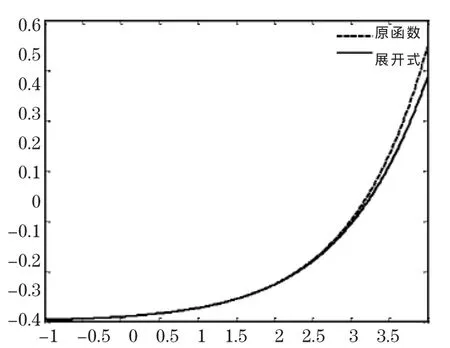
图8　幂级数展开式对比图像

5　教学案例

在高数教学过程中，Matlab作为辅助工具，不宜占用过多的课堂时间，下面举两个我在教学过程中使用过的案例。

案例1在讲授基本初等函数的时候，由于高中教学改革的原因，三角函数与反三角函数有些是不讲授的，如y= sec x、y=csc x、y=arctan x等，而在高数中微积分学中是一个重要内容。如何快速掌握这些函数是很关键的，结合函数图像给学生展示和讲解，学生就很容易理解它们的各种性态。图9是通过Matlab绘制的四个三角函数的图像，这里就不再赘述反三角函数图像。程序如下：

案例2在微分方程一章的授课中，通过Matlab数值求解的结果与解析解进行比较，并给学生说明在实际工程应用中，数值解往往比解析解更为重要。例如微分方程y"+4y'+y=0满足初始条件y（0）=1，y'（0）= 0的解析解为y=（1+0.5x）e-0.5x。从图10中可以看出，数值解和解析解几乎吻合。程序如下

主程序如下：

图9　案例1图像　

图10　案例2图像

在高数教学过程中，有很多地方可以使用Matlab软件，绘图只是其中之一。在辅助教学的绘图方面，这两个案例比较具有代表性，需要教师在课前调通程序，在讲课的过程中，每个程序的现场演示及说明所用时间为3m in左右。在不占用过多的课堂时间的条件下，丰富了课堂内容，这比单纯使用PPT演示更具说服力。

6　总结

引入Matlab辅助高数的教学，对教师来说，可以丰富自己的教学手段、内容和形式。对学生来说，有助于提高学习兴趣、促进学以致用，课堂会更加生动、形象。

Matlab界面友好，编程简单，使其在很多领域得以应用。目前关于Matlab的教程非常丰富，除在高数中的应用外，在概率统计、线性代数的教学中也可以得到很好的应用。

［1］同济大学数学系.高等数学［M］.（7版）.北京:高等教育出版社，2014.

［2］周建兴.MATLAB从入门到精通［M］.（2版）.北京：人民邮电出版社，2012.

［3］http://baike.baidu.com/link?url=OGMDxZf7iKqf-TBjrFtUq_TjQ9nfjDAjkvn InCiqHX87w k5KiKU-yTBeLYXy7H3pw TvOjU8bm UFu7N40fMeC5q

［4］张建勇，陈亮，陈雨儿，等.基于MATLAB的微分方程课堂教学设计［J］.教育教学论坛，2014（52）:168-169.

App lication of M atlab Draw ing Function in the Teaching of Advanced Mathematics

ZHANG Jianyong1，XIAO Huijuan2，ZHAO Yifang3，MA Huili1
（1.Department of Mathematics and Physics,Hohai University,Changzhou 213022,China; 2.College of Internet of Things Engineering,Hohai University,Changzhou 213022,China; 3.College of Business Adm inistration,Hohai University,Changzhou 213022,China）

In the process of Advanced Mathematics teaching,students sometimes may have difficulty in draw ing.To solve the problem,this paper presents Matlab as an auxiliary teaching softw are w hich can improve the teaching and learning effects.As a result,it provides several figures of functions and procedures,and also offers two teaching cases.

Matlab,Advanced Mathematics,plane graph,spatial graph

10.13853/j.cnki.issn.1672-3708.2016.03.014

（责任编辑：耿继祥）

2015-07-01；

2016-03-01

张建勇（1978-），男，山东平邑人，副教授，博士，研究方向：随机微分方程的稳定性与数值解法。