人员疏散预动作时间的随机性研究
毛占利,陈浩楠
(武警学院 消防工程系,河北 廊坊 065000)
人员疏散预动作时间的随机性研究
毛占利,陈浩楠
(武警学院 消防工程系,河北 廊坊065000)
人员疏散中预动作时间会在很大程度上影响到人员能否成功安全疏散,鉴于火情发展和人员心理、生理、消防安全意识等问题,预动作时间往往存在着较大的随机性。采用核密度估计的方法,以实际火灾案例中人群疏散预动作时间为样本进行分析,用统计学规律表征预动作时间的随机性。研究表明:人员疏散预动作时间满足一定的概率分布规律。
预动作时间;随机性;概率密度函数;累积分布函数;核密度估计
0 引言
近年来,随着我国经济水平的快速发展,各种各样的建筑不断涌现,如高层建筑、超高层建筑、大型地下建筑等,这些建筑往往具有人员密度大、可燃物较多等特点。一旦发生火灾,建筑的安全疏散功能将会面临巨大考验,在疏散条件不利的情况下,容易造成群死群伤火灾事故。因而,对紧急情况下建筑内人员疏散问题的研究越来越受到人们的重视,而在人员疏散中预动作时间会在很大程度上影响到人员能否成功安全疏散[1-2]。鉴于火情发展和人员心理、生理、消防安全意识等问题,预动作时间往往存在着较大的随机性,因此,对人员疏散预动作时间的研究显得尤为必要。对于人员预动作时间的随机性问题,国内外学者开展了一定的研究工作,并取得了一定的研究成果。Maclennan[3]得出人员疏散时间可用Weibull分布进行表示;Purser[4]等人通过大量的试验,认为偏态分布可以较好地描述预动作时间分布规律;褚冠全[5]在使用GridFlow疏散模型研究预动作时间及出口宽度对人员疏散的影响时,以预动作时间服从正态分布(Normal Distribution)为试验前提;陈涛[6]在其所建立的CFE模型中也采用了正态分布表征预动作时间,同时指出正态分布的均值和方差可以根据人员疏散的具体情境进行设定。本文主要以人员疏散过程中的预动作时间为研究对象,以真实的火灾调查数据为基础,尝试使用概率密度函数进行估计的方法,在前人的基础上对预动作时间的随机性问题进行研究。
1 预动作时间随机性研究的理论基础
1.1随机性问题分析
预动作时间是指建筑内人员从发现险情到开始疏散动作时所经历的时间。在火灾情境中,不同的人发现火情后的预动作时间是不同的。据John L.Bryan[7]的研究结果,人们在发现火灾后,当处于疏散行为发生前的这段时间时,可能会随机进行各种各样的非逃生动作,且这些动作在不同文化背景的人群中发生的比例也不尽相同。
行为反应可能会受到起火点远近、火情大小、当事人心理和生理状态、建筑物结构和平面布置、建筑内火灾自动报警系统动作情况等多方面因素的影响。因此,人员预动作时间显然会出现随机性,如果用传统的安全系数法等方法处理预动作时间数据,那么所得结果与实际将会有所偏差。
1.2随机性问题处理方法
1.2.1概率密度函数估计
概率密度函数是用于描述某个连续性随机变量(如时间)的输出值在某个确定取值点附近的可能性的函数。满足以下性质:

(1)
(2)
(3)
从遵循某个分布规律的一组已知数据中估计出该连续型随机变量的概率密度函数的过程,叫作概率密度函数估计的过程。预动作时间的统计数据是研究预动作过程随机性的第一手资料,通过分析人员在火灾场景中的行为特征,结合统计出的疏散时间数据,尝试用概率密度函数对时间分布规律进行表述。
对于某个随机变量,获取其概率密度函数的方法主要有含参估计法、无参估计法和半参估计法[8]。与概率密度函数相同,累积分布函数同样也可以用于表示时间变量的随机性特征。其定义为随机变量小于或者等于某个数值的概率P,即F(x)=P(X≤x)。将概率密度函数进行积分,便可得到对应的累积分布函数。
1.2.2估计方法的选取
由上所述可知,多种类型的概率密度函数估计方法的存在,决定了必须要视实际情况选取合适的途径进行数据处理。对于一组数据,如何选取概率密度函数的估计方法很大程度上决定了能否得出理想的结果。在诸如海杂波等自然现象研究领域,常用含参估计的方法[9],因为自然界诸多现象可以用正态分布等特征已知的分布函数进行规律描述,且模型中考虑的影响参数较少,操作起来相对简单。但是在处理海杂波非平稳性问题时,含参估计的方法仍存在一定局限性[10]。与含有未知参数的计量模型相比,非参数化模型对求概率密度函数不具有选择性。核密度估计对数据的经验分布不做任何假设,主要是从样本中获取分布信息,其定义如下:
假设{X1,X2,…,XN}为一元随机变量x的N个样本,在任意点x处的总体密度函数的核密度估计记为:
(4)
式中,K()称作核函数(kernel function),要求K()满足以下条件:

(5)
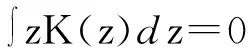
(6)
(7)
常用的核函数有高斯核(Gaussian Kernel)、均匀核(Uniform Kernel)、三角核(Triangular Kernel)、伊潘涅切科夫核(Epanechnikov Kernel)等(见表1),它们具有对称性和单峰的特点,可以用来对分布规律较为简单的数据进行核密度估计。

表1 核密度估计中常用的核函数
鉴于人员疏散预动作时间相关问题研究中,需要考虑的因素的多样性和复杂性,本文直接采用核密度估计法展开分析。
2 预动作时间的随机性问题研究
2.1原始数据的获取
1993年2月26日,位于美国纽约的世贸大厦地下车库发生爆炸,进而引发火灾。建筑遭受严重损坏,火势迅速危及建筑的主体部分,即世贸中心双子塔。其中,距离爆炸发生地较近的塔一(记为WT1)比塔二(记为WT2)受损程度严重。两栋建筑内所有人员的疏散过程总共持续了5 h,事故造成6人死亡,1 000多人受伤。事后,美国消防协会和加拿大国家研究委员会对从火灾中成功疏散出来的人员进行了问卷调查,并将相关统计结果予以公布。
根据Rita F.Fahy和Guylene Proulx[12]所提供的数据资料,对相应的统计数据[1]进行处理后,可以得到表2所示的结果。根据预动作时间的定义,可以将该案例中的时间具体分为发现异常、得知火情、开始疏散三个阶段。两幢建筑中的人群几乎在同一时刻察觉到有异常情况发生,但是由于WT2距事故发生地较远,信息传递受到一定阻碍,得知“有爆炸发生”的时间相对滞后。此外,WT2中人员是在被消防员告知才意识到需要进行疏散,因此WT2的疏散过程耗时较长。两幢建筑疏散的平均预动作时间显然有较大差距,这也与表中数据相吻合。
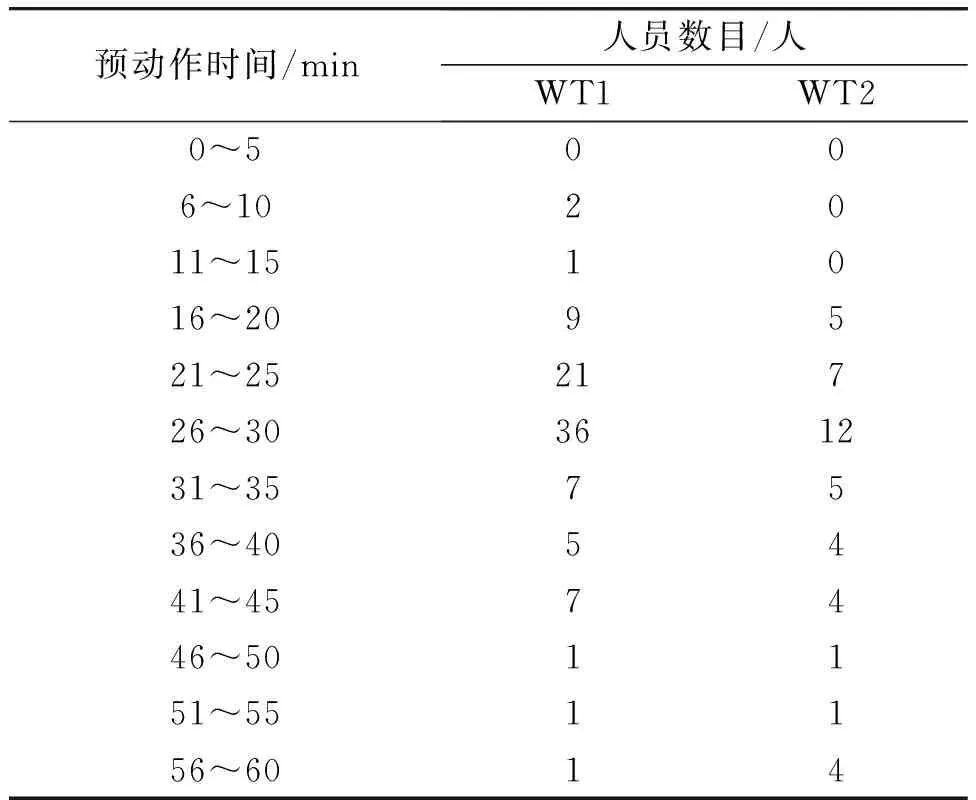
表2 两幢建筑内人员的预动作时间
2.2WT1预动作时间随机性分析
2.2.1预动作时间的核密度估计
在MATLAB环境下对WT1中人员疏散预动作时间进行处理分析,当采用默认的最佳窗宽和Gaussian核函数时,对其进行核密度估计,并与服从原始数据特征的N(28,9.99982)分布密度图进行对比,如图1所示。可以看出,在默认窗宽h=3.822 5的条件下,利用Gaussian核函数求出的核密度曲线与N(28,9.99982)分布的密度曲线非常接近,与预动作时间的频率直方图每段区间较为吻合,说明核估计具有较低的失效概率。可以认为,WT1内人员疏散的预动作时间近似服从高斯分布,在火灾发生30 min才开始疏散的人员居多,早于或晚于这个时间进行疏散的人员呈逐渐减少的趋势。在对类似建筑安全疏散设计时,可以结合此规律考虑人员疏散的随机性现象,做到既不过度设计,又能保证安全。
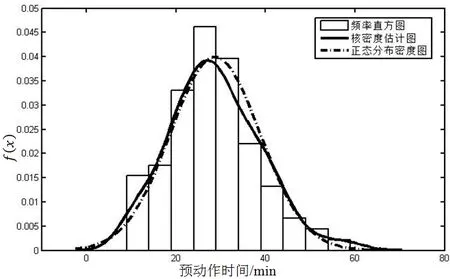
图1 核密度估计结果与正态分布对比图(WT1)
2.2.2窗宽对核密度估计的影响
为了探究窗宽的设置对核密度估计结果准确度的影响,将固定核函数为Gaussian核函数,在不同窗宽条件下进行试验,观察核密度估计的结果随试验条件的变化产生的不同。从图2和图3可以看出,不同窗宽下,核密度估计值及其曲线形状差距较大。以最优窗宽hm=3.822 5为界,对于较小的窗宽值,核密度估计曲线比较曲折,光滑性很差,反映了较多细节,但是已经失去了规律性;对于比较大的窗宽值,核密度估计曲线比较平滑,但是掩盖了较多的细节,存在着数据失真的现象。因此本文选用窗宽h=3.822 5是比较合适的。
2.2.3核函数对核密度估计的影响
由表1可知,在核密度估计中有多种核函数可供选择,但是根据核密度估计的原理,对估计结果产生影响的主要是窗宽的选取,核函数的不同对拟合结果产生的影响较为微弱。选取默认的最佳窗宽作为固定值,改变核函数,观察不同核函数对核密度估计结果的影响,结果如图4和图5所示。由图可知,不同的核函数的选取对核密度估计的结果不会造成决定性影响,结果的差异仅仅体现在曲线的光滑程度上。
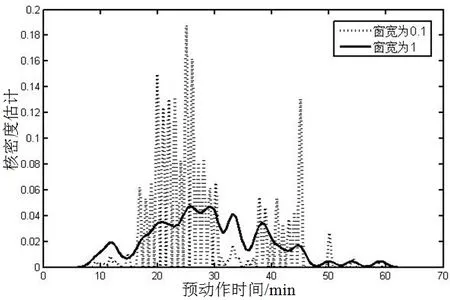
图2 小窗宽条件下的核密度估计
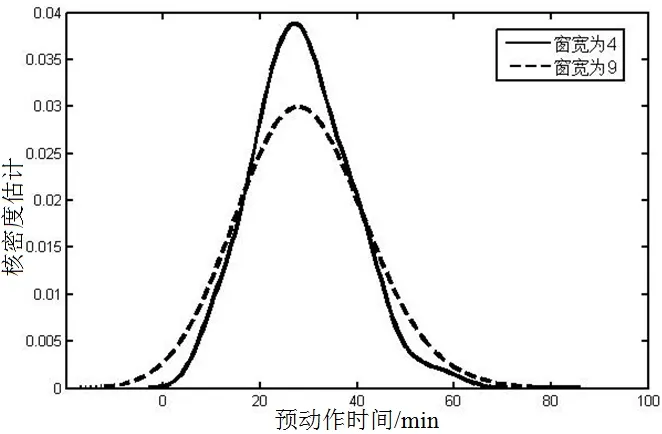
图3 大窗宽条件下的核密度估计

图4 第一组核函数对比图

图5 第二组核函数对比图
2.2.4预动作时间累积分布的核估计
采用默认的最佳窗宽和默认的Gaussian核函数,对累积分布函数进行核估计,将估计的结果与样本经验分布函数和N(28,9.99982)分布的分布函数图像进行对比,如图6所示。经验分布函数是累积分布估计的重要结果之一,其图像特性呈阶梯状,直观反映了预动作时间的分布情况。图中经验分布函数与均值为28、标准差为9.9998的正态分布的累积分布函数图像附和效果明显,且成典型的S型走势,也就说明WT1的预动作时间近似服从正态分布N(28,9.99982)。

图6 累积分布函数的核估计结果(WT1)
2.3WT2预动作时间随机性分析
与WT1的预动作时间分析思路相同,采用核密度估计的方法对表2第二组数据进行处理,结果如图7所示。通过绘制的频率直方图可以得知,存在两个时间点,此刻开始进行疏散的人员数量将会达到峰值。核密度估计图呈双峰非对称分布,由N(22,132)和N(63,182)两个正态分布组合而成的混合型双峰分布与核密度估计的结果附和性良好。该分布特点说明人员疏散预动作时间出现了两极分化的现象,可能是由于WT2离爆炸发生地比较远,

图7 核密度估计结果与混合分布对比图(WT2)
WT2内一部分人员对火情信息的接收受到了延滞,当同一栋建筑内其他部位人员疏散进行了一段时间后,信息才传达到受阻碍区域,进而出现了第二次疏散峰值,但疏散强度已明显不如第一次峰值。
图8也充分体现了概率密度双峰分布的特点,预动作时间曲线呈现“双S”发展趋势,有两个明显的拐点,表明概率密度函数两次达到极大值。与概率密度函数相比,对累积分布函数的核估计更为简便,不需额外信息的添加。在利用疏散时间分布规律进行人员疏散模拟试验时,还可直接根据累积分布曲线产生人员疏散的预动作时间。

图8 累积分布函数的核估计结果(WT2)
3 结论
本文重点讨论了人员疏散过程中预动作时间的随机性问题,在总结前人经验的基础上,尝试用核密度估计的方法得出预动作时间的概率密度函数和累积分布函数,表述了随机性这一抽象概念,同时得到了如下结论:(1)预动作时间可以使用概率密度函数进行表征,其值满足一定的概率分布规律;(2)预动作时间的概率分布规律受到环境、人员自身等因素的影响,建议采用核密度估计的方法,可以使函数拟合的过程大大简化。
[1] 汪金辉.建筑火灾环境下人员安全疏散不确定性研究[D].合肥:中国科学技术大学,2008.
[2] 吕勇.公路隧道火灾人员逃生不确定性研究[D].西安:长安大学,2013.
[3] MACLENNAN H A,REGAN M A,WARE R.An Engineering Model for the Estimation of Occupant Premovement and Response Times and the Probability of Their Occurrence[J].Fire and Materials,1999,23(6):255-263.
[4] PURSER D A,BENSILUM M.Quantification of Behavior for Engineering Design Standards and Escape Time Calculations[J].Safety Science,2001,38(2):157-182.
[5] 褚冠全,孙金华,王青松,等.疏散准备时间及出口宽度对人员疏散影响的模拟[J].科学通报,2006,51(6):738-744.
[6] 陈涛.火灾情况下人员疏散模型及应用研究[D].合肥:中国科学技术大学,2004.
[7] BRYAN J L.Behavior Response Offire and Smoke[M].3rd ed.SFPE Handbook of Fire Protection Engineering,2002.
[8] 张玉敏.基于不同核函数的概率密度函数估计比较研究[D].保定:河北大学,2010.
[9] 杨杰,卢凌,陆济湘.海杂波概率密度分布函数分析方法的研究[J].武汉交通科技大学学报,1998,22(1):51-54.
[10] 杨永生,张宗杰.基于核函数和带宽的海杂波概率密度函数估计[J].探测与控制学报,2010,32(5):38-41.
[11] 谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010.
[12] FAHY R F,PROULX G.Human Behavior in the World Trade Center Evacuation[C]//Proceeding 5th International Symposium on Fire Safety Science.Melbourne,Australia,1997:713-724.
(责任编辑、校对李蕾)
Random Research on the Pre-evacuation Time of Occupant Evacuation
MAO Zhanli, CHEN Haonan
(DepartmentofFireEngineering,TheArmedPoliceAcademy,Langfang,HebeiProvince065000,China)
Pre-evacuation time will greatly affect occupant evacuation, and it has a large randomness due to fire development, human psychology, human physiology, fire safety awareness and so on. Kernel density estimation is adopted in this paper based on the samples from a real fire case, the randomness is characterized using statistical rules. The results show that pre-evacuation time of occupant evacuation can fit certain probability distribution rule.
pre-evacuation time; randomness; probability density function; cumulative distribution function; kernel density estimation
2016-02-02
国家自然科学基金(51508571);河北省自然科学基金(E2016507012);河北省教育厅基金(Z2015071)
毛占利(1982—),男,河南台前人,讲师,博士,主要从事人员安全疏散方面的研究; 陈浩楠(1994—),男,河南许昌人。
D631.6
A
1008-2077(2016)04-0048-05

