一种抗SDIF分选的脉冲重复间隔参差设计方法
张保群
(中国西南电子技术研究所,成都 610036)
【信息科学与控制工程】
一种抗SDIF分选的脉冲重复间隔参差设计方法
张保群
(中国西南电子技术研究所,成都610036)
为提高雷达对电子侦察系统抗分选识别能力,从破坏脉冲重复间隔(PRI)分选性能的角度出发,提出了一种雷达信号PRI参差设计方法。根据典型的序列差值直方图(SDIF)算法的工作流程,分析了SDIF实现PRI参差信号分选的关键步骤。合理设计参差PRI取值,使其满足一定约束条件,可以破坏正确分选流程,达到分选结果中目标增批的目的。仿真结果表明,该设计方法能有效对抗基于SDIF的信号分选策略,可以为雷达信号射频隐身设计提供初步的理论指导。
抗分选; PRI参差; 序列差值直方图;雷达;射频隐身
电子侦察通过对有源传感器辐射的电磁信号进行截获、测量、分选和识别,可以获取辐射源的技术参数、类型、用途和位置等情报信息。电子侦察是实施电子攻击和电子防护的前提和基础[1]。现代电子侦察技术的快速发展,对雷达构成了越来越大的生存威胁[2]。为提高战场生存能力,现代雷达也逐渐开始采用一种射频隐身技术即对电磁信号特征进行缩减和控制的技术,典型的技术措施包括辐射功率控制、低副瓣天线设计、低截获概率波形设计等[3-4]。上述措施的主要着眼点在于降低侦察接收机对雷达信号的截获概率。实际上,雷达执行任务时通常会遇到各种类型的电子侦察设备,不可能寄希望于雷达信号永远不被截获,因此削弱侦察设备的分选识别能力应成为射频隐身技术的另一个关键突破点[5]。
为对抗电子侦察的信号分选功能,目前国内学者已经开展了初步研究[6-10]。文献[6-7]从抗多参数聚类分选的角度,提出构造合适的干扰信号,降低辐射源脉冲聚类的准确度,以达到避免雷达信号参数被正确提取的目的。与采用角度、频率、脉宽等多参数的联合预分选相比,脉冲重复间隔(PRI)分选一直以来是信号分选中研究最多、成果最为丰富的方法[11-14],并且PRI特征是雷达信号最为重要的一维特征,其值往往直接与雷达的属性、用途和工作方式有关,PRI特征的正确识别能为情报生成提供可靠的依据[1,15]。因此,文献[9-10]侧重从抗PRI分选的角度进行了研究,提出在雷达信号中有规律地加入干扰脉冲使得累积差值直方图(CDIF)或PRI变换法等分选算法无法提取真实脉冲序列,从而达到保护雷达PRI参数的目的。
然而,无论是抗多参数聚类分选、还是抗PRI分选,上述文献的主要思路几乎都是在信号中按一定规则加入干扰脉冲,达到使得信号分选获取错误或虚假的雷达参数特征、或者增加分选处理时间的目的。这些策略从理论上来讲,抗分选效果是比较明显的。不过,在实际应用中,上述策略具有一定的随意性,对于雷达信号设计来说,还不能给出规范化的、定量的指导;并且,还需要考虑如何保证发射的干扰脉冲不对雷达自身构成干扰。这给雷达信号的设计带来了较大的难度。为克服上述问题,本文从雷达信号自身的PRI特征设计出发,针对工程中常用的序列差值直方图(SDIF)分选算法,在尽可能不影响雷达任务性能的前提下,给出了一种PRI参差定量设计方法,以达到抗分选目的。
1 基于SDIF的PRI参差信号分选
SDIF和CDIF都属于TOA差值直方图分选方法,其思想是依次对各级TOA差值直方图统计分析和门限检测,确定可能存在的辐射源PRI,然后根据这些可能的PRI进行序列搜索,将辐射源脉冲序列提取出来[11,12]。SDIF和CDIF具有算法简单、对随机干扰脉冲和脉冲丢失不敏感的特点,可适用于PRI固定、PRI参差和PRI抖动的雷达信号分选,因此在工程中得到了广泛应用[15-17]。
SDIF对CDIF进行了两方面改进:一、不对不同级的直方图统计值进行积累,仅检测当前级的直方图,同时取消了2倍PRI检测,减少了计算量、提高了处理速度;二、具有最佳的检测门限,配合子谐波检测,可以避免PRI谐波可能引起的虚假检测。本文下面的抗PRI分选设计,主要针对SDIF算法展开。
PRI参差雷达是采用两个或两个以上的PRI,通过顺序、重复地利用PRI集合中的PRI值产生脉冲序列。PRI参差主要用在动目标显示雷达中消除盲速,或在一些搜索雷达中消除模糊[18]。由于PRI参差脉冲序列可看成多个具有相同PRI的常规脉冲序列的交错,可以按照适用于PRI固定的分选方法对其进行分选,分选出多个PRI固定的脉冲序列后,如果能识别为同一辐射源的脉冲序列,再合并即可得到PRI参差脉冲序列[1,15]。因此,SDIF和CDIF等直方图算法,尽管主要是针对PRI固定信号分选提出的,但通过对分选结果进一步做参差分析,可分选出PRI参差雷达信号[11,16,17]。
下面结合SDIF算法流程,给出SDIF分选PRI参差信号的原理和步骤。
1.1SDIF分选流程
SDIF的算法流程如图1所示[12]。
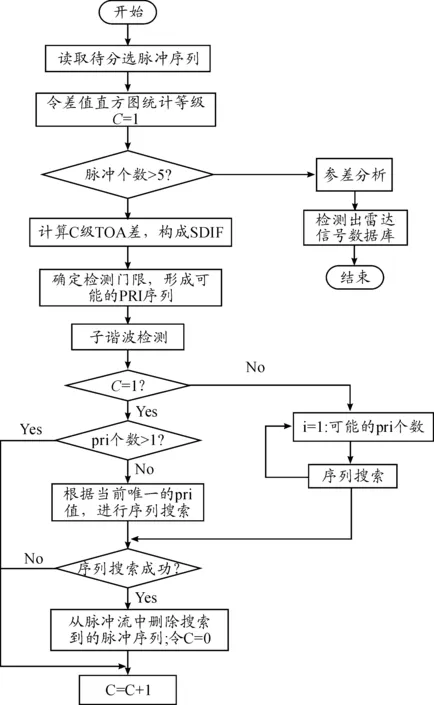
图1 SDIF算法流程
图1中SDIF算法主要包括TOA差值直方图分析和序列搜索两部分[12]。
TOA差值直方图分析用于PRI估计,通过对各级TOA差值出现次数进行直方图统计,若某一级直方图中存在过检测门限的峰值,则将停止更高级别的TOA差值统计,而将峰值对应的TOA差值作为可能的PRI估计值。这里,一级TOA差是指任意相邻脉冲到达时间之差即ti+1-ti(脉冲序号i=1,2,…,N-1,N为脉冲总个数),对其出现次数的直方图统计称为一级直方图;二级TOA差是间隔一个脉冲的任意两个脉冲到达时间之差即ti+2-ti,对其出现次数的直方图统计为二级直方图;其他级别直方图依次类推。
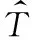
1.2参差分析
在实际工程中,PRI分选往往是和多参数联合预分选或聚类是级联使用的,即交错脉冲流先经过预分选,然后再进行PRI主分选。预分选的结果是角度、频率、脉宽等参数相近的脉冲序列[14,15]。因此,对于PRI参差的雷达信号,采用SDIF进行PRI主分选后,会分选出多部角度、频率和脉宽相似、PRI值接近且PRI固定的雷达,并且PRI值等于骨架周期即参差信号各子PRI之和[15,16]。根据这一特点,可以对分选结果中PRI接近的辐射源脉冲序列合并,按TOA由小到大排序,进行一级直方图统计。如果能得到多个峰值接近的PRI,并且PRI之和等于骨架周期,则判断该信号为参差信号,各PRI为参差信号的子PRI[1,16]。具体参差分析流程如图2所示。
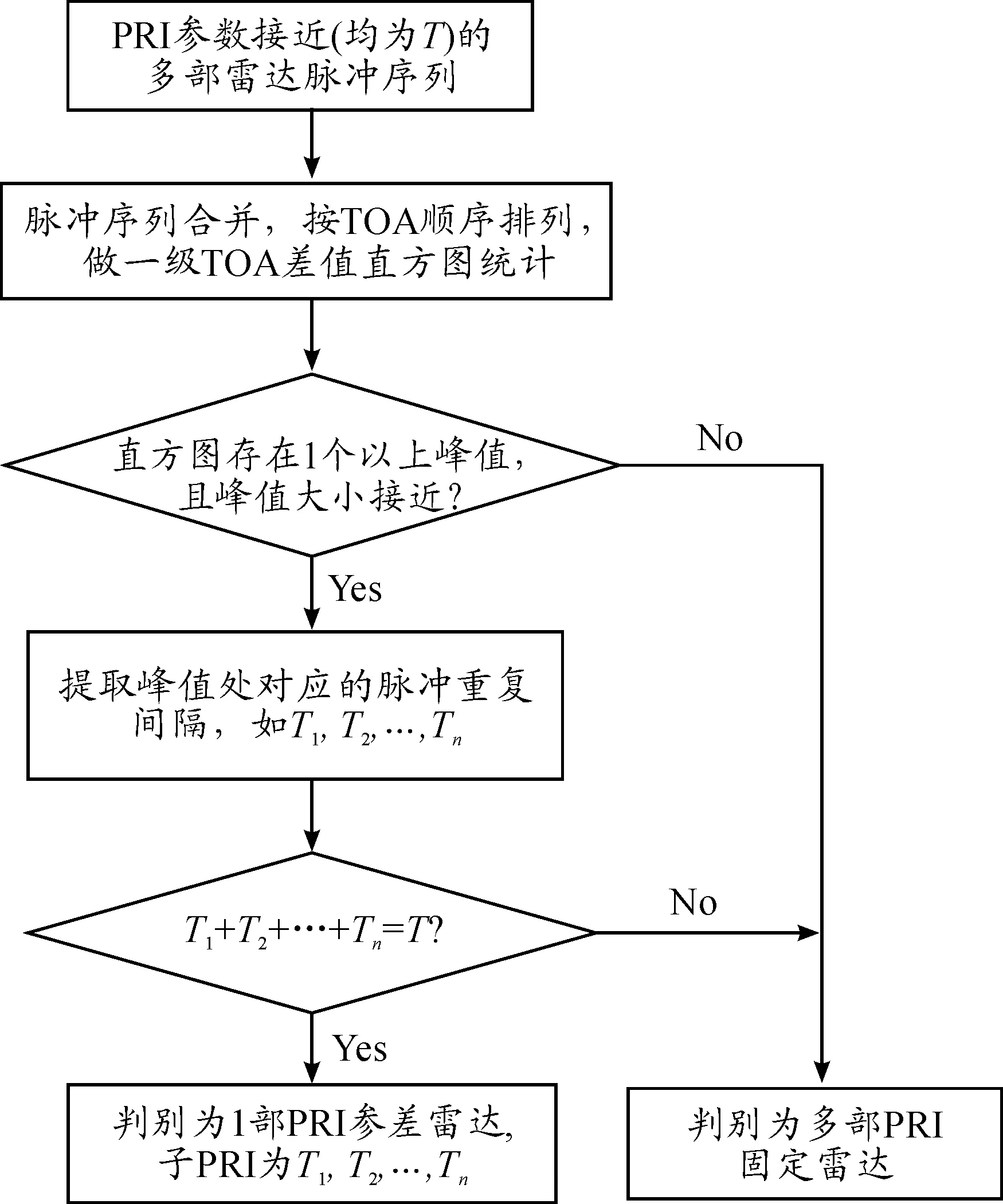
图2 PRI参差分析流程
2 抗SDIF分选的PRI参差设计
从上一节分析可以看到,SDIF分选PRI参差雷达信号的关键步骤为:
步骤1:按PRI固定的分选流程,分选出PRI相近(其值等于骨架周期)的n个PRI固定雷达;
步骤2:对步骤1中的n个PRI接近的雷达脉冲序列进行参差分析。
因此,如果能适当设计参差信号的子PRI取值,使得步骤1中SDIF分选出多部PRI值不相同的雷达,那么就不会进入图2的参差分析流程,最后导致目标增批。鉴于图 1中SDIF分选又包括TOA差值直方图分析和序列搜索两个步骤,要破坏上述步骤1,子PRI取值需使得二级及二级以上直方图存在对应非骨架周期的虚假峰值,并且采用虚假峰值对应的PRI能成功进行序列搜索。
通常PRI参差雷达的子PRI个数为2~7[14],因此下面主要针对2~7参差脉冲信号,从其各级TOA差值直方图统计特性入手,给出抗SDIF分选的PRI具体设计要求。
记PRI参差雷达第i+1个脉冲的到达时间为:
(1)
其中:i=1,2,…,N-1;Tj∈{T1,T2,…,TM}表示第j个子PRI值,M为PRI参差个数;{T1,T2,…,TM}为参差PRI集合;mod(i,M)表示i对M取余数。为给出定量设计规律,本文要求参差PRI之间呈等间隔递增关系(类似PRI滑变的情况[14-15]),即
(2)
其中,Δ>0为恒定的参差增量。
2.1参差信号
对于2参差信号,理想情况下其TOA差值直方图统计结果如图3所示。
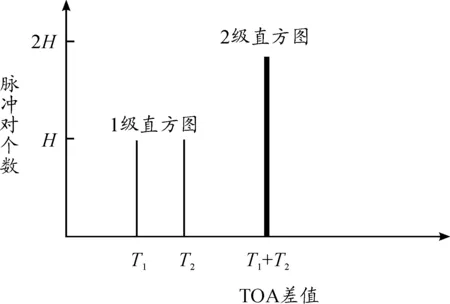
图3 2参差信号TOA差值直方图
由图3可以看到,2参差信号的一级直方图在T1和T2处有两个等高度的峰值,二级直方图在骨架周期(即T1+T2)处有唯一峰值。根据图 1中SDIF算法流程,若一级直方图过检测门限的PRI个数大于1,不进行序列搜索,进行二级直方图统计。根据二级直方图峰值对应的骨架周期进行序列搜索,可挑选出PRI固定且其值等于骨架周期的1部雷达脉冲序列,如图4所示。剩余脉冲重新进行一级直方图统计,会在骨架周期处形成唯一的峰值,进而序列搜索后又分选出1部PRI等于骨架周期的雷达。最后,按照图 2进行参差分析,2部PRI相同的雷达会合并为1部PRI参差的雷达。

图4 2参差信号序列搜索示意图
综上分析,SDIF恒适用于2参差信号分选,即无论如何设计子PRI即T1和T2的值,都不会影响SDIF对2参差信号的分选性能。
2.2参差信号
对于3参差信号,理想情况下其TOA差值直方图统计结果如图5所示。
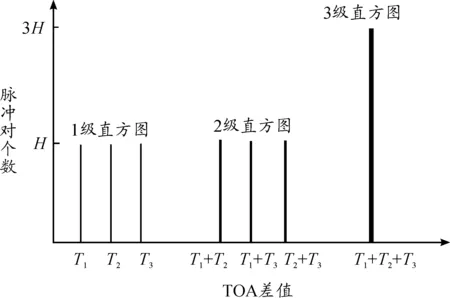
图5 3参差信号TOA差值直方图
由图5可以看到,3参差信号的一级直方图有3个峰值,二级直方图有3个峰值,三级直方图在骨架周期处有唯一峰值。根据SDIF算法流程,若二级直方图有峰值过门限,按照对应的PRI进行序列搜索,则有可能会提取出PRI不等于骨架周期的雷达脉冲序列。具体来说,假设二级直方图的3个峰值均过门限,若子PRI满足:
(3)
根据图1中序列搜索原则,当以3个峰值值中对应的最小PRI即T1+T2进行序列搜索时,则显然会提取出周期为T1+T2的PRI固定的雷达脉冲序列,如图6所示。剩余脉冲重新进行一级直方图统计,会在骨架周期处形成唯一的峰值,序列搜索后又会分选出1部PRI等于骨架周期的雷达。因此,分选结果目标增批。
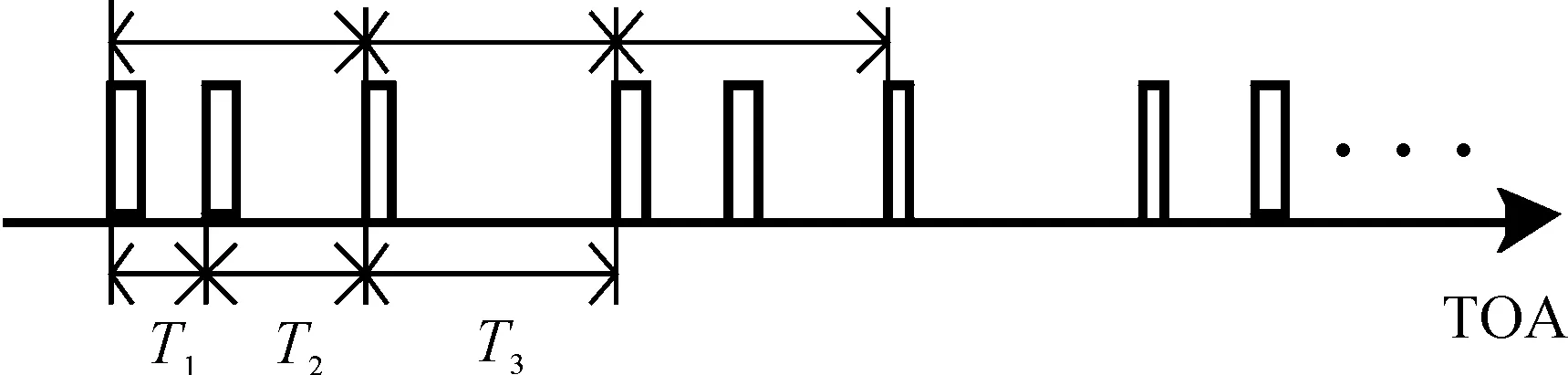
图6 3参差信号序列搜索示意图
综上分析,为破坏SDIF对3参差信号的分选性能,可以设计满足关系式(3)的子PRI。
2.34~7参差信号
对n(n≥3)参差信号的各级直方图分析,可以发现:一般情况下,m(2≤m≤n-1)级直方图会在任意m个相邻的子PRI之和处形成峰值,峰值高度几乎相同、且接近1/n倍的n级直方图峰值。因此,对于4~7参差信号,采用与3参差信号相同的分析方法,若能合理选取子PRI值,使得SDIF算法根据2~n-1级直方图峰值对应的不等于骨架周期的PRI进行序列搜索时,能搜索到脉冲序列,就会导致分选结果中目标增批。
综上,为破坏SDIF对参差信号分选性能,对4~7参差信号,要求子PRI之间呈等间隔递增关系,并且参差增量Δ(Δ>0)还需满足如下条件:
1) 4参差信号:对Δ取值无要求;
2) 5参差信号:Δ=T1/4(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列);
3) 6参差信号:Δ=2T1/3(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列);
4) 7参差信号:Δ需满足如下条件之一,即
a) Δ=3T1(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列);
b) Δ=T1/9、Δ=T1/3或Δ=T1(3级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列)。
这里需补充说明的是:① 上述抗分选设计的前提是,二级或二级以上直方图统计过程中虚假峰值能过检测门限。从理论上讲,检测门限参数某些最优取值可能会使得仅有骨架周期过检测门限。然而,实际应用中,检测门限参数都是根据经验选取的且需要适用于大部分场景,因此很难保证仅骨架周期过检测门限。换言之,上述抗分选设计的前提条件,在大多数情况下总能得到满足(参见后文仿真验证部分)。② 当PRI等间隔递减时,对PRI设计要求与上述相同(T1为最小子PRI);③ 上述PRI参差设计的核心思想是,子PRI取值保证以非骨架周期能成功进行序列搜索,从而导致分选目标增批。因此,上述设计同样适用于对抗序列搜索[11,19]、CDIF[11]等算法分选。
3 仿真验证
以雷达信号PRI分别取3参差和5参差的情况为例,对本文设计方法进行仿真验证。
仿真参数设置:观测时间20 ms,TOA测量误差为50 ns,序列搜索容差为1 μs,直方图PRI分析范围为0.1~1 000 μs,直方图统计间隔为0.5 μs。SDIF检测门限设置为[13,18]:
(4)
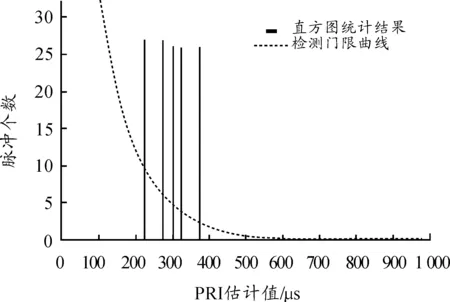
其中:τ为PRI估计值;N为脉冲总数;B为直方图上脉冲间隔的最大刻度值,即PRI分析范围的上限值;C为当前直方图级数;参数x和g为常数,并且0 考虑如下仿真场景: 场景1:3参差信号子PRI取值为T1= 50 μs,T2= 100 μs,T3= 130 μs。 场景2:3参差信号子PRI取值为T1= 50 μs,T2= 100 μs,T3= 150 μs。 场景3:5参差信号子PRI取值为T1= 100 μs,T2= 125 μs,T3= 150 μs,T4= 175 μs,T5= 200 μs。 其中,场景1下PRI不满足抗分选设计要求,场景2和场景3下PRI满足抗分选设计要求。 不同场景下的直方图统计结果见图7~图9所示。直方图统计时为避免TOA测量误差对峰值的影响,采用文献[20]中的方法对相邻直方图间隔的脉冲个数进行了合并。 图7 场景1(3参差)下二级TOA差值直方图 对于场景1,如图7所示,二级直方图在PRI估计值为150.35 μs、180.35 μs、230.35 μs处均有过门限峰值。但由于PRI不满足抗分选设计要求,按上述PRI进行序列搜索时,序列搜索不成功,不会提取出PRI不等于骨架周期的脉冲序列。进一步做3级直方图统计,可提取出骨架周期并成功进行序列搜索,剩余脉冲重新直方图统计,再进行参差分析。最终,分选现象为正确分选,分选结果有唯一目标: 目标1,PRI参差雷达,子PRI分别为50.35 μs、100.35 μs、130.35 μs。 图8 场景2(3参差)下二级TOA差值直方图 对于场景2,如图8所示,二级直方图在PRI估计值为150.35 μs、200.35 μs和250.35 μs处均有过门限峰值。由于PRI满足抗分选设计要求,分别以上述PRI值进行序列搜索时,可以成功提取出PRI为150.35μs的脉冲序列。剩余脉冲重新直方图统计,按SDIF分选流程,又以新的重复间隔提取出1个PRI固定的脉冲序列。最终,分选现象为雷达PRI类型及参数估计出错、目标增批,具体分选结果为: 目标1:PRI固定雷达,PRI为150.35 μs; 目标2:PRI固定雷达,PRI为300.35 μs。 对于场景3,如图9所示,二级直方图在PRI估计值为225.35 μs、275.35 μs、300.35 μs、325.35 μs和375.35 μs处均有过门限峰值。由于PRI满足抗分选设计要求,分别以上述PRI值进行序列搜索时,可以成功提取出PRI为375.35 μs的脉冲序列。剩余脉冲重新直方图统计,按SDIF分选流程,又提取出1个PRI参差的脉冲序列。最终,分选现象为雷达PRI类型及参数估计出错、目标增批,具体分选结果为: 目标1:PRI固定雷达,PRI为375.35 μs; 目标2:PRI参差雷达,子PRI分别为125.35 μs、325.35 μs、300.35 μs。 图9 场景3(5参差)下二级TOA差值直方图 本文提出的抗分选方法,不需要额外设计干扰脉冲,具有实现简单、更便于工程应用的优点;该方法同样适用于抗序列搜索、CDIF等算法分选。值得指出的是,在实际中,雷达参差PRI的取值很大程度上还由雷达任务性能决定,而本文主要是从抗信号分选的角度,对雷达参差PRI设计提出了定量约束。本文工作的意义在于,在不影响雷达任务性能的前提下,为如何进行一步优化PRI参数以达到射频隐身的目的提供了初步的理论参考。 [1]周一宇,安玮,郭福成,等.电子对抗原理[M].北京:电子工业出版社,2009:17-18. [2]古军峰,蓝红生,王国恩.雷达反侦察技术及战术[J].舰船电子工程,2012,32(8):71-73. [3]DAVID LYNCH,JR.射频隐身导论[M].沈玉芳译.西安:西北工业大学出版社,2009:1-13,251-413. [4]桑建华.飞行器隐身技术[M].北京:航空工业出版社,2013:259-319. [5]朱良成,张丽星,张红霞.飞行器射频隐身技术的发展与应用[J].航空科学技术,2010,21(05):11-14. [6]王文松,班晓东,龙晓波.基于抗ISODATA聚类分析的辐射源反侦察研究[J].电子信息对抗技术,2012,27(2):41-45. [7]雷武虎,戴胜波,任晓东.针对脉冲信号聚类分选的卫星电子侦察干扰技术[J].航天电子对抗,2015,31(1):21-25. [8]马力,邓杏松.捷变频技术在主动ESM对抗系统中的应用[J].舰船电子对抗技术,2014,37(6):6-9. [9]戴胜波,雷武虎,程艺喆,等.基于TOA分选的反电子侦察方法[J].电子信息对抗技术,2014,29(4):45-48. [10]徐梁昊,姜秋喜,潘继飞,等.一种抗重频分选的反侦察方法[J].四川兵工学报,2015,36(7):117-120. [11]MARDIAHK.Newtechniquesforthedeinterleavingofrepetitivesequences[J].IEEProceedings,1989,136(4):149-154. [12]MILOJEVICDJ,POPOVICBM.Improvedalgorithmforthedeinterleavingofradarpulses[J].IEEProceedings-F,1992,139(1):98-104. [13]何明浩.雷达对抗信息处理[M].北京:清华大学出版社,2010:52-58. [14]国强.雷达信号分选理论研究[M].北京:科学出版社,2010. [15]李腾.复杂重频样式雷达脉冲列的分选及识别算法[D].长沙:国防科技大学,2006,6-9. [16]曹俊纺,陈建军,孟晓琳.雷达信号分选技术研究[J].雷达与对抗,2009(1):20-22. [17]易冰歆,凌万胜.复杂电磁环境下雷达信号分选技术[J].电子信息对抗技术,2014,29(6):57-59. [18]RICHARDG.WILEY.电子情报(ELINT)——雷达信号截获与分析[M].吕跃广,译.北京:电子工业出版社,2008:240-255. [19]马晓东.雷达信号分选算法研究及硬件设计实现[D].哈尔滨:哈尔滨工程大学,2008,5-6. [20]唐永年.雷达对抗工程[M].北京:北京航空航天大学出版社,2012:287-288. (责任编辑杨继森) A Design Method of PRI Stagger Countering the SDIF Sorting Algorithm ZHANG Bao-qun (Southwest China Institute of Electronic Technology, Chengdu 610036, China) To improve the anti-sorting and anti-recognition ability of radars against electronic reconnaissance systems, a design method of PRI stagger for radar signals was proposed based on the idea of destroying the performance of sorting with the pulse repetition interval (PRI). The working process of a typical PRI sorting algorithm, the sequential difference histogram (SDIF) was analyzed, and some critical steps were discussed. It is revealed that, when the staggered PRI values are chosen properly under some contracts, the correct sorting processing can be destroyed, as a result, more than one targets appear in the sorting results. Simulation results show that, the presented design is effective during countering the signal sorting based on the SDIF, therefore it provides a preliminary theoretical guidance for the radio frequency stealth design of radar signals. anti-sorting; PRI stagger; sequential difference histogram; radar; radio frequency stealth 2016-05-02; 2016-05-25 张保群(1983—),男,博士,工程师,主要从事电子侦察、射频隐身等研究。 10.11809/scbgxb2016.09.021 format:ZHANG Bao-qun.A Design Method of PRI Stagger Countering the SDIF Sorting Algorithm[J].Journal of Ordnance Equipment Engineering,2016(9):87-91. TN973 A 2096-2304(2016)09-0087-06 本文引用格式:张保群.一种抗SDIF分选的脉冲重复间隔参差设计方法[J].兵器装备工程学报,2016(9):87-91.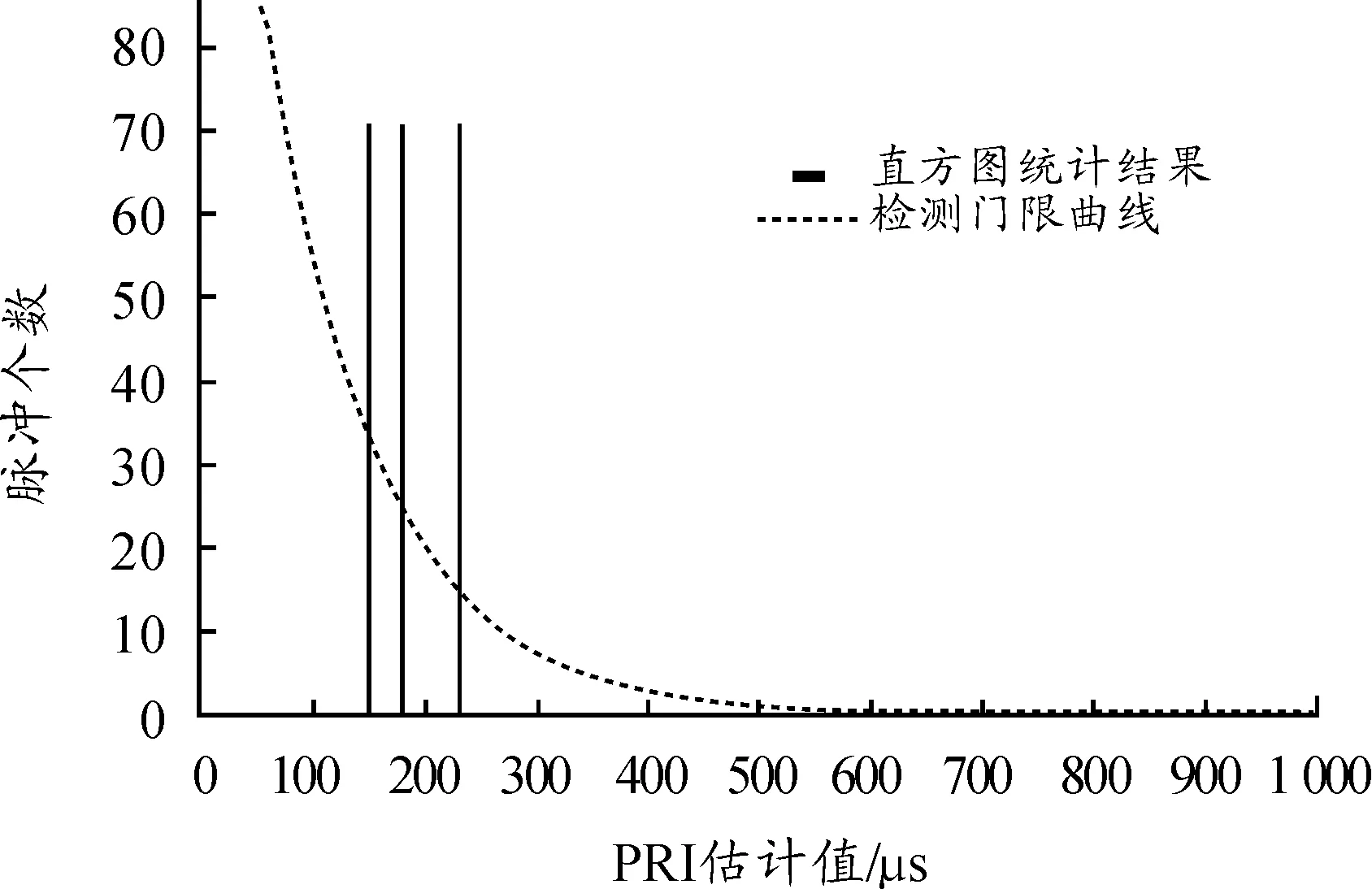

4 结论

