火炮弹丸底凹结构流场仿真及其减阻机理分析

陆海波，崔国亮，张海涛，马　强

(南京炮兵学院 自行火炮系，南京　211132)



【装备理论与装备技术】

火炮弹丸底凹结构流场仿真及其减阻机理分析

陆海波，崔国亮，张海涛，马强

(南京炮兵学院 自行火炮系，南京211132)

针对火炮弹丸底凹结构的减阻效果展开研究，基于N-S方程求解，得到了底凹弹弹丸在超声速流场条件下的绕流流场参数分布以及弹丸的气动阻力，讨论了不同底凹深度对弹丸流场、减阻效果的影响，分析了底凹结构减阻机理；研究发现：位于弹丸底部的回流流动对底凹结构的减阻效果起决定性作用；在超声速条件下，底凹结构越深，底凹弹气动阻力越小。

底凹弹丸；减阻；超声速；数值模拟

目前，针对削弱弹丸底阻的弹药增程技术主要有底凹与底排[3]两种。底凹弹是指底部带有凹窝的旋转稳定式炮弹[4]，由美军于上世纪60年代最先开始研制。研究表明底凹结构是一种有效的削弱弹丸底阻的方法[5-6]。底凹弹可提高弹丸的射程、威力和精度。设计试验表明，在相同条件下，底凹弹可增程3%～5%，如进一步在底部开侧向孔的情况下，可增程10%～12%[7]。

早期针对底凹结构的研究以试验为主，受当时条件限制，理论分析也多使用工程方法。近年来，出现了一些针对底凹结构流场的数值分析，比如鞠玉涛等[8]数值模拟了圆柱弹与底凹弹形的绕流流场，得到了流场的宏观结构以及底部涡流结果的变化规律。王芳等[9]采用Fluent软件研究了底凹装置对弹丸阻力系数的影响，得出了在亚声速条件下，增大底凹深度能增大减阻效果，但底凹深度有一最佳值。对于底凹弹在超声速流动条件下的数值分析却不多见。

本文针对底凹减阻技术，基于大、中口径远程压制火炮弹丸飞行多处于超声速条件的现实，对超声速条件下底凹弹的绕流流场展开数值仿真，分析了底凹结构减阻效果的形成机理，探讨了底凹深度对减阻效果的影响，为下一代底凹弹的设计提供研究与理论储备。

1　结构示意与算例安排

底凹弹底凹深度的选择需要从减阻效果、弹丸装药量、飞行稳定性等多个方面考量。本文分析底凹结构的减阻机理，讨论底凹结构不同深度对弹丸的超声速绕流流场以及阻力的影响，得出深度变化对弹丸阻力的影响趋势，设置了多个底凹深度的算例，甚至包含在实际弹丸设计中不可能考虑的极限深度。弹丸外形结构示意图如图1所示。不同底凹深度具体算例如表1所示。

图1　算例结构示意图

算例标号底凹深度/mm算例标号底凹深度/mm算例120算例4120算例240算例5200算例380算例6300

2　数值方法

2.1控制方程及离散

基于火炮弹丸绕流流场的轴对称特性，使用可压缩的轴对称N-S方程为控制方程[10]:

(1)

式(1)中，x为流向，r为径向。U=[ρ,ρu,ρv,e]T，E=[ρu,ρu2+p,ρuv,u(e+p)]T，F=[ρv,ρuv,ρv2+p,v(e+p)]T，S=[ρv,ρuv,ρv2,v(e+p)]T，Ev=[0,τxx,τxr,qx]T，Fv=[0,τrx,τrr,qr]T，H=[0,τrx,τrr,qr]T，e=ρ[CvT+(u2+v2)/2]，τ为剪切应力，q为热通量，ρ，u，v，T，p，e分别为流体的密度，轴向速度，径向速度，温度，压力以及单位质量流体的能量。

由图7可知，在培养的鲁氏酵母菌周围的琼脂未显示绿色，同时并未出现透明圈，说明没有产生α-溶血和β-溶血现象，而金黄色葡萄球菌周围则显示透明溶血圈；实验结果说明，本试验所用的鲁氏酵母菌无溶血现象发生，说明菌株不是溶血细菌，具有食用安全性。

结合k-ε湍流模型[11]进行方程求解。对流通量采用Van Leer格式处理，黏性扩散项采用2阶中心差分格式，时间项采用LU-SSOR的隐式格式离散分解。

2.2网格生成

使用Poisson方程生成贴体网格[12]

(2)

式(2)中：(x,y)为物理平面坐标；(ξ,η)为计算平面坐标；P，Q为控制网格疏密的源项[13]。

计算模型网格(以底凹深度40mm为例)如图2所示。

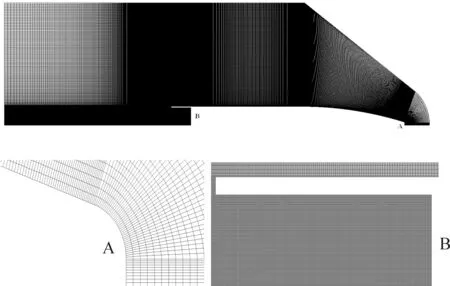
图2　计算网格

2.3边界条件与数值假设

来流边界条件如表2所示。计算中认为壁面无滑移并且使用了绝热壁假设。

表2　来流边界条件

3　结果与分析

3.1流场参数分布

图3～图5分别给出了各算例绕流流场的流线和马赫数、温度以及压力分布情况。

由于超声速流动后方扰动无法向前传递，底凹结构的影响主要集中于弹丸的尾部流场。由各图亦可见，各算例的弹丸的前部流场是一致的，主要变化在尾部流场。

图3为各算例流场流线及马赫数分布。由图可知，弹丸头部的脱体弓形激波波后存在相对低速流动区域，但是来流速度并没有跌入亚声速。进入弹尾，流动急剧扩张形成了一个高速膨胀区。在弹丸的底部，都形成了回流区，回流都延伸到底凹结构内部。随底凹深度加大，回流区域进一步向底凹深处扩张。

图4为流场压力等值线分布，由图可见清晰的弹丸侧后方的膨胀低压区。由于底凹结构的存在，使得底部回流有了“充分发展”的空间，在底凹结构内部弹丸的底面上出现了相对高压。由流线图(图3)，弹丸底凹底面存在两个“停滞点”，底凹中心以及底面与侧壁的交点，所以压力分布也表现为两个局部高压中心，其局部放大如图5所示(以算例1为例)。

图3　各算例马赫数及流线分布

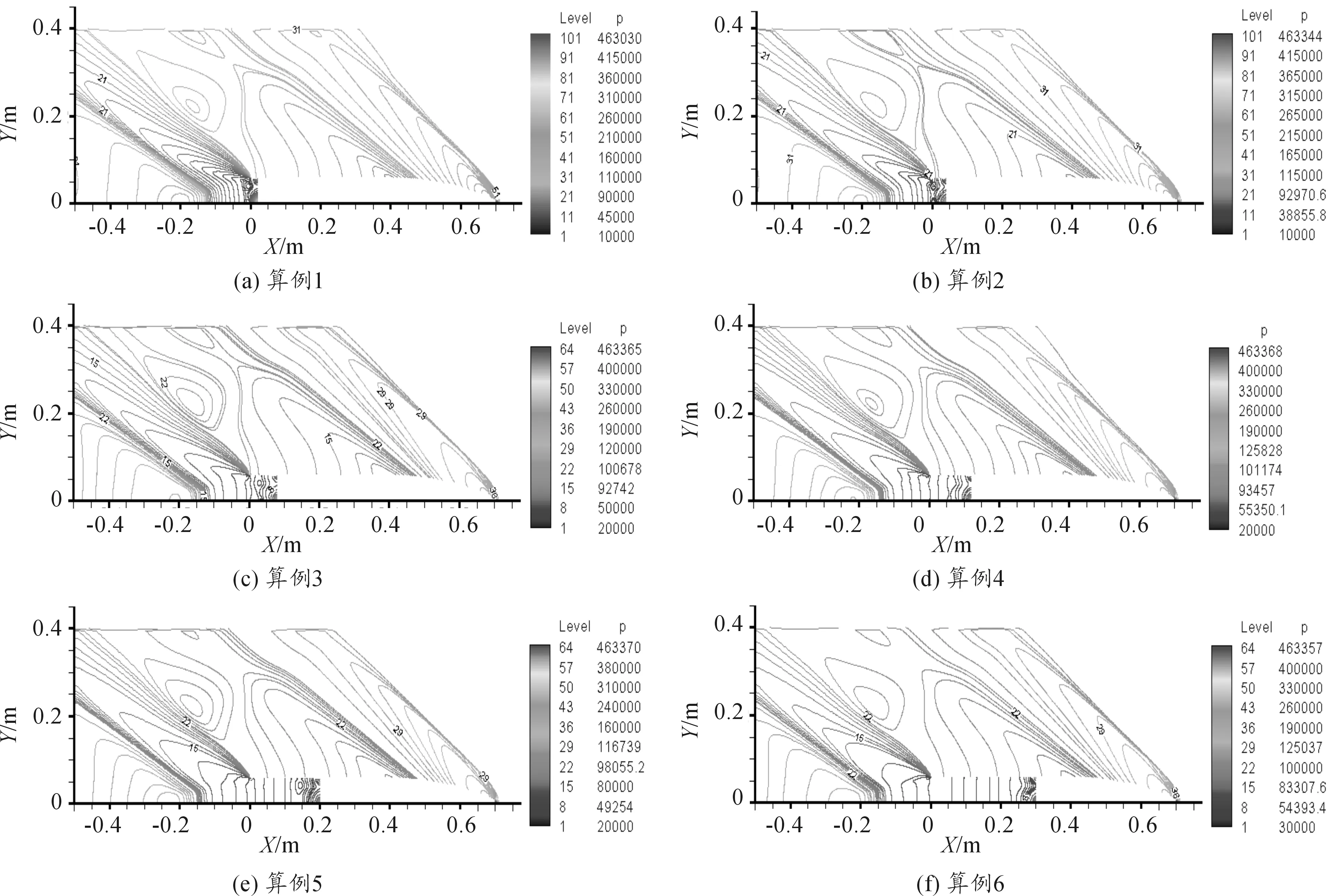
图4　各算例压力分布

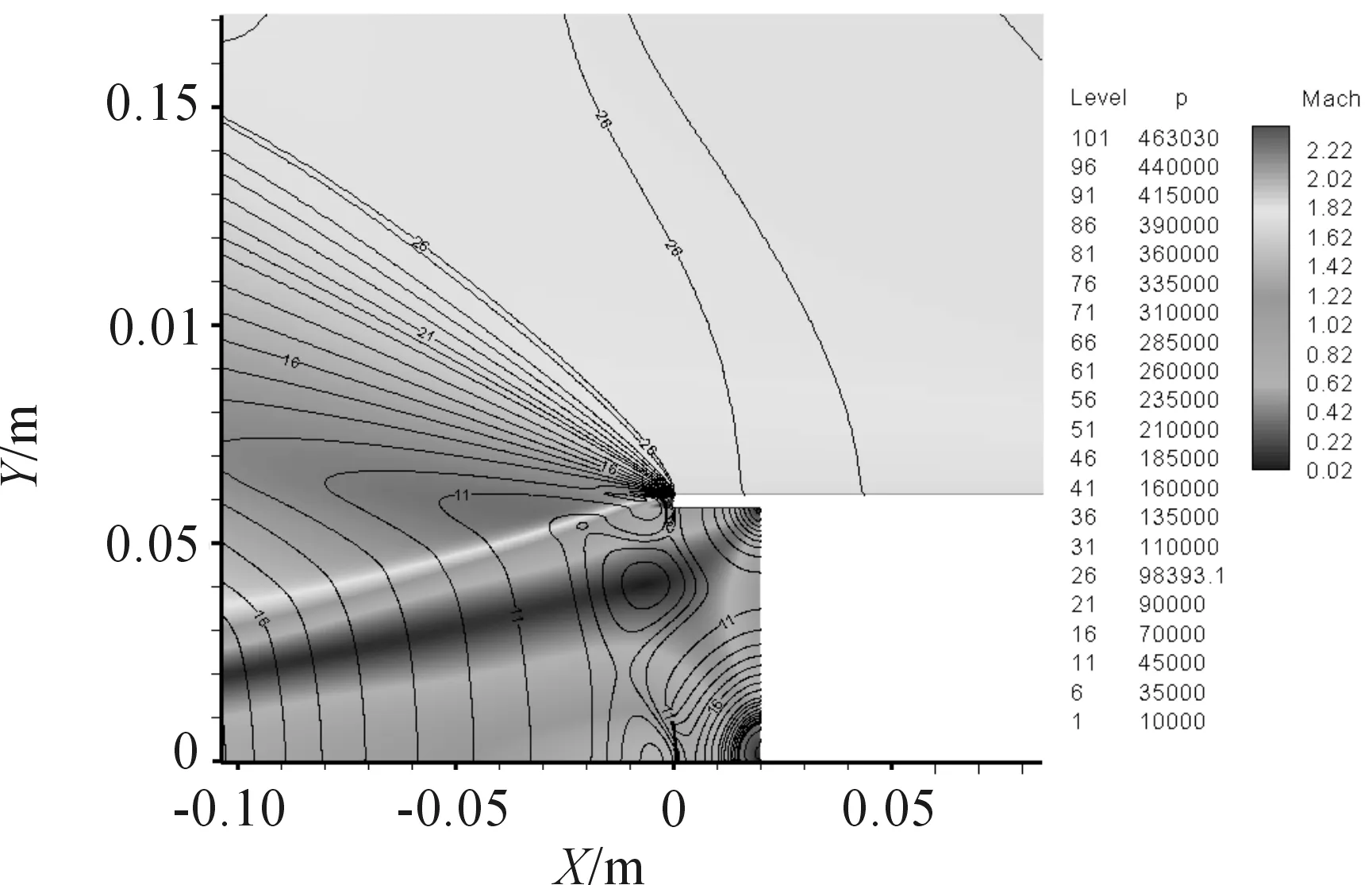
图5　底部马赫数与压力分布的局部放大(算例1)

3.2气动受力的变化

弹丸气动阻力系数(Cd)计算式如下：

(3)

式(3)中，Fd为气动阻力，ρ∞为来流密度，u∞为来流速率，Sref为参考面积(弹丸横截面积)。

图6给出了不同底凹深度的各算例气动阻力系数。由图可见，随着底凹深度增加，弹丸的气动阻力持续下降。

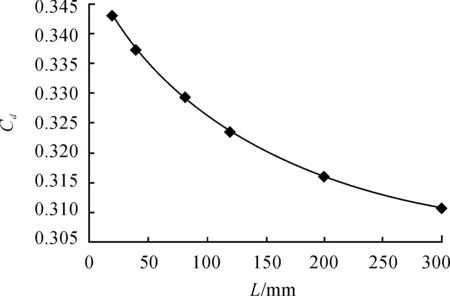
图6　气动阻力系数变化

图7给出了各个算例凹腔底面的压力分布与对应底面面积的示意。由图可知，随着底凹深度增加，弹丸底面压力呈规律性变化，不同底凹深度弹丸的底面压力曲线存在两个高低相对变化交点。在凹腔底面的中心部分(图7中面积示意的“A”部分)，浅的底凹底面具有更大的压力，在径向大约17.8mm处，这一趋势发生改变，深的底凹底面上压力更大，直至径向53.8mm左右，再向外(图7中面积示意的“C”部分)，浅的凹腔底面压力重新取得优势。由这一分布规律可知，对于更深的底凹结构，在凹腔内的两个流动“停滞点”(如图4)，其压力较低，但是在两个流动“停滞点”之间的区域，深的凹腔有优势。

由图7的面积示意亦可见，“B”部分的面积远远大于“A”与“C”之和，所以“B”区范围内的压力分布在弹丸整个底压中，占主导地位。所以不同深度底凹弹丸气动阻力上的表象与底面“B”区压力的表象一致：深的底凹弹底面“B”区上压力更大，弹丸的总体气动阻力更小。

此外还需要说明的是，底凹结构侧壁是有厚度的，其对应的弹尾底面圆环也是弹丸底面的一部分。但是由于其面积非常小，更主要的是该圆环处于弹体侧面向弹底的转折处，气流在此发生急剧膨胀，此圆环上的底面压力远远小于底凹结构底面的压力，所以在此没有对这一部分进行详细分析。

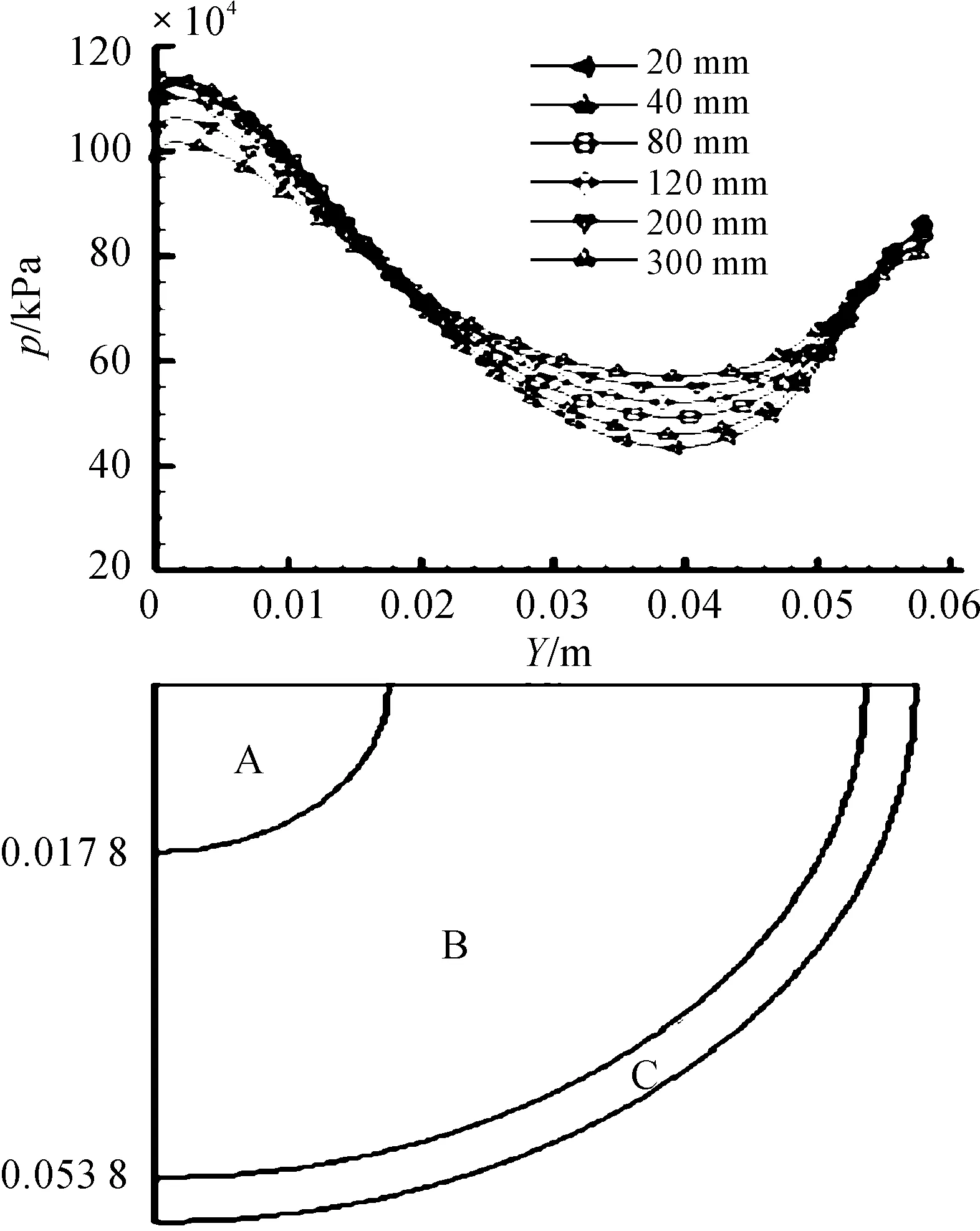
图7　各算例弹丸底面压力分布与面积示意

4　结论

以数值模拟为主要研究手段，对火炮底凹弹弹丸的底凹结构减阻性能展开研究。位于弹丸底部的回流流动对底凹结构的减阻效果起决定性作用。在不考虑弹丸装药量、飞行稳定性等其它火炮弹丸外形设计因素的条件下，仅仅从底凹结构减阻的角度出发，凹腔设计越深越好。在本文计算范围内，弹丸的飞行阻力随底凹结构的深度增加而减小。随着底凹结构的深度增加，在弹丸后部由流体的粘性以及逆压而产生的回流需途经更久的路程到达靠近底凹底面的位置，回流速度衰减更多，压力得到恢复和提高。从而导致随着底凹深度的增加，弹丸底面压力总体上升，弹丸所受气动阻力下降。

[1]王中原.超声速底凹弹侧壁开孔对飞行阻力的影响[J].空气动力学学报,1997,15(4):502-506.

[2]浦发,王中原．减阻增程的潜力及其可能途径的分析[J].弹道学报,1986(3):38-42.

[3]谢利平,史金光,李元生.底排参数对底部排气弹弹道特性的影响[J].兵器装备工程学报，2016,37(1):34-39.

[4]李向东,钱建平,曹兵．弹药概论[M].北京：国防工业出版社,2004:29-31．

[5]HOWELL,SIMS-WILLIAMS D,SPROT A,et al.Bluff Boby Drag Reduction with Ventilated Base Cavities[J].SAE Technical Papers,2012,5(5):152-160.

[6]IBRAHIM A,FILIPPONE A.Supersonic Aerodynamics of a Projectile with Slot Cavities[J].Aeronautical Journal,2010,114(1):15-24.

[7]华恭,欧林尔.弹丸作用和设计理论[M].北京：国防工业出版社,1975.

[8]鞠玉涛,周长省,李坚．底凹弹绕流流场波谱规律数值分析[J].弹箭与制导学报,2003,23(3):144-146.

[9]王芳,郎田,魏志芳.底凹装置对弹丸阻力系数的影响[J].兵工自动化， 2014,33(11):1-4.

[10]王承尧,王正华,杨晓辉．计算流体力学及其并行算法[M].长沙：国防科大出版社,2000.

[11]陶文铨.数值传热学[M].2版.西安：西安交通大学出版社,2001.

[12]BAKER A J.Numercal Grid Generation Techniques [R].NASA CP-2166,1980.

[13]THOMAS P D,MIDDELCOFF J F.Direct Control of the Grid Point Distribution in Meshes Generated by Elliptic Equations[R].AIAA-83-0037,1983.

(责任编辑周江川)

Flow Field Simulation and Drag Reducing Mechanism Analysis of Projectile with Base Cavity

LU Hai-bo, CUI Guo-liang, ZHANG Hai-tao, MA Qiang

(Department of Self-Propelled Gun, Nanjing Artillery Academy, Nanjing 211132, China)

The drag reducing effect of projectile with base cavity was investigated numerically. Based on the solving of the Navier-Stokes (N-S) equations, the distributions of the flow field parameters and the aerodynamic drag were obtained. The effect of the base cavity length on the flow field and the drag reducing were discussed. The results show that the recirculation region plays a pivotal role for the reduction of the drag. Under the condition of supersonic, the deeper the bottom concave structure, the bottom concave playing the aerodynamic drag is smaller.

projectile with base cavity; drag reducing; supersonic; numerical simulation

2016-04-05；

2016-05-26

陆海波(1980—)，男，博士，讲师，主要从事高速飞行器气动力、热分析与控制研究。

10.11809/scbgxb2016.09.001

format:LU Hai-bo, CUI Guo-liang, ZHANG Hai-tao, et al.Flow Field Simulation and Drag Reducing Mechanism Analysis of Projectile with Base Cavity[J].Journal of Ordnance Equipment Engineering,2016(9):1-4.

TJ012

A

2096-2304(2016)09-0001-05

本文引用格式：陆海波，崔国亮，张海涛，等.火炮弹丸底凹结构流场仿真及其减阻机理分析[J].兵器装备工程学报，2016(9):1-4.