多蛋交接耐压壳仿生研究

张　建　左新龙　王纬波　唐文献

1.江苏科技大学，镇江,212000　　2.中国船舶科学研究中心，无锡,214082



多蛋交接耐压壳仿生研究

张建1,2左新龙1王纬波2唐文献1

1.江苏科技大学，镇江,2120002.中国船舶科学研究中心，无锡,214082

以鹅蛋壳为生物原型，开展了多蛋交接耐压壳仿生设计及性能研究工作。首先，通过蛋壳生物学试验，建立了蛋形函数；其次，对深海多蛋交接耐压壳进行设计，建立了蛋壳个数分别为2、3、4、5、6的数值模型，研究其临界屈曲载荷、极限强度载荷和储备浮力特性；最后，通过正交试验设计，分析了多蛋交接耐压壳主要几何参数对其性能的影响规律。结果表明：Kitching蛋形函数与鹅蛋经线的吻合程度最高，其长轴与偏心距之比取45，蛋形系数取0.69；深海多蛋交接耐压壳的临界屈曲载荷远大于极限强度载荷，即极限强度载荷为结构设计的主要因素；蛋形壳个数对极限强度载荷和浮力系数影响很小；蛋形壳厚度对极限强度载荷和浮力系数影响较大；加强肋对浮力系数影响较小，而对极限强度载荷影响较大。

耐压壳；多蛋交接；蛋形函数；仿生设计

0　引言

潜水器是大洋勘查与深海科学研究的重要装备，作为潜水器的重要组成部分，耐压壳起着保障下潜过程中内部设备正常工作和人员健康安全的作用，其质量占潜水器总重的1/4～1/2。耐压壳的设计对潜水器安全性、机动性、空间利用率和人机环等性能具有重要影响[1-2]。

现役的深海耐压壳多为单球形，少数为多球交接结构[3-4]。Pan等[5]对比分析了现有深水球形耐压壳的设计规范，通过原型试验和非线性有限元分析，建立了预测深海钛合金球形壳极限强度的经验公式。苟鹏等[6]对多球交接耐压壳的结构优化问题作了研究，总结了双球交接耐压壳的两种典型破坏模式，提出了三种新的多球交接形式。Liang等[7]采用EIPF(extended interior penalty)和DFP(Davidon-Fletcher -Powell)方法，研究了多球壳连接的大深度潜水器耐压壳体的优化设计问题。但这些结构无法最优协调潜水器的安全性、机动性、空间利用率和人机环等特性。例如，对于单球形耐压装备，在实际受载过程中，由于对缺陷非常敏感，发生失稳时的压力仅为理论值的1/4～1/3[8]，安全性较差；单球形耐压装备只能依靠增大球半径来增大内部空间，但半径的增大会导致水阻力增大，降低潜水器的机动性；球形耐压装备曲率较小且处处相等，导致内部设备布置困难，空间利用率较低，人员舒适性差，进而降低潜水器的人机环特性。多球形耐压装备在一定程度上扩大了舱室空间，提高了人员舒适性，但仍然无法克服缺陷敏感度高、空间利用率低等缺点[9-10]。

蛋壳满足圆顶原理，具有超强的耐压特性，是一种优异的耐压壳仿生设计原型。蛋形耐压壳体使得潜水器的安全性、流体动力学特性、空间利用率、人机环最优协调成为可能[11-14]。张建[15]研究了千米水深蛋壳仿生耐压壳的设计理论与分析方法，设计了6 km水深鸡蛋壳、鹅蛋壳仿生耐压壳，并从储备浮力、壳内空间利用率、流线型、乘员舒适性等方面进行综合比较，得到鹅蛋壳仿生耐压壳可为深水耐压设计提供有效参考的结论；在此基础上，进一步研究了复合材料蛋形耐压壳的力学特性，通过理论计算，证明了蛋形耐压壳综合性能优于球形耐压壳综合性能，可最优协调强度稳定性、浮力系数、空间利用率、人机环特性以及水动力学特性，且对缺陷敏感性低，便于开孔、开窗，在深海潜水器上具有良好的应用前景[16]。然而，对于单蛋形耐压壳结构的潜水器，其单舱室空间较小，无法满足深海潜水器开发的要求，尤其是深海空间站。多蛋交接耐压结构继承了单一蛋形结构的缺陷敏感度低、安全性高、空间利用率高、人机环特性好等优点，可在不降低安全性的前提下去除曲率较大的端部，用于开孔连接、开设舱门和观察窗，进一步提高空间利用率。此外，采用多个蛋形结构相连的方案，可进一步扩大舱室空间，提高人机环特性，同时也便于分段制造。采用不同大小蛋形壳体相连的方案，也便于具有流线型轻外壳的布置，减小潜水器流体阻力，提高潜水器的流体动力学特性[17]。

本文开展多蛋交接耐压壳仿生设计及性能研究工作。首先，基于蛋壳生物学试验建立蛋形函数，在此基础上，设计多蛋交接耐压壳结构；接着，建立蛋壳个数分别为2、3、4、5、6的数值模型，研究其临界屈曲载荷、极限强度载荷和储备浮力特性；最后，通过正交试验设计，分析多蛋交接耐压壳主要几何参数对其性能的影响规律，并给出不同参数组合，避免参数的盲选和反复试验。

1　蛋壳生物学试验及结果分析

1.1蛋形系数统计分析

蛋形系数为蛋壳短轴(B)与长轴(L)之比(图1)，是描述蛋壳几何特征的重要参数。选取204个鹅蛋(品种为浙江江山白鹅，鹅龄为1～2年)，使用游标卡尺(型号为530-118/114，量程为0～200 mm，精度为0.01 mm)采集蛋壳的短轴与长轴值。运用线性回归分析(SPSS)进行统计描述，获得蛋形系数的P-P图，如图2所示。经分析，认为蛋形系数为正态分布，其均值为0.69，偏度为-0.01，峰度为2.9。因此，在仿生鹅蛋壳时，作为优选，蛋形系数取0.69。

图1　鹅蛋长短轴

图2　蛋形系数P-P图

1.2蛋壳三维扫描试验

选取10个鹅蛋，通过ATOSⅡ光学扫描仪(单幅测量范围为500 mm×300 mm；CCD相机像素为2×2M，分辨率为1624像素×1236像素)获得其三维模型。随机选取沿蛋壳长轴的三条蛋经线，其所在面夹角互为120°，计算得到三条蛋壳经线的相互皮尔逊相关系数(PPMCC)，如表1所示。可见，三条蛋壳经线的相互皮尔逊相关系数均大于0.99，可认为蛋壳是高度对称的旋转壳。因此，在仿生鹅蛋壳时，可仅选用一条蛋壳经线作为研究对象。

表1　三条蛋壳经线的相互皮尔逊相关系数

1.3蛋形函数选取

蛋形函数是仿生蛋壳不可或缺的部分。现有蛋形函数方程有Kitching蛋形函数[18]、Brandt蛋形函数[19]以及N-R蛋形函数[20]，分别如下所示：

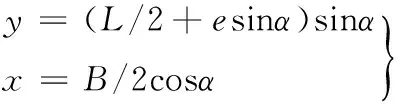
(1)

(2)

(3)式中，e为偏心距(蛋壳质心与长轴中心的距离)；α为点(x，y)和原点的连线与x轴的夹角；β为平面曲率参数,β∈[0,1]。

三种蛋形函数曲线分别如图3、图4、图5所示。

图3　Kitching蛋形图

图4　Brandt蛋形图

图5　N-R蛋形图

运用ORIGIN软件，求得一条蛋经线分别与3种蛋形函数曲线的皮尔逊相关系数，如表2所示。可见，Kitching蛋形函数曲线与蛋经线的皮尔逊相关系数为0.9989，吻合程度最高。试验鹅蛋壳长轴L与偏心距e之比的均值为45。因此，在仿生鹅蛋壳时，作为优选，蛋形函数选用Kitching函数方程，取L/e=45。

表2　蛋经线与蛋形函数曲线的皮尔逊相关系数

2　多蛋交接耐压壳的设计与建模

蛋形函数选用Kitching蛋形函数，取B/L=0.69，L/e=45。多蛋交接耐压壳包括若干个蛋形仿生壳，相邻蛋形壳的钝端和尖端通过环形肋顺次连接(图6)。多蛋交接的耐压壳艏部为蛋形壳的钝端，如图6左端所示，其尾部为蛋形壳的尖端，如图6右端所示。主要几何参数包括：交接蛋形壳的个数n、仿生蛋形壳长轴L、加强肋厚度 h、加强肋宽度b、加强肋半径a和仿生蛋形壳厚度t(图6)。

图6　三蛋形壳截面

运用HYPERMESH将多蛋交接耐压结构的每个蛋形壳等分成6块进行网格划分，以消除网格大小不同对软件分析的影响，单元类型为线性四边形单元S4。图7所示为交接个数分别为2、3、4、5、6的网格模型。利用有限元软件ABAQUS对多蛋交接耐压结构进行临界屈曲载荷和极限强度载荷分析。多蛋交接耐压装置在深水受均布压力时，不受任何约束，为了消除模型的刚性位移，选择三个点限制耐压装置的6个方向位移。该约束为虚约束，三个点的滞反力都为0，说明该约束完全不影响分析结果。本文选用的蛋形壳材料为Ti-6Al-4V(Tc4)，许用应力为830MPa，弹性模量为110GPa，泊松比为0.3，密度为4.5g/cm3。

图7　多蛋交接耐压壳的网格模型

浮力系数f是评价潜水器性能的重要指标，其表征着潜水器的运载能力，可由下式计算：

(4)

式中，V1为多蛋交接耐压壳体积(排水量)；V2为多蛋交接耐压壳的材料体积；ρ1为海水密度，ρ1=1.025g/cm3；ρ2为Ti-6Al-4V(Tc4)密度，ρ2=4.5g/cm3。

3　结果分析与讨论

3.1蛋形壳个数影响规律分析

分别设计交接个数为2、3、4、5、6多蛋交接的模型，主要几何参数如下：L=2.4m、h=100mm、b=60mm、a=500mm、t=60mm。利用ABAQUS软件对模型求解，获得不同交接个数下的临界屈曲载荷、极限强度载荷和浮力系数，如表3所示。可见，双蛋耐压壳的极限强度载荷最大，三蛋形壳极限强度载荷最小。当交接个数不小于4时，极限强度载荷随交接个数增大而逐渐减小，变化幅度仅为0.05%。浮力系数随交接个数增大逐渐减小，并趋近于单个蛋形壳的浮力系数，变化幅度仅为3.9%。因此，蛋形壳个数对极限强度载荷和浮力系数影响很小。

表3多蛋壳交接临界屈曲/极限强度/浮力系数对比表

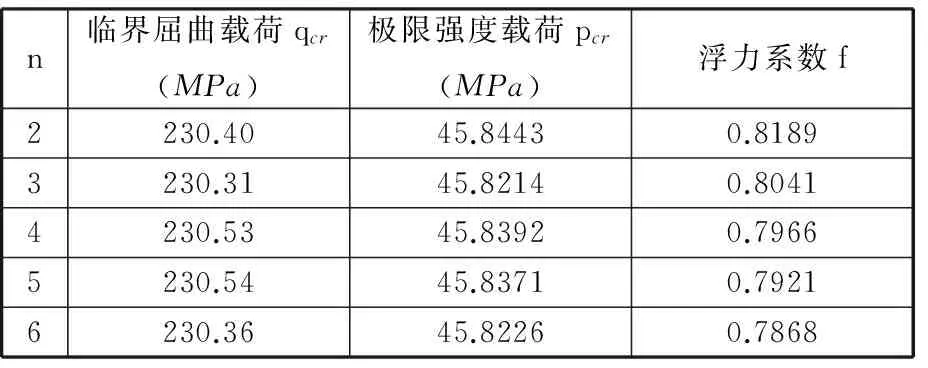
n临界屈曲载荷qcr(MPa)极限强度载荷pcr(MPa)浮力系数f2230.4045.84430.81893230.3145.82140.80414230.5345.83920.79665230.5445.83710.79216230.3645.82260.7868

此外，多蛋交接耐压壳的临界屈曲载荷远大于极限强度载荷，即极限强度载荷为结构设计的主要因素，所以在研究分析时可以忽略临界屈曲载荷对多蛋壳结构设计的影响。图8是交接个数分别为2、3、4、5、6多蛋交接模型的屈曲模态，可以看出，多蛋交接耐压壳失稳均发生在交接环肋处，且交接的个数对失稳模式并无影响。综上，可将分析模型简化为三蛋形壳，从而极大地减小了模型和正交试验设计的复杂程度。

(a)n=2　　　　　(b)n=3(c)n=4

(d)n=5　　　　　　(e)n=6　图8　多蛋交接耐压壳屈曲模态

3.2主要几何参数对多蛋交接耐压壳结构性能的影响

多蛋交接耐压壳的主要参数包括仿生蛋壳长轴长度L、加强肋厚度 h、加强肋宽度b、加强肋半径a和仿生蛋壳厚度t。它们决定着多蛋交接耐压壳的几何形状，其因素水平如表4所示。采用正交表L27(35)设计试验，试验方案和结果如表5所示。

表4　正交试验设计各因素水平表

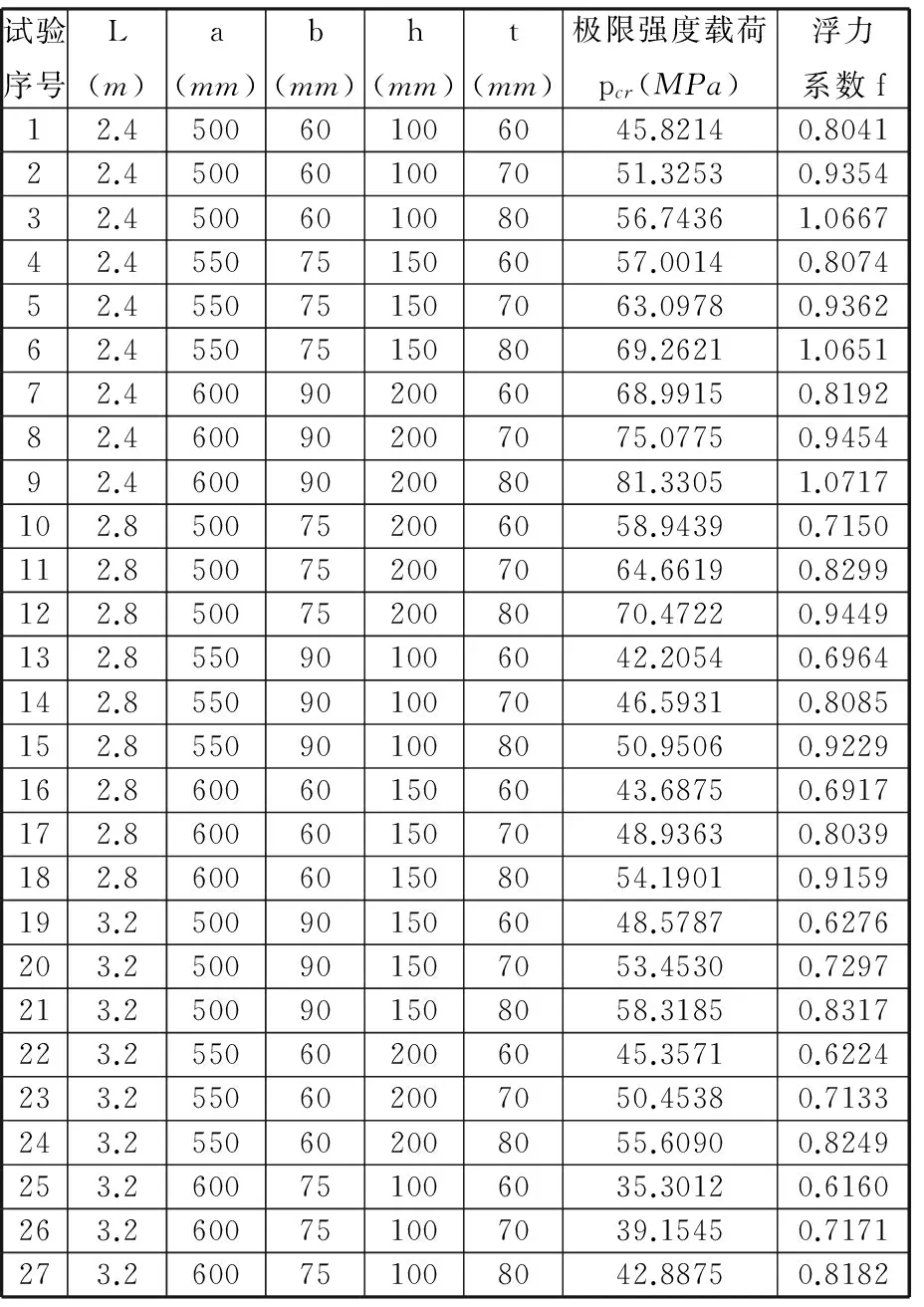
表5　正交试验表

Minitab是现代质量管理统计软件，作为一款优异的正交试验后处理软件，可有效地分析各因素各水平对性能指标的均值主效应、信噪比主效应和贡献率。其中，均值主效应的幅值越大，对性能指标影响越重要；信噪比为质量特征值的均值与样本方差比值的平方，反映稳健设计中性能指标稳健程度，其数值越大，系统波动越小，越稳定；贡献率为各因素的均值主效应幅值占整体幅值的百分比，可衡量各因素对性能指标影响的程度。运用Minitab软件对正交试验结果进行统计分析，可获得各因素各水平对极限强度载荷和浮力系数的均值主效应、信噪比主效应和贡献率，如图9、图10所示。

(a)各因素水平对极限强度载荷均值主效应

(b)各因素水平对极限强度载荷信噪比主效应

(c)各因素水平对极限强度载荷贡献率图9　各因素对极限强度载荷影响

(a)各因素水平对浮力系数均值主效应

(b)各因素水平对浮力系数信噪比主效应

(c)各因素水平对浮力系数贡献率图10　各因素对浮力系数影响

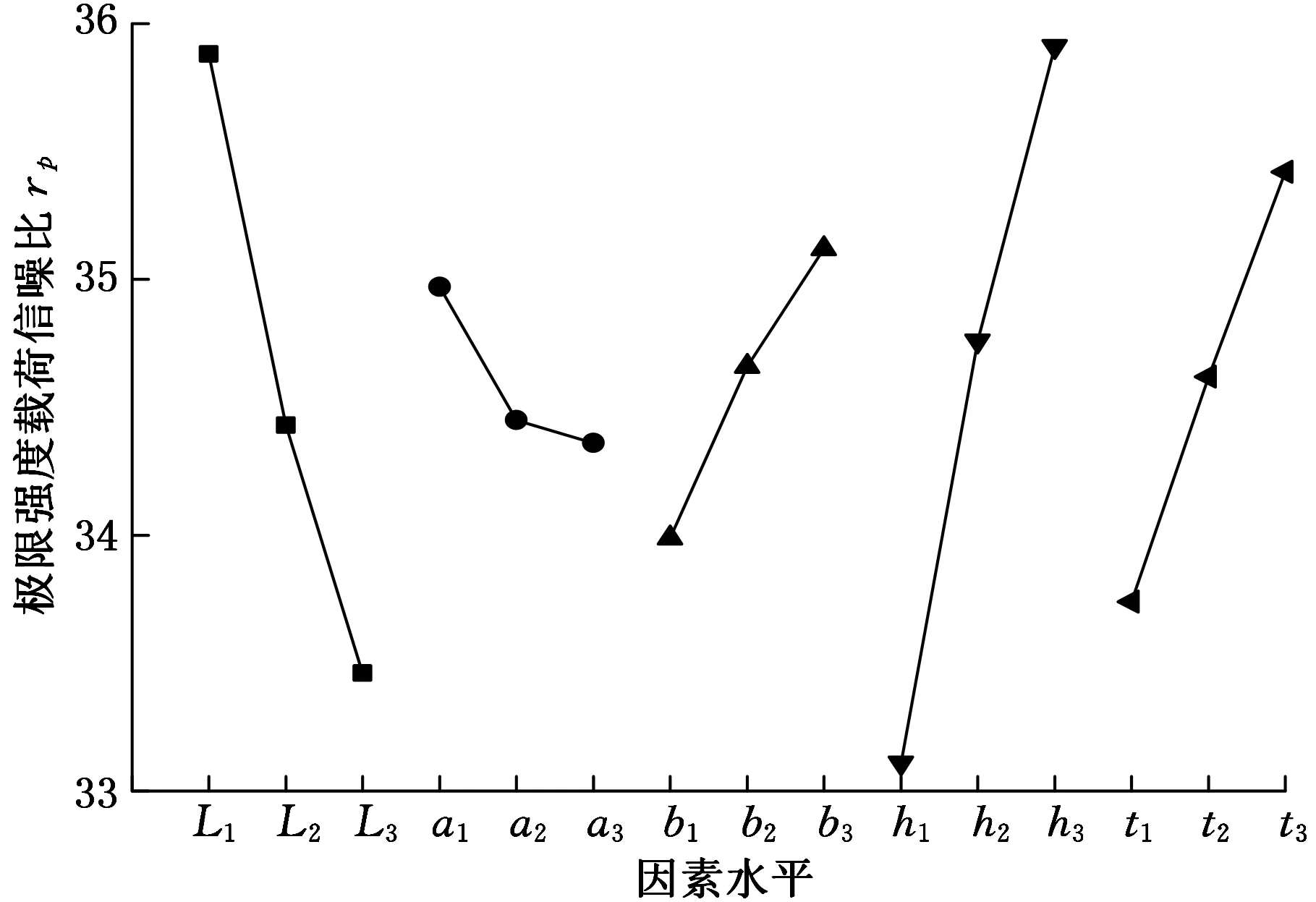
由图9a、图9c可以看出，加强肋厚度h、仿生蛋壳长轴长度L、仿生蛋壳厚度t 、加强肋宽度b、加强肋半径a对三蛋形壳的极限强度载荷影响依次减弱； h、L对极限强度载荷的影响为主导因素。b、h、t的值越大，极限强度载荷越大；L的值越大，极限强度载荷反而越小；a的值越大，极限强度载荷呈减小再增大趋势，但对极限强度载荷的总贡献率为负；由图9b可以得到主次因素顺序的最优组合为h3-L1-t3-b3-a1，以获得最大的极限强度载荷。

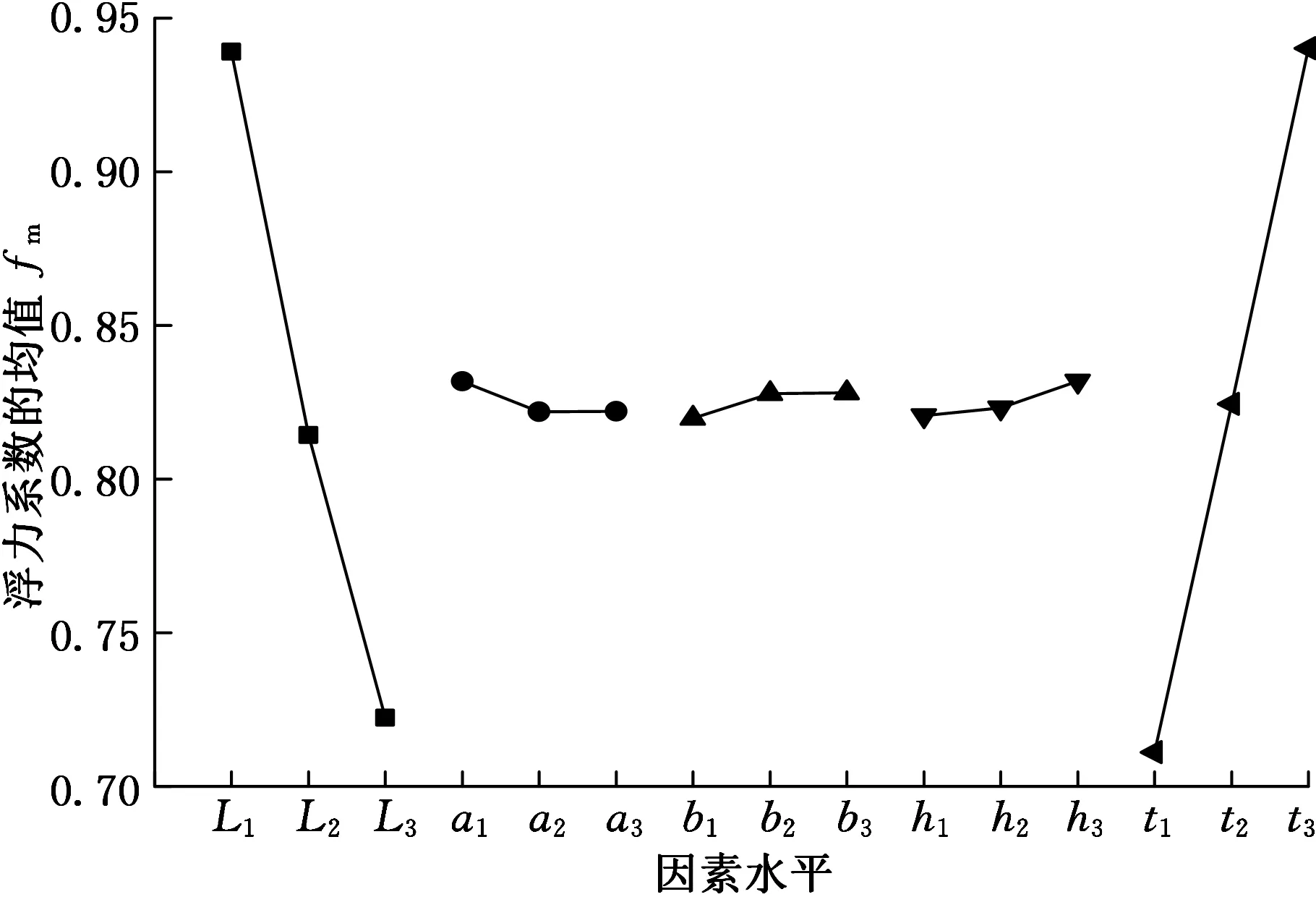
由图10a、图10c可以看出，仿生蛋壳厚度t、仿生蛋壳长轴长度L、加强肋厚度h、加强肋半径a、加强肋宽度b对三蛋形壳的浮力系数影响依次减弱；t、L对浮力系数影响为绝对主导因素，其他参数对浮力系数影响极小；L、a的值越大浮力系数越小；t、h和a的值越大浮力系数越大。由图10b可以得到主次因素顺序的最优组合为t1-L3-h1-a3-b1，以获得最小的浮力系数。

极限强度载荷与浮力系数的最优组合并不相同，需要综合考虑二者指标，最终获得影响因素的排序和优异组合。耐压结构在实际设计中应优先考虑下潜深度，保证安全性，即优先考虑其极限强度载荷。加强肋厚度h在对极限强度载荷影响中为主导因素，而对浮力系数影响较小，可在不用考虑对浮力系数影响下，增大h，提高极限强度载荷。因此，可将h作为影响极限强度载荷和浮力系数综合指标的第一主要因素。极限强度载荷与浮力系数的最优组合为h3-L1-t3-b3-a1和t1-L3-h1-a3-b1，L均为第二主要因素，且t和L对浮力系数影响不相伯仲，而t对极限强度载荷影响要小于L。因此， L和t可分别作为影响极限强度载荷和浮力系数综合指标的第二、第三主要因素。a、b对浮力系数影响甚微，可按其对极限强度载荷的影响主次划分。最终，获得主要参数的影响排序和优异组合为h3-L-t1-b-a。确定h和t后，基于正交表L27(35)设计的试验组，可确定试验序号7、10、22三组为优异组合。

根据强度载荷公式[16，21]：

pcr=KρgH/0.9

(5)

式中，K为安全系数，取1.5；ρ为海水密度，取1.025g/cm3；g为重力加速度，g取9.8m/s2；H为水深。

可以将三组优异组合划分为适用于不同水深的参数组合。试验序号22的参数组合为h3-L3-t1-b3-a2，适用于3000～4000m水深；试验序号10的参数组合为h3-L2-t1-b2-a1，适用于4000～5000m水深。试验序号7的参数组合为h3-L1-t1-b3-a3，适用于5000～6000m水深。三组试验参数的组合并非为三蛋交接耐压壳的最优组合，但其参数组合可为深海三蛋交接耐压壳仿生设计提供参考依据，避免参数的盲选和反复试验。此外，蛋形壳的个数对极限强度载荷和浮力系数影响很小。因此，上述的优异参数组合同样也适用于其他多蛋交接耐压壳结构。

4　结论

(1)鹅蛋的蛋形系数符合均值为0.69的正态分布；蛋壳为高度对称性的旋转壳，且与Kitching蛋形函数曲线的相关系数为0.9989，吻合程度最高；作为优选，长轴与偏心距之比取45，蛋形系数取0.69。

(2)多蛋交接耐压壳的临界屈曲载荷远大于极限强度载荷，即极限强度载荷占结构设计的主要因素；多蛋交接耐压壳失稳均发生在交接环肋处，且蛋形壳个数对失稳模式并不影响；蛋形壳个数对极限强度载荷和浮力系数影响很小，可将蛋形壳模型的交接个数简化为3，且不降低计算结果精确度。

(3)多蛋交接耐压壳的主要参数对极限强度载荷和浮力系数综合影响的主次顺序为：加强肋厚度h-蛋形壳长轴长度L-蛋形壳厚度t-加强肋宽度b-加强肋半径a。b、a和h的值对浮力系数影响较小，可以通过调节其值来提高极限强度载荷；t对浮力系数影响较大，其值的增大对提高极限强度载荷的贡献远远小于对有效载荷的损失；L对极限强度载荷和浮力系数影响都较大，可以根据设计适用的水深来确定合适的值，以确保降低浮力系数的同时不降低极限强度载荷。

(4)基于正交试验的三组参数组合h(200mm)-L(3.2m)-t(60mm)-b(90mm)-a(550mm)、h(200mm)-L(2.8m)-t(60mm)-b(75mm)-a(500mm)、h(200mm)-L(2.4m)- t(60mm)-b(90mm)-a(500mm)，可为适用于深海的多蛋交接耐压壳仿生设计提供参考依据，避免参数的盲选和反复试验。

[1]Zhang Jian, Zuo Xinlong, Wang Weibo, et al.Overviews of Investigation on Submersible Pressure Hulls [J]. Advances in Natural Science, 2014, 7(4):54-61.

[2]Ma Ling, Cui Weicheng. Path Following Control of a Deep-sea Manned Submersible Based upon NTSM [J]. China Ocean Engineering, 2005, 19(4): 625-636.

[3]梁学先.潜艇耐压船体特殊问题的研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.

[4]苏玉民,庞永杰.潜艇原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2013.

[5]Pan Binbin, Cui Weicheng. A Comparison of Different Rules for the Spherical Pressure Hull of Deep Manned Submersibles [J]. Journal of Ship Mechanics, 2011, 15(3): 276-285.

[6]苟鹏,崔维成.多球交接耐压壳结构优化问题的研究[J]. 船舶力学, 2009,13(2): 269-277.

Gou Peng, Cui Weicheng. Study of Structural Optimization Problem for Multiple Intersecting Spherical Pressure Hulls [J]. Journal of Ship Mechanics, 2009, 13(2): 269-277.

[7]Liang Chaochung, Shiah Seauwen, Jen Chanyung, et al.Optimum Design of Multiple Intersecting Spheres Deep-submerged Pressure Hull [J]. Ocean Engineering, 2004, 31:177-199.

[8]Ness C C, Simpson W M. A New Submarine Paradigm [J]. Naval Engineers Journal, 2000, 112(4): 143-152.

[9]Blachut J, Smith P. Buckling of Multisegment Underwater Pressure Hull [J]. Ocean Engineering, 2008, 35(2): 247-260.

[10]Blachut J, Jaiswal O R. On Buckling of Toroidal Shells under External Pressure [J]. Comput. Struct.， 2000, 77(3): 233-251.

[11]Zhang Jian, Wang Minglu, Wang Weibo, et al.Biological Characteristics of Eggshell and Its Bionic Application [J]. Advances in Natural Science, 2015, 8(1):41-50.

[12]张建,王明禄,王纬波,等.蛋形耐压壳力学特性研究[J]. 船舶力学,2016，20(1/2)：99-109.

Zhang Jian, Wang Minglu, Wang Weibo, et al. Research on Mechanical Properties of the Eggshell-shaped Pressure Hull [J]. Journal of Ship Mechanics, 2016，20(1/2)：99-109.

[13]Wong H T. Behavior and Modeling of Steel-concrete Composite Shell Roofs [D]. Hong Kong: Hong Kong Polytechnic University, 2005.

[14]Woelke P. Computational Model for Elastic-plastic and Damage Analysis of Plates and Shells [D]. Baton Rouge: Louisiana State University, 2005.

[15]张建.一种深海仿生耐压壳体:中国,10073803.4[P].2015-05-27.

[16]张建,王纬波,高杰,等.深海耐压壳仿生设计与分析[J]. 船舶力学,2015，19(11)：1360-1367.

Zhang Jian, Wang Weibo, Gao Jie, et al. Bionic Design and Analysis of Deepwater Pressure Hull [J]. Journal of Ship Mechanics, 2015，19(11)：1360-1367.

[17]张建.一种仿生耐压装置:中国,10386319.7[P].2015-06-30.

[18]Entwistle K M, Reddy T Y. The Fracture Streng-th under Internal Pressure of the Eggshell of Domestic Fowl [J]. Biological Science, 1996, 263:433-438.

[19]Babich D V. Stability of Shells of Revolution with Multifocal Surfaces [J]. International Applied Mechanics, 1993, 29(11):935-938.

[20]Nedomova S, Severa L. Influence of Hen Egg Shapes on Eggshell Compressive Strength [J]. Int. Agrophysics, 2009, 23:249-256.

[21]王自力,王仁华,俞铭华,等.初始缺陷对不同深度载人潜水器耐压球壳极限承载力的影响[J]. 中国造船, 2007(2): 45-50.

Wang Zili, Wang Renhua, Yu Minghua, et al. Effect of Initial Imperfections on the Ultimate Bearing Capacity of the Pressure Spherical Shell of a Manned Submersible with Different Depth [J]. Shipbuilding of China, 2007(2): 45-50.

(编辑袁兴玲)

Bionic Investigation on Multiple Intersecting Egg-shaped Pressure Hulls

Zhang Jian1,2Zuo Xinlong1Wang Weibo2Tang Wenxian1

1.Jiangsu University of Science and Technology,Zhenjiang，Jiangsu，212000 2.Chinese Ship Scientific Research Center,Wuxi，Jiangsu，214082

Bionic design of multiple intersecting egg-shaped pressure hulls was carried out based on goose egg shell. Firstly, egg-shaped function was established according to a series of biological experiments of egg shells. Then, multiple intersecting egg-shaped pressure hulls in deep sea were designed. Numerical models with 2, 3, 4, 5, 6 eggshells were established. Critical buckling loads, yield loads and buoyancy factors of these hulls were studied. Finally, effects of the main geometric parameters on the performances of the multiple intersecting egg-shaped pressure hulls were analyzed using orthogonal experimental design. The results show that Kitching function is the best egg-shaped function describing goose egg meridian. The length-to-eccentricity ratio is as 45, and the egg shape index is as 0.69. The critical buckling loads of the egg-shaped pressure hulls are larger than yield loads, indicating that strength is the main factor of the structural design. The number of eggshells has little influence on the yield loads and buoyancy factors, while the shell thickness has a great influence on them. The geometrical parameters of the rib have little influence on the buoyancy factors but great on the yield loads.

pressure hull; multiple intersecting egg-shaped; egg-shaped function; bionic design

2015-08-25

国家自然科学基金资助项目(51205173)；江苏省自然科学基金资助项目(BK20150469)；江苏科技大学研究生科研创新计划资助项目(YCX15s-05)

U661.4；TE58

10.3969/j.issn.1004-132X.2016.19.019

张建，男，1984年生。江苏科技大学机械工程学院讲师，中国船舶科学研究中心博士后研究人员。主要研究方向为深海耐压装备现代设计理论与方法。左新龙，男，1991年生。江苏科技大学机械工程学院硕士研究生。王纬波，男，1969年生。中国船舶科学研究中心研究员、博士研究生导师。唐文献，男，1962年生。江苏科技大学机械工程学院教授、博士。