基于改进蚁群算法的机器人末端路径排序优化

张　铁　苏杰汶

华南理工大学，广州，510641



基于改进蚁群算法的机器人末端路径排序优化

张铁苏杰汶

华南理工大学，广州，510641

建立了针对机器人加工时的末端运动路径排序优化问题的数学模型，将该模型转化为广义旅行商问题并用蚁群算法求解。同时对经典的蚁群算法进行了改进，即采用多阶段搜索策略、邻域搜索策略及多蚁种搜索策略，使改进后的蚁群算法能为机器人求取一条更优的末端运动路径。计算机仿真与机器人加工实验结果表明，改进蚁群算法所得的末端运动路径比基本蚁群算法所得结果缩短了3%以上。

机器人；路径排序优化；旅行商问题；改进蚁群算法优化

0　引言

在机器人打磨与雕刻中，为了提高加工效率，需要对机器人末端的运动路径进行优化。路径优化分两种：一是对路径质量的优化，即通过动力学理论与工艺要求来生成质量更优的运动路径，令机器人运动平稳，运动过程中无干涉、无碰撞且令机器人加工的质量更优[1-2]；二是路径排序优化，即采用最优化理论对给定的加工路径进行排序优化，得到最优的加工路径执行顺序，令机器人运动达到时间上的最优[3]。本文研究的路径优化问题属于后者，即：对于工件现有的加工路径，合理地安排它们的执行顺序，令机器人末端在执行加工路径时产生的空行程最短以提高生产效率。空行程是指由于加工路径转换时机器人末端存在抬升、平移、下移等没有产生加工效果的动作。

针对路径的排序优化问题，国内外学者提出了不少方法，大部分都是将此问题转化为旅行商问题(TSP)或广义旅行商问题(GTSP)，然后采用智能算法来求解，如蚁群算法[4-5]、遗传算法[6]等。其中遗传算法鲁棒性强，但其局部搜索能力强而全局搜索能力较弱，易于早熟从而陷于局部最优，而蚁群算法是一种并行进化算法，它模拟蚁群的觅食机制而设计，具有很强的局部收敛能力，但全局收敛性能较差，易于陷入局部最优且收敛的速度较慢[7]，故在使用蚁群算法时须对算法进行改进以获得较好的结果，如最大最小蚂蚁系统算法[8]等。

本文针对机器人末端运动路径优化的问题，建立了一个最优化模型，得出了最优化的目标函数，将这个模型转化为GTSP问题，再用改进的蚁群算法进行了求解。采用邻域搜索策略、多蚁种搜索策略与分阶段搜索策略对蚁群算法进行改进。最后编写程序实现改进的蚁群算法，求解机器人末端运动路径的排序优化问题，并进行实验验证。

1　机器人末端运动路径优化模型

1.1优化模型的建立

如图1a所示，设工件有n条加工路径，加工路径的类型只有直线与多边形两种，当加工路径i为直线时，直线的任一端点均可作该路径的起点si，而另一端点为该路径的终点ei，当加工路径i为多边形时，可以任意选择多边形中的任一顶点作为该路径的起点si，由于多边形为封闭图形，故si、ei为同一点。

图1b中粗实线是工件的加工路径，细实线与虚线为机器人末端的运动路径，“起点”位于s1的正上方。机器人末端在加工时所走的路径如图1a所示。由此可得，在加工工件时，机器人末端的运动路径总长LT为

(1)

而末端运动路径中空行程的长度Linv为

(2)

式中，di为机器人末端下移的高度；ri为机器人末端抬升的高度；ci为机器人末端执行加工路径的长度；mi为末端在空中移动的路径长度。

(a)工件加工路径　(b)机器人末端运动路径图1　加工路径与机器人末端运动路径

为了简化问题，设di=ri=H(i=1,2,…,n)，其中H为常数，此时有

(3)

式中，D(x,y)为x、y两点的距离。

由此可建立机器人末端运动路径的优化模型。设工件有n条加工路径p1,p2,…,pn，合理确定各路径的起点si与ei(i=1,2,…,n)与各加工路径的执行顺序，从而可求

(4)

其中，d(ei,si+1)为点ei与点si+1的欧氏距离，式(4)即为机器人末端运动路径排序优化的目标函数。

1.2将优化模型转化成GTSP问题

上述的路径排序优化模型可以转化为一种特殊的GTSP问题。GTSP可以表述为：有m个城市被分为n个城市群(每个城市群中至少有一个城市，且城市群之间无相同的城市)，求一条最短的回路，即令旅行商从一个城市群中的一个城市出发，遍历每个城市群，且经过每个城市群时至少经过其中的一个城市，最后回到出发点，如图2所示。

图2　广义旅行商问题

在机器人末端运动路径排序优化问题中，每条加工路径就相当于一个城市群，加工路径中的插补点相当于城市群中的一个城市。对于直线类型的加工路径，即相当于只有两个城市的城市群，因为直线类型的加工路径的起点si与终点ei不是同一点，所以旅行商必须经过城市群中的两个城市；对于多边形类型的加工路径，因为其起点si与终点ei均为同一点，所以旅行商只需要经过该城市群中的任意一个城市即可。

由此可将机器人末端运动路径优化问题转化成一个特殊的GTSP问题：设有n个城市群(n为工件加工路径的数目)，每个城市群中至少有两个城市且城市群之间没有相同的城市，求一条最短回路使旅行商从一个城市群中的一个城市出发，有且只有经过每个城市群一次，最后回到起点，当城市群中只有两个城市时，则必须经过该城市群中的这两个城市，否则旅行商只能经过该城市群中的任意一个城市，如图2所示。

设回路的城市依次为：c1,c2,…,ci,…，cl。则回路的长度L定义为

(5)

(6)

L相当于机器人末端运动路径中的总空行程，求式(5)最小值的问题即是求机器人末端运动路径排序优化问题中的最短空行程问题，其与式(4)是等价的。对于式(6)可以解释为：如果ci、ci+1同属一城市群Gj，即相当于两个插补点同属于一加工路径，两点之间的路径并不是空行程，所以它们之间的距离取值为0。

2　蚁群算法及其改进

2.1基本蚁群算法

针对GTSP问题，蚁群算法(ACA)描述为：每只蚂蚁代表一条完整的回路，而评价每只蚂蚁的优劣则根据式(5)、式(6)，L值越小则蚂蚁越优。

(7)

设所有城市的集合为S，其中allowedk={S-tabuk}，表示下一步中允许蚂蚁转移到的城市的集合；α为信息启发因子，表示每条路径上残留信息素的重要程度；β为期望启发因子，表示路径自身启发信息对蚂蚁行进运动的影响力。

当所有蚂蚁对所有城市群进行了一次遍历(即一次循环)之后，需更新所有路径上的信息素，为凸显较优路径的优势，所以采用全局更新规则，即在所有蚂蚁中选出一只路径总长最短的蚂蚁，该蚂蚁对应的路径为当前最优路径，然后仅更新该路径的信息素。τij(t+n)表示t+n时刻路径(i,j)上信息素的量，其更新规则如下[10]：

τij(t+n)=

(8)

(9)

2.2对蚁群算法的改进

基本的蚁群算法拥有很强的全局寻优能力，但它有如下缺陷：①其求解速度较慢，这是由于搜索初期信息素差异不明显，算法的收敛速度较慢，算法的初期浪费了大量的时间所致；②基本蚁群算法中的蚁种单一，所有蚂蚁都是完成同一种任务而无明确的分工，从而导致了算法的求解速度不高，求解能力不强[11]。针对基本蚁群算法的缺点,采用多阶段搜索策略、邻域搜索策略与多蚁种搜索策略对其进行改进。

2.2.1多阶段搜索策略

(10)

(11)

图3　转移概率(t)的放大

2.2.2邻域搜索策略

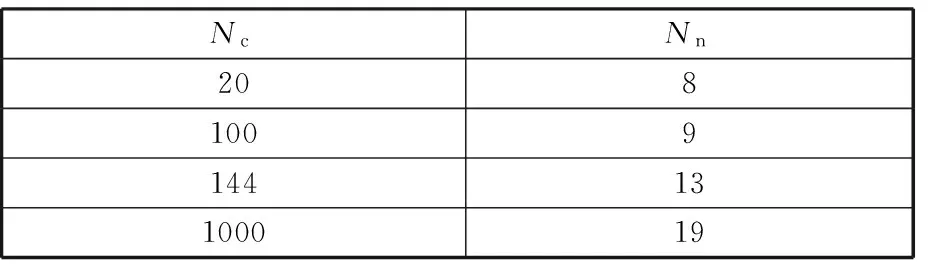
表1　Nc与Nn之间的关系

在得到中心城市i的邻域U(i)后，还要用信息素来标记城市i到其邻域的路径，其标记规则如下[11]：

(12)

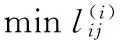
然后将标记的信息素加到各路径中去，从而得到初始时刻各路径的信息素为[11]

(13)

2.2.3多蚁种搜索策略

(14)

(15)

传统蚁有很强的局部搜索能力，而叛逆蚁与反叛蚁则是真正意义上的全局搜索，可以提高算法所得解的全局最优性。

改进的蚁群算法步骤如下：

(1) 初始化参数，包括蚂蚁数目m、传统蚁的比例p、城市群数Ng、循环总次数为N、前期阶段循环次数为N′、初始时刻各路径信息素含量τo、信息启发因子α、期望启发因子β、信息素强度Q、挥发系数ρ。

(2) 计算各城市的邻域，并按式(12)、式(13)初始化各路径上的信息素。

(3) 初始化蚁群，每只蚂蚁k随机选择一个城市群，然后在该城市群中随机选择一个城市作为出发点，将该城市加入到蚂蚁路径pathk中，而将蚂蚁所在城市群中的所有城市加入到禁忌表tabuk中。

(4) 循环次数n←0。

(5) 设时刻t←0，则

Fort=0,1,2,…,Ng-2Then

Fork=1,2,…,mThen

k←k+1

End

t←t+1

End

(6) 根据式(5)、式(6)计算所有蚂蚁的路径中空行程的总长度，选出L值最小的蚂蚁，并根据式(2)、 式(3)更新各路径上的信息素。

(7) n←n+1。

(8) 如果n=N则终止算法，输出最优结果，否则返回步骤(5)。

3　仿真与实验结果

为了验证改进蚁群算法的有效性，分别采用基本蚁群算法与改进蚁群算法对三个不同工件的加工路径进行优化，比较优化的机器人末端运动路径中的空行程长度。由于本文研究的是运动路径排序优化问题，工件的加工路径是给定的，优化的是加工路径的执行顺序，为了简化问题，故实验中工件的所有路径都位于同一平面上。三个工件的加工路径数目分别为47、104与192,如图4所示。

(a)工件一(47条轨迹)

(b)工件二(104条轨迹)

(c)工件三(192条轨迹)图4　实验的工件轨迹

改进蚁群算法与基本蚁群算法的参数设置为：蚂蚁数目m与加工路径的数目相同，城市群数Ng与加工路径数目相同，循环总次数为N=100，初始时刻各路径信息素含量τo=1，信息启发因子α=1.0，期望启发因子β=10.0，信息素强度Q=100，挥发系数ρ=0.1；而对于改进蚁群算法而言，前期阶段循环次数为N′=35，传统蚁比例为0.77。在计算机上进行仿真计算，所得结果如表2所示。

表2　工件的刀具路径优化的仿真结果比较

从表2、表3的数据可得：①对机器人末端运动路径进行优化后，其中的空行程长度会减少62.8%～86.4%；②改进蚁群算法的优化结果与基本蚁群算法优化结果相比，空行程减少1.13%～3.86%，而且随着问题规模的增大，其优势会更加明显；③改进蚁群算法与基本蚁群算法相比，改进蚁群算法的全局搜索能力更佳，更快地跳出局部最优，从而避免浪费大量的循环迭代时间。

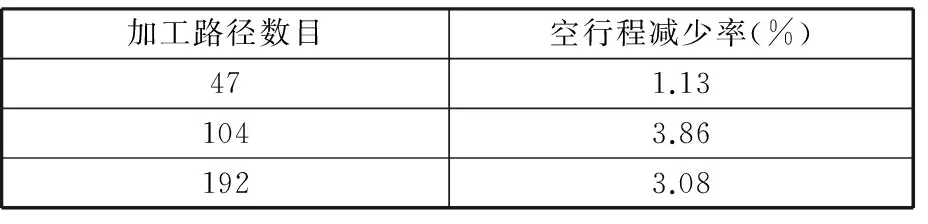
表3　改进蚁群算法与基本蚁群算法改进效果比较

在实验平台上进行平面雕刻实验，对表2中的三种工件进行加工，分别采用未优化前、基本蚁群算法优化后、改进蚁群算法优化后的机器人末端运动路径进行加工，同时测量整个加工的时长，由时长来验证优化后空行程是否真的减少。改进蚁群算法与基本蚁群算法的改进效果比较如表3所示。

实验条件： 采用直角坐标机器人平台，如图5a所示，运动方式采用OXYZ三坐标直线插补，合成插补速度为4 mm/s，合成加速度为50 mm/s2，插补段终点速度为0，在一个平面上进行雕刻加工，雕刻的深度为0.5 mm，机器人末端的抬升高度r与下降高度d均为3 mm，所用刀具为φ3的端面铣刀。加工过程如图5b所示。

(a)直角坐标机器人平台　　　(b)加工过程图5　实验过程

由表4可知，对于同一工件，对机器人末端运动路径进行蚁群算法优化后，其加工时长大幅缩短，而进行了改进蚁群算法优化后，其加工时长最短。由表5可知，随着加工路径数目的增大，改进蚁群算法的优化效果相对于基本蚁群算法的优化效果而言，会节省更多的时间。结果与仿真结果一致。雕刻的工件如图6所示。

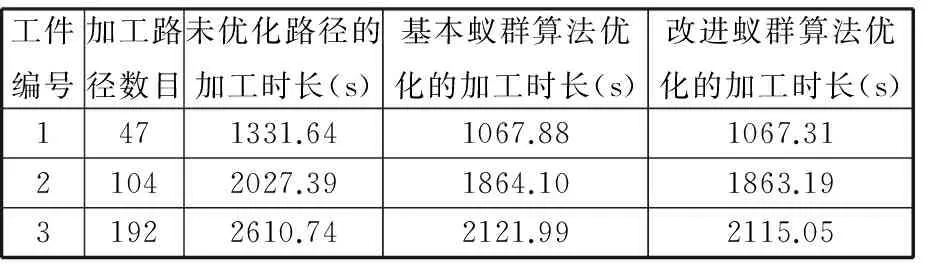
表4　优化前后末端运动路径的加工时长比较

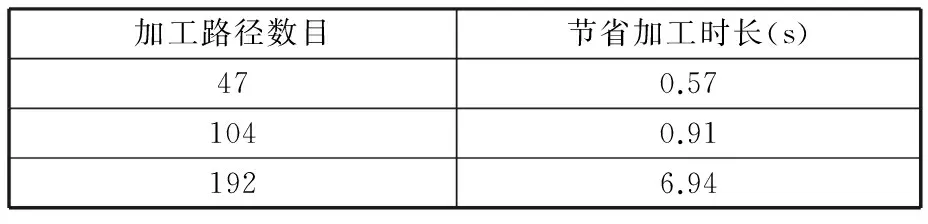
表5　改进蚁群算法与基本蚁群算法优化的实验效果对比

(a)工件加工路径　　　　(b)加工工件效果图6　工件加工效果

4　结论

本文采用蚁群算法对机器人加工时的末端运动路径进行了排序优化，并对传统的蚁群算法提出了改进措施，即采用了多蚁种、多阶段搜索、邻域搜索三种策略，使改进后的蚁群算法的优化结果更优。仿真实验结果表明，采用改进蚁群算法优化后的机器人末端运动路径中的空行程比基本蚁群算法的优化结果短3%；而在实际的机器人雕刻实验中，采用改进蚁群算法优化后，对同工件的加工时间最短，在实验中最大节省时间为6.94 s，从而证明了改进蚁群算法的有效性。

本文主要研究减少雕刻加工中不同区域空行程问题，因此实验仅仅进行了平面的雕刻实验，本文的成果可以推广到机器人曲面雕刻与打磨加工。

[1]王伟,贠超,张令. 机器人砂带磨削的曲面路径优化算法[J]. 机械工程学报,2011,47(7):8-15.

Wang Wei, Yun Chao, Zhang Ling. Optimization Algorithm for Robotic Belt Surface Grinding Process[J]. Journal of Mechanical Engineering, 2011,47(7):8-15.

[2]晁永生,刘海江. 白车身焊接机器人加工路径优化和仿真[J]. 中国机械工程,2010,21(4):442-445.Chao Yongsheng, Liu Haijiang. Welding Robot Path Optimization and Simulation for Body in White[J]. China Mechanical Engineering， 2010,21(4):442-445.

[3]Alatartsev S, Stellmacher S, Ortmeier F. Robotic Task Sequencing Problem: a Survey[J]. Intell. Robot Syst., 2015, 80:279-298

[4]Li Cuiming, Gong Jun, Niu Wancai ，et al. Combinatorial Optimization of Spray Painting Robot Tool Trajectory Based on Improved Membership Cloud Models Ant Colony Algorithm[J]. Journal of Shanghai Jiaotong University, 2015，49(3)：387-391.

[5]Wang Mei, Meng Shengda. Path Planning Method of Water-jet Cutting Robot[J]. Journal of Southeast University (Natural Science Edition),2012，42(S):212-216.

[6]Baizid K, Chellali R, Yousnadj A, et al. Genetic Algorithms Based Method for Time Optimization in Robotized Site[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Taipei, 2010:1359-1364.

[7]Saenphon T, Phimoltares S, Lursinsap C. Combi-ning New Fast Opposite Gradient Search with Ant Colony Optimization for Solving Travelling Salesman Problem [J]. Engineering Applications of Artificial Intelligence，2014，35：324-334.

[8]李士勇, 陈永强, 李研. 蚁群算法及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社，2004.

[9]Yang Jinhui, Shi Xiaohu. An Ant Colony Optimization Method for Generalized TSP Problem [J]. Progress in Natural Science,2008,18:1417-1422.

[10]Liu Dan, Zheng Lijuan, Wang Jianmin. Applica-tion of Improved Ant Colony Algorithm in Solving TSP[J]. International Journal of Multimedia and Ubiquitous Engineering,2014,9(7):395-402.

[11]王霜. 大型TSP问题的蚁群优化规则研究[D].长春：吉林大学,2012.

[12]Kan Junman, Zhang Yi. Application of an Improved Ant Colony Optimization on Generalized Traveling Salesman Problem[J]. Energy Procedia,2012,17:319-325.

[13]全惠云，文高进. 求解 TSP 的子空间遗传算法[J]. 数学的理论与应用，2002，22(1):36-39.

Quan Huiyun, Wen Gaojin. Subspace Genetci Algorithm for TSP[J]. Mathematical Theory and Applications，2002, 22(1):36-39.

(编辑袁兴玲)

Path Sorting Optimization of Robotic End-effector by Improved ACA

Zhang Tie Su Jiewen

South China University of Technology，Guangzhou，510641

For the path sorting optimization of robotic end-effector in robotic machining , a solution was presented, that established mathematical model for this problem and converted it to generalized traveling salesman problem (GTSP) and solved this problem by ACA. Meanwhile, the classical ACA was improved with multi stage search strategy, neighborhood search strategy and multi ant type strategy, so that the improved ACA was able to calculate a more optimized end-effector path for robotic machining. The results of simulation and robotic machining prove that the end-effector path obtained by improved ACA is shorter than 3% above the basic ACA’s.

robot; path sorting optimization; traveling salesman problem (TSP); improved ant colony algorithm (ACA) optimization.

2015-12-07

国家科技重大专项(20152X04005006);广东省科技计划重大专项(2014B090921004，2014B090920001)

TP242.2

10.3969/j.issn.1004-132X.2016.19.011

张铁，男，1968年生。华南理工大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为工业机器人、服务机器人及自动化设备等。 发表论文100余篇。苏杰汶，男，1991年生。华南理工大学机械与汽车工程学院硕士研究生。