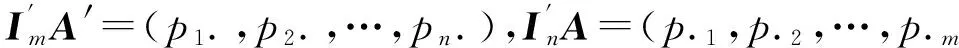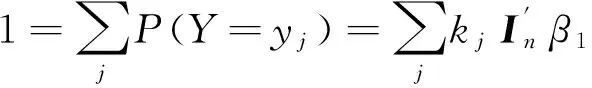二维离散型随机变量相互独立的判别准则*

陶　宝

(重庆工商大学 数学与统计学院,重庆 400067)



二维离散型随机变量相互独立的判别准则*

陶宝

(重庆工商大学 数学与统计学院,重庆 400067)

在二维随机变量独立性定义的基础上，根据联合概率分布与边缘概率分布的关系，给出了二维离散型随机变量独立性的判定定理；通过引入联合概率分布矩阵概念，从矩阵形式、矩阵的秩以及向量线性关系的角度，提出了判别独立性的新方法.

二维离散型随机变量；相互独立；联合概率分布矩阵；秩

设二维随机变量(X，Y)的联合概率分布函数为F(x，y)，随机变量X和Y的边缘概率分布函数分别为FX(x)，FY(y)，若对任意x，y∈R，都有

(1)

则称随机变量X与Y相互独立.

若(X，Y)为二维离散型随机变量，联合概率分布列为

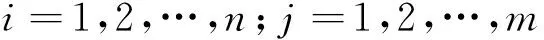
文献[1]和[2]指出，随机变量X和Y的边缘分布列分别为

联合概率分布列和边缘概率分布列可以反映在同一个表格中，见表1.

表1　联合概率分布列与边缘概率分布列

若(X，Y)是二维连续型随机变量，文献[3]讨论了(X，Y)变换的概率分布，文献[4-5]讨论了X与Y相互独立性的判定准则.若(X，Y)为二维离散型随机变量，关于X与Y相互独立性的判定，文章给出了若干结论.

定理1对于二维离散型随机变量(X，Y)，X与Y相互独的充分必要条件是：

(2)

证明只需证明式(1)和式(2)等价.假设式(1)成立，为证式(2)，不妨假设x1

即式(2)成立．反过来，假设式(2)成立，那么

即式(1)成立，于是式(1)和式(2)等价.

在实际问题中，经常碰到二维离散型随机变量(X，Y)的取值为有限对的情形，这时它的联合概率分布列和边缘概率分布列可用矩阵形式表示.矩阵

由矩阵乘法的定义和定理1，立即可得以下结论.

定理2对于二维离散型随机变量(X，Y)，X与Y相互独立的充分必要条件是：

(3)

由矩阵的秩的性质，对矩阵A和B，有秩(AB)≤min{秩(A)，秩(B)}，结合定理2，立即得到以下结论.

定理3对于二维离散型随机变量(X，Y)，X与Y相互独立的充分必要条件是A的秩为1.等价地，X与Y不相互独立的充分必要条件是A的秩大于1.

证明若X与Y相互独立，由定理2知，秩(A)≥1，秩(AIm)=1，于是秩(A)=1.

反过来，若A的秩为1，记A=(β1，β2，…，βm)，不妨设A的列向量组β1，β2，…，βm的极大无关组为β1，则β1，β2，…，βm均可由β1线性表示，记为βj=kjβ1(j=1，2，…，m).于是有：

即X与Y相互独立.

由定理3，立即可得以下推论：

推论1对于二维离散型随机变量(X，Y)，X与Y相互独立的充分必要条件是矩阵A中任意两个行(列)向量线性相关；等价地，X与Y不相互独立的充分必要条件是在矩阵A中存在两个行(列)向量线性无关.

推论2对于二维离散型随机变量(X，Y)，X与Y相互独立的充分必要条件是矩阵A中任意两行(列)元素对应成比例；等价地，X与Y不相互独立的充分必要条件是在矩阵A中存在两行(列)元素对应不成比例.

[1] 袁德美,安军,陶宝.概率论与数理统计[M].北京:高等教育出版社,2011

YUAN D M,AN J,TAO B.Probability Theory and Mat-hematical Statistics[M].Beijing:Higher Education Press,2011

[2] 茆诗松,程依明,濮晓龙.概率论与与数理统计教程[M].北京:高等教育出版社,2011

MAO SH S,CHENG Y M,PU X L.Probability Theory and Mathematical Statistics Tutorial[M].Beijing:Higher Edu-cation Press,2011

[3] 陶宝,袁德美.二维连续型随机变量变换的概率分布[J].重庆工商大学学报(自然科学版),2015,32(5):34-36

TAO B,YUAN D M.Probability Distribution of the Mapping for the Bivariate Continuous Random Variable[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2015,32(5):34-36

[4] 王群,彭小帆.二维连续型随机变量相互独立的一个充分条件[J].大学数学,2015,31(5):72-75

WANG Q,PENG X F.A Sufficient Condition for the Independence of Two-dimensional Continuous Random Varia-bles[J].College Mathematics,2015,31(5):72-75

[5] 刘春霞.二维连续型随机变量独立性的判定[J].长春大学学报,2015,25(4):53-55

LIU CH X.Determination of Independence of Two-dimen-sional Continuous Random Variables[J].Journal of Chang-chun University,2015,25(4):53-55

责任编辑：李翠薇

Criterion for the Mutual Independence of Bivariate Discrete Random Variables

TAO Bao

(College of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)

Based on the independence definition of bivariate random variables, according to the relationship between the joint probability distribution and marginal probability distribution, the critical theorem is introduced for the independence of bivariate discrete random variables. With the concept of the joint probability distribution matrix, the new methods of judging independence are given from the aspect of matrix representation, the rank of matrix and linear relations among vectors.

bivariate discrete random variables; mutual independence; joint probability distribution matrix; rank

10.16055/j.issn.1672-058X.2016.0005.019

2016-01-07;

2016-03-02.

重庆工商大学教育教学改革研究重点项目(130114)；重庆市教委教学改革项目(1203057).

陶宝(1979-)，男，四川达县人，讲师，硕士，从事极值理论研究.

G642

A

1672-058X(2016)05-0095-03