叶素动量理论(BEM)实现方法讨论
叶素动量理论(BEM)实现方法讨论

叶素动量理论(BEM)是翼式流体机械叶片设计中广泛采用的方法,它通过求解一组代数方程,获得叶片结构及性能参数。对水平轴风力机来说,空气流过叶轮时一方面沿主流方向流动,另一方面作与叶轮旋转方向相反的圆周运动,同时由于叶片附近剪切流的作用,在叶片后方形成叠加于螺旋形流线上的涡旋运动。考虑到空气流动沿主流方向和切线方向的动量损失,引入轴向诱导因子和切向诱导因子来计算叶间和叶片尾部气流轴向和切向速度。关于应用叶素动量理论进行风力机叶片设计的计算步骤在许多文献中均有所论述。叶片设计计算需要确定的参数包括叶片弦长、叶片流动角、叶片攻角、叶片扭转角以及轴向和切向诱导因子等参数,它们在设计之初都是未知的,且相互影响。与一般工程设计类似,在开始设计时需要先假定一些几何或结构参数,通过迭代或优化的过程获得满足设计性能要求的几何参数。在现有文献中,关于如何确定叶片有关几何参数的初始分布介绍较少,本文在分析叶素动量理论实施步骤的基础上上介绍几种确定轴向诱导因子和切向诱导因子的方法以及确定叶片弦长的方法,进一步明确叶素动量理论的实现过程。
叶素动量理论的基本模型
叶素动量理论建立在叶素气动理论和动量守恒原理的基础上。叶素速度三角形和力矢量图如图1所示。
图1中,D为阻力;L为升力;Fn为轴向力;Ft为切向力;V∞(1-a)为轴向速度;Ωr(1+b)为切向速度;V∞为风轮上游远方风速;Ω为风轮旋转角速度;W 为风轮处气流相对速度;a 为轴向诱导因子;b 为切向诱导因子;α为攻角;β为扭转角;φ为流动角。根据文献,轴向诱导因子a 、切向诱导因子
b 分别由式(1)和式(2)定义。

式中,V 为叶间气流轴向速度分量;ω为叶间气流角速度,其方向与叶轮(或风轮)转动方向相反。
根据动量守恒和动量矩守恒原理,气流作用于叶素的推力(轴向力)和力矩可通过式(3)和式(4)表示。

叶素单元效率ηr、当地风能利用系数dCP可表示为:

轴向诱导因子和切向诱导因子的关系式为:


图1 典型叶素速度三角形和力矢量图

式(8)和式(9)中,B为叶片个数;c为叶片弦长。分别联立式(3)与式(8)及(4)与式(9),得到轴向诱导因子和切向诱导因子与叶片弦长、翼型气动参数及流动角的关系式:

或

由式(10)和式(11)可进一步将轴向诱导因子和切向诱导因子写成显式的形式。若不计空气阻力,则轴向诱导因子和切向诱导因子的关系式又可表示为:

式(3)—式(14)即为叶素动量理论的基本关系式。
叶素动量理论的实现方法
从式(10)—式(13)可知,叶素几何参数、气动参数及诱导因子互为函数关系,给方程的求解带来一定困难,但是分析式(10)—式(13)并结合叶素速度三角形可一发现,翼型气动参数是叶片设计的基础数据,诱导因子是设计过程的中间参数,因此叶片设计可首先从翼型气动参数入手。
攻角α的确定
叶素动量理论假定沿叶片径向叶素气动特性是独立的,其气动特性用翼型的气动特性表示。翼型的气动特性根据翼型实验或计算获得。升力系数CL和阻力系数CD分别是攻角α和雷诺数Re的函数,即:

雷诺数Re根据相对速度W 和弦长c 定义:

其中,ν为空气运动粘度。
轴向诱导因子和切向诱导因子的确定
在简化计算中,轴向诱导因子a 和切向诱导因子b可根据式(5)和式(7)或式(6)和式(14)来确定。
将式(5)和式(7)分别对切向诱导因子b求一阶导数,并令其为零,可得:
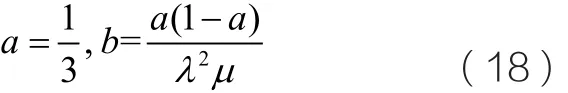
以式(6)最大为目标函数,以式(14)为约束条件,通过求解这一约束优化优化问题便可得到轴向诱导因子a 和切向诱导因子b ,即:

以上两种确定轴向诱导因子和切向诱导因子的方法都有一定的局限性,前者仅考虑了动量变化的因素,未考虑叶片气动效应;后者优化模型的约束条件根据假设气动阻力为零得出,因而两者均不能保证同时满足气动力平衡及动量守恒的要求。
叶片初始几何参数的确定
由图1可知,流动角φ与攻角α和扭转角β的关系为:

由速度三角形可得:

若已知轴向诱导因子和切向诱导因子,由式(22)可得流动角φ,根据最佳攻角αopt由式(21)便可得到扭转角β。但最佳攻角αopt是Re的函数,Re又与弦长c有关。由此可知,如何确定弦长或弦长的分布成为需要解决的另一关键问题。若把获得叶轮最大风能利用系数作为目标函数,弦长c、叶尖速比λtip的变化范围作为约束条件,建立优化模型,即:

通过求解这一优化问题,便可获得叶片的几何参数及运行参数。但由于优化过程中,设计变量的取值是任意的,不能保证沿叶片展向弦长和扭转角的连续性。
关于叶片弦长和扭转角沿叶片展向的变化,文献以不同的计算模型进行了介绍,文献 将这些方法归纳为简化圆盘理论设计模型(Betz模型)、Schmitz 设计模型、Glauert 设计模型以及Wilson 设计模型,并给出前三种模型的计算公式,文献将基于式(19)、(20)的计算方法称为Wilson设计模型。除Betz模型外,其他三种模型均考虑了涡流的影响,但认为翼型阻力对叶片结构影响较小,在计算弦长和扭转角时略去了翼型阻力的影响。如文献推导了不计翼型空气阻力并假定轴向诱导因子和切向诱导因子按式(18)计算的情况下,流动角和叶片组合结构参数的分布的计算公式,由此可预测叶片弦长的分布。以最大风能利用系数为目标设计出的叶片,根部弦长往往很大,不易加工且增加叶片重量,因此需作修正,文献 以采用NACA4412翼型设计出的叶片为例,认为可在叶片展向70%和90%处连线延伸叶片获得统一锥度的叶片设计。文献给出用线性和样条函数修正叶片弦长的方法。文献也指出,理想叶片的弦长和扭角沿展向呈非线性变化,叶根处的弦长及扭角均较大,需要对弦长和扭角进行修正。应用Schmitz 设计模型、Glauert 设计模型以及Wilson 设计模型计算叶片弦长时仍然要用到升力系数,在叶片弦长未知时,升力系数将无法确定,只能根据假设的雷诺数和攻角来确定,或采用理想流体绕流翼型时的升力系数。
从实用的角度出发,文献 给出按指数规律分布的弦长计算式:

给定叶片叶根和叶尖的弦长后,根据式(25)可确定系数b1和指数b2。以Wilson 设计模型为基础,考虑弦长修正,确定叶片根部和尖部弦长后根据式(25)可获得具有较好性能的弦长分布。

图2 叶片弦长分布

图3 叶片扭转角分布

图4 叶素单元效率
计算实例
考虑一小型风力机,风力机功率为10kW,传动装置效率η=0.8,叶片数B=3,设计风速V∞=8m/s,初选风能利用系数CP=0.4。风轮直径,风力机转速按式(25)、(26)计算。叶尖:

速比λtip=7,确定叶根弦长、叶尖弦长分别为croot=0.65m、ctip=0.25m。叶片断面翼型选为SG6043翼型。主要计算步骤如下:
1)应用式(25)计算叶片弦长分布;
2)采用XFOIL软件或其它软件计算不同雷诺数、不同攻角下翼型升力系数和阻力系数,找出每一雷诺数下最大升阻比对应的攻角,即αopt=fα(Re,εmax);
3)应用迭代计算法,初设轴向诱导因子aold=1/3、切向诱导因子bold=0.1;
4)根据式(22)、(21)计算流动角和扭转角;
5)根据式(10)、(11)得出更新的轴向诱导因子anew、切向诱导因子bnew;
6)计算轴向诱导因子和切向诱导因子差值:∆a,∆b,并判断差值的绝对值是否小于给定的误差限,若满足则执行下一步,否则更新轴向诱导因子和切向诱导因子,转第4)步;
7)根据式(5)、(6)计算叶素单元效率ηr、当地风能利用系数dCP,对dCP积分获得风力机叶轮的风能利用系数CP。根据需要也可计算其他性能参数。
计算中,叶尖损失修正因子按文献给出的公式计算。叶片弦长、扭转角、叶素单元效率计算结果如图2-图4所示。
图2所示叶片根部位于半径比r/ R =0.05处,叶片根部与轮毂连接采用圆柱形过渡。由图4可以看出,叶素单元效率最大值位于半径比r/ R =0.8附近,最大值为0.54。叶轮风能利用系数为0.48,按此方法可使风轮获得较高的性能。
结束语
叶素动量理论是风力机叶片设计实用的工程方法。空气绕流叶片的运动是具有涡旋的复杂流动,通过引入轴向诱导因子和切向诱导因子反映气流沿轴向和切向速度的变化,使基于动量守恒原理和气动理论的分析方法成为可能。根据对涡流及诱导因子计算方法的不同形成不同的计算模型,在应用叶素动量理论设计叶片时,各种参数互相影响,但确定叶片各断面合理的弦长是设计过程的重要环节,考虑到对理性情况下弦长的修正,采用多项式或指数规律变化的弦长分布可简化计算过程并能获得较高的风能利用系数。
10.3969/j.issn.1001- 8972.2016.18.029

