功率分流式齿轮系统均载特性影响因素分析

姚　澜，赵　兵，徐景文，刘　潇，周国涛

（1.西北工业大学，西安 710072；2.北京宇航系统工程研究所，北京 100076）

功率分流式齿轮系统均载特性影响因素分析

姚澜1，赵兵2，徐景文2，刘潇2，周国涛2

（1.西北工业大学，西安 710072；2.北京宇航系统工程研究所，北京 100076）

为了提出功率分流式齿轮系统有效的均载方法，对其进行了均载特性影响因素分析。采用动力学分析方法，建立了功率分流式齿轮系统动力学模型，通过对齿轮副特征矩阵进行装配快速的形成了系统动力学方程，并对动力学模型中激励参数的计算进行了分析。通过定义均载系数衡量均载性能，啮合误差、耦合刚度、支撑刚度和转速被认为是影响均载的主要因素，分析了其对均载系数的影响规律。研究得出：减小啮合误差和耦合刚度、增大支撑刚度，以及选取合适的工作转速有利于提高功率分流式齿轮系统的均载性能。提出的有效均载方法包括：提高加工精度，设计合理结构使系统具有软耦合、硬支撑，选取合适工作转速。

功率分流；均载特性；动力学；均载影响因素；均载方法

0　引言

功率分流式齿轮系统因其具有大功重比、高安全性和可靠性、大减速比和低振动噪声等优点，在航空传动中已替代行星传动，应用于先进的直升机主减速器中。虽然功率分流式齿轮系统具有众多优点，但是Kish［1］研究发现其载荷分配不均的问题更加突出。

针对多支路齿轮系统的均载问题，相关学者进行了大量研究，主要采用动力学分析方法，通过定义基于齿轮啮合力的均载系数衡量均载性能。Krantz［2］研究发现，功率分流式齿轮系统虽然布局形式对称但是其受力形式非对称，不均载是系统的固有特性，同时分析了不同摩擦状态下系统的均载特性。Kahraman［3］和Guo［4］等研究了不同误差大小和不同工况条件时行星传动系统均载特性的变化规律。Ligata和Kahraman等［5］分析了不同类型加工误差变化时行星传动系统均载系数的变化规律。付晨曦［6］等研究得出系统参数对分扭传动的均载性能影响较大。

Kahraman［3］指出，针对多支路齿轮系统均载问题的研究，旨在对均载建立全面的认识，从而进一步提出有效的均载方法。本文在前人研究的基础上，针对一些影响均载的关键因素，进行均载特性影响因素分析，在此基础上提出有效的均载方法。

以功率分流式齿轮系统为研究对象，采用动力学分析方法，建立了系统动力学模型，通过定义均载系数衡量系统均载性能。分析了啮合误差、扭转刚度、支撑刚度和转速对功率分流式齿轮系统均载特性的影响规律。根据分析结果提出了提高功率分流式齿轮系统均载性能的有效方法。

1　系统动力学模型

某功率分流式齿轮系统［2］如图1所示，该系统属于两支路功率分流式齿轮系统。传动系统分为两级传动，第一级采用斜齿轮，第二级采用直齿轮，传动系统中大斜齿轮和小直齿轮安装在一根双联齿轮轴上。

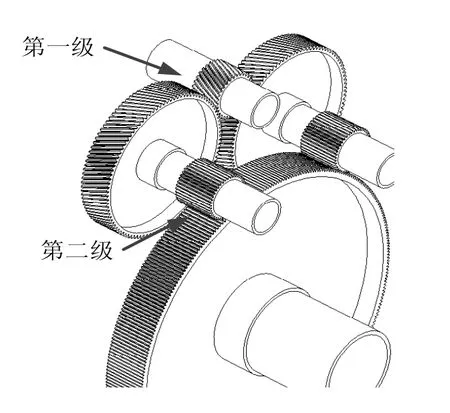
图1　某功率分流式齿轮系统示意图

图2为功率分流式齿轮系统坐标系示意图。系统中小斜齿轮、左侧大斜齿轮、右侧大斜齿轮、左侧小直齿轮、右侧小直齿轮和大直齿轮依次标记为齿轮1～6，系统两支路分别标记左、右（L、R）。

如图2所示，传动系统中x轴方向由O2指向O3，y轴方向由O1指向O4，x×y为z轴方向，由此建立了传动系统广义坐标系。传动系统广义位移如式（1）所示，每个齿轮具有沿x、y、z轴方向的平动广义位移和绕z轴方向的转动广义位移。

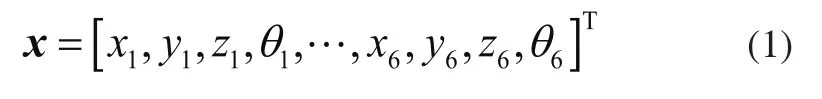
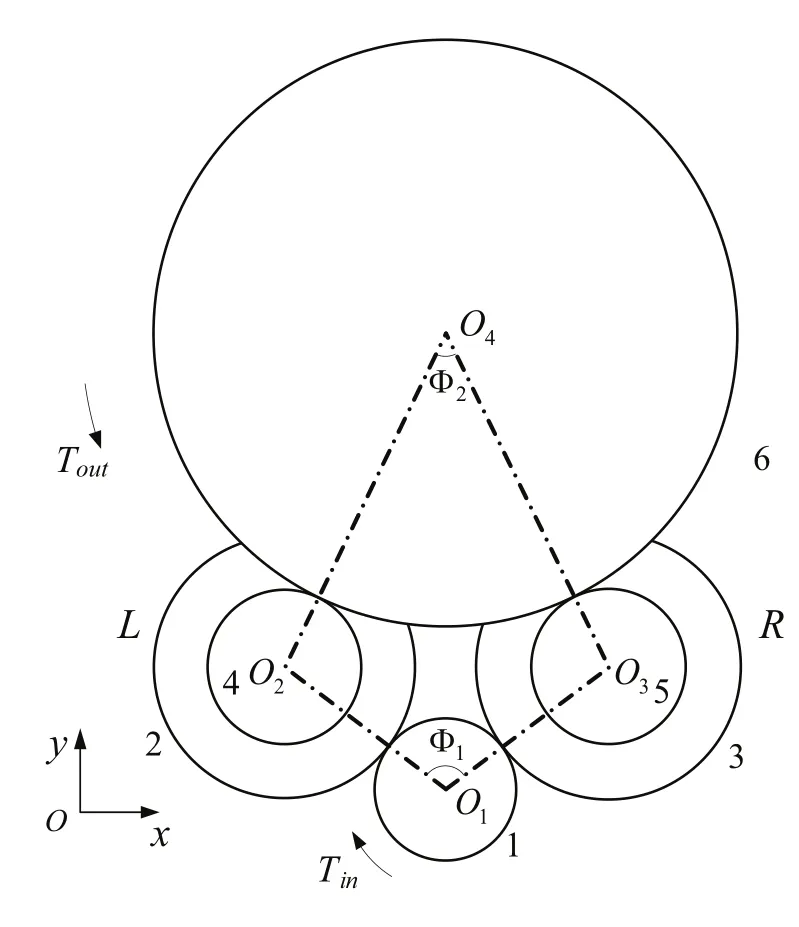
图2　功率分流式齿轮系统坐标系示意图

建立的系统动力学方程，如式（2）所示。

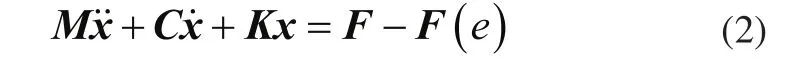
式中：M为质量矩阵，如式（3）所示；C为阻尼矩阵，采用瑞利阻尼进行模拟，如式（4）所示；总刚度矩阵K=Km+Kc+Kxy，为齿轮啮合刚度矩阵Km、齿轮间的耦合刚度矩阵Kc、齿轮支撑刚度矩阵Kxy之和，啮合刚度矩阵Km和耦合刚度矩阵Kc见式（5），支撑刚度矩阵Kxy见式（10）；F为外载荷矩阵，见式（11）；F（e）为由误差引起的弹性力矩阵，见式（12）。

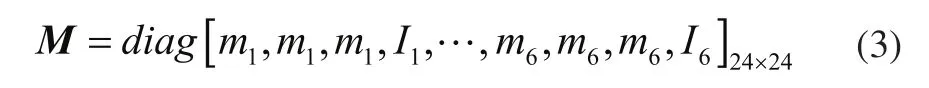
式中：m和I分别为齿轮的质量和转动惯量。

式中：α、β为瑞利阻尼系数。

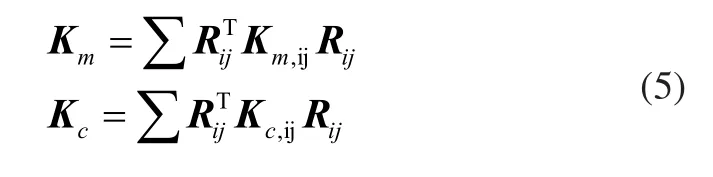
式中：Km，ij为齿轮i和齿轮j啮合时形成的啮合刚度矩阵，见式（6）；Kc，ij为齿轮i和齿轮j间形成的耦合刚度矩阵，见式（7）；Rij为2×6的分块稀疏矩阵，各子矩阵维数相同，见式（8）。

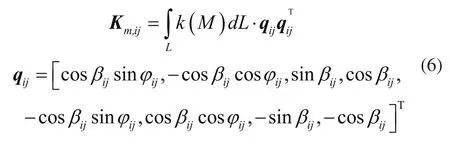
式中：k（M）为啮合平面内接触线上任意接触点M处的啮合刚度，ijφ为从y轴正向到啮合线正向（从动轮指向主动轮）逆时针的夹角，ijβ为基圆螺旋角。

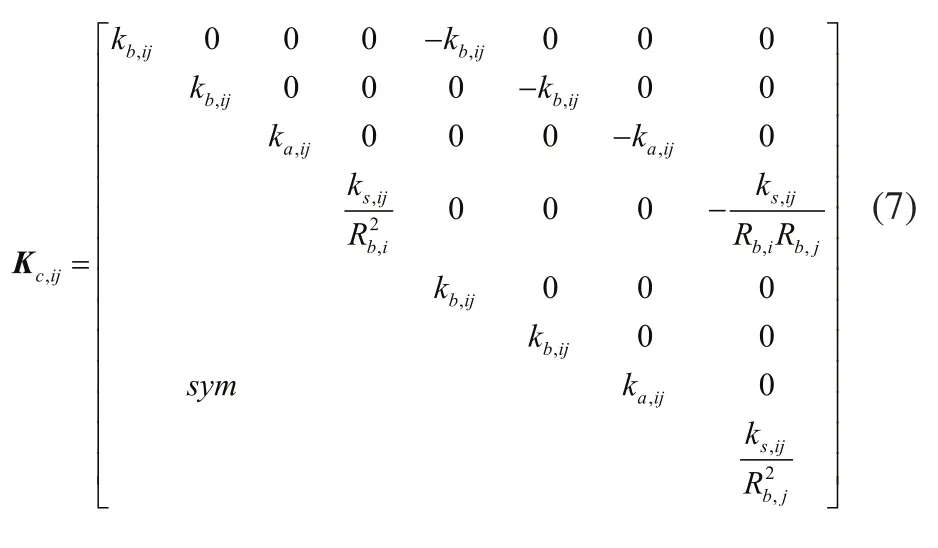
式中：ks，ij、kb，ij、ka，ij分别为齿轮i和齿轮j之间形成的扭转、弯曲和拉压刚度，Rb，i、Rb，j为齿轮i、齿轮j的基圆半径。

式中：子矩阵R1i和R2i的表达式为：

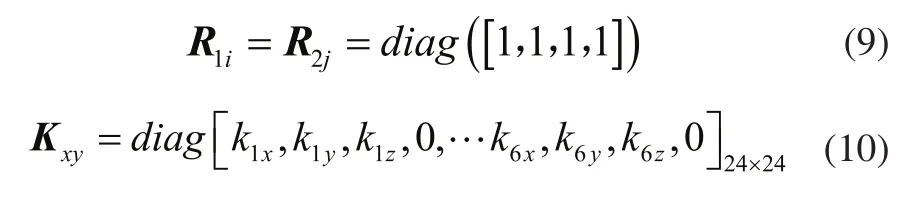
式中：kx、ky为齿轮径向支撑刚度，kz为齿轮轴向撑刚度。

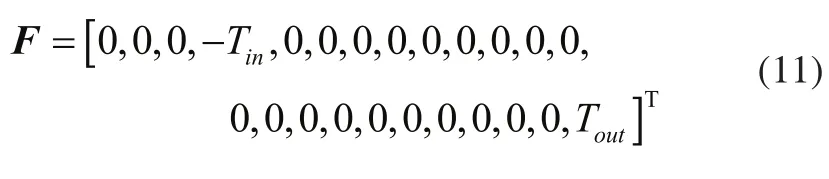
式中：Tin和Tout分别为系统输入、输出扭矩。

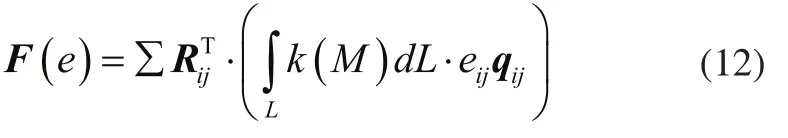
式中：e为齿轮i和齿轮j啮合时形成的啮合误差。

2　激励参数分析

本文在计算齿轮副啮合刚度时假设啮合平面内接触线上任意接触点处的啮合刚度为定值，任意时刻的接触线长度时变［7］，由此任意时刻的齿轮副啮合刚度可按照式（13）进行计算。

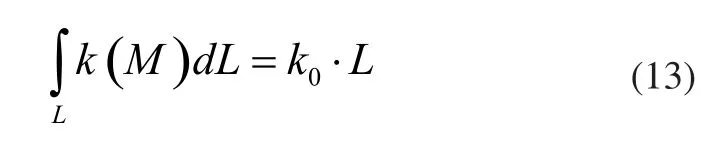
式中：k0为任意接触点处的啮合刚度，可根据ISO6336进行计算；L为接触线长度，可根据接触状态判断得出。

加工误差形成齿轮副啮合误差，啮合误差在动力学模型中通常通过一种周期性的位移激励进行模拟，此处采用正弦函。

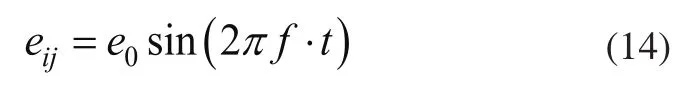
式中：e0为啮合误差幅值，f为啮合频率。

3　均载系数定义

定义系统均载系数如式（15）所示，均载系数越小表明系统的均载性能越好。

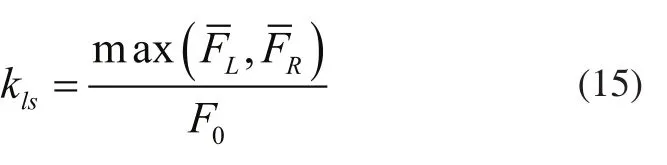
式中：FL、FR分别为小斜齿轮两支路动态啮合力的平均值，F0为小斜齿轮单侧支路的静态啮合力。

小斜齿轮动态啮合力和静态啮合力的计算公式如式（16）、式（17）所示。

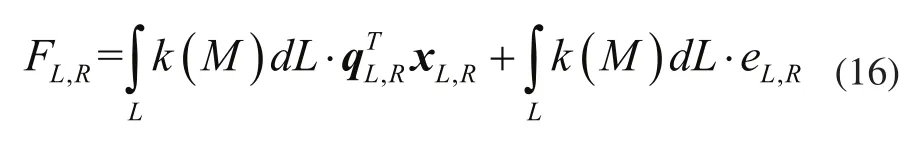
式中：qL，R、xL，R、eL，R分别为左、右两侧斜齿轮副的方向矢量、广义位移和啮合误差。

式中：Rb1为小斜齿轮基圆半径。

4　均载影响因素分析

某功率分流式齿轮系统参数［2］如表1所示。系统的标准输入功率372.85kW、转速8780r/min，材料9310钢，安装角Ф1、Ф2分别为48.4°、116.28°。

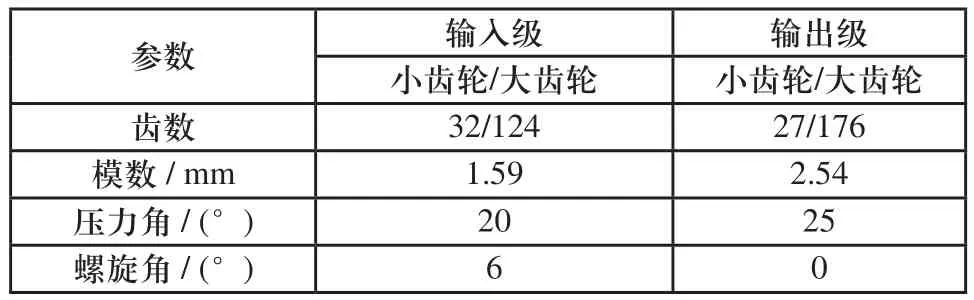
表1　某功率分流式齿轮系统参数［2］

根据相关研究［2，3，6］可知，影响多支路齿轮系统均载性能的因素主要包括啮合误差、耦合刚度、支撑刚度和转速，本文对功率分流式齿轮系统均载特性影响因素的分析主要从这几个方面展开。系统动力学方程在MATLAB软件中编程求解，采用四阶五级Runge-Kutta算法，调用ode45函数进行计算。

在分析啮合误差对系统均载特性的影响时，主要研究加工精度等级变化引起各齿轮副啮合误差幅值改变对系统均载性能的影响。如图3所示，计算得到了各齿轮副不同误差幅值变化时的均载系数曲线。

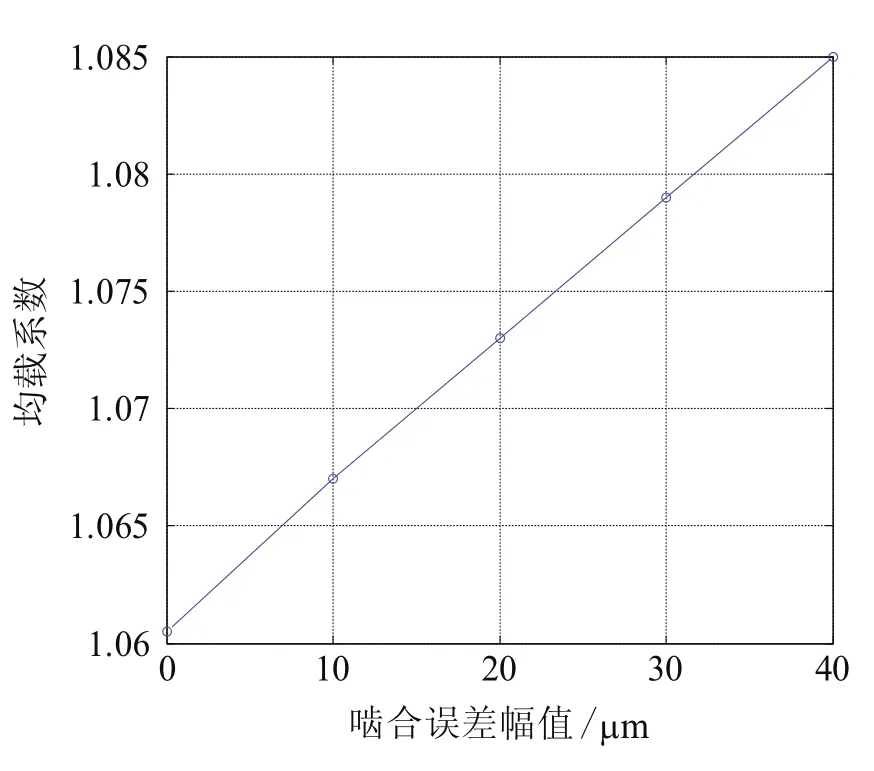
图3　不同误差幅值变化时的均载系数曲线

可以看出，随着系统中各齿轮副啮合误差幅值的增加，均载系数逐渐增大，均载性能变差，同时均载系数的增加呈近似线性递增的关系。值得注意的是，当各齿轮副啮合误差幅值为0时，即系统不存在误差，均载系数仍沿大于1，传动系统不均载，这一结果印证了Krantz指出该传动系统不均载是系统固有特性的观点。

功率分流式齿轮系统的耦合刚度主要指双联齿轮轴提供的大斜齿轮和小直齿轮间的扭转、弯曲和拉压刚度，某功率分流式齿轮系统的耦合刚度如表2所示。

计算得到耦合刚度大小变化时系统均载系数曲线如图4所示，图中横坐标为表2所示耦合刚度的倍数，为了更加有效的对结果进行分析，采用指数坐标。可以看出随着耦合刚度的增加系统均载系数逐渐增加，均载性能变差。当耦合刚度在现有耦合刚度附件变化时，系统均载系数变化率较大，随着耦合刚度变化增大，均载系数变化率逐渐减小，当耦合刚度接近现有耦合刚度0.1倍和10倍时，耦合刚度变化率接近于0。

由此说明，调节耦合刚度在一定范围时系统均载系数会发生较大变化，当耦合刚度过大或过小时，调节耦合刚度对均载系数的改变影响有限。

某功率分流式齿轮系统的支撑刚度如表3所示。计算得到支撑刚度大小变化时系统均载系数曲线如图5所示，横坐标为表3所示支撑刚度的倍数，同样采用指数坐标。可以看出随着支撑刚度的增加，系统均载系数逐渐减小，均载性能变好，随着支撑刚度的增加均载系数变化率逐渐减小。说明减小支撑刚度会引起均载系数较大变化，增加支撑刚度当达到一定程度时均载系数变化较小。

图4　不同耦合刚度变化时的均载系数曲线

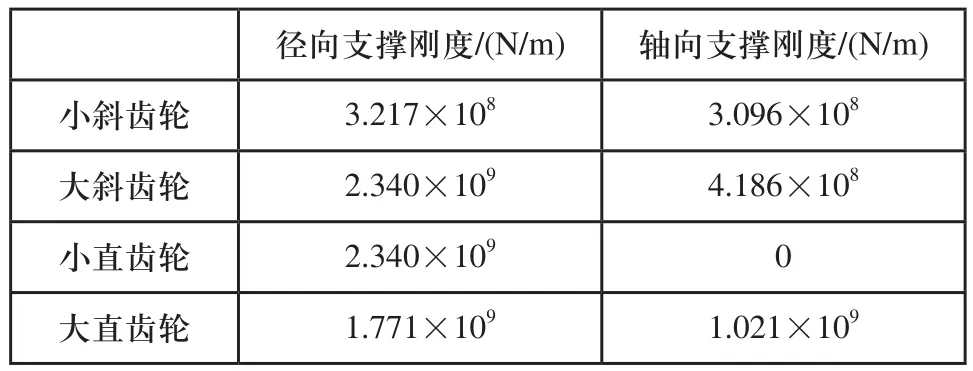
表3　某功率分流式齿轮系统支撑刚度

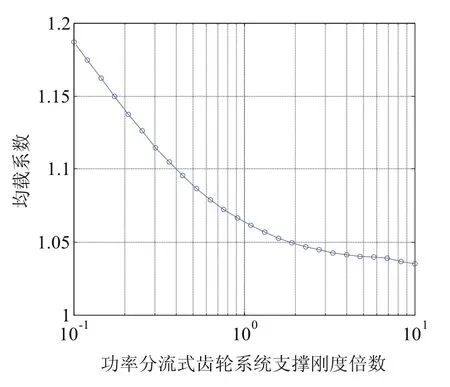
图5　不同支撑刚度变化时的均载系数曲线

计算得出系统不同工作转速时均载系数曲线如图6所示，图中横坐标为标准工作转速的倍数。可以看出系统均载系数对应于不同工作转速时无明显变化规律，当转速接近标准转速1.1倍时均载系数出现极大值，均载性能局部最优；当转速接近标准转速0.7倍时均载系数出现了极小值，均载性能局部最差。

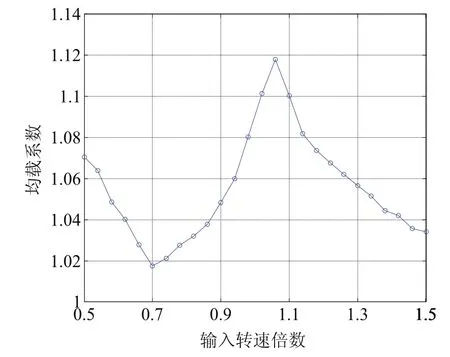
图6　不同转速变化时的均载系数曲线

5　结论

本文建立了功率分流式齿轮系统动力学模型，给出了系统动力学方程，分析了动力学模型中主要激励参数的计算方法。通过定义系统均载系数衡量均载性能，研究了误差、耦合刚度、支撑刚度和转速对系统均载的影响，得到以下结论。

1）减小啮合误差和耦合刚度、增大支撑刚度，以及选取合适的工作转速有利于提高功率分流式齿轮系统的均载性能。同时在一定范围内减小耦合刚度、增加支撑刚度均载性能能够得到快速提升。

2）对于功率分流式齿轮系统有效的均载方法包括：提高加工精度，设计合理结构使系统具有软耦合、硬支撑，选取合适工作转速。

［1］ J. G. Kish， Sikorsky Aircraft Advanced Rotorcraft Transmission（ART） Program-Final Report［Z］.NASA CR-191079，Cleveland: NASA Lewis Research Center，1993.

［2］ T. L. Krantz，Dynamics of a split torque helicopter transmission［Z］. NASA TM-106410， Cleveland: NASA Lewis Research Center，1994.

［3］ A. Kahraman， Load sharing characteristics of planetary transmissions［J］. Mechanism and Machine Theory，1994，29（8）:1151-1165.

［4］ Guo Y， Keller J， Lacava W.Combined effects of gravity， bending moment， bearing clearance， and input torque on wind turbine planetary gear load sharing［A］.American Gear Manufacturers Association［C］.2012.

［5］ H. Ligata， A. Kahraman，A.Singh， A closed-form planet load sharing formulation for planetary gear sets using a translational analogy［J］.Journal of Mechanical Design，2009，131（2）:021007-1-021007-7.

［6］ 付晨曦，赵宁，赵永志，等.基于FA-NSGA分扭传动系统的均载和轻量化优化设计［J］.航空动力学报，2014，29（9）:2247-2255.

［7］ Velex P，Ajmi M.Dynamic Tooth Loads and Quasi-Static Transmission Errors in Helical Gears-Approximate Dynamic Factor Formulae［J］.Mechanism and Machine Theory，2007，42（11）: 1512-1526.

Influence factor analysis of load sharing characteristic of power split gear system

YAO Lan1，ZHAO Bing2，XU Jing-wen2，LIU Xiao2，ZHOU Guo-tao2

TH132.41

A

1009-0134（2016）09-0050-04

2016-06-30

姚澜（1986 -），女，山东人，博士研究生，研究方向为传动系统设计与优化。