基于自组织随机权神经网络的BOD软测量

乔俊飞，鞠 岩，韩红桂

（北京工业大学电子信息与控制工程学院，北京 100124）

基于自组织随机权神经网络的BOD软测量

乔俊飞，鞠 岩，韩红桂

（北京工业大学电子信息与控制工程学院，北京 100124）

针对污水处理复杂系统中关键水质参数生化需氧量（biochemical oxygen demand，BOD）难以准确实时预测的问题，在分析污水处理过程相关影响因素的基础上，提出一种基于敏感度分析法的自组织随机权神经网络（selforganizing neural network with random weights，SONNRW）软测量方法.该方法首先通过机理分析选取原始辅助变量，经过数据预处理，之后采用主元分析法对辅助变量进行精选，作为SONNRW的输入变量进行污水处理关键水质参数BOD的预测.SONNRW算法利用隐含层节点输出及其权值向量计算该隐含层节点对于残差的敏感度，根据敏感度大小对网络隐含层节点进行排序，删除敏感度较低的隐含层节点即冗余点.仿真结果表明:该软测量方法对水质参数BOD的预测精度高、实时性好、模型结构稳定，能够用于污水水质的在线预测.

随机权神经网络；自组织；敏感度分析；软测量；生化需氧量（BOD）

现代经济社会的发展，给人们生活水平带来提高的同时，也对生态环境造成严重的破坏.其中污水处理成为环保领域的一个重要课题.作为污水处理过程出水水质重要参数，生化需氧量（biochemical oxygen demand，BOD）的准确、实时监测成为研究人员一直以来追求的目标.然而污水处理系统总是运行在非平稳状态，同时受制于传感器和检测仪表的精度、测量滞后以及环境污染等因素，BOD的高品质在线实时测控难以实现.

近年来，软测量技术作为一个强有力的工具被应用于工业过程的复杂系统建模中［1-2］.软测量技术采用的是间接测量的思想，使用容易测量的其他变量，构建模型来实现对难测变量的估计.而污水处理厂每天都会记录大量易测变量的运行数据，这就为污水处理过程软测量建模提供了便利的条件.软测量技术以其成本低、时效性和准确度高等特点，为污水处理过程出水BOD难以高品质实时监测的问题提供了一个有效的解决方案.

一些学者将基于统计与分析的软测量技术应用于污水处理建模过程，并取得了一定成效［3-4］.然而污水处理过程具有机理复杂、非线性强、难以建模等特点，基于统计与分析的软测量模型并不能很好地反映污水处理过程.而神经网络［5-7］凭借其可以逼近任意非线性函数及能够对复杂系统进行准确建模等优势，被广泛应用于污水处理过程建模的研究中［8-11］.张米娜等［12］以进水流量（Q）、进水化学需氧量（chemical oxyge demand，COD）的质量浓度、pH、固体悬浮物（suspended solids，SS）的质量浓度、总氮（total nitrogen，TN）的质量浓度为辅助变量，建立一个多输入单输出的三层前馈自适应增长修剪（adaptive growing and pruning，AGP）神经网络，采用反向传播（back propagation，BP）算法训练网络参数，对出水BOD进行预测，但是该方法网络学习算法简单，建立的软测量模型不够精确.王树东等［13］提出一种基于混合递阶遗传算法优化径向基函数神经网络（hybrid hierarchy genetic algorithm for radial basis function，HHGARBF）的BOD软测量方法，用递阶遗传算法（hierarchy genetic algorithm，HGA）来优化RBF神经网络的参数和拓扑结构，并能在全局范围内寻找RBF参数的最优解.该方法预测精度较高，但计算较为复杂.Islam等［14］提出一种自适应合并增长算法（adaptive merging and growing algorithm，AMGA），该算法在训练过程根据隐含层神经元的学习能力判断是否合并2个神经元或者增加1个新的神经元.然而该算法在网络训练过程中，每当删除或增加1个隐含层神经元，都需要对网络重新进行完整训练，计算较为复杂.

针对上述问题，一种算法简单、学习速度快、泛化能力好又不易陷入局部极小的单隐层前馈神经网络（single-hidden layer feedforward neural networks，SLFNs）随机权神经网络［15-18］（neural network with random weights，NNRW）进入研究人员的视野，并且成功应用于污水处理重要水质参数的软测量［19］.随机权神经网络在权值优化的过程中，隐含层节点参数随机选取，然后利用Moore-Penrose广义逆求最小二乘解的方法最终确定输出层权值，使得网络的训练转化为线性问题，从而避免了复杂的迭代过程，这就使得学习速度非常快成为NNRW算法最显著的特点.作为NNRW算法中唯一需要设定的参数，其隐含层节点个数的选取成为影响网络性能的关键因素.网络的隐含层节点个数过多会使得计算复杂，容易产生过拟合问题，影响神经网络的泛化性能［20-22］，反之会降低算法的学习能力，影响逼近能力.如何设计合理的算法来选取NNRW的隐节点个数成为网络结构优化设计的核心问题.

综上，本文提出了一种基于自组织随机权神经网络（self-organizing neural network with random weights，SONNRW）的污水处理BOD软测量方法.该方法利用污水处理过程机理分析结合先验知识确定辅助变量，进行数据预处理，并使用主元分析法（principal component analysis，PCA）对原始辅助变量精选，建立基于敏感度分析（sensitivity analysis，SA）法［23-25］的自组织随机权神经网络软测量模型，实现了对BOD的预测.经过仿真实验与对比，基于SONNRW的BOD软测量模型在预测出水BOD时能够在保持较高的预测精度的前提下，运算速度更快，泛化性能更强.

1　自组织随机权神经网络

1.1NNRW算法

假设N个不同的样本｛（xj，tj）|xj∈ RRn，tj∈ RRm，1≤j≤N｝.式中:xj=（xj1，xj2，…，xjn）T；tj=（tj1，tj2，…，tjm）T.隐含层节点个数为L，激活函数为G（x），则SLFNs的数学模型表示为

式中:1≤j≤N；ai为第i个隐节点输入权值；bi为其阈值；βi=（βi1，βi2，…，βim）T为第i个隐含层节点连接输出的权值向量；oj=（oj1，oj2，…，ojm）T为第j个样本对应的网络输出.

文献［15］已经证明，通过调节神经网络参数，单隐层神经网络可以以任意精度逼近训练样本，式（1）可改写为

H为SLFNs的隐含层输出矩阵，H的第i列表示第i个隐含层节点关于N个输入样本的输出；T为目标输出矩阵.

定义代价函数

传统算法是通过对参数ai、bi、β进行不断的迭代调整求解式（7）的最小化代价函数.Pao等在文献［15］中指出，输入层权值、阈值随机选取，只需调整输出层权值就可以使网络具有较好的逼近性能.只要激活函数无限次可微，输入层权值和阈值就可以随机选取，这就只需要找到适当的满足

所以当输入层权值和阈值随机选定，网络的隐层输出矩阵H就是已知的，式（3）的最小范数二乘解为

其中H†是H的Moore-Penrose广义逆.这种隐含层节点参数随机选取只求解输出层权值的方法称为随机权神经网络算法.

1.2基于敏感度分析法的随机权神经网络

敏感度分析法能够根据神经模型的输出来分析模型中的参数对输出的价值，从而根据期望值对网络参数进行修改调整，直到使神经网络输出达到期望值.敏感度分析法对于不同神经网络有不同的分析方法，但其基本思想是一致的［23-25］.

根据敏感度分析的思想，给出针对随机权神经网络的敏感度定义为

令

式中:i=1，2，…，L；j=1，2，…，N.

对于第j个训练样本，由式（1）可得

假设删除第i（1≤i≤L）个隐节点，则式（11）变为

将yj与y′j相减，可得残差

对于第j个样本，去掉第i个隐节点产生的误差为kij的绝对值与βi的模的乘积.因此可以定义:对于所有N个样本，残差相对于第i个隐节点的敏感度为

其中Ri越大，表明去掉第i个隐节点产生的残差越大，即第i个隐节点的重要性越强.因此，按照敏感度大小对隐含层节点进行排序，有

设阈值λ，令

则

式中L′为修剪后的隐节点个数.

关于阈值λ的选择问题，至今没有一个明确的方法.所以本文采用的方法是由λ=0.1开始，每次增加0.1，一直到1为止的试凑方式，选取网络性能最好时的λ来确定，操作较为方便.

为防止训练样本信息因隐含层神经元的删除而消失，本文采用权值横向平均传播的方法更新被保留节点的输入层权值，更新公式为

根据上述分析，下面给出基于敏感度分析的自组织NNRW算法的详细步骤如下.

步骤1 建立初始NNRW，选择足够大的初始隐含层节点数L，根据训练样本生成由L个隐含层节点组成的H矩阵，如式（4）（5）所示，L＜N.

步骤2 利用式（14）计算L个隐含层节点相对于残差的敏感度，按照敏感度大小对隐含层节点进行排序，有R′1≥R′2≥…≥R′L.

步骤3 确定阈值λ，由式（17）确定被删除节点.

步骤4 根据式（18）对删除冗余节点后的网络更新保留节点的输入权值.

步骤5 利用矛盾线性方程组的最小范数最小二乘解求得删除冗余点后网络输出层权值为

根据以上分析，删除了敏感度较低的隐含层节点，对网络预测精度影响较小，因此在满足训练精度的条件下，SONNRW算法能够得到结构更加紧凑的神经网络.

2　基于SONNRW的BOD软测量应用

建立出水BOD软测量模型主要可分为以下步骤:1）分析污水处理过程，选择与BOD关系密切的原始辅助变量；2）采集数据和预处理；3）精选输入变量；4）设计软测量模型结构.如图1所示.

2.1确定原始辅助变量

要想建立一个准确的BOD软测量模型，首先要找出污水处理过程中对BOD影响较大的参数，作为模型的原始辅助变量.这首先需要对污水处理运行系统进行机理分析.从污水处理工艺流程来看，污水处理系统属于高度复杂系统，包含多种生化反应，因此分析并找出在污水处理系统中与重要出水参数BOD关系密切的易测变量是建模的难点之一，也是准确地实现BOD软测量的关键因素之一.

以活性污泥法污水处理系统为研究对象，其主要由曝气池、二沉池、污泥回流系统、剩余污泥排放系统和供氧系统等组成.活性污泥是由细菌、菌胶团等多种微生物群体，悬浮物体，以及吸附的污水中有机性和无机性物质组成的絮绒状污泥，具有一定的活力.污水中的有机物正是被活性污泥吸附或通过生化反应被氧化分解，从而达到水质净化的目的.活性污泥法的生化反应主要发生在曝气池中.通过BOD的定义及检测方法可知，BOD表示的是污水中有机物等需氧污染物质质量浓度的一个综合指标.由此可知，影响微生物作用的因素也是影响BOD的因素有:Q、SS的质量浓度、曝气池溶解氧（dissolved oxygen，DO）的质量浓度、进水总磷（total phosphorus，TP）的质量浓度、TN的质量浓度、进水COD的质量浓度、曝气池氨氮（NH4-N）的质量浓度.另外，曝气池温度（T）、pH、氧化还原电位（oxidation-reduction potential，ORP）等参数也是活性污泥法污水处理系统的重要参数，会对微生物生存环境产生影响，进而影响微生物的生理活动，最终影响到BOD的值.同时在辅助变量选择方面，也可参考前人的先验知识，如文献［12］中张米娜等以Q、ρ（进水COD）、pH、ρ（SS）、ρ（TN）为辅助变量，作为软测量模型的输入变量，实现了对BOD的预测；文献［13］中王树东等以流量Q、ρ（进水SS）、曝气池ρ（DO）、T、pH、ρ（ORP）等作为辅助变量，进行BOD的预测.综合以上研究，通过机理分析和先验知识分析相结合的方法，最终将进水Q、ρ（SS）、ρ（COD）、ρ（TN）、ρ（TP）、曝气池ρ（NH4-N）、pH、T、ρ（ORP）、ρ（DO）这10个变量初步选择为原始辅助变量.各项辅助变量检测仪表见表1.

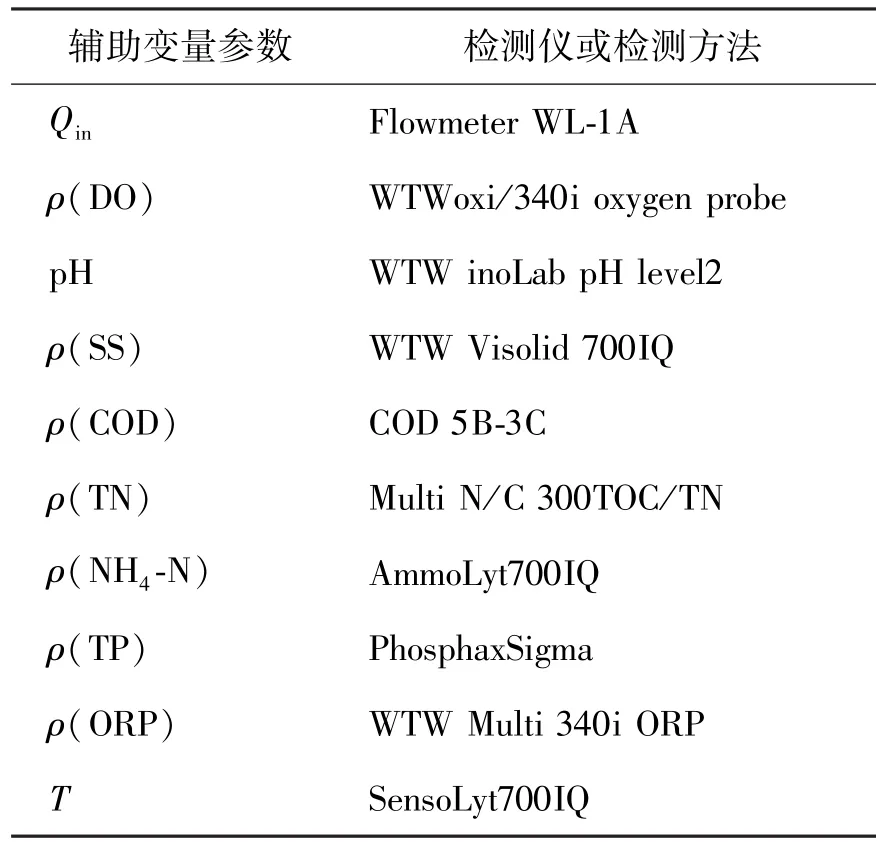
表1　辅助变量参数及其检测仪Table 1 Auxiliary variable parameter and detectors

2.2数据采集与预处理

对主导变量BOD和10个原始辅助变量的历史数据采集，主要通过安装在污水处理装置不同位置的传感器和变送器获得，且数量越大越好.然而受制于现场操作环境、仪器仪表测量精度、测量原理和方法等因素，所测得的数据难免会存在一定的误差.如果将这些包含误差的数据直接应用于BOD软测量，可能会严重影响软测量模型的性能，不仅不能准确预测主导变量，严重的还可能误导污水处理曝气、加药等操作，对整个污水处理系统产生影响，造成出水水质不达标等严重后果.因此，对所采集原始数据进行预处理以获得精确可靠的数据对软测量模型的建模和应用具有重要意义.原始数据的预处理主要包括剔除异常数据、填补缺失数据和数据归一化/反归一化处理.

2.2.1剔除异常数据

异常数据是指在数据测量和采集过程中，由于环境因素的影响、测量仪表的质量问题以及测量者数据录入错误等造成的异常的数据结果.一般多采用一种简单又常用的统计判别法3σ准则来对原始辅助变量和主导变量中的异常数据进行剔除.

设N个数据样本（x1，x2，…，xN），均值为χ，每个样本的偏差为D（j）=x（j）-x，j=1，2，…，N，计算标准偏差

若x（j）的偏差满足

则认为x（j）是异常数据，应予以剔除.

2.2.2缺失数据的插值填补

由于某些数据可能会在测量过程或传输过程中丢失，因此会出现测量到的某些数据出现缺失的情况.针对这个问题，本文采取的是线性插值的方法来填补缺失数据，具体方法为:

在t-1，t，t+1时刻的采样点分别为（at-1，bt-1，ct-1，…）、（at，bt，ct，…）、（at+1，bt+1，ct+1，…），假设t时刻样本中某一变量at丢失，则

若出现连续2个或数个时刻数据丢失的情况，则根据这几个时刻的前后时刻所测数据进行均分插值填补.这样不但尽可能在一定误差范围内填补了缺失数据，同时还保证了数据的平滑性.

2.2.3数据的归一化/反归一化处理

为了消除污水处理过程中参数不同量纲的影响，需要对软测量数据进行归一化和反归一化处理.具体为最大最小化法，计算公式为

式中:i=1，2，…，10；输入变量x=［Qin、ρ（DO）、pH、ρ（SS）、ρ（COD）、ρ（TN）、ρ（NH4-N）、ρ（TP）、ρ（ORP）、T］T；x′i是第i维变量归一化后的值；xi，min是第i维变量的最小值；xi，max是第i维变量的最大值.

2.3精选辅助变量

在污水处理过程建模中，数据种类越多，其中包含的信息也就越多，对建模的准确性也越有帮助.但如果辅助变量个数太多，可能会导致测量的噪声也随之增大，同时所建立软测量模型的复杂度变高，继而其模型适应性就会降低，限制模型的应用.本文采用PCA方法分析各原始辅助变量与主导变量的关系，删除冗余辅助变量，使得精选出的少量辅助变量可以最大化表达原始数据信息.PCA方法的主要思想是通过对数据的统计分析，得出输入变量与输出变量之间的关联度并加以排序，从而精选出辅助变量，达到降维的目的.

PCA方法常用计算步骤如下.

1）样本矩阵为XN×I，其中共有I维样本变量，N个样本，本文中I=10，代表10个原始辅助变量.

2）计算X的协方差矩阵

3）求解协方差矩阵CX的I个特征值λ1≥λ2≥…≥λI和相对应的特征向量p1，p2，…，pI.

4）按由大到小顺序将特征值进行排列，并按照

计算前n个主元的累积贡献率.

5）取前n个较大的特征值所对应的特征向量构成变换矩阵PT:PT=（p1，p2，…，pn），n＜I.

6）通过Y=PX计算前n个主成分，达到降低维数、精选辅助变量的目的.

本文使用历史数据，通过主元分析法计算10个原始辅助变量的累计方差贡献率，以η＞0.85为指标，最终精选出了BOD软测量模型的4个辅助变量，即网络的输入为ρ（SS）、ρ（COD）、pH、ρ（DO），如表2所示.

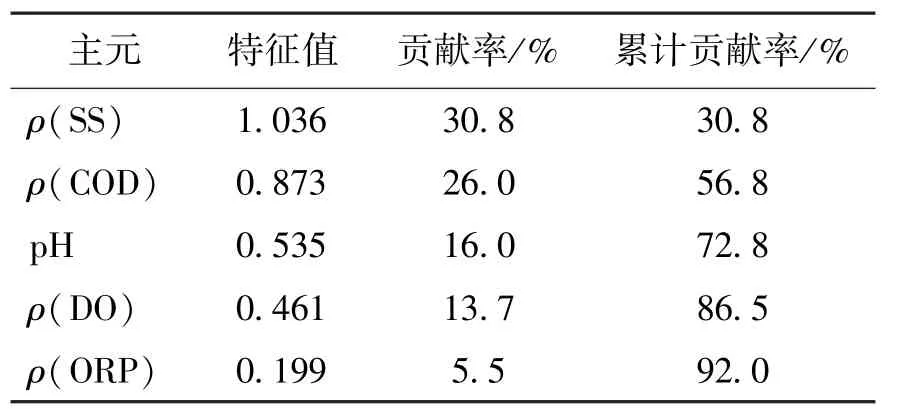
表2　不同主元贡献率Table 2 Variances of principle components

2.4软测量模型结构设计

出水BOD软测量模型选取的是上文所述的自组织随机权神经网络SONNRW.软测量模型的输入为降维后的4组辅助变量ρ（SS）、ρ（COD）、pH、ρ（DO），并通过SONNRW预测出水BOD的实时数值，如图2所示.SONNRW的隐含层节点激活函数选择Sigmoid函数，初始隐含层个数L选取要足够大，具体要根据实验样本的多少进行设定.

BOD软测量算法步骤如下:

步骤1 建立初始NNRW，模型输入为ρ（SS）、ρ（COD）、pH、ρ（DO），输出为ρ（BOD），选择足够大的初始隐含层节点数L，根据训练样本生成由L个隐含层节点组成的H矩阵.

步骤2 利用式（14）的敏感度分析法计算L个隐含层节点相对于残差的敏感度，按照敏感度大小对隐含层节点进行排序.

步骤3 确定阈值λ，由式（17）确定被删除节点.

步骤4 根据式（18）对删除冗余节点后的网络更新保留节点的输入权值.

步骤5 利用矛盾线性方程组的最小范数最小二乘解求得删除冗余点后网络输出层权值.

步骤6 使用训练样本对网络进行训练.

步骤7 确定网络和参数后，使用训练的网络对BOD进行预测.

3　仿真实验

本文的仿真实验分为2个部分.首先将SONNRW应用于非线性动态系统辨识中来验证SONNRW的性能，确定其在非线性动态系统辨识中具有良好的辨识效果后，再将其应用于污水处理BOD预测中，并通过与原始NNRW［15］以及AGPBP［12］、HHGARBF［13］、AMGA［14］算法进行对比来验证该算法的性能.所有实验运行于Matlab R2012a版本，操作系统为Win7，电脑硬件配置为酷睿2 Duo 2.94 GHz CPU、4 G RAM.

3.1非线性动态系统辨识

首先利用SONNRW对非线性系统进行辨识，通过与一些常用算法比较来证明本算法的性能.所采用的非线性动态系统为

式中:y（0）=0；y（1）=0；u（t）=sin（2πt/25）.

模型可以表示为

（y（t），y（t-1），u（t））作为SONNRW的3个输入变量，输出变量为y（t+1）.实验共采用500组数据，其中前400组作为训练样本，后100组用作测试样本.初始隐含层神经元为12个，迭代步数为1 000步，目标训练误差为0.01.

经SONNRW算法对网络进行训练，隐含层神经元数量变化如图3所示，最终个数为8.图4为SONNRW训练曲线图，图5为SONNRW对非线性动态系统的辨识效果，图6为误差曲线，与原始NNRW以及AGPBP和AMGA算法的详细对比结果如表3所示.

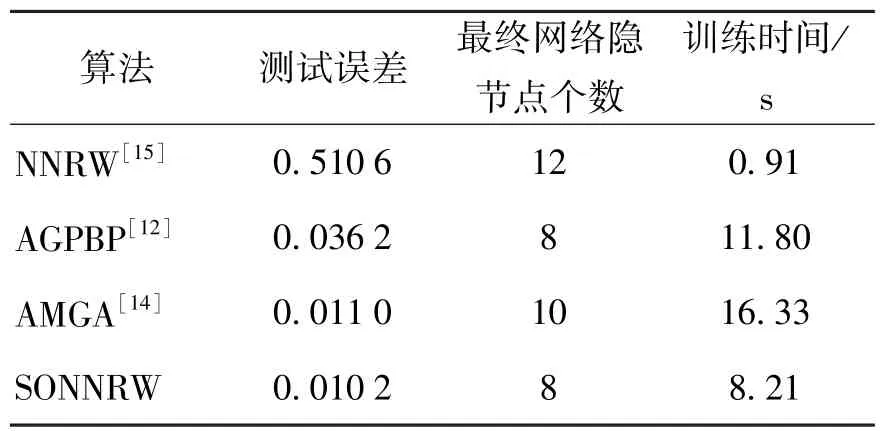
表3　4种网络性能对比Table 3 Comparison of 4 networks'performance

从表3可以看出，原始NNRW没有结构优化能力，虽然在运算速度方面非常快，但精度较低.SONNRW算法能够获得精简的网络结构，训练后隐含层节点个数与AGPBP算法相当，但测试精度更高.同AMGA算法相比具有相似的测试精度，但SONNRW有更精简的网络结构和更快速的训练速度.

从图5、6可以看出，SONNRW能够较好地对非线性动态系统进行辨识，具有较高的辨识精度，说明SONNRW不仅能够获得精简的网络结构，同时还有着良好的泛化性能.

3.2出水BOD软测量应用

为了进一步验证SONNRW用于BOD软测量系统的有效性，实验使用污水处理厂真实数据进行仿真实验.在仿真实验中，利用SONNRW及其他结构调整算法对污水处理BOD进行预测，同时将预测数据与真实数据进行对比，计算各算法的预测精度及性能.

选取来自于北京市某污水处理厂2014年9月的数据120组，剔除异常数据5组，随机选择其中60组用于神经网络的训练，40组用于网络的预测.初始隐含层个数设置为L=20，使用SONNRW的算法流程对前60组数据进行训练，目标训练误差0.01，迭代步数为1 000步，对后40组数据进行预测，同时记录训练时间、测试误差.所有实验在相同条件下重复20次，取平均值.经过训练之后的SONNRW隐含层神经元个数为10个.

图7为自组织随机权神经网络训练过程误差变化曲线，可以看出，SONNRW可以快速收敛到稳定状态.图8为出水水质BOD训练效果图，训练误差如图9所示，图10为出水水质BOD预测效果图，预测误差如图11所示.

从图8、10可以看出，不论是训练效果还是预测效果，SONNRW都能达到较好的拟合精度，说明利用基于SONNRW的软测量方法对出水水质BOD进行训练与预测时，可以达到较高的训练精度和预测精度，能够很好地预测出水BOD的值.从图9、11可以看出，训练误差保持在［-0.4，0.4］，测试误差保持在［-0.8，0.8］，表明该软测量模型具有较好的稳定性和泛化性能.

与原始NNRW及其他几种结构调整神经网络的详细比较如表4所示.可以看出，原始NNRW没有自组织能力，虽然训练时间快，但误差较大；SONNRW加入结构调整机制后，虽然牺牲了部分训练速度，但在精简网络规模和提高泛化能力方面都有较大的提升.SONNRW算法与AGPBP［12］和HHGARBF［13］算法相比，测试精度和训练速度都有所提高，网络规模也得到了较好的控制，对污水处理BOD软测量中表现出了良好的性能.

表4　4种网络在BOD软测量中的性能对比Table 4 Comparison of four networks'performance in BOD soft-sensing

4　结论

本文针对污水处理复杂系统重要参数BOD难以实时准确测量的问题，提出一种基于敏感度分析的SONNRW软测量模型.首先使用非线性动态系统辨识的方法来验证SONNRW的性能，再使用污水处理真实数据进行BOD预测仿真实验来验证本方法的有效性.通过与几种常用结构调整神经网络软测量方法进行对比，得出以下结论:

1）SONNRW算法能够在保证较高测试精度的前提下，构建结构紧凑的神经网络.

2）与AGPBP算法、AMGA算法和HHGARBF算法对比，SONNRW具有更快的学习速度、更加紧凑的网络结构和更好的泛化性能.

3）基于SONNRW的软测量方法能够利用ρ（SS）、ρ（COD）、pH、ρ（DO）对污水处理过程重要参数ρ（BOD）实现较为准确有效的预测，具有精度高、实时性好、稳定性好等特点，在解决污水处理过程重要水质参数的软测量问题上具有较好的实用价值.

［1］XU F，WANG Y Y，LUO X L.Soft sensor for inputs and parameters using nonlinear singular state observer in chemical processes［J］.Chin J Chem Eng，2013，21（9）: 1038-1047.

［2］SHAO W M，TIAN X M，WANG P.Local partial least squares based online soft sensing method for multi-output processes with adaptive process states division［J］.Chin J Chem Eng，2014，22（7）:828-836.

［3］DI M C，SAUNDERS A C G.Nonlinear estimation and control of mycelia fermentations［C］//American Control Conference.Pittsburgh，PA:IEEE，1989:1994-1999.

［4］MCACVOY T J.Contemplative stance for chemical process control［J］.Automatica，1992，28（2）:441-442.

［5］乔俊飞，韩红桂.RBF神经网络的结构动态优化设计［J］.自动化学报，2010，36（6）:865-872.QIAO J F，HAN H G.Optimal structure design for RBFNN structure［J］.Acta Automatic Sinica，2010，36（6）:865-872.（in Chinese）

［6］HAN H G，QIAO J F.A structure optimization algorithm forfeedforwardneuralnetworkconstruction［J］.Neurocomputing，2013，99（1）:347-357.

［7］QIAO J F，LI F J，HAN H G，et al.Constructive algorithm for fully connected cascade feedforward neural networks［J］.Neurocomputing，2016，182:154-164.

［8］赖惠鸽，朱学军，俞金寿.基于智能算法的污水处理软测量技术及其展望［J］.化工自动化及仪表，2011，38（3）:241-244.LAI H G，ZHU X J，YU J S.Research on intelligent algorithm-basedsoft-sensingtechnologyforsewage treatment process［J］.ControlandInstrumentsin Chemical Industry，2011，38（3）:241-244.（in Chinese）

［9］YUAN X C，HAN H G，QIAO J F.The sludge volume index soft sensor model based on PCA-ElmanNN［C］//IEEE International Joint Conference on Neural Networks.Brisbahe:IEEE，2012:1-7.

［10］LIN F J，CHEN S Y，TENG L T C.Recurrent functionallink-based fuzzy neural network controller with improved particle swarm optimization for a linear synchronous motor drive［J］.IEEE Transactions on Magnetics，2009（8）: 3151-3165.

［11］HUANG M Z，MA Y W，WAN J Q，et al.A sensorsoftware based on a genetic algorithm-based neural fuzzy systemformodellingandsimulatingawastewater treatment process［J］.Appl Soft Comput，2015，27（1）: 1-10.

［12］张米娜，韩红桂，乔俊飞.前馈神经网络结构动态增长-修剪方法［J］.智能系统学报，2011，6（2）:101-106.ZHANG M N，HAN H G，QIAO J F.Research on dynamic feed-forward neural network structure based on growing and pruning method［J］.CAAI Transactions on Intelligent Systems，2011，6（2）:101-106.（in Chinese）

［13］王树东，葛珉昊，陈明明.基于混合递阶遗传算法优化RBF神经网络的BOD5软测量方法［J］.计算机技术，2014（3）:149-153.WANG S D，GE M H，CHEN M M.BOD5 soft measurement basedonHHGA-RBF［J］.Computer Technology，2014（3）:149-153.（in Chinese）

［14］ISLAM M M，SATTAR M A，AMIN M F，et al.A new adaptive merging and growing algorithm for designing artificial neural networks［J］.IEEE Transactions on Systems，Man，and Cybenetics—Part B:Cybernetics，2009，39（3）:705-722.

［15］PAO Y H，PARK G H，SOBAJIC D J.Learning and generalizationcharacteristicsoftherandomvector Functional link net［J］.Neurocomputing，1994（6）: 163-180.

［16］IGELNIK B，PAO Y H.Stochastic choice of basis functions in adaptive function approximation and the functional-link net［J］.Neural Networks，1995，6（6）: 1320-1329.

［17］CAO F L，YE H，WANG D H.A probabilistic learning algorithm for robust modeling using neural networks with random weights［J］.Inf Sci，2015，313:62-78.

［18］DAI W，LIU Q，CHAI T Y，Particle size estimate of grinding processes using random vector functional link networks with improved robustness［J］.Neurocomputing，2015，169:361-372.

［19］ZHAO L J，YUAN D C，CHAI T Y.KPCA and ELM ensemble modeling of wastewater effluent quality indices.Procedia Engineering［J］.2011，15（1）:5558-5562.

［20］MAN Z，LEE K，WANG D H.A new robust training algorithm for a class of single-hidden layer Feed forward neural networks［J］.Neurocomputing，2011，74（16）: 2491-2501.

［21］HAN H G，QIAO J F.A self-organizing fuzzy neural network based on a growing-and-pruning algorithm［J］.IEEE Trans Fuzzy Syst，2010，18:1129-1143.

［22］SALTELLI A，RATTO M，TARANTOLA S，et al.Sensitivity analysis practices:strategies for model-based inference［J］.ReliabilityEngineeringandSystems Safety，2006，91（10/11）:1109-1125.

［23］HAN H G，QIAO J F.A structure optimization algorithm forfeedforwardneuralnetworkconstruction［J］.Neurocomputing，2013，99:347-357.

［24］CARIBONG J，GATELLI D，LISKA R，et al.The role of sensitivity analysis in ecological modeling［J］.Ecological Modelling，2007，203（1/2）:167-182.

［25］CAMPOLONGO F，CARIBONJ J，SALTELLI A.An effective screening design for sensitivity analysis of large models［J］.Environmental Modelling and Software，2007，22（10）:1509-1518.

（责任编辑 吕小红）

BOD Soft-sensing Based on SONNRW

QIAO Junfei，JU Yan，HAN Honggui
（College of Electronic Information and Control Engineering，Beijing University of Technology，Beijing 100124，China）

Aiming at the problem that biochemical oxygen demand（BOD）soft-sensing is difficult to be forecasted accurately and in real time，a self-organizing neural network with random weights（SONNRW）is proposed by using the sensitivity analysis method.Firstly，we select the original auxiliary variables using mechanism analysis，then we use PCA method to select variables after the data preprocessing.The selected variables are the input SONNRW to forecast the key water quality parameter BOD.The residual error's sensitivities to the hidden nodes are defined by their outputs and weight vectors connecting to the out layer using the sensitivity analysis method.First，we calculate the sensitivities by using the hidden layer outputs and the responding output layer weight vectors.Then the orders are sorted based on the sensitivity of each hidden node.Then those nodes which have lower sensitivities will be pruned by using the Leave-one-out method.By using this method in BOD soft-sensing，experiments show that the pruning NNRW has high prediction accuracy，more streamlined network size andbetter generalization performance.

neural networks with random weights；self-organizing；sensitivity analysis method；softsensing；biochemical oxygen demand（BOD）

TP 183

A

0254-0037（2016）10-1451-10

10.11936/bjutxb2016040021

2016-04-07

国家自然科学基金资助项目（61533002）；中国博士后科学基金资助项目（2015M570911）；北京市科技新星计划项目（Z131104000413007）

乔俊飞（1968—），男，教授，博士生导师，主要从事智能信息处理、智能优化控制方面的研究，E-mail:junfeiq@ bjut.edu.cn