受恶意程序传染的WSNs可生存性评估*

沈士根，黄龙军，范　恩，胡珂立，刘建华，曹奇英

（1.绍兴文理学院计算机科学与工程系，浙江绍兴312000；2.嘉兴学院数理与信息工程学院，浙江嘉兴314001；3.浙江工业大学计算机科学与技术学院，杭州310023；4.东华大学计算机科学与技术学院，上海201620）

受恶意程序传染的WSNs可生存性评估*

沈士根1，2*，黄龙军1，3，范恩1，胡珂立1，刘建华2，曹奇英4

（1.绍兴文理学院计算机科学与工程系，浙江绍兴312000；2.嘉兴学院数理与信息工程学院，浙江嘉兴314001；3.浙江工业大学计算机科学与技术学院，杭州310023；4.东华大学计算机科学与技术学院，上海201620）

为实现传感节点数据高可靠传输的无线传感器网络WSNs（Wireless Sensor Networks），提出一种针对受恶意程序传染的聚簇WSNs可生存性评估方法。通过使用能预测恶意程序传染行为的博弈模型，将恶意程序传染的故意性与马尔可夫链的随机性关联，实现利用马尔可夫链中的状态转换描述恶意程序传染行为的目的。使用提出的易感节点可靠度评估指标，根据可靠性理论将聚簇WSNs看作一个“并-串-并”系统，推理得到了一个簇、一条路由直至整个WSNs的可靠度评估指标，最终得到WSNs生存期评估指标。实验分析了影响WSNs可生存性的因素，结果表明提出的方法能有效评估WSNs的可生存性，为设计高可生存的WSNs提供理论基础。

无线传感器网络；可生存性评估；博弈论；恶意程序传染；可靠性理论

EEACC:7230doi:10.3969/j.issn.1004-1699.2016.07.022

无线传感器网络 WSNs（Wireless Sensor Networks）安全是实现环境监测、目标跟踪、健康检测等众多应用的保障，因此备受学术和工业界的关注［1-5］。其中，网络可生存性作为WSNs安全的重要组成部分，表示WSNs即使在面临恶意程序攻击或自然灾害的情况下，都要求WSNs具有可靠和可用的能力。而要能利用各种可生存技术提高WSNs的可生存性，可生存性评估是前提，同时，得到的评估结果能为高可生存的WSNs设计提供最优解决方案。

近期研究［6］表明，在WSNs中容易传染恶意程序。一方面，组成同一个WSNs的传感节点的软硬件具有同构性，一旦有一个传感节点被恶意程序感染，就容易扩散恶意程序到整个网络。另一方面，对那些部署后不能再人工操作的传感节点，目前主要使用如Trickle、Firecracker等协议对其进行重配置或重编程，实现传感节点系统软件分发和更新功能，但恶意攻击者也可使用这些协议传染恶意程序。因此，对受恶意程序传染的WSNs进行可生存性评估已逐渐成为当前WSNs安全性研究的热点。

目前，国内外研究者已提出了一些与WSNs相关的可生存性评估方法。徐恪等人［7］对互联网体系结构的评估模型及方法的综述为WSNs可生存性评估提供了很好的借鉴作用。王海涛等人［8］通过筛选应急通信中WSNs的可生存性评估指标，提出了基于网络分析法的评估模型。朱世才等人［9］利用半马尔可夫过程针对聚簇WSNs建立了可生存性评估模型，而熊书明等人［10］利用半马尔可夫过程对WSNs的拓扑容侵进行了定量评估，这种方法还被用于混合余度传感器系统的可靠性建模与分析［11］。刘文芬等人［12］基于马尔可夫博弈模型提出了一种优化的网络风险评估方法。Parvin等人［13］利用连续时间马尔可夫链分别建立了受攻击和密钥泄露环境下的WSNs可生存性评估模型。Petridou等人［14］采用概率模型检测（Probabilistic Model Checking）技术从错误发生率、数据丢失率、数据延迟率、数据泄露率4个方面评估WSNs的可生存性。Zhang等人［15］提出了基于随机Petri网的WSNs可生存性评估方法。与WSNs可生存性评估密切相关的还有WSNs可靠度评估。Cai等人［16］针对事件驱动WSNs，分别从无线链接可靠度和节点能量可用度两方面评估网络的可靠度。其他的典型方法还包括结合可靠性框图和Petri网的方法［17］、基于随机活动网络的方法［18］等。

由于恶意程序的传染与流行病传染有相似的特性，因此流行病模型是一种常用的WSNs恶意程序传染建模方法。通常，在使用流行病模型时，会定义传感节点所处的不同状态，如易感（Susceptible，S）、已感染（Infected，I）、恢复（Recovered，R）等。再根据这些不同的状态，得到相应的流行病模型，如经典的SI［19］、SIS［20］、SIR［21］等模型以及扩展的SEIRS（Susceptible-Exposed-Infected-Recovered-Susceptible）［22］模型和SIRD（Susceptible-Infected-Recovered-Dead）［23］模型。

马尔可夫链作为一种随机过程，在描述状态转换方面具有卓越的能力。然而，仅使用马尔可夫链很难表达受恶意程序传染时的传感节点状态，这是由于恶意程序在向易感节点传染恶意程序时常常是故意的，使得这种传染行为导致的传感节点状态变换不能用随机过程进行描述。这个问题通过引入能预测恶意程序期望传染概率的策略博弈可以得到解决。

本文利用流行病理论、可靠性理论、博弈论、马尔可夫链等理论，提出一种针对受恶意程序传染的WSNs可生存性评估方法。首先，根据聚簇WSNs中传感节点的通信特性，将整个WSNs映射到一个“并-串-并”系统，从而可以利用可靠性理论评估整个WSNs的可靠度。其次，通过建立“恶意程序传染博弈”模型预测恶意程序的传染行为，得到恶意程序的最优传染策略，并将其应用于恶意程序传染模型向马尔可夫链的转化过程。最后，受经典可靠性评估指标的启发，提出一种能反映易感节点的可靠度评估指标，并依次建立了一个簇、一条路由和整个WSNs的可靠度以及整个WSNs生存期等评估指标，实现WSNs可生存性评估机制。

1　网络模型

由于聚簇WSNs应用的普遍性，本文选择聚簇WSNs研究其可生存性。在这种聚簇WSNs中，不同区域的传感节点被分配到不同的簇中。每个簇包含一个簇头和若干普通传感节点。一个普通传感节点获得感知数据后，将向所在簇的簇头发送数据，簇头融合数据后通过其他一个个相邻的簇头将数据传输到基站，为了平衡簇头节点数据融合和信号发送产生的能量消耗，担任簇头责任的节点会定期更新。

聚簇WSNs和经典可靠性理论中的“串-并”系统存在天然的映射关系。聚簇WSNs中的传感节点相互独立，也就是说，一个传感节点有故障不会影响其他传感节点。这样，可以借助经典可靠性理论研究传感节点的可靠度，进而给出一个簇、一条路由乃到整个WSNs的可靠度。而且，一个簇中有多个可选的簇头节点，若当前簇头节点因恶意程序传染导致故障时，系统会从候选簇头节点中选举出新的簇头，所以一个簇中只要有一个候选簇头节点还能发送数据，那么该簇即能发送数据。因此，由候选簇头和普通传感节点组成的簇就能映射到经典可靠性理论中的一个并行系统。对于从源传感节点经其他簇头转发数据到基站的一条路由，只有经过的所有簇头能正常工作，数据才能被正常传输到基站。因此，由多个簇头组成的路由就能与经典可靠性理论中的一个串行系统相对应。对于整个WSNs而言，从源传感节点传输数据到基站的路由数有多条，显然，整个WSNs可以与一个并行系统相对应。综合上述分析，整个WSNs实质是一个“并-串-并”系统，如图1所示。

图1　基于“并-串-并”系统的聚簇WSNS结构

2　恶意程序传染模型及传染行为预测

2.1基于流行病理论的恶意程序传染模型

利用流行病理论建立的恶意程序传染模型实质是一种状态转换模型。对一个传感节点而言，在某个时间点的状态是确定的，并且在传感节点的整个生命期内，传感节点的状态会不断变化，形成状态空间。例如，系统通过安装安全补丁来修复易感节点上的漏洞使它免受已知恶意程序的感染是一种通用的安全技术，这种技术实质是将传感节点的易感状态S转换到被感染状态I。因此，系统或恶意程序采取的不同行为将导致传感节点的状态转化。

图2给出了从易感状态S转换到被感染状态I的部分马尔可夫链，其中ρI表示恶意程序选择“传染”动作的概率，λ表示成功感染一个易感节点的概率。这样，恶意程序感染一个易感节点的行为转变成了马尔可夫链中的一个状态转换。接下来，我们通过建立一个策略博弈来预测恶意程序期望的传染行为，即得到ρI。

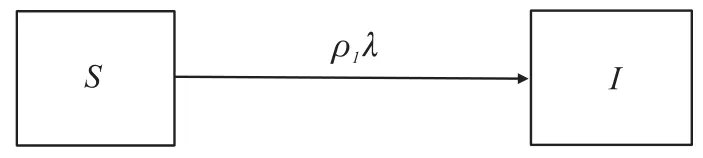
图2　传感节点从状态S转换到I的部分马尔可夫链

2.2基于博弈论的恶意程序传染行为预测

定义1“恶意程序传染博弈”模型是一个四元组G=（N，AM，AS，U），其中：N=｛恶意程序，WSNs系统｝表示参与者集合；AM=｛Infect，Non-infect｝表示参与者“恶意程序”可选择的动作集合；AS=｛Defend，Non-defend｝表示参与者“WSNs系统”可选择的动作集合；U:AM×AS↦ℝ表示两个参与者选择不同动作产生的支付矩阵。

在定义1中，参与者“恶意程序”代表了WSNs中众多的恶意程序，通过感染易感节点能窃听私密的传感节点数据、影响传感节点间的通信等。“WSNs系统”实质是驻留在WSNs中的入侵检测系统IDS（Intrusion Detection System）。图3给出了参与者“恶意程序”和“WSNs系统”之间的博弈过程。

图3　参与者“恶意程序”和“WSNs系统”之间的博弈过程

记ρI和ρϕ是参与者“恶意程序”分别选择动作Infect和Non-infect的概率，δD和δϕ是参与者“WSNs系统”分别选择动作Defend和Non-defend的概率。在图3中，“恶意程序”采取的感染策略ρ实际上是一个混和策略（ρI，ρϕ），表示在动作集合AM上的概率分布，即ρ=（ρI，ρϕ）且满足ρI+ρϕ=1。其中，感染概率ρI代表了恶意程序实施动作Infect的程度，其值越大，一个易感节点被感染的概率越大。同理，“WSNs系统”采取的防御策略δ表示在其动作集合AS上的混合策略，即δ=（δD，δϕ）且满足δD+δϕ=1。

为描述“恶意程序传染博弈”的支付矩阵，记ω（ω＞0）为一个传感节点感知数据的价值，cI为恶意程序感染易感节点的成本，cD为WSNs系统防御恶意程序感染节点的成本，α、β、γ分别为IDS的检测率、误报率、漏报率。当恶意程序成功感染易感节点时，恶意程序将获得收益ω，而WSNs系统损失ω；当WSNs系统成功防御恶意程序的感染行为时，由于它保护了价值为ω的易感节点，因此获得收益ω而恶意程序损失ω。

考虑IDS的检测率、误报率、漏报率，若恶意程序和WSNs系统采取“纯策略对”（Infect，Defend），对恶意程序而言，不能被IDS成功检测和IDS漏报分别得到收益（1-α）ω和γω，被IDS成功检测产生损失αω。因此，其支付

对WSNs系统而言，成功检测恶意程序得到收益αω，不能成功检测恶意程序和漏报恶意程序分别产生损失（1-α）ω和γω。因此，其支付

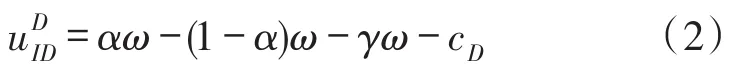
若恶意程序和WSNs系统采取“纯策略对”（Infect，Non-defend），恶意程序的支付

而WSNs系统的支付

若恶意程序和WSNs系统采取“纯策略对”（Noninfect，Defend），恶意程序的支付

而WSNs系统的支付

其中，βω表示IDS误报恶意程序产生的损失。若恶意程序和 WSNs系统采取“纯策略对”（Noninfect，Non-defend），显然，恶意程序和WSNs系统的支付都为0。综上分析，可得“恶意程序传染博弈”的支付矩阵如表1所示。

表1　“恶意程序传染博弈”的支付矩阵

在“恶意程序传染博弈”模型中，恶意程序的目标是最大化其感染易感节点的期望效用，而WSNs系统的目标是最大化防御恶意程序的期望效用。由于任何一个有限的策略博弈都存在混合策略纳什均衡点，因此，上述目标可以通过求解博弈模型的纳什均衡点实现。

实际计算时，首先根据支付矩阵分别表示出恶意程序选择动作Infect和Non-infect的期望支付，再由达到纳什均衡时恶意程序选择动作Infect和Non-infect的无差异性（Indifference），可得到恶意程序最优传染策略。此时，恶意程序将获得最大期望收益，因此，恶意程序没有理由不选择最优传染策略 ρ∗进行传染。这样，将代替图2中的ρI，从而使恶意程序传染的故意性能通过马尔可夫链进行描述。

3　可生存性评估机制

通常，评估一个系统的可生存性，从评估该系统的可靠度入手。平均故障时间MTTF（Mean Time to Failure）和平均故障间隔时间MTBF（Mean Time between Failure）是评价一个系统可靠度的典型指标。其中，MTTF反映一个系统能可靠运行的时间，而MTBF反映一个系统相邻的两次故障的平均时间。因此，MTTF和MTBF分别用于评估不可修复和可修复组件的可靠度评估。由于传感节点一旦被破坏就很难修复，因此，文献［24-25］都用MTTF评估一个传感节点的可靠度。

本文受MTTF启发，为反映WSNs中一个易感节点的可靠度，提出一种新的可靠度评估指标MTTI（Mean Time to Infection，平均感染时间）。图2中的ρIλ反映了一个易感节点被恶意程序感染的概率，其值越大，一个易感节点越容易被感染。因此可以关联ρIλ到一个易感节点的MTTI中来得到相应的定义。

定义2受恶意程序传染的WSNs中，一个易感节点的MTTI为

定义3受恶意程序传染的WSNs中，一个易感节点i的可靠度Ri（t）为

由聚簇WSNs和经典可靠性理论中“串-并”系统的映射关系，一个簇对应一个并行系统，一条路由对应一个“串-并”系统，整个WSNs对应一个“并-串-并”系统。所以，一个簇j的可靠度Rj（t）为

其中，m表示一个簇中的可选簇头数。一条路由k的可靠度Rk（t）为

其中，n表示一条路由包含的簇数。整个聚簇WSNs的可靠度R（t）为

其中，l表示整个WSNs中可选的路由数。从而，整个WSNs的生存期T为

4　实验

使用实验工具Matlab R2010b，首先说明IDS的检测率、误报率、漏报率对一个易感节点MTTI的影响，再从整个WSNs的生存期说明本文提出的可生存性评估方法的有效性。实验参数设定λ=0.1，ω=12，cD=2，cI=4。值得说明的是，这些参数值的改变会影响一个易感节点的MTTI值和整个WSNs的生存期，但整个数据曲线变化趋势不变。

4.1易感节点MTTI的影响因素

IDS较高的检测率、较低的误报率和漏报率能使IDS更容易地检测到恶意程序，从而可使WSNs系统采取措施抑制恶意程序的传染。因此，随着检测率的提高、误报率和漏报率的降低，恶意程序的最优传染策略是减小选择动作Infect的概率，以降低被IDS捕获的概率，这样就使得一个易感节点MTTI值逐渐升高。

图4给出了当IDS漏报率γ=10%时IDS检测率α和误报率β对一个易感节点MTTI的影响。从中可看出，当IDS漏报率保持不变的情况下，提高检测率和降低误报率都能增加一个易感节点的MTTI值。但相比较而言，降低误报率比提高检测率更能增加一个易感节点的MTTI值。例如，当α=90%且β值从20%降低到2%时，一个传感节点的MTTI值从约54.2 h增加到约102 h，增加了约88.2%；而当β=10%且α值从80%增加到98%时，一个传感节点的MTTI值从约60 h增加到约73.5 h，增加了约22.5%。由此可见，在IDS漏报率保持不变的情况下，为更有效地提升一个易感节点的可生存性，应采取更多的技术降低IDS的误报率。

图4　当γ=10%时α和β对易感节点MTTI的影响

图5给出了当α=90%时β和γ对一个易感节点MTTI的影响。从中可看出，当IDS检测率保持不变的情况下，降低IDS误报率和漏报率都能增加一个易感节点的MTTI值，但降低IDS误报率更有效。例如，当β=10%且γ值从20%降低到2%时，一个传感节点的MTTI值从约64.5 h增加到约71.25 h，增加了约10.5%；而当γ=10%且 β值从20%降低到2%时，一个传感节点的MTTI值从约54.2 h增加到约102 h，增加了约88.2%。因此，在保持IDS检测率不变的情况下，应尽可能地降低IDS的误报率，从而更有效地提升易感节点的可生存性。

图5　当α=90%时β和γ对易感节点MTTI的影响

图6给出了当β=10%时α和γ对一个易感节点MTTI的影响。从中可以看出，当IDS误报率保持不变的情况下，增加IDS检测率和降低漏报率都能增加一个易感节点的MTTI值，但增加IDS检测率更有效。例如，当α=90%时且γ值从20%降低到2%时，一个传感节点的MTTI值从约64.5 h增加到约71.25 h，增加了约10.5%；而当γ=10%且α值从80%增加到98%时，一个传感节点的MTTI值从约60 h增加到约73.5 h，增加了约22.5%。因此，在保持IDS误报率不变的情况下，应尽可能地增加IDS检测率来提升易感节点的可生存性。

图6　当β=10%时α和γ对易感节点MTTI的影响

4.2整个WSNs的可生存性评估

由式（12），整个WSNs的生存期与恶意程序选择动作Infect的概率 ρI、恶意程序传染成功率λ、一个簇内可选簇头数m、一条路由经过的簇数n、整个WSNs的可选路由数l有关。根据IDS经验参数值，设α=90%，β=10%，γ=10%，通过计算“恶意程序传染博弈”模型的纳什均衡点，可得ρI≈0.148 1，代入式（12），就可讨论WSNs生存期与参数m、n、l值的关系。

图7～图9分别给出了l=3、m=4、n=3时整个WSNs生存期的变化曲线。

图7　当l=3时m和n值对整个WSNs生存期的影响

由图7可以看出，增加一个簇内可选簇头数和减少一条路由经过的簇数都能延长整个WSNs的生存期，但变化趋势不同。例如，当m=4时，随着n值从6减小到5，整个WSNs的生存期从约82.2 h增加到约89.1 h，而随着n值从2减小到1，整个WSNs的生存期从约139.6 h增加到约209.5 h。当n=3时，随着m值从1增加到2，整个WSNs的生存期从约41.3 h增加到约74.1 h，而随着m值从7增加到8，整个WSNs的生存期从约147.6 h增加到约156.1 h。

图8　当m=4时n和l值对整个WSNs生存期的影响

由图8可以看出，减少一条路由经过的簇数和增加整个WSNs的可选路由数能延长整个WSNs的生存期。

图9　当n=3时m和l值对整个WSNs生存期的影响

由图9可以看出，增加一个簇内可选簇头数和整个WSNs的可选路由数都能延长WSNs的生存期。由此可见，根据实际的WSNs生存期需求，利用本文提出的WSNs可生存性方法对设计一个簇应包含的可选簇头数、一条路由应包含的簇数、整个WSNs的可选路由数具有理论指导作用。

5　结论

满足高可生存性是WSNs设计的终极目标。本文为建立高可生存的WSNs提出了一种针对受恶意程序传染的聚簇WSNs可生存性评估方法。建立的“恶意程序传染博弈”模型能预测恶意程序的传染行为，将得到的恶意程序最优传染策略应用于马尔可夫链中的状态转换，从而解决了恶意程序传染的故意性与马尔可夫链的随机性之间的矛盾。提出的评估指标MTTI能反映一个易感节点的可靠度，再根据可靠性理论，得到了能反映一个簇、一条路由、整个WSNs的可靠度和整个WSNs生存期的评估指标。实验结果给出了IDS检测率、误报率和漏报率对提升一个易感节点可生存性的影响，也给出了一个簇中的可选簇头数、一条路由经过的簇数、整个WSNs的可选路由数对整个WSNs生存期的影响，验证了本文方法的有效性，为高可生存的WSNs设计提供了理论基础。

但是，本文提出的可生存性评估方法未考虑WSNs系统的生存恢复能力，而该能力对整个WSNs的可生存性具有重要影响。因此，下一步工作将在考虑WSNs系统生存恢复能力的基础上提出新的WSNs可生存性评估机制。

［1］ 王潮，胡广跃，张焕国.无线传感器网络的轻量级安全体系研究［J］.通信学报，2012，33（2）：30-35.

［2］ Granjal J，Monteiro E，Silva J S.Security in the Integration of Low-Power Wireless Sensor Networks with the Internet：A Survey［J］.Ad Hoc Networks，2015，24（A）：264-287.

［3］ Winkler T，Rinner B.Security and Privacy Protection in Visual Sensor Networks：A Survey［J］.ACM Computing Surveys，2014，47（1）：2，42.

［4］ 周豫苹，黄振杰，王娟，等.一类新的分布式随机验证无线传感网络节点克隆攻击检测［J］.传感技术学报，2014，27（4）：544-550.

［5］ 张惠根，周治平.一种强安全的WSN用户认证及密钥协商方案［J］.传感技术学报，2015，28（8）：1207-1214.

［6］ Wang Y，Wen S，Xiang Y，et al.Modeling the Propagation of Worms in Networks：A Survey［J］.IEEE Communications Surveys and Tutorials，2014，16（2）：942-960.

［7］ 徐恪，朱敏，林闯.互联网体系结构评估模型、机制及方法研究综述［J］.计算机学报，2012，35（10）：1985-2006.

［8］ 王海涛，朱世才，陈晖，等.应急通信中基于ANP的WSN可生存性评价指标体系研究［J］.传感技术学报，2014，27（4）：557-563.

［9］ 朱世才，王海涛，吴连才，等.基于SMP的分簇WSN生存性评估模型［J］.传感技术学报，2014，27（3）：383-387.

［10］熊书明，王良民，詹永照.基于SMP的无线传感器网络拓扑容侵定量评估［J］.通信学报，2010，31（7）：24-32.

［11］袁燎原，章卫国，刘洋，等.混合余度传感器系统的可靠性建模与分析［J］.西北工业大学学报，2015，33（1）：57-62.

［12］刘文芬，张树伟，龚心.一种优化的基于Markov博弈理论的网络风险评估方法［J］.电信科学，2014，30（7）：13-18.

［13］Parvin S，Hussain F K，Park J S，et al.A Survivability Model in Wireless Sensor Networks［J］.Computers&Mathematics with Applications，2012，64（12）：3666-3682.

［14］Petridou S，Basagiannis S，Roumeliotis M.Survivability Analysis Using Probabilistic Model Checking：A Study on Wireless Sensor Networks［J］.IEEE Systems Journal，2013，7（1）：4-12.

［15］Zhang L，Liu T，Guo L，et al.The Survivability Analysis Method of Wireless Sensor Network Based on SPN［J］.Journal of Information and Computational Science，2014，11（6）：1983-1994.

［16］Cai J，Song X，Wang J，et al.Reliability Analysis for a Data Flow in Event-Driven Wireless Sensor Networks［J］.Wireless Personal Communications，2014，78（1）：151-169.

［17］Distefano S.Evaluating Reliability of WSN with Sleep/Wake-Up Interfering Nodes［J］.International Journal of Systems Science，2013，44（10）：1793-1806.

［18］Di Martino C，Cinque M，Cotroneo D.Automated Generation of Performance and Dependability Models for the Assessment of Wireless Sensor Networks［J］.IEEE Transactions on Computers，2012，61（6）：870-884.

［19］Wang Y Q，Yang X Y.Virus Spreading in Wireless Sensor Networks with a Medium Access Control Mechanism［J］.Chinese Physics B，2013，22（4）：040206，5.

［20］李军，刘君华.多传感器融合系统的可靠性模型研究［J］.西安交通大学学报，2004，38（8）：775-778.

［21］Wang X，He Z，Zhang L.A Pulse Immunization Model for Inhibiting Malware Propagation in Mobile Wireless Sensor Networks［J］. Chinese Journal of Electronics，2014，23（4）：810-815.

［22］Mishra B K，Keshri N.Mathematical Model on the Transmission of Worms in Wireless Sensor Network［J］.Applied Mathematical Modelling，2013，37（6）：4103-4111.

［23］Shen S，Li H，Han R，et al.Differential Game-Based Strategies for Preventing Malware Propagation in Wireless Sensor Networks［J］. IEEE Transactions on Information Forensics and Security，2014，9（11）：1962-1973.

［24］Shen S，Han R，Guo L，et al.Survivability Evaluation Towards Attacked WSNs Based on Stochastic Game and Continuous-Time Markov Chain［J］.Applied Soft Computing，2012，12（5）：1467-1476.

［25］Munir A，Antoon J，Gordon-Ross A.Modeling and Analysis of fault Detection and Fault Tolerance in Wireless Sensor Networks［J］.ACM Transactions on Embedded Computing Systems，2015，14（1）：3，43.

沈士根（1974-），男，汉族，绍兴文理学院计算机科学与工程系教授，博士，主要研究方向为无线传感器网络、移动互联网、博弈论，shigens@126.com；

黄龙军（1976-），男，汉族，绍兴文理学院计算机科学与工程系讲师，浙江工业大学计算机科学与技术学院博士生，主要研究方向为电磁纳米网络、无线传感器网络、博弈论，hlj_jlh@163.com；

曹奇英（1960-），男，汉族，东华大学计算机科学与技术学院教授，博士生导师，博士，主要研究方向为普适计算、智能信息处理，caoqiying@dhu.edu.cn。

Survivability Evaluation for WSNs under Malware Infection*

SHEN Shigen1，2*，HUANG Longjun1，3，FAN En1，HU Keli1，LIU Jianhua2，CAO Qiying4
（1.Department of Computer Science and Engineering，Shaoxing University，Shaoxing Zhejiang 312000，China；2.College of Mathematics，Physics and Information Engineering，Jiaxing University，Jiaxing Zhejiang 314001，China；3.College of Computer Science and Technology，Zhejiang University of Technology，Hangzhou 310023，China；4.College of Computer Science and Technology，Donghua University，Shanghai 201620，China）

To ensure dependable transmission of sensed data from sensor nodes in Wireless Sensor Networks（WSNs），we propose a measurement of survivability evaluation for WSNs under malware infection.By introducing a game model that can predict malware behavior，we relate the intent of malware infection to a Markov chain（MC）for describing a successful infection as a MC state transition.We then set up a novel measurement representing the reliability of a susceptible sensor node.After considering clustered WSNs as a parallel-serial-parallel system，we deduce reliability measurements for a cluster，a route，and the entire WSNs.Finally，we attain the measurement to calculate the survival time of the entire WSNs.Experiments show the influence of parameters on the survivability of the entire WSNs，and validate the effectiveness of the proposed method that can build up a theoretical foundation for highly survival WSNs.

wireless sensor networks；survivability evaluation；game theory；malware infection；reliable theory

TP393

A

1004-1699（2016）07-1083-07

项目来源：国家自然科学基金项目（61272034，61572014）

2015-12-30修改日期：2016-02-03