高维纵向属性数据的惩罚广义估计方程分析

尹长明，付聃，田凯

（广西大学数学与信息科学学院，广西南宁530004）

高维纵向属性数据的惩罚广义估计方程分析

尹长明，付聃，田凯

（广西大学数学与信息科学学院，广西南宁530004）

文章证明了分析高维纵向二值属性数据的惩罚广义估计方程估计的渐近存在性，相合性与渐近正态性.

属性数据；惩罚广义估计方程；高维纵向数据；渐近正态性

1　引言和主要结果

二值属性数据在生物学、医学，经济和社会科学等领域中都有广泛的应用.已有大量的文献报道有关连续性的高维纵向数据的研究[1-2]，而研究高维纵向二值属性数据的报道比较少.

设在试验中，对于第i个个体第j次观测，得到响应变量Yij和pn×1维协变量Xij，其中i=1，2，…，n，j=1，2，…，m.设来自不同个体的观测值是相互独立的，来自相同个体则是相关的.令Yij的分布为

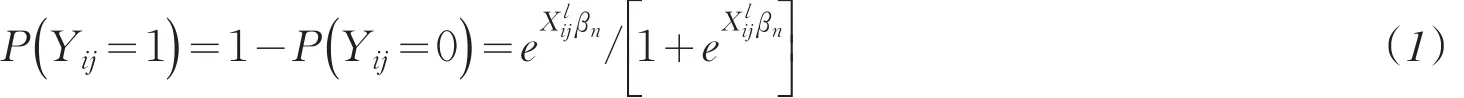
其中βn是未知的回归参数，真值，T表示转置，则易Yij知的期望

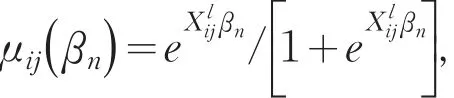
定义惩罚广义估计函数为

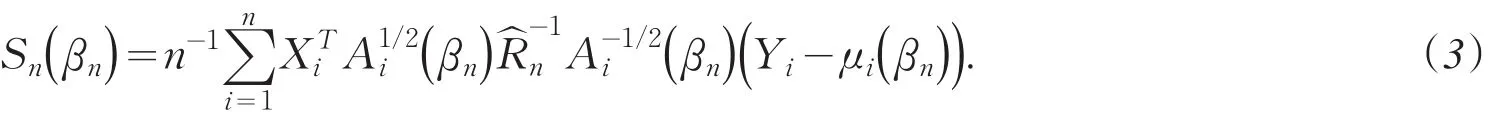
这里

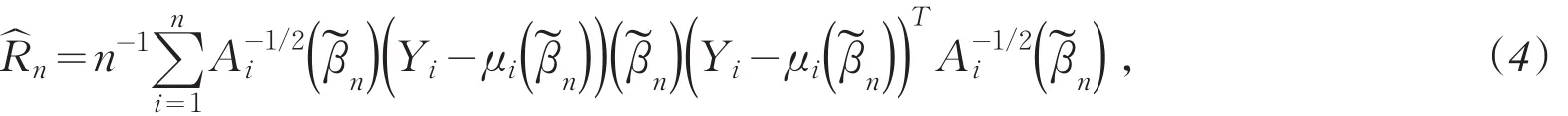
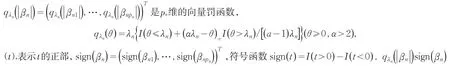
表示它们按分量逐个作出的乘积.

在本文中，C，C1，C2…在不同的位置代表不同的正常数，对矩阵A=（aij），Frobenius范数为

Wang、Zhou和Qu[3]用惩罚广义估计方程研究了高维纵向数据，在较复杂条件得到了估计的渐近性质.本文简化了条件，得到了如下结果：

定理假设以下条件成立：

2　定理的证明

下面证明（7）式.

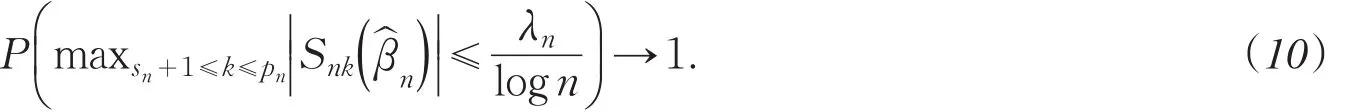
通过证以下两式来证明（10）式：

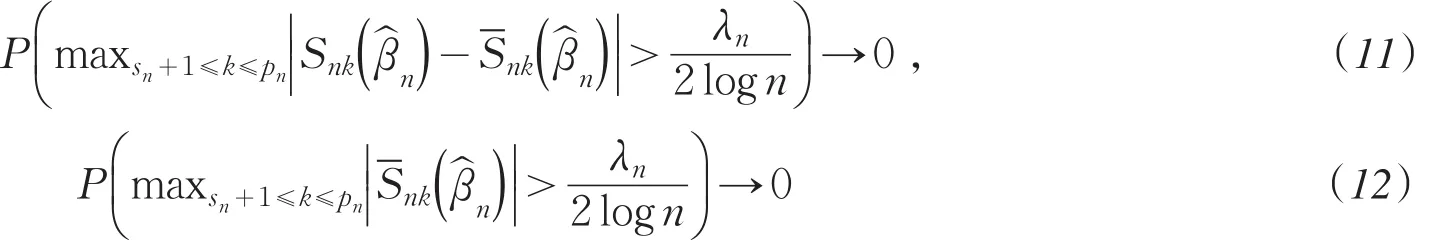
由假定（A1），（A3），（A5）和（A6）可知Wang[4]中的（3.4）式成立，即

由假定（A1），（A5），（A6），（13）式和Markov不等式，可得（11）式左边小于

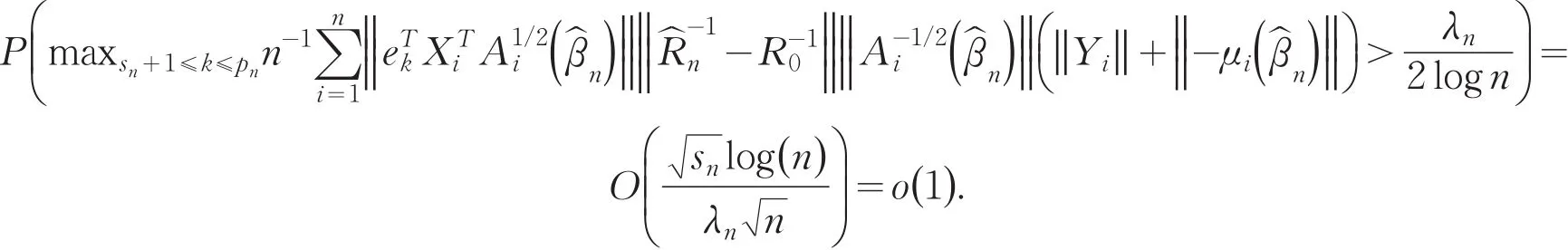
因而（11）式成立.

下面先证（12）式.由Taylor展开式得

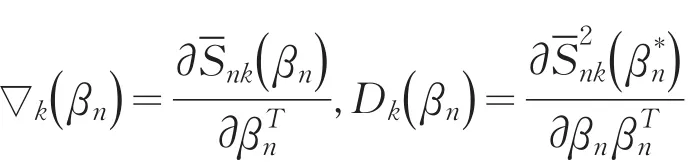
由Berstein’s inequality[5]得

其中，Hnk1=(Hnk1,…,Hnksn)T表示的是由Hnk的前sn个元素组成的子向量，Enk1,Gnk1的定义类似.为了证In21，注意到：

同理可以证得In22=o(1)，In23=o(1)从而In2=o(1).

最后，我们证In3=o(1)，由假定（A1），（A4），（A5），（A6）和（16）式，可得

3　结论

本文是在比文献[3]弱的条件下证明了高维纵向二值属性数据的惩罚广义估计方程估计的存在性，相合性与渐近正态性.虽然在应用上这些条件可以满足，但在理论上显得不够完美，比如条件A1、A3比不带惩罚广义估计方程强，有待理论上进一步研究.

[1]Mc Cullngh P,Nelder J A.Generalized Linear Models[R].London:Chapman and Hall,1983.

[2]Xu P,Wu P,Wang Y,et al.A GEE based shrinkage estimation for the generalized linear model in longitudinal data analysis[R]. Hong Kong:Hong Kong Baptist University,2010.

[3]Wang L,Zhou J,Qu A.Penalized Generalized Estimating Equations for High-Dimensional Longitudinal Data Analysis[J].Bio⁃metrics,2012,68(2):353-360.

[4]Wang L.GEE annalsis of clustered binary data with diverging number of covariates[J].The Annals of Statistics,2011,39(1):389-417.

[5]Bennett G.Probability inequality for sums of independent random variables[J].Journal of the American Statistical Association,1962, 57(297):33-45.

[6]Liang K-Y,Zerger S L.Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73(1):13-22.

责任编辑：刘红

Analysis of Penalized Generalized Estimating Equations for High-Dimensional Longitudinal Attribute Data

YIN Changming，FU Dan，TIAN Kai
（School of Mathematics and Information Science，Guangxi University，Nanning 530004，China）

This paper proves the asymptotic existence,consistency and asymptotic normality of the estimators of the penal⁃ized generalized estimatingequations for the high-dimensional longitudinal two-value attribute data.

attribute data；penalized generalized estimating equations；high-dimensional longitudinal data；asymptotic nor⁃mality

O 212.1

A

1674-4942（2016）01-0006-05

2015-09-17

广西自然科学基金（2015GXNSFAA139006）；国家自然科学基金（11061002）