动态资本注入的最优投资策略

吴杰，黄冬冬，陈传钟

（海南师范大学数学与统计学院，海南海口571158）

动态资本注入的最优投资策略

吴杰，黄冬冬，陈传钟*

（海南师范大学数学与统计学院，海南海口571158）

企业在维持原有经营过程中，将资金投资到股票市场.以盈余用作投资资本，进行多阶段动态投资.盈余过程由布朗运动刻画，效用函数刻画企业对风险和收益的态度.在效用函数最大的前提下，得到了各投资时刻的最优投资组合.该研究为企业提供了一种切实有效的投资策略.

动态投资；布朗运动；效用函数；最优投资组合

投资组合是现代金融的一个重要研究方向，投资组合的选择就是把所有的财富分配到各资产，用于分散风险、保证收益.Markowitz的均值方差理论提供了单时期投资组合选择的基本依据.Merton和Markowitz推导出了单时期投资组合选择的解析表达式.早期对投资组合的研究主要局限在静态投资.1968年，Mossion[1]首次提出多阶段投资组合的数学模型，利用动态规划的方法将单时期推广到多时期的投资组合模型，但未能找到解析解的表达方式.此后有许多学者对其进行研究，Li等[2]用嵌入的方法得出了在自融资前提条件下多阶段动态投资的相关结果.在实际运营中，投资者往往会根据实际的情况，增加投资资金，自融资条件则显得有些局限性.对于企业而言，通过原有的经营过程会带来收益，然而企业若想获得更多的收益，则往往需要通过将部分资金用于投资.此过程，便需要将资金投资到市场中去.显然，投资到股票市场是具有一定的风险，在企业的收益与风险之间需要找到一种平衡，找到一种适合企业实际情况的投资组合.基于此，本文主要研究企业在维持原有经营过程中，将基金用于投资到股票市场.为了不影响企业经营过程，考虑这样一种策略：在观察时刻，将超过边界b的盈余用作投资资本，进行多阶段动态投资.其特点是在每个投资时刻都可能有动态变化的新投资资金加入，资金数量由企业原本运营的过程所决定，动态投资组合更贴近现实.此策略一方面保证了企业的正常运营，另一方面为企业带来了收益.

1　模型

本文考虑公司的盈余过程为如下的风险过程刻画，其中μ>0，σ>0

记Ti，i=1，2，…，n为观察时刻，为一族独立且服从均值为λ的指数分布.对 χi求期望有如下表达式，

其中Φ（x）为标准正态分布函数，当b确定时，可通过查询正态分布表或者数值计算去得到相应的值.由标准布朗运动的性质得到的期望有

现考虑这样一种投资策略，在观察时刻Ti，若公司盈余超过边界b，则将全部超额收益作为注入投资资本.假设市场上具有m+1只风险证券，记为证券1，证券2，…，证券，公司可以将资金投资到任何一只风险证券上，且每次交易没有交易费.现记为第j只证券在时刻的收益率，为时刻投资到证券j上的资金，Zi为时刻Ti企业通过所拥有的总的财富，则为时刻投资到证券m+1上的资金.其中各证券在不同时刻收益率的期望均为已知.记，则公司通过多阶段动态投资在时刻所具有的财富为

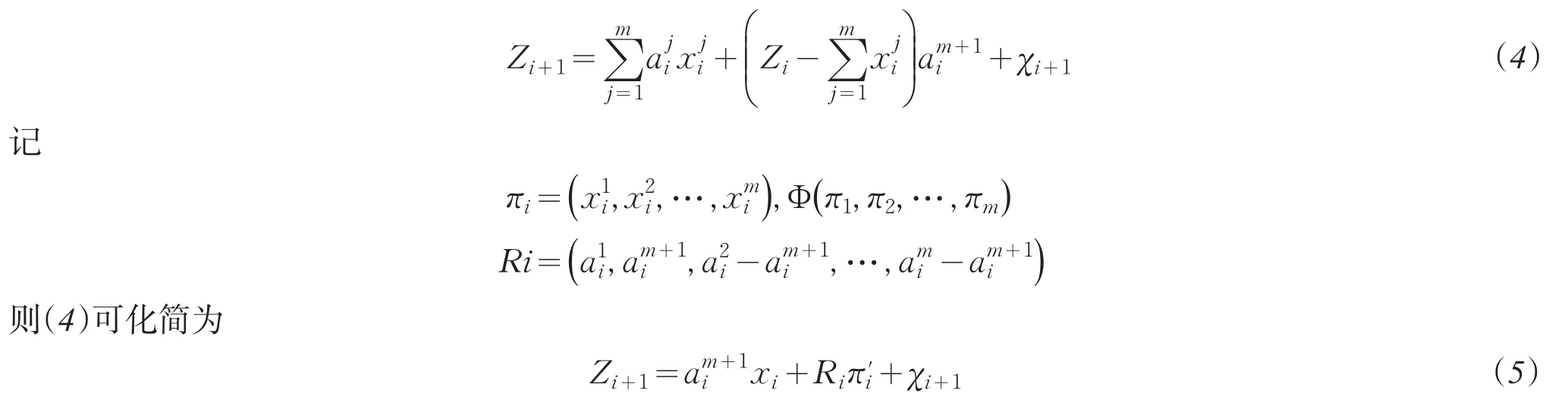
下文中所有均需满足等式（5）.

2　最优投资组合

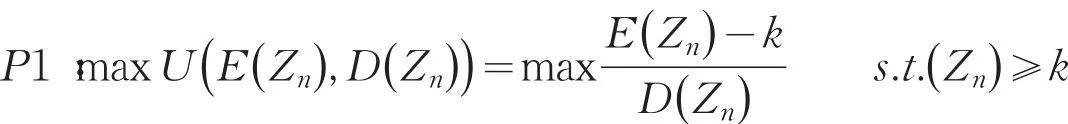
对于问题P1不能直接求解，现引入如下问题

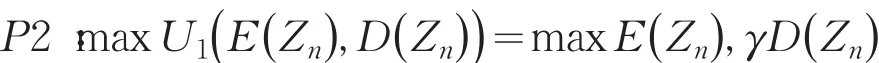
其中γ>0，问题P1和问题P2的等价性由定理1和2说明.记

A1={Φ|Φ为满足P1的投资组合}；A2={Φ|Φ为满足P2的投资组合}

定理1对任意Φ*∈A，存在γ>0使得Φ∈A2.

证明对效用函数U，分别对和求导可得

故效用函数是关于D(Zn)单减和E(Zn)单增的函数，则问题的最优解一定在空间{E(Zn),D(Zn)}中的均值方差有效前沿中，又在空间{E(Zn),D(Zn)}的每一个有效前沿都存在支撑，故每个有效解都可以由问题P2的解生成，定理得证.

证明由效用函数的表达式可知，对于问题P2，其有效解含参数γ，即可由形式表示，由定理1可知A⊆∪λ>0A1，故等价为如下形式

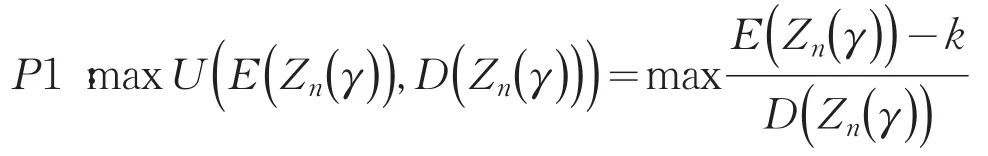
对最优的γ*有

已知Φ*∈A1，则对γ*有

故由定理1和定理2可知，对问题P1的求解可转化为对问题P2的求解.然而对于问题的解也是不能直接求得的，需转化为问题P3的求解，问题P3有如下形式

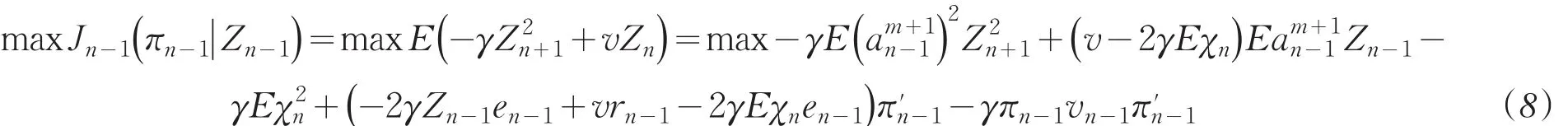
对于最优的投资组合πn-1有

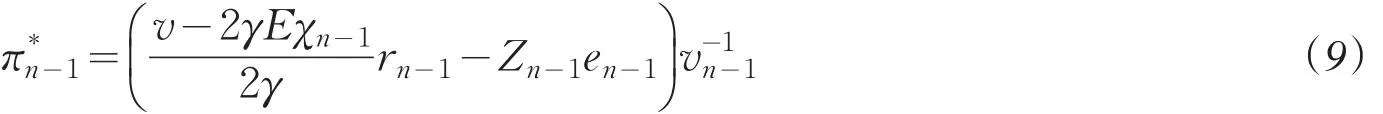
将等式（9）反代回（8）可得

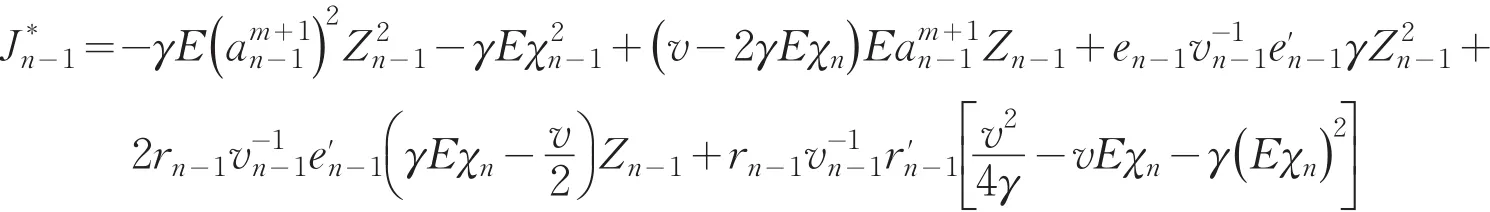
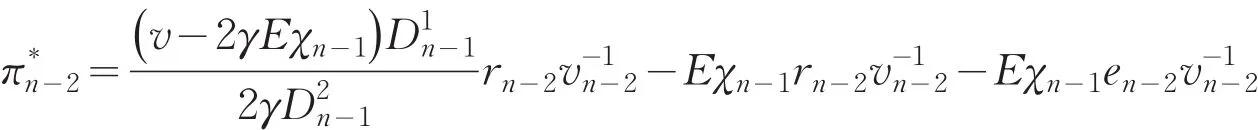
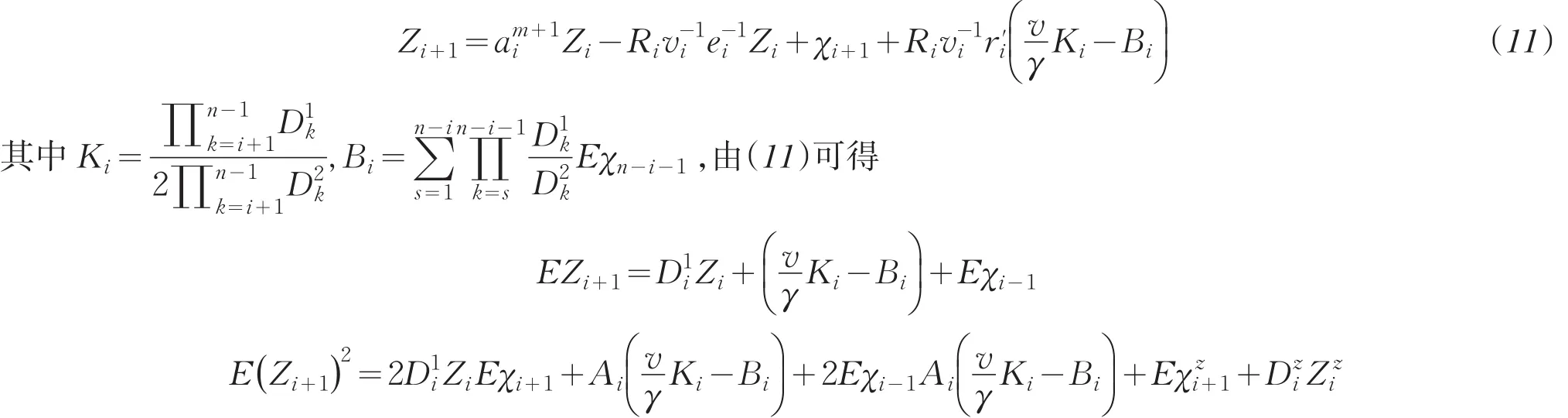
通过迭代得到时刻Tn投资所拥有财富值的期望和财富值平方的期望：

前已述及问题P1和问题P3最优投资组合的关系，也即当问题P3的最优投资组合中的γ和v满足如下等式时，为问题P1的各时间段的最优投资组合.

将所求得的EZn以及E带入上式，得到

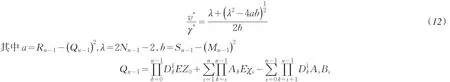
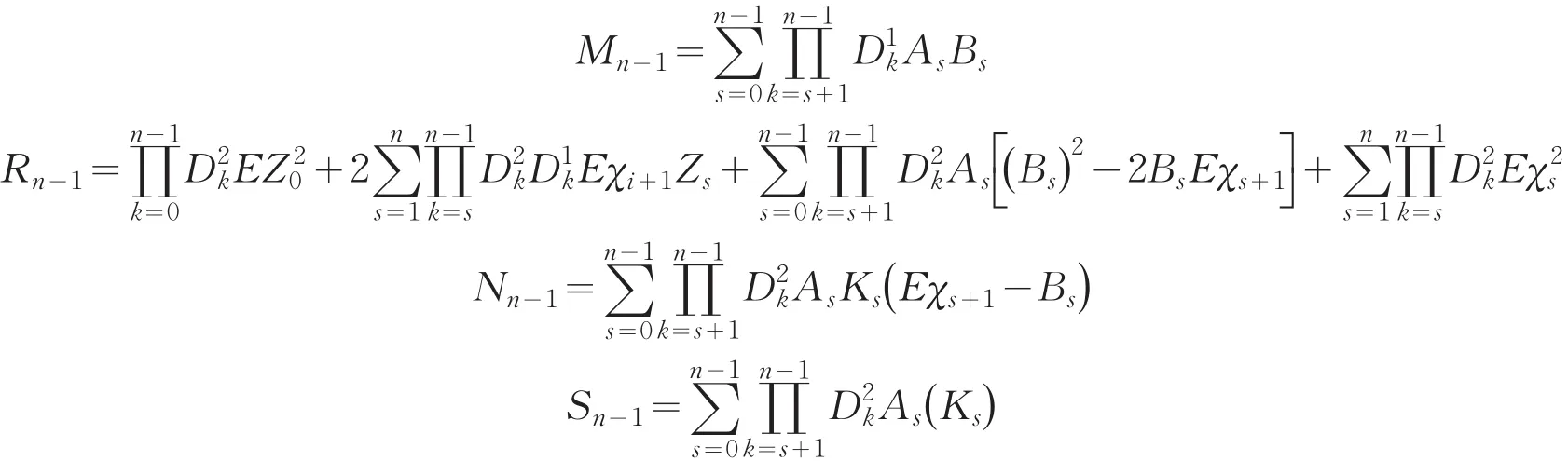
将等式（1）～（3）和等式（12）一并带入等式（10），则得到问题P1在各时刻的投资组合.

3　结论

通过以上证明求解，得到了在满足效用函数U为最大时，企业在各时刻的最优投资组合，平衡了企业对风险的接受能力和对收益的需求.本研究解决了企业在维持正常运营的过程中，如何在自身所能承担风险前提下，去追求更多利益的问题，为企业提供了一种切实有效的投资策略.

[1]Niederinski A,Mossion J.Optimal Multiperiod Portfolio Polices[J].Journal of Business,1968,41:215-229.

[2]Li D.Optimal Dynamic Portfolio Selection:Multiperiod Mean-Variance Formulation[J].Mathematical Finance,2000,10(3):387-406.

[3]Albrecher H,Bauerle N,Thonhauser S.Optimal dividend-payout in random discrete time[J].Stat Risk Model,2011,28(3):251-276.

[4]Hansjrg Albrecher.Randomized observation periods for the compound Poisson risk model Dividends[J].Astin Bull,2011,41(2): 645-672.

[5]Wu H L,Li Z F.Multi-period mean-variance portfolio selection with regime switching and a stochastic cash flow[J].Insurance: Mathematics and Economics,2012,50:371-384.

[6]Li C J,Li Z F.Multi-period portfolio optimization for asset-liability management[J].Appliet Mathematics and Computation, 2012,218:11196-11208.

[7]Wei S Z,Ye Z X.Multi-period optimization portfolio with bankruptcy control in the stochastic market[J].Applied Mathematics and Computation,2006,7(1):1-12.

[8]Albrecher H,Cheung.Randomized observation periods for the compound Poisson risk model dividends[J].Astin Bull,2006,41(2): 645-672.

[9]张鹏,张逸菲.完全市场情况下多阶段均值-VaR投资组合优化[J].武汉科技大学学报,2014,37(4):315-319.

[10]严加安.金融数学引论[M].北京:科学出版社,2012.

[11]刘德彬.投资组合效率评价方法及其应用研究[D].长沙:湖南大学,2015.

责任编辑：刘红

The Optimal Investment Strategy with Dynamic Capital

WU Jie，HUANG Dongdong，CHEN Chuanzhong*
（School of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

Enterprises in maintaining normal operation invest into the stock market.The surpluses are used as investment capital by multi-stage dynamic investment.The surplus process of the enterprise is depicted by a Brownian motion and the attitude towards risk is depicted by utility function.The optimal investment portfolio at each investment time is obtained un⁃der the premise that the given utility function is maximum.The research provides a practical and effective investment strate⁃gy for enterprises.

dynamic investment；Brownian motion；utility function；optimal investment portfolio

O 224

A

1674-4942（2016）01-0017-05

2015-11-21

海南师范大学研究生创新项目（Hsyx2015-39）