基于Karnopp摩擦的柔性滑移铰的建模与仿真†

章杰　王琪

(北京航空航天大学航空科学与工程学院, 北京　100191)



基于Karnopp摩擦的柔性滑移铰的建模与仿真†

章杰†王琪

(北京航空航天大学航空科学与工程学院, 北京100191)

对含Karnopp摩擦的柔性滑移铰系统进行动力学建模和仿真.将滑移铰中的滑块视为柔性体,滑道视为刚性接触面,考虑滑道与滑块之间的间隙.由于柔性滑块与滑道的接触状态和摩擦情况比较复杂,采用有限元方法建立了柔性滑块的力学模型,基于罚函数方法建立含Karnopp摩擦柔性滑移铰接触力模型,通过试算迭代法判断柔性滑块各节点的接触状态,基于KED方法和Newmark方法给出了含该滑移铰机械系统动力学方程的数值算法.最后,以含Karnopp摩擦的柔性滑移铰和驱动摆杆构成的机械系统为例进行动力学仿真,分析了其动力学特性,验证了本文给出的方法的有效性.

柔性滑移铰,Karnopp摩擦,间隙,有限元

引言

滑移铰在机械系统中被广泛应用,但滑移铰中双边约束、摩擦等非线性因素的存在使得相关动力学问题的求解变得复杂,以往的研究常将滑移铰简化为理想铰,即不考虑滑块与滑道之间的摩擦、间隙、碰撞等因素,但这些因素在实际的含滑移铰机械系统中广泛存在[1].近年来不少关于滑移铰动力学行为的研究开始考虑其间隙、摩擦和碰撞等因素对系统动力学行为的影响.文献[1-2]考虑滑块与滑道之间的间隙,用非光滑动力学方法对含滑移铰的平面多刚体系统进行了建模仿真.文献[3]考虑碰撞和摩擦,用线性互补方法对含滑移铰和转铰的机械系统进行了研究.文献[4]考察了间隙、摩擦和碰撞等因素对曲柄滑块机构动力学行为的影响.文献[5-6]考虑摩擦,将间隙视为无穷小且忽略块滑与滑道的碰撞,对含滑移铰的单自由度系统动力学解的存在性和唯一性进行了研究.文献[7-8]同样忽略滑移铰的间隙和碰撞,基于线性互补方法对含库仑干摩擦滑移铰的多体系统动力学行为进行了研究.文献[9-11]对平面和空间含摩擦滑移铰的动力学行为进行了研究.这些研究将滑移铰视为刚体,忽略了滑块变形对系统动力学的影响,如果使用修正的库仑摩擦模型时,无法反映粘滞状态；如果使用库仑干摩擦时,可反映粘滞状态,但是滑块处于粘滞状态时,由于滑道的约束和静摩擦力的存在使得系统处于超静定状态,基于刚体模型已无法唯一地求滑道作用于滑块上的接触力.

文献[12-13]考虑物体接触点的局部变形,基于接触力学理论和线性互补问题的算法, 给出了含接触、碰撞以及库伦干摩擦, 同时具有理想定常约束和非定常约束的平面多刚体系统动力学的建模与数值计算方法,但该方法不适用用于含双边约束的滑移铰系统.

含驱动约束与摩擦的滑移铰在很多机械系统中存在.文献[14]将滑移铰视为柔性体,加入变形协调条件,应用有限元方法系统地研究了间隙、库仑摩擦和滑块变形对曲柄滑块机构动力学行为的影响,但未考虑驱动约束.文献[15-16]对含驱动约束与刚性滑移铰多体系统动力学问题进行了建模和仿真,但该方法无法完全求出处于粘滞状态时接触点的约束力.

本文在上述研究的基础上,研究了基于Karnopp摩擦模型[17]的含间隙柔性滑移铰的建模和数值算法.利用有限元方法和罚函数方法,建立柔性滑移铰的力学模型,应用结构动力学方法建立滑移铰的动力学方程,基于KED方法和Newmark方法给出了含该滑移铰机械系统动力学方程的数值算法,最后通过数值仿真分析含驱动约束和柔性滑移铰机械系统的动力学行为,验证该方法的有效性.

1　含驱动约束与摩擦的柔性滑移铰的建模

1.1滑移铰的接触形式

设滑移铰由滑块和滑道构成,且存在有间隙,因此滑块在滑道内的接触形式如图1所示.

形式1：单面接触状态,如图1(a) (b)所示；

形式2：双面接触状态,如图1(c) (d)所示；

形式3：非接触状态,如图1(e)所示.

图1　滑移铰的接触形式示意图Fig. 1　Contact states oftranslational joint

1.2Karnopp摩擦模型

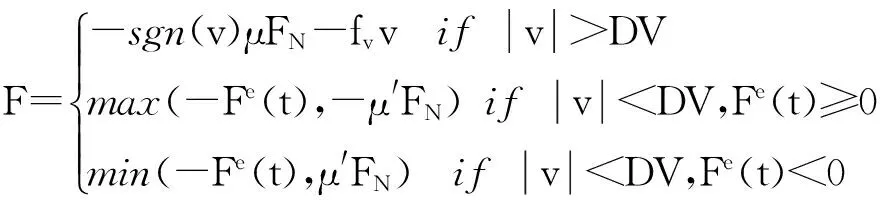
(1)

其中,F是滑道作用于滑块上某一接触面的摩擦力,FN为该接触面的法向力,μ′为静摩擦系数,μ为动摩擦系数,v为滑块质心速度,Fe(t)为作用于滑块上的所有外力(不含滑道与滑块间的作用力)在滑道切向投影的代数和,fvv为粘性摩擦部分,fv为粘性系数,sgn(x)是符号函数

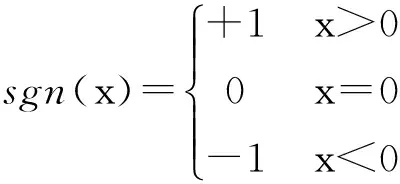
1.3含Karnopp摩擦的柔性滑移铰的接触模型

Karnopp摩擦模型中的摩擦力包括干摩擦部分和粘性摩擦部分,首先对干摩擦部分进行建模.

罚函数方法是解决接触问题应用最广泛的方法之一[14,20],其物理意义是将接触面上各节点处的接触力用线弹性模型描述[14,21-23].本文基于罚函数方法,建立含Karnopp摩擦的柔性滑移铰的接触模型.

应用有限元方法将滑块划分为若干个微小单元,基于文献[14]中接触力和摩擦力的表示方法,将滑块接触面上第i个节点处接触力表述如下：

(2)

其中：Ffi为该节点切向摩擦力,FNi为节点法向接触力,其正方向与图1中坐标系正方向一致.kT和kN分别为切向和法向弹簧的弹簧刚度(罚函数方法中称为罚因子).dTi和dNi分别为该节点在该时刻的微小变形位移在切向和法向上的投影.SurfaceAB和CD分别为滑块的两个接触面,分别由Area1、2和Area3、4构成,如图1所示.ci为接触状态系数,定义为

(3)

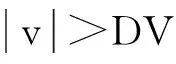
(4)

其中vcτ为滑块质心速度在切向上的投影.

式(2)、(3)和(4)建立了节点接触力和节点微小变形位移之间的函数关系,该节点摩擦力所处状态和接触状态系数ci的判断可由文献[14]给出的方法确定.

由于Karnopp摩擦模型中包含干摩擦项,因此滑块在滑道内的运动将会出现黏滞-滑移(stick-slip)现象,图2,3为基于罚函数方法和干摩擦的性质建立的柔性滑移铰接触模型示意图[14],分别描述了滑块处于双面接触时的stick状态和slip状态.图中用线性弹簧表示了节点接触力和该时刻节点微小位移之间的线性关系,实线表示该节点与滑道接触,虚线表示该节点未与滑道接触,细方框表示该节点处切向摩擦力与法向接触力成正比例关系.

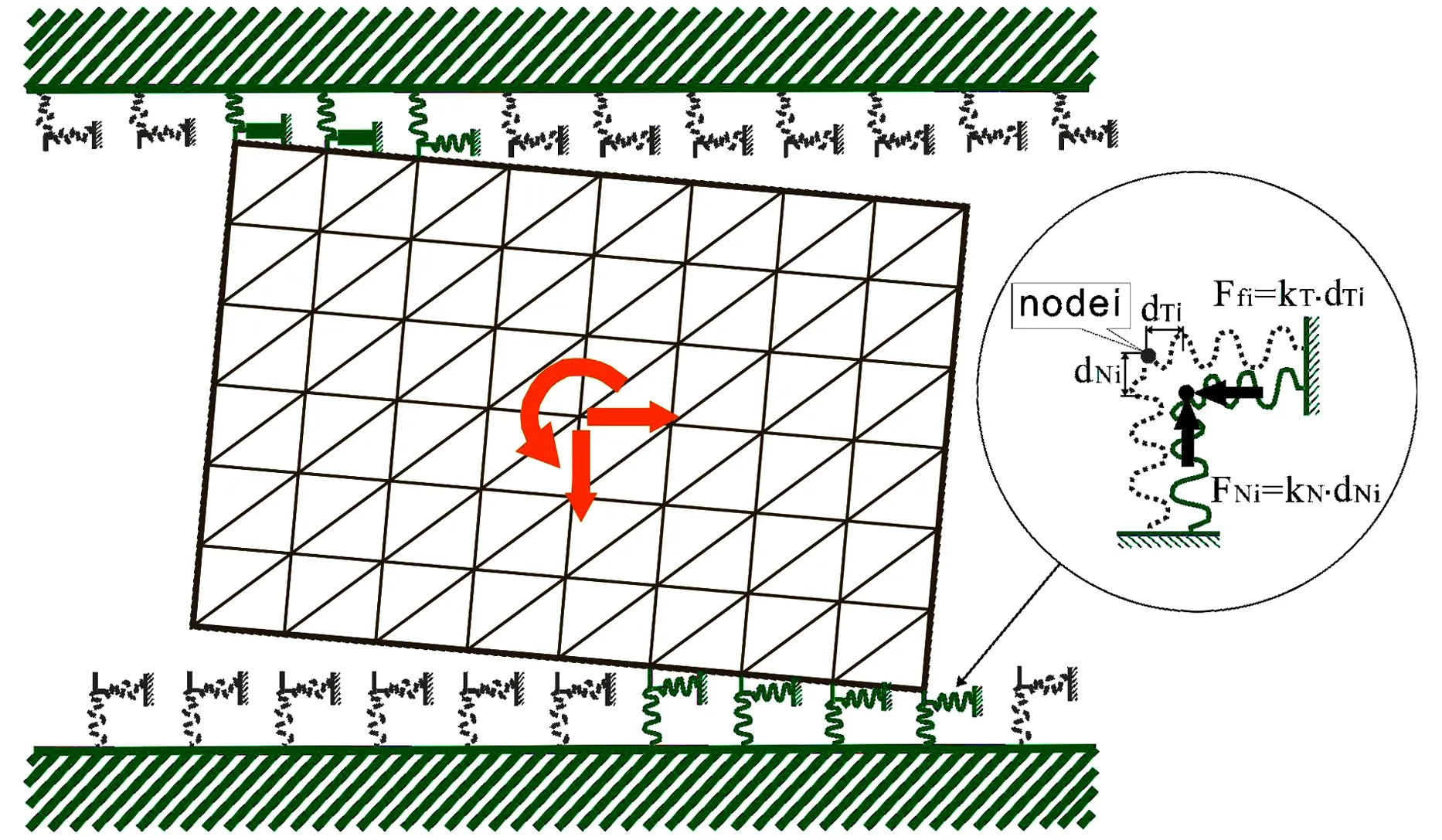
图2　Stick状态下滑移铰接触模型Fig. 2　Model of the interaction of slider under stick state

图3　Slip状态下滑移铰接触模型Fig. 3　Model of the interaction of slider under slip state

2　滑移铰系统动力学方程及其求解策略

Fc=Kcd

(5)

其中,Kc为滑移铰接触刚度矩阵.基于含柔性滑移铰多体系统动力学的试算迭代方法[14],并根据接触状态和运动状态,由(2)-(4)计算可得到该矩阵.

考虑Karnopp摩擦模型中的粘性项fv=-kvv, 应用有限元中的动力学方法[23],含Karnopp摩擦的柔性滑块动力学方程为

(6)

应用牛顿欧拉法建立处滑移铰外其它刚体的动力学方程,方程的一般形式如下：

(7)

3　算例

设含柔性滑移铰的机械系统如图4所示,摆杆AB铰接于滑块B并由电机驱动以角速度ω0转动.滑道与滑块间的摩擦为Karnopp摩擦,用本文给出的方法对其进行动力学仿真.

在如图4所示系统中,均质滑块长为a,高为b,质量为m2,水平弹簧的刚度系数为k,外激励F=F0sin(Ωt)作用于滑块质心.滑块和滑道之间的动摩擦系数和静摩擦系数分别为μ和μ′.摆杆AB质量为m1,长度为L,摆杆质心C坐标为x1,y1,滑块质心B的坐标为x2,y2.柔性滑块的弹性模量为E,泊松比为v,滑块被划分为684个平面三节点三角形单元.相关的参数设定如下：

m1=2.0kg, m2=1.0kg, a=0.6m, b=0.5m,

F0=3.0N, ω0=π/4s-1, k=1.0, L0=0.25m,

Ω=π/2s-1, μ=0.03,μ′=0.04, L=2.0m,

E=2.1×1011pa, v=0.25

系统初始条件为：

x1=1.0m, y1=0.0m, θ1=0.0rad

x2=0.0m, y2=0.0m

图4　滑移铰摆杆机构示意图Fig. 4　Slider-bar system with driving constraint

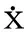
图5　滑块质心坐标x2的时间历程图Fig. 5　Time history of coordinate x2for slider mass center

图6　滑块质心速度2的时间历程图Fig. 6　Time history of velocity 2for slider mass center

图7　滑块质心加速度2的时间历程图Fig. 7　Time history of acceleration 2for slider mass center

图8为驱动力矩的时间历程图,可以看到在某几个时刻会发生微小突变.该突变是由于摩擦力的突变引起滑移铰加速度的突变导致驱动力矩的突变.

图8　驱动力矩的时间历程图Fig. 8　Time history of driving moment

图9给出了柔性滑移铰四个区域摩擦力的时间历程图,其中摩擦力在某段时间区间内恒为零,则表明该区域处于未接触状态.

图9　不同区域摩擦力的时间历程图Fig. 9　Time history of the nodal friction forces at different areas

4　结论

本文提出了含Karnopp摩擦的柔性滑移铰系统的建模与仿真方法,研究了Karnopp摩擦、滑块变形、驱动约束和间隙对滑移铰动力学行为的影响.基于有限元方法和罚函数方法,建立含Karnopp摩擦的柔性滑移铰的接触模型并建立其动力学方程,用试算迭代法确定柔性滑块各节点的接触状态系数并计算各节点摩擦力,基于KED方法和Newmark方法对含Karnopp摩擦的柔性滑移铰和驱动摆杆构成的机械系统进行了数值仿真.仿真结果表明了该方法的有效性,并揭示了滑块的摩擦与变形,以及驱动摆杆对滑移铰动力学行为的影响.与基于滑块刚体模型的方法相比,该方法不但能计算滑块变形对该滑移铰动力学行为的影响,也能求解该滑块处于双面接触且处于stick状态时的接触力.

1FloresP,LeineR,GlockerC.Modelingandanalysisofplanarrigidmultibodysystemswithtranslationalclearancejointsbasedonthenon-smoothdynamicsapproach. Multibody System Dynamics, 2010,23(2):165～190

2FloresP,AmbrósioJ,ClaroJCP,LankaraniHM.Translationaljointswithclearanceinrigidmultibodysystems. Journal of Computational and Nonlinear Dynamics, 2008,3(1):112～113

3ThümmelT,FunkK.Multibodymodellingoflinkagemechanismsincludingfriction,clearanceandimpact.In:ProceedingsofTenthWorldCongressontheTheoryofMachineandMechanisms,OuluUniversity,Finland, 1999,4:1375～1386

4FarahanchiF,ShawS.Chaoticandperiodicdynamicsofaslider-crankmechanismwithsliderCclearance. Journal of Sound and Vibration, 1994,177(3): 307～324

5KleppHJ.Theexistenceanduniquenessofsolutionsforasingle-degree-of-freedomsystemwithtwofriction-affectedslidingjoints. Journal of Sound and Vibration, 1995,185(2):364～371

6KleppHJ.Modesofcontactanduniquenessofsolutionsforsystemswithfriction-affectedsliders. Journal of Sound and Vibration, 2002,254(5):987～996

7ZhuangFF,WangQ.Modelingandsimulationofthenonsmoothplanarrigidmultibodysystemswithfrictionaltranslationaljoints. Multibody System Dynamics, 2013,29(4):403～423

8WangQ,PengHL,ZhuangFF.Aconstraint-stabilizedmethodformultibodydynamicswithfrictionaffectedtranslationaljointsbasedonHLCP. Discrete and Continuous Dynamical Systems-Series B, 2011,2(2):589～605

9罗晓明,齐朝晖,孔宪超. 平面棱柱铰内考虑摩擦效应的接触分析. 计算力学学报,2012,29(3):387～392 (LuoXM,QiZH,KongXC.Non-collidingcontactanalysiswithfrictionintheplanarprismaticjoint. Chinese Journal of Computational Mechanics, 2012,29(3):387～392 (inChinese))

10QiZH,LuoXM,HuangZH.Frictionalcontactanalysisofspatialprismaticjointsinmultibodysystems. Multibody System Dynamics, 2011,26(4):441～468

11QiZH,XuYS,LuoXM,YaoSJ.Recursiveformulationsformultibodysystemswithfrictionaljointsbasedontheinteractionbetweenbodies. Multibody System Dynamics, 2010,24(2):133～166

12王晓军,王琪. 含摩擦与碰撞平面多刚体系统动力学线性互补算法. 力学学报,2015,47(5):814～821(WangXJ,WangQ.Alcpmethodforthedynamicsofplanarmultibodysystemswithimpactandfriction. Chinese Journal of Theoretical and Applied Mechanics, 2015,47(5):814～821 (inChinese))

13王晓军,王琪. 含非对称摩擦平面运动刚体动力学LCP方法. 北航学报,2015,41(11):2023～2028 (WangXJ,WangQ.Alcpmethodfordynamicsofplanar-motionrigid-bodywithnon-symmetricfriction. Journal of Beijing University of Aeronautics and Astronautics, 2015,41(11):2023～2028 (inChinese))

14ZhangJ,WangQ.Modelingandsimulationofafrictionaltranslationaljointwithaflexiblesliderandclearance. Multibody System Dynamics, 2015: 1～23

15ZhuangFF,WangQ.Modelingandanalysisofrigidmultibodysystemswithdrivingconstraintsandfrictionaltranslationjoints. Acta Mechanica Sinica, 2014,30(3):437～446

16王晓军,王琪,庄方方. 含摩擦滑移铰及驱动约束多刚体系统数值算法. 动力学与控制学报,2014,12(4):336～340 (WangXJ,WangQ,ZhuangFF.Thenumericalmethodformultibodysystemwithfrictionaltranslationaljointsanddrivingconstraints. Journal of Dynamics and Control, 2014,12(4):336～340 (inChinese))

17刘丽兰,刘宏昭,吴子英,王忠民. 机械系统中摩擦模型的研究进展. 力学进展,2008,38(2):201～213 (LiuLL,LiuHZ,WuZY,WangZM.Anoverviewoffrictionmodelsinmechanicalsystems. Advances in Mechanics, 2008,38(2):201～213 (inChinese))

18王琪,庄方方,郭易圆,章杰,房杰. 非光滑多体系统动力学数值算法的研究进展. 力学进展,2013,43(1):101～111 (WangQ,ZhuangFF,GuoYY,ZhangJ,FangJ.Advancesintheresearchonthenumericalmethodfornon-smoothdynamicsofmultibodysystems. Advances in Mechanics,2013,43(1):101～111 (inChinese))

19KarnoppD.Computersimulationofstickslipfrictioninmechanicaldynamicsystems. ASME Journat of Dynamic systems, Measurement and Control, 1985,107(1):100～403

20IurianC.Identificationofasystemwithdryfriction[PhDThesis].Catalunya:UniversityPolitenicadeCatalunya, 2005:45～49

21MachadoM,MoreiraP,FloresP,etal.Compliantcontactforcemodelsinmultibodydynamics:evolutionoftheHertzcontacttheory. Mechanism and Machine Theory,2012,53(7):99～121

22WasfyTM.Asperityspringfrictionmodelwithapplicationtobelt-drives.In:ProceedingsofASME2003InternationalDesignEngineeringTechnicalConferencesandComputersandInformationinEngineeringConference,September2-6,Chicago,USA, 2003:371～378

23王勖成. 有限单元法.北京:清华大学出版社, 2003(WangXC.Finiteelementmethod.Beijing:TsinghuaUniversityPress, 2003 (inChinese))

*TheprojectwassupportedbytheNationalNaturalScienceFoundationofChina(11372018)

†CorrespondingauthorE-mail:jiezhanghunan@126.com

10January2016,revised24February2016.

MODELINGANDANALYSISOFFLEXIBLETRANSLATIONJOINTWITHKARNOPPFRICTION†

ZhangJie†WangQi

(School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing100191, China)

AdynamicmodelofflexibletranslationaljointwithKarnoppfrictionispresentedinthispaper.Theslideroftranslationaljointistreatedasflexiblebody,whiletheguidesaretreatedasrigid.Meanwhile,theinfluencesofclearanceonthedynamicsofsystemsareconsidered.Sincethefrictionforcesandcontactstatesbetweenthesliderandguidesarecomplicated,amechanicalmodelisproposedusingfiniteelementmethod,whereacontactmodelisdevelopedbasedonPenaltymethodandthetime-varyingcontactstatesofnodesaredeterminedbyapplyingtrial-and-erroralgorithm.BasedonKEDmethodandNewmarkmethod,asimulationmethodisproposedtosolvekineticequationsofthetranslationaljoint.Eventually,aplanarslider-barsystemwithKarnoppfrictionandflexiblesliderissimulated,andthedynamicresponseofthemechanicalsystemisanalyzed.Moreover,thenumericalresultsrevealthereasonabilityofthenewdevelopedmethod.

flexibletranslationaljoint,Karnoppfriction,clearance,finiteelementmodel

E-mail:jiezhanghunan@126.com

10.6052/1672-6553-2016-004

2016-01-10收到第1稿,2016-02-24收到修改稿.

*国家自然科学基金资助项目(11372018)资助项目