基于贝叶斯网络的研究生入学奖学金评定

郝晓平

(上海理工大学 光电信息与计算机工程学院，上海 200093)



基于贝叶斯网络的研究生入学奖学金评定

郝晓平

(上海理工大学 光电信息与计算机工程学院，上海 200093)

研究生入学奖学金评价体系的建立是我国高校研究生培养机制改革中的重要问题。为了公平、公正地对研究生入学奖学金进行评定，需要把握影响奖学金等级评定的相关因素，并分析这些因素之间的内在关系。文中以历史数据为依据采用K2算法构建评定奖学金等级的贝叶斯网络模型，并基于概率推理算法对奖学金的等级进行预测。研究结果表明，该方法是可行的，其准确率高达88%，为研究生入学奖学金的评定提供了科学依据。

奖学金等级；评定；K2算法；贝叶斯网络

研究生全面收费带来了研究生教育管理模式的转变，同时对研究生奖学金的评定提出了更高的要求。目前，国内众多学者已对奖学金的评定开展了研究工作。文献[1]从研究生管理的角度出发，依据AHP的原理选择评定指标体系，构建研究生奖学金的评定模型。文献[2]结合数学模型建立了基于多层次综合定量的奖学金评价体系。文献[3]提出了基于Q值法的先席位后金额奖学金自动分配方案，并取得了良好的应用效果。文献[4]利用决策树方法，对奖学金数据进行数据挖掘，构建了一种科学合理的奖学金评价体系。这些研究表明如何正确评定奖学金，是研究生教育的一项重要内容。

贝叶斯网络(BayesianNetwork，BN)是基于概率论和图论的不确定知识表示和推理模型[5]，采用有向无环图来表示变量之间独立性的关系，通过计算概率值来预测和推断不确定的事件。研究生奖学金的评定需要有效地表示各影响因素之间的相互关系，进而有效地描述并推演其中蕴含的不确定性，即需要构建有效的不确定性知识框架、并进行概率的推理计算。因此，可将贝叶斯网络方法运用于研究生奖学金评定的研究。

以上海理工大学研究生招生的历史数据为根据，构建影响奖学金评定的各因素之间相互关系的贝叶斯网络，包括有向无环图(DirectedAcyclicGraph，DAG)构建和条件概率表(ConditionalProbabilityTable，CPT)学习，然后基于概率推理算法来推断研究生入学奖学金的等级。

1　贝叶斯网络

1.1贝叶斯公式

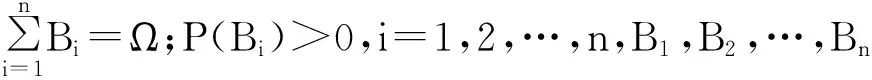
(1)

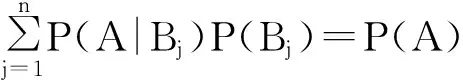
1.2链式法则

贝叶斯网络一般是指带有概率信息的有向无环图。图的每个顶点代表随机变量，边代表变量之间的概率关系。假设y1,y2,…,yn是一贝叶斯网络图中的节点，如果节点yi与yj之间有依赖关系，则必有一条有向弧连接两个节点[6]。在贝叶斯网络中，每个节点在给定其父母节点后条件独立于它的前辈节点，故有

(2)

图1　贝叶斯网络图

如图1所示，设有6个变量y1,y2,y3,y4,y5,y6，全部的概率分布则被分解为各个相关的部分。根据链式法则，联合概率P(y1,y2,y3,y4,y5,y6)可基于各变量的条件概率组成

P(y1,y2,y3,y4,y5,y6)=

P(y1),P(y2),P(y3|y1),P(y4|y1,y2),

P(y5|y4),P(y6|y4)

(3)

1.3贝叶斯网络学习

贝叶斯网络的学习包括结构学习和参数学习，其中结构学习是贝叶斯网络研究中的热点和难点，并被证明是NP-Hard问题。因此在实际计算中，并不是对所有的结构分别计算其评分值，再进行比较取最优，而是采用搜索算法，如K2算法[7]、爬山算法、禁忌搜索、模拟退火等。这些算法按照某种评分函数在可能的拓扑结构空间中进行搜索，通过最高的评分来获取一个最优网络结构。最常用的评分函数有基于贝叶斯统计BDe(BayesianDirichlet-LikelihoodEquivalence)[8]、最小描述长度MDL(MinimumDescriptionLength)和贝叶斯信息标准BIC(BayesianInformationCriterion)。

一个完整的贝叶斯网络除了具有网络结构外，还包括网络参数，即条件概率表[9]。贝叶斯网参数学习[9-10]一般可以分为似然估计方法和贝叶斯估计方法两大类。似然估计方法是最简单的方法，通过对样本数据进行简单的统计得出需要的概率值，如果网络结构和样本数据已知，那么可以从样本数据中进行统计得出相应概率[11]。根据贝叶斯公式可知，以X2和X3为父亲结点集，X1的条件概率参数可由式(4)计算。

P(X1=x1|X2=x2,X3=x3)=

(4)

2　贝叶斯网络模型

2.1影响入学奖学金评定的主要因素

①将所有与运维相关的活动纳入一个统一、规范、透明、前台化的管理轨道，有效克服传统管理方式带来的运维活动后台性强、信息分散、过于依赖个体等弊端。

根据2014年上海理工大学硕士研究生复试办法，研究生入学奖学金的评定依据学生的录取成绩，录取成绩为初试成绩与复试成绩的加权计算和，即

录取成绩=(初始成绩÷5)×55%+复试成绩×45%

(5)

学校以优先录取第一志愿考生为原则，分别对第一志愿和调剂考生的录取成绩进行由高分到低分的排序，并以此确定录取名单，进而评定奖学金等级。学校按照一定的比例和标准，将奖学金设置为3个等级，如表1所示。

表1　2014级研究生学业奖学金资助标准

2.2奖学金等级评定模型的构造

全国硕士研究生报考自2005年开始采用全国统一网上报名的方式，教育部网上报名系统为各招生单位提供了考生超过60条的属性信息，包含姓名、生源地、毕业院校、学历、考生来源等信息。表2为从上海理工大学2014年的历史数据(450行)中选取的与研究生入学奖学金评定相关的代表属性。各变量均为离散型变量，例如，“是否毕业于985/211院校”的取值可确定为1和2，分别表示“985/211院校”和“其他院校”；“考生类别”取值为1、2和3，分别表示“应届生”、“往届生”和“保送生”等。

贝叶斯网络建模一般有3种方法：依靠专家建模、从数据中学习、从知识库中创建。本文采用K2算法从数据中学习贝叶斯网络的结构。K2算法定义一种评价网络结构优劣的评分函数如BDe评分函数，从一个网络开始，根据事先确定的最大父节点数目和节点次序，选择分值最高的节点作为该节点的父节点。对于所研究的问题，选取其中2/3作为训练集，1/3作为测试集，限制最大父节点数为2，采用K2算法可得到如图2所示的有向无环图。

表2　研究生入学奖学金评定的代表属性

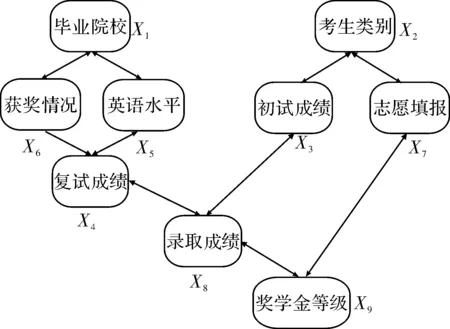
图2　奖学金评定相关因素的贝叶斯网络图

2.3条件概率表的计算

采用似然估计法获得条件概率表。例如X1无父节点，则它的边缘概率为

同时有P(X1=2)=1-P(X1=1)≈0.86。

对于节点X4，其父节点为X5和X6，则条件概率为

P(X4=1|X5=1,X6=1)=

同理可求得P(X4=1|X5=1,X6=2)≈0.42;P(X4=1|X5=2,X6=1)≈0.44;P(X4=1|X5=2,X6=

2)≈0.28。类似可求出其它节点的条件概率，从而得到如图3的条件概率表。

3　基于贝叶斯推理的奖学金等级预测

根据得到的贝叶斯网络结构图和条件概率表，使用测试数据集对其进行测试，例如以预测条件X7=1和X8=1时奖学金各等级的条件概率为例，根据式(1)和式(2)分析奖学金等级预测的过程和结果，为

P(X9=1|X7=1,X8=1)=

同理可求得P(X9=2|X7=1,X8=1)≈0.14;P(X9=1|X7=1,X8=1)≈0.04。

由计算得出的各条件概率，将奖学金等级预测为一等。对测试集所有样本测试后，得到结果如表3所示，其准确率达88%。

表3　研究生入学奖学金评定的预测结果

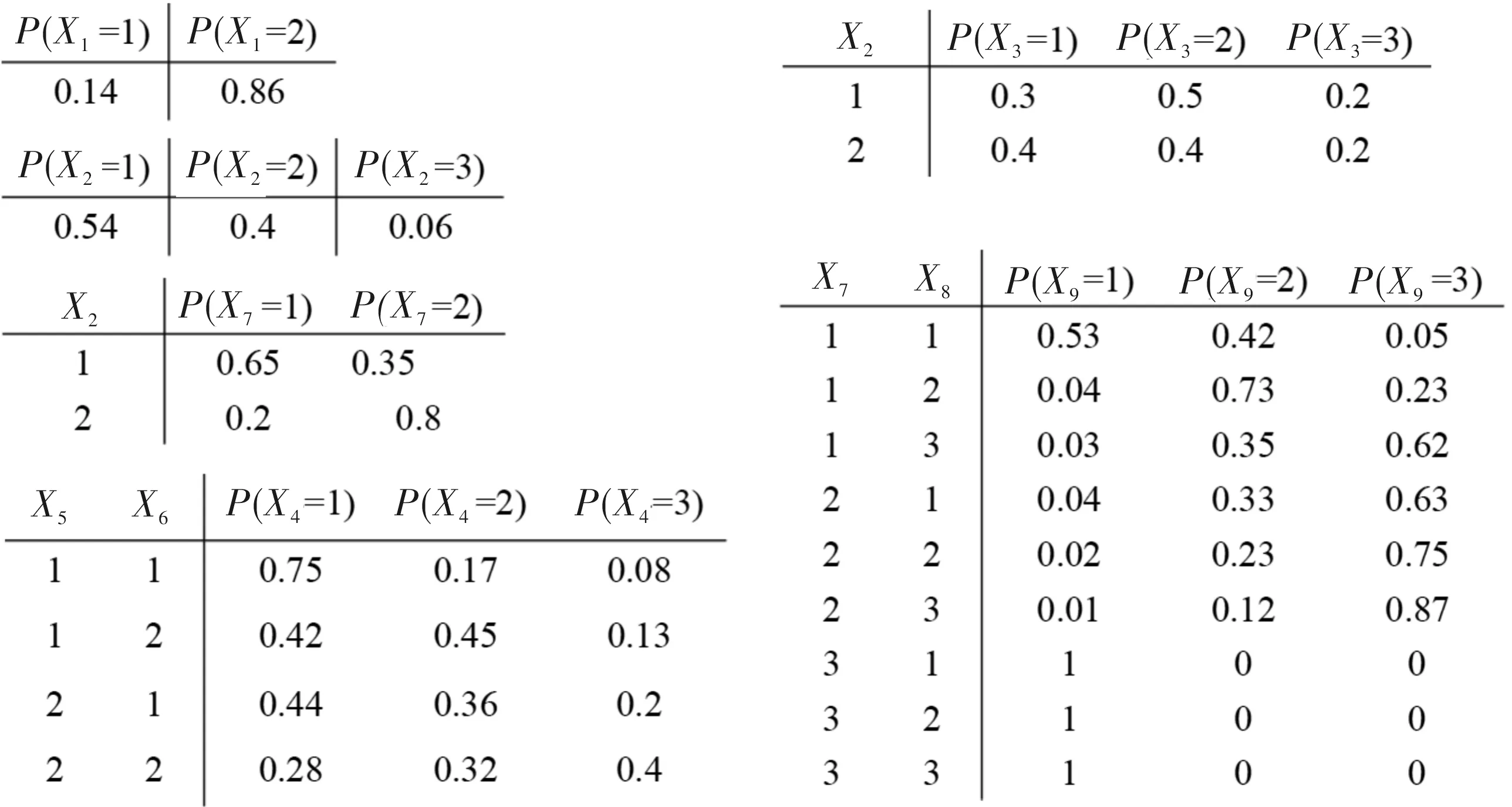
图3　条件概率表

4　结束语

本文就研究生入学奖学金评定的问题构建贝叶斯网络模型，以图形表示方法直观、准确地描述影响研究生入学奖学金评定的各因素之间的相互关系，确定模型参数。基于贝叶斯网络概率推理算法对奖学金等级进行预测，结果表明该网络模型及其构造方法是准确、有效的，为教学管理部门进行科学决策提供了参考。

[1]朱思玮,朱宏.研究生奖学金评定的AHP模型构建[J].廊坊师范学院学报：自然科学版，2014,14(2):22-24.

[2]常方圆,黄海.基于多层次综合定量评价体系的研究生奖学金制度探索[J].兰州教育学院学报,2013,29(2):76-78.

[3]邵正隆,王悫,邹向荣.基于Q值法的奖学金自动分配方案的设计与应用[J].计算机应用,2011,31(11):3132-3134.

[4]卢铮松.研究生奖学金的决策树分类数据挖掘研究[J].计算机工程与应用,2012,48(26):139-143.

[5]Pearl J.Probabilistic reasoning in intelligent systems:networks of plausible inference[M].San Mateo:Morgan Kaufmann Publishers，1988.

[6]Lin Xiaohui,Ma Ping,Li Xiaolan,et al.A learning method of bayesian network structure[C]. Shanghai: IEEE International Conference on Fuzzy Systems & Knowledge Discovery,2012.

[7]Cooper G,Herskovits E.A Bayesian method for theinduction of probabilistic networks from data[J].Machine Learning,1992,9(4):309-347.

[8]Heckerman D,Geiger D,Chickering D.Learningbayesian networks:The combination of knowledge and statistical data[J].Machine Learning,1995,20(9):197-243.

[9]Russel S，Norvig P.Artificial intelligence-A modernapproach[M].Boston: Publishingas Prentice-Hall,2002.

[10]黄建明.贝叶斯网络在学生成绩预测中的应用[J].计算机科学,2012,39(11A):280-282.

[11]徐瑾,岳昆,钱文华,等.一种基于概率图模型的研究生生源质量评价方法[J].云南大学学报：自然科学版,2011,33(S2):299-304.

Research on Scholarship Evaluation for Graduates Admission Based on the Bayesian Network

HAOXiaoping

(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

Theestablishmentofthesystemofgraduatescholarshipsevaluationisoneofthemostimportantproblemsinthegraduateeducationreform.Inordertoassessgraduatescholarshipsmorefairlyandequitably,itisneededtoanalyzetherelevantfactorsofscholarshiplevelsandtheirintrinsicrelationships.Basedonhistoricaldata,aBayesiannetworkmodelforevaluationofscholarshiplevelsisconstructedbyusingtheK2algorithmandtheprobabilisticinferencealgorithmsforprediction.Theresearchresultsshowthattheproposedmethodisfeasibleanditsaccuracyisashighas88%.Thestudypresentsascientificmethodfortheevaluationofgraduateadmissionscholarship,whichprovidesagoodguidanceforthefuturescholarshipevaluation.

scholarshiplevel;evaluation;K2algorithm;Bayesiannetwork

2016- 12- 08

沪江基金资助项目(C14002)

郝晓平(1991-)，女，硕士研究生。研究方向：数据挖掘和机器学习。

10.16180/j.cnki.issn1007-7820.2016.09.010

TP311.12

A

1007-7820(2016)09-034-04