基于随机模型预测控制的欧式期权动态对冲研究

张卫国+杜谦

摘要：应用随机模型预测控制方法研究了欧式期权的动态对冲问题，该方法能够灵活选择适合的目标函数、股票价格预测模型以及显式处理交易费用约束。通过蒙特卡洛仿真对基于随机模型预测控制的对冲方法和delta对冲方法的效果进行了对比分析，并且对华夏上证50ETF期权合约进行了实证检验，检验结果表明了基于随机模型预测控制的对冲方法的有效性。

关键词：随机模型预测控制；动态对冲；交易费用

中图分类号：F831 文献标志码：A 文章编号：1009-055X（2016）04-0001-09

doi：1019366/jcnki1009-055X201604001

引言

经证监会批准，我国首只场内交易的期权产品“华夏上证50ETF期权”于2015年2月9日在上海证券交易所上市交易，开启了中国资本市场期待已久的“期权元年”，丰富了我国资本市场上的金融产品，增加了风险管理的手段。

期权的定价和对冲问题一直是学术界研究的热点，对资本市场上期权、结构化产品的设计和交易有着重大意义。Black和Scholes（BS）及Merton对期权的定价和对冲研究做出了开创性的贡献，他们设定股票价格变动模型为布朗运动的随机扩散模型，通过伊藤引理和积分变换求解随机微分方程得到了欧式看涨和看跌期权的精确价格。[1-2]他们提出的模型称为BSM模型，它假设波动率为常数、无交易费用、连续时间对冲，这与实际市场情况不相符，直接应用BSM模型可能带来较大的对冲误差。对此，学者们在BSM模型的基础上不断对模型加以改进。例如： Merton在BSM模型的基础上加入服从泊松过程的跳跃部分来描述股价的跳跃现象；[3]Heston放松BSM模型中波动率为常量的限制，提出了Heston随机波动模型[4]，他假设波动率服从CIR模型；[5]Bakshi等假设股票价格服从随机利率、随机波动率以及泊松跳跃过程的模型，全面考虑市场上影响期权价格的波动率风险、利率风险、跳跃风险等主要风险，提出了BCC模型，该模型具有更高的自由度，可以根据市场数据来校准模型的参数，通过傅里叶变换得到精确的期权定价公式。[6]

期权对冲最常见的方法为delta对冲，即投资组合中标的股票的投资份额等于期权价格关于标的股票价格的一阶导数，每一期都根据delta值来调整投资策略。Heston模型、BCC模型都可通过计算delta值来调整股票头寸对冲风险。在波动率为常数的假设下，Leland根据交易费用的比例相应的调整波动率改进了对冲误差。[7]Boyle等人在Cox-Ross-Rubinstein 二叉树定价模型的基础上研究了考虑交易费用的期权对冲问题。[8]Nguyen等人研究了考虑随机波动率和交易费用的期权对冲问题，改进了Leland调整波动率的方法。[9]

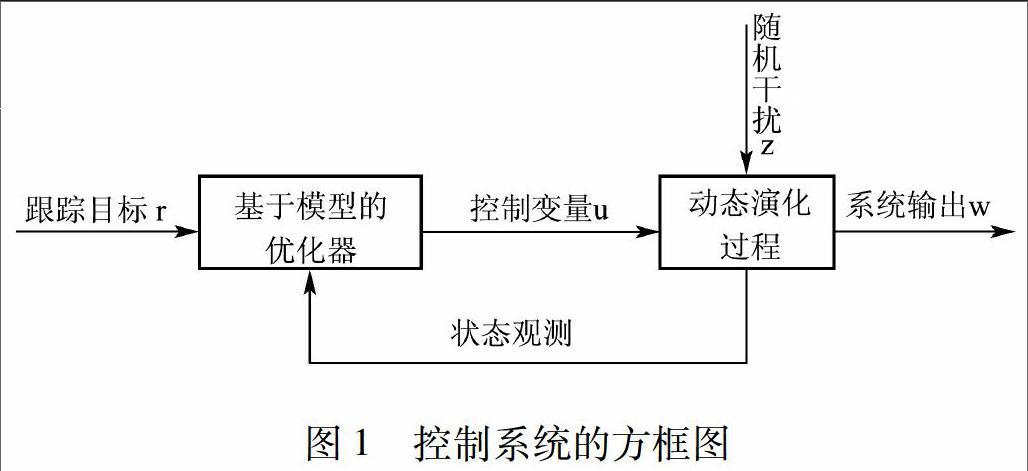
从控制论的角度可以将期权动态对冲看成一个跟踪控制问题。从市场上得到的标的股票价格、利率、期权价格等公开信息看作系统的观测值，系统的控制变量为股票、债券的投资金额或者投资份数，系统的输出变量为由股票和债券构成的投资组合价值，系统的控制目标是在给定投资组合的初始金额等于卖出期权价格的条件下，采用合适的控制方法使得投资组合动态跟踪期权的价值，跟踪误差越接近零越好，且尽可能地排除随机因素的干扰。该系统的方框图如图1所示。

控制论中的随机最优控制可以解决多阶段的期权对冲问题，通过哈密顿-雅可比-贝尔曼（Hamilton-Jacobi-Bellman）偏微分方程来求解。Gondzio和Zhao等人分别把定价和对冲问题转化成随机线性规划问题，通过多阶段随机规划求解。[10-11]这种方法的主要不足是模拟树的节点会随着仿真周期的数量呈现指数倍增长，因此通常情况下每个节点只考虑2个或者3个分叉情况。Primbs把对冲问题转化成一个线性二次型（LQR）调控问题，采用两种方法考虑交易费用，一是在目标函数中加入交易成本作为惩罚项，将对冲问题转化为无约束的随机线性二次型问题；[12]另一种方法是通过随机模型预测控制来处理交易费用约束，求解一个有限时域的二次规划问题。[13]Bemporad等人提出了基于情景树模拟的随机模型预测控制方法，将期权到期时的系统状态映射到较短时刻，根据考虑交易费用与否选择跟踪误差的方差或者条件在险价值（Condition Value at Risk，CVaR）作为目标函数，应用相应的优化方法得到了一个次优解。[14-15]尹力博等人研究了人民币外汇期权的对冲问题，考虑不同资产收益率的随机波动与汇率的随机波动，构建整体风险控制和后验优化风险再调整的外汇期权组合风险综合管理机制，通过基于离散情景树的多阶段随机规划求解最优对冲策略。

上述关于期权对冲问题的研究工作考虑随机波动率风险的比较多，而考虑随机利率和跳跃风险的较少。本文选择随机波动率、随机利率和跳跃风险的BCC模型作为股票价格的预测模型研究欧式期权的动态对冲问题。在不考虑交易费用的情况下，建立以跟踪误差的方差最小化为控制目标的优化控制模型。在考虑交易费用的情况下，建立以跟踪误差的CVaR最小化为控制目标的优化控制模型。并且，通过蒙特卡洛仿真对基于随机模型预测控制的对冲方法和delta对冲方法的效果进行对比分析。进一步使用华夏上证50ETF期权合约的实际数据进行实证分析，结果验证了基于随机模型预测控制方法解决期权对冲问题的有效性。

一、构建资产价格变动模型

（一）股票价格模型

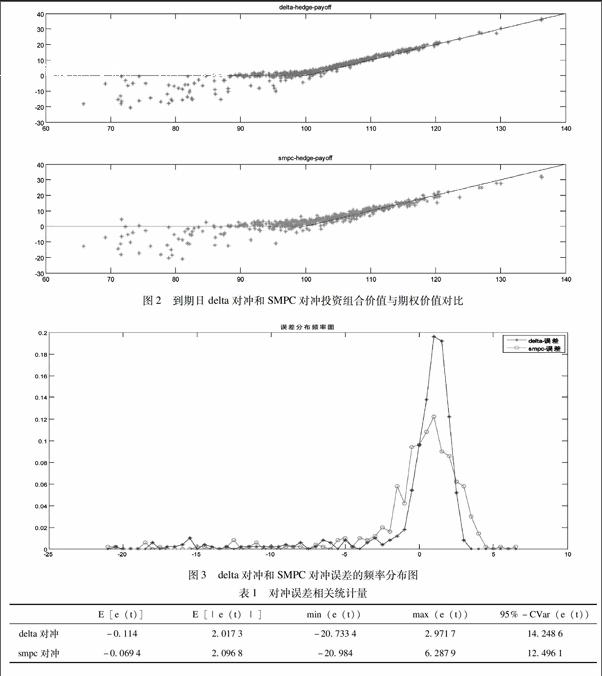
通过图2可以看出，delta对冲和SMPC对冲两种方法整体上能达到跟踪期权回报的目标，但是当期权处于虚值状态时跟踪误差较大；从图3可以看出SMPC对冲的误差分布相对均匀，而delta对冲的误差分布左偏。表1中CVaR统计量的结果表明SMPC对冲的风险要小于delta对冲的风险。

接下来进行考虑交易费用的仿真，设定股票价格变动服从BSM模型，并且预测模型也是BSM模型，以跟踪误差的95%-CVaR为目标函数。设置模型中的参数如下：初始价格S0=100，敲定价格K=100，到期日T=10/360年，无风险利率r=005，波动率sigma=03，仿真步长M = 10，交易费用比率ε设置为1%，总共仿真500次。