EFFECTS OF A TOXICANT ON A SINGLE-SPECIES POPULATION WITH PARTIAL POLLUTION TOLERANCE IN A POLLUTED ENVIRONMENT∗†

Jiamin Liu，Fengying Wei，‡，Stefan A.H.Geritz

（1.College of Math.and Computer Science，Fuzhou University，Fujian 350116，PR China；

2.Dept.of Math.and Stat.，University of Helsinki，Helsinki 00014，Finland）



EFFECTS OF A TOXICANT ON A SINGLE-SPECIES POPULATION WITH PARTIAL POLLUTION TOLERANCE IN A POLLUTED ENVIRONMENT∗†

Jiamin Liu1，Fengying Wei1，2‡，Stefan A.H.Geritz2

（1.College of Math.and Computer Science，Fuzhou University，Fujian 350116，PR China；

2.Dept.of Math.and Stat.，University of Helsinki，Helsinki 00014，Finland）

Abstract

We study a model for the long-term behavior of a single-species population with some degree of pollution tolerance in a polluted environment.The model consists of three ordinary differential equations：one for the population density，one for the amount of toxicant inside the living organisms，and one for the amount of toxicant in the environment.We derive sufficient conditions for the persistence and the extinction of the population depending on the exogenous input rate of the toxicant into the environment and the level of pollution tolerance of the organisms.Numerical simulations are carried out to illustrate our main results.

Keywordssingle-species population；pollution tolerance；toxicant；persistence；extinction；long-term behavior

2000 Mathematics Subject Classification 34D05；92B05

1　Model Formulation

Hallam et al.［1-3］proposed a deterministic model to describe the effects of a toxicant in the environment on a single species population.In their model they assumed that the environment is constant and that the population growth rate depends linearly on the concentration of the toxicant present inside the organisms. Later modifications of the model（see［4-18］and references therein）introduced nonlinearities into the population growth rate as a function of the toxicant concentration as well as fluctuating parameters representing a variable environment.In this paper we present a version of the model with a variable environment as well as a partial pollution tolerance to the toxicant.Our main aim is to study the effect of differentlevels of pollution tolerance on the long-term survival of the population in an environment with a varying input rate of the toxicant into the environment.

We consider a spatially well-mixed population of identical individuals.The model contains three state variables：the population biomass x（t）at time t，the concentration Co（t）of the toxicant present in the organisms（that is，amount of toxicant per biomass），and the concentration Ce（t）of the toxicant in the environment.The rate of change of the biomass at time t is described by the following differential equation： where b and d represent the birth and death rates in the absence of the toxicant respectively；α and β are the population responses to the toxicant in the organisms and in the environment respectively；c is the competition strength among the individuals of population；and the term describes lossesdue to not being possessed pollution tolerance；the itemdenotes the Holling type II functional response where γ represents the pollution tolerance；b，d，α，β，γ，a and c are all positive constants.

The total amount of toxicant present in the organisms is x（t）Co（t）.The rate of change of x（t）Co（t）depends on uptake and loss and is given by the following equation：

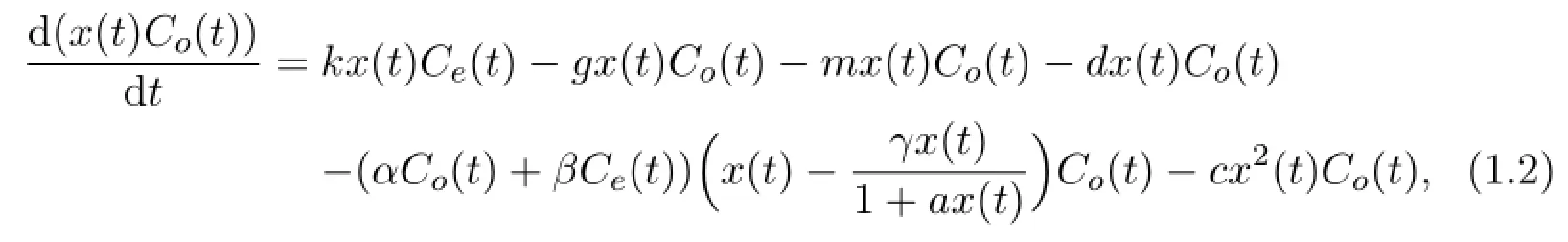
where kx（t）Ce（t）is the toxicant uptake rate from the environment by the population.The toxicant is lost from the organisms due to a number of causes：gx（t）Co（t）describes loss due to egestion；mx（t）Co（t）describes loss due to metabolic processes；dx（t）Co（t）denotes loss due to death of population；（αCo（t）+βCe（t））(x（t）-represents loss due to partial pollution tolerance inside and outside the organisms；cx（t）Co（t）represents loss due to intra-competition of population. Substituting（1.1）into（1.2）yields

Let mobe the mass of per capita and mebe the total mass of the medium in the environment.Then meCe（t）is the total amount of the toxicant in the environment at time t，denoting it by ye（t）.The losses of the toxicant from the environment include the part taken up by population at a rate kmox（t）Ce（t）as well as purification of the environment at a rate hye（t）.The increases of the toxicant in the environment con-sist of four parts：U（t）is the rate of exogenous toxicant input into the environment at time t；the other three parts are gmx（t）C（t），dmx（t）C（t）and（αC（t）+which have already been mentioned in（1.2）.Then

Division of the above equation by megives

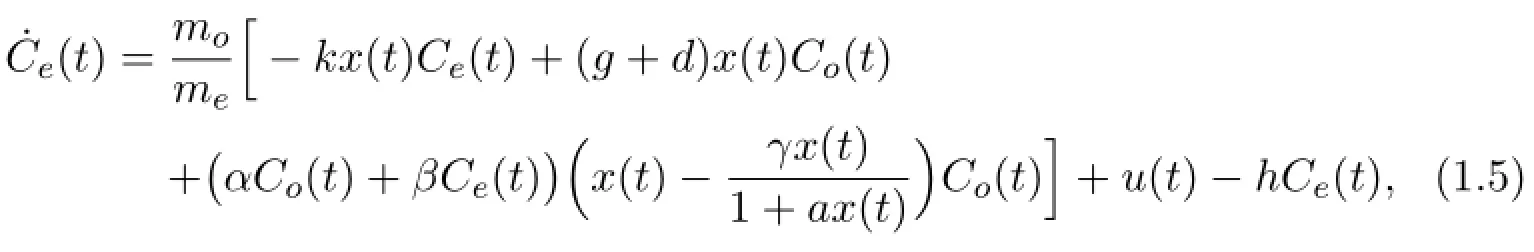
Equations（1.1），（1.3）and（1.5）together with the initial conditions x（0）＞0，Co（0）≥0 and Ce（0）≥0，can be referred to as the following model（M）：

In the case γ=0，our model reduces to the model for which the uniform persistence，weak persistence in the mean and the extinction of the population was investigated in［18］.The main aim of this paper is to find out what are the effects of the pollution tolerance on the long-term behavior of the population.

2　Preliminaries

Throughout this paper we assume that：

（A1）The pollution tolerance of the organisms does not exceed one，that is，γ≤1.

（A2）The exogenous toxicant input into the environment per unit mass is less than the purification rate of the medium in the environment，that is

（A3）The toxicant absorption rate from the environment by the population should be restricted to a given open interval in order to facilitate the proof in next section，that is，for instance，k∈（g+d+α+β，g+m+b）.

We will use the following notations：

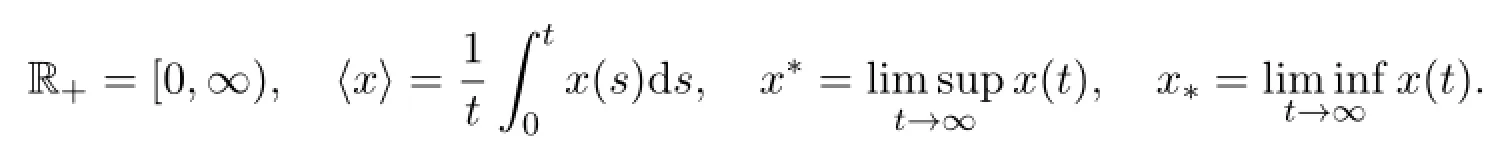
The dynamical behaviors of model（M）will be discussed for a region

Definition 2.1［18］then x（t）is called locally extinctive.If there exist positive constants m and M，such that 0＜m≤x（t）≤M＜∞，then x（t）is called persistent.

Lemma 2.1 For any initial values x（0）＞0，0≤Co（0）＜1 and 0≤Ce（0）＜1， the solution of model（M）is bounded，and it will stay in the domain

Proof By the comparison theorem and the first expression of model（M），we getExpressions（1.3）and（1.5）yield

therefore，the trajectory of model（M）can not cross any coordinate plane in the domain

Next，we will show that the solution is bounded.From now on，this proof goes by contradiction.If it were not true，then there must exist a maximal interval［0，T］such that 0≤Co（t）＜1，0≤Ce（t）＜1 for all t∈［0，T），and follow three possible cases：（i）Ce（T）=1，Co（T）＜1；（ii）Co（T）=1，Ce（T）＜1；（iii）Co（T）=Ce（T）=1.

If case（i）is valid，by the expression（1.5），one can obtain that

According to the continuity of the function Ce（t），there exists a δ＞0，when t∈［T，T+δ］，it follows that Ce（t）≤1.But，it contradicts the assumption that the interval［0，T］is the maximal interval.If case（ii）holds，by（1.3），together with the assumption，we can get

which is also a contradiction.If case（iii）is valid，according to the similar arguments with cases（i）and（ii），the expressions（1.3）and（1.5）give

Similarly we can easily obtain a contradiction.Therefore，the solution of model（M）is bounded.It then follows that 0≤ x（t）≤ c-1（b-d），0≤ Co（t）＜ 1，0≤Ce（t）＜1 for all t≥0.The proof is complete.

3　Main Results

Theorem 3.1 For model（M），if the exogenous input rate of the toxicant into the environment for per unit mass satisfies

then the single-species population is persistent.

Proof We take time average on both sides of the second and the third equations of model（M），then

From this，the proof goes by contradiction.If the single-species population tends to extinction，by Lemma 2.1 and the known conditions 0≤Co（t）＜1，0≤Ce（t）＜1，it follows that the components with x will tend to zero when t approaches infinity. Taking the superior limit on both sides of the expressions（3.1）and（3.2）yield that

Next，we take time average to the first equation of model（M）and get that

taking the superior limit on both sides of（3.4），together with（3.3）and condition of Theorem 3.1，we obtain that

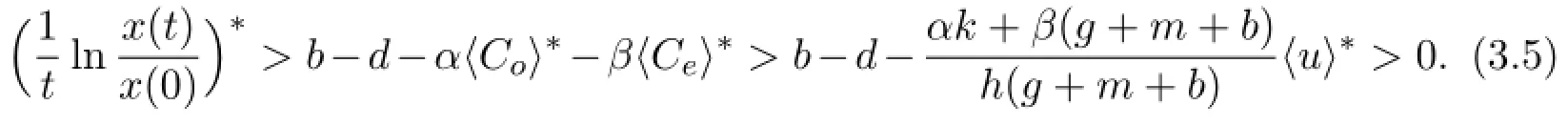
Since the single-species population x（t）goes to extinction when t tends to infinity，the left-hand side of（3.5）is negative.This contradicts the expression（3.5）. The proof is complete.

Theorem 3.2 For model（M），if the exogenous input rate of the toxicant into the environment for per unit mass satisfies

then the single-species population is extinct.

Proof By taking time average of the first equation of model（M）gives

This together with the expression（3.4）leads to

Substitute this into〈Ce〉expressed in（3.1）and deduce that

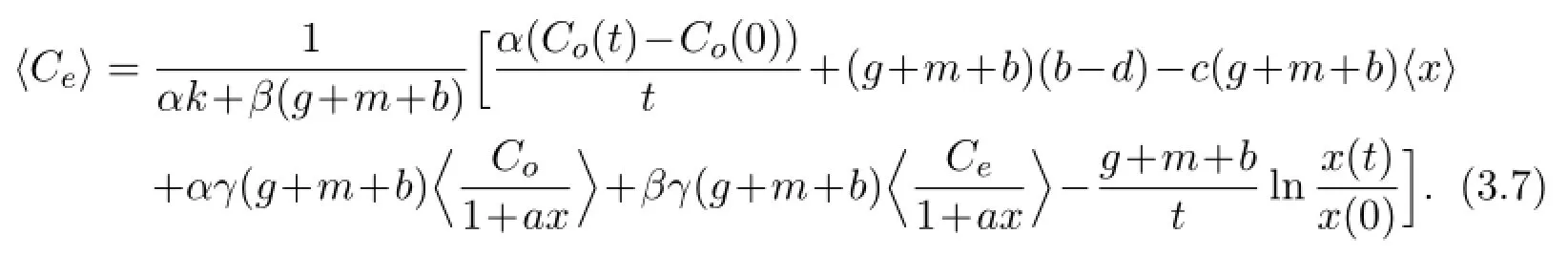
Again，substituting（3.6）and（3.7）into the expression〈u〉derived in（3.2）implies that

From this，the proof will go by contradiction.We assume that the single-species population x（t）is not extinct，say，0＜x（t）≤c，where c is a constant，it then follows that these items with factorhave limit zero.Due to the upper bound 1 for Ceand Coas well asfor any positive x，those items with component Coor Ceor both could be estimated by〈x〉.Take the inferior limit for（3.8）and get that

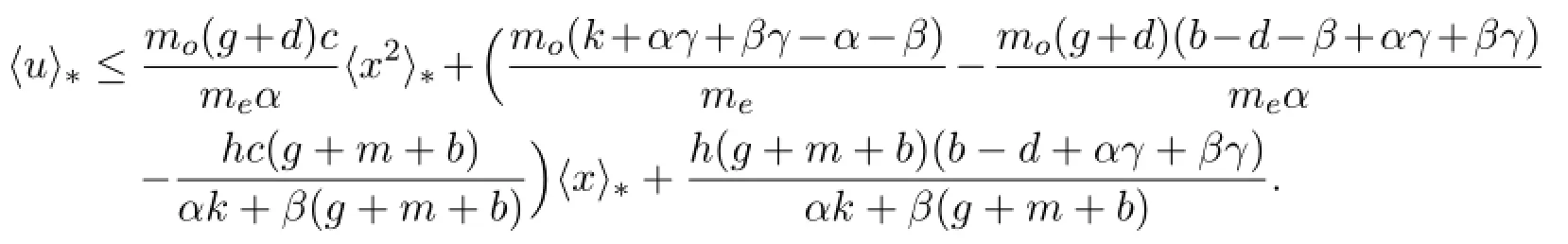
We denote

Since the first item coefficient of F（x）is positive，we take the maximal value at 0 or，that is，

This contradicts the condition of Theorem 3.2.The proof is complete.

4　Numerical Simulations

For model（M），let b=0.5，d=0.1，α=0.2，β=0.3，γ=0.05，k=0.8，g=0.15，mo=1，me=1000，m=0.4，c=0.01，a=2 throughout this section.We set h=0.8 and u（t）=0.5+0.1cost+0.15sin These together with the initial values（5，0.3，0.5）imply

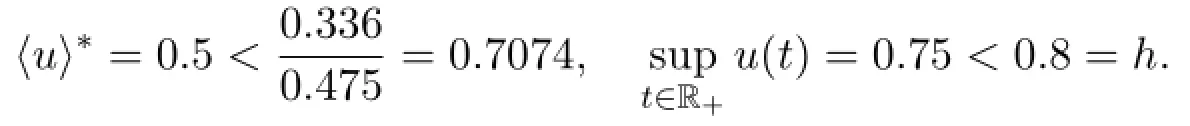
Thus Theorem 3.1 is satisfied，therefore，the single-species population x（t）is persistent，which is shown in Figure 1.If we take u（t）=0.78+0.005cost+0.005sinwith the initial values（30，0.35，0.5），then the following expressions

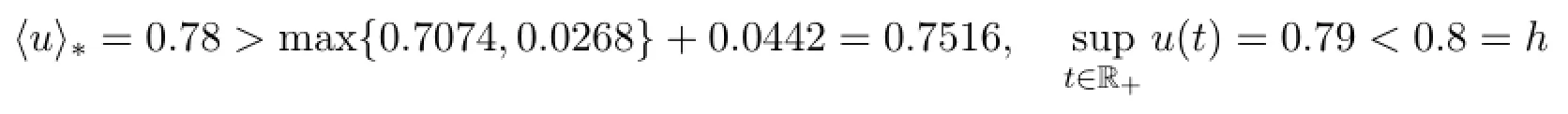
are valid，therefore Theorem 3.2 is satisfied again.So x（t）tends to extinction when the time t tends to large enough，which is shown in Figure 2.

By the similar argument，when h=0.5，together with the initial values（10，0.4，0.6），we assume that u（t）=0.2+0.1cost+0.1sinAccording to the condition of Theorem 3.1，it is easy to check that

then the single-species population x（t）is persistent（see Figure 3）.Set the initial values（35，0.5，0.4）and u（t）=0.48+0.01cost+0.01sin4t with h=0.5，which gives that

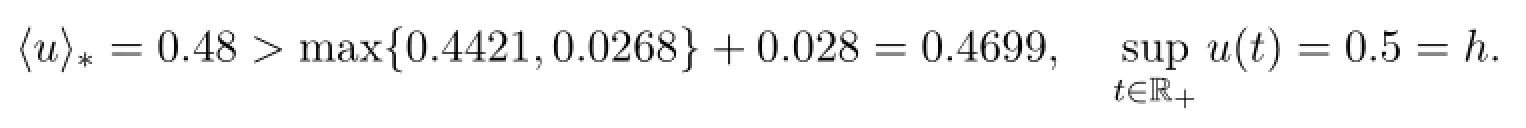
By Theorem 3.2，the single-species population x（t）is extinct for the long time scale（see Figure 4）.

Figure 1：（x（0），Co（0），Ce（0））=（5，0.3，0.5）

Figure 2：（x（0），Co（0），Ce（0））=（30，0.35，0.5）

Figure 3：（x（0），Co（0），Ce（0））=（10，0.4，0.6）

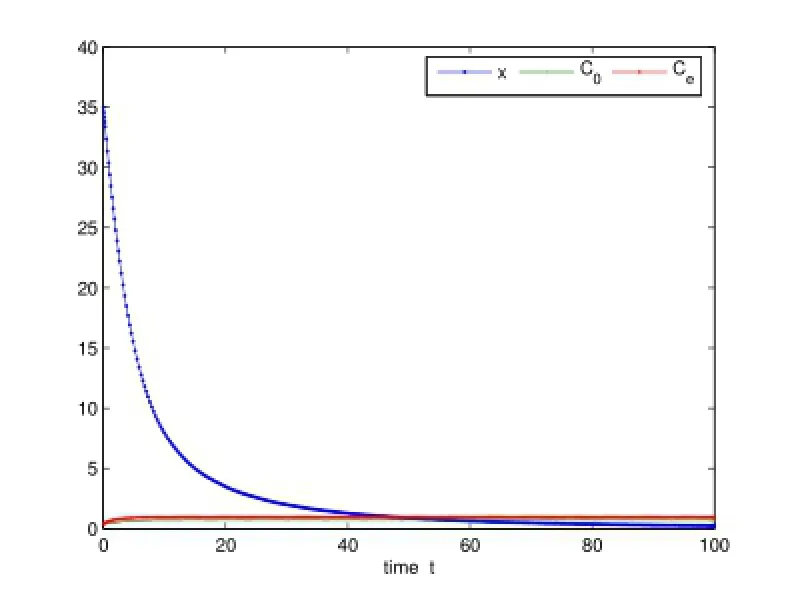
Figure 4：（x（0），Co（0），Ce（0））=（35，0.5，0.4）

5　Conclusions

In this paper，we explore a single-species population model with some degree of pollution tolerance in a polluted environment.The persistence and the extinction of the solutions to the population in model（M）are derived if some moderate conditions are valid.And，our results depend on the exogenous input rate of the toxicant into the environment as well as the pollution tolerance parameter.When we fix all parameters in model（M）except for the pollution tolerance，the results show that the persistence does not change when the pollution tolerance parameter varies from 0.05 to 0.1，the dynamical behavior can be seen in Figure 1.

Especially，in Theorem 3.2，we modify the condition of the extinction corresponding to the population comparing with the one obtained in［18］.In other words，the modification includes the pollution tolerance of the organisms as a component of the sufficient condition，that is，the tolerance-dependent item is a new element of the criterion when the extinction of the single-species population is investigated.On the other hand，the results also show that the threshold of extinction of the population is enhanced in Theorem 3.2 when the pollution tolerance increases.Moreover，the human being might control the persistence of the single-species population to prevent extinction.

References

［1］T.G.Hallam，C.E.Clark，R.R.Lassiter，Effects of toxicants on populations：a qualitative approach I.Equilibrium environmental exposure，Ecol.Model.，18：3-4（1983），291-304.

［2］T.G.Hallam，C.E.Clark，G.S.Jordan，Effects of toxicants on populations：a qualitative approach II.First order kinetics，J.Math.Biol.，18：1（1983），25-37.

［3］T.G.Hallam，J.T.De Luna，Effects of toxicants on populations：a qualitative approach III.Environmental and food chain pathways，J.Theor.Biol.，109：3（1984），411-429.

［4］T.G.Hallam，Z.E.Ma，Persistence in population models with demographic fluctuations，J.Math.Biol.，24：3（1986），327-339.

［5］T.G.Hallam，Z.E.Ma，On density and extinction in continuous population models，J. Math.Biol.，25：2（1987），191-201.

［6］Z.E.Ma，B.J.Song，T.G.Hallam，The threshold of survival for systems in a fluctuating environment，Bull.Math.Biol.，51：3（1989），311-323.

［7］B.Dubey，Modelling the effect of toxicant on forestry resources，Indian J.Pure Appl. Math.，28：1（1996），1-12.

［8］D.M.Thomas，T.W.Snell，S.M.Jaffar，A control problem in a polluted environment，Math.Biosci.，133：2（1996），139-163.

［9］Z.R.He，Z.E.Ma，The survival analysis for Gallopin's system in a polluted environment，Appl.Math.Mech.，21：8（2000），921-928.

［10］Z.R.He，Z.E.Ma，On the effect of pollution and catch to a Logistic population，J. Biomath.，12：3（1997），230-237.

［11］J.W.He，Effect of pollution tax on population in a polluted environment，Math.Method. Appl.Sci.，34：12（2011），1440-1444.

［12］S.L.LV，J.D.Zhao，Dynamical behavior of a single-species population model in a polluted environment，J.Biomath.，29：4（2014），586-596.

［13］H.I.Freedman，J.B.Shukla，Models for the effect of toxicant in single-species and predator-prey systems，J.Math.Biol.，30：1（1991），15-30.

［14］B.Buonomo，A.D.Liddo，I.Sgura，A diffusive-convective model for the dynamics of population-toxicant interactions：some analytical and numerical results，Math.Biosci.，157：1-2（1999），37-64.

［15］L.Bai，K.Wang，A diffusive stage-structured model in a polluted environment，Nonlinear Anal.：Real World Appl.，7：1（2006），96-108.

［16］M.Liu，K.Wang，X.W.Liu，Long term behaviors of stochastic single-species growth models in a polluted environment，Appl.Math.Model.，35：2（2011），752-762.

［17］M.Liu，K.Wang，Persistence and extinction of a stochastic single-specie model under regime switching in a polluted environment，J.Theor.Biol.，264：3（2010），934-944.

［18］J.W.He，K.Wang，The survival analysis for a single-species population model in a polluted environment，Appl.Math.Model.，31：10（2007），2227-2238.

（edited by Mengxin He）

∗Supported by National Natural Science Foundation of China（No.11201075），Natural Science Foundation of Fujian Province（No.2016J01015）and Scholarship under Education Department of Fujian Province.

†Manuscript received October 17，2015；Revised February 29，2016

‡Corresponding author.E-mail：weifengying@fzu.edu.cn