SCALE-TYPE STABILITY FOR NEURAL NETWORKS WITH UNBOUNDED TIME-VARYING DELAYS∗†

Liangbo Chen，Zhenkun Huang

（School of Science，Jimei University，Fujian 361021，PR China）



SCALE-TYPE STABILITY FOR NEURAL NETWORKS WITH UNBOUNDED TIME-VARYING DELAYS∗†

Liangbo Chen，Zhenkun Huang‡

（School of Science，Jimei University，Fujian 361021，PR China）

Abstract

This paper studies scale-type stability for neural networks with unbounded time-varying delays and Lipschitz continuous activation functions.Several sufficient conditions for the global exponential stability and global asymptotic stability of such neural networks on time scales are derived.The new results can extend the existing relevant stability results in the previous literatures to cover some general neural networks.

global asymptotic stability；global exponential stability；neural networks；on time scales

2000 Mathematics Subject Classification 92B20

1　Introduction

Consider a general class of neural networks with unbounded time-varying delays on time scales：

where xi（t）corresponds to the state of the ith unit at time t∈T，fj（xj）and gj（xj）are the activation functions of the jth unit，ci＞0 represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network，τij（t）corresponds to the transmission delay which satisfies τij（t）≥0，aijand bijdenote the strength of the jth neuron on ith unit at time t and t-τij（t），i，j∈N，where N=｛1，2，···，n｝.In this paper，we make some basic assumptions：

1）fi（0）=gi（0）=0；

2）There exist constants li＞0，ki＞0 such that for any r1，r2，r3，r4∈R

For any t0≥0，the initial condition of the neural network model（1.1）is assumed to be

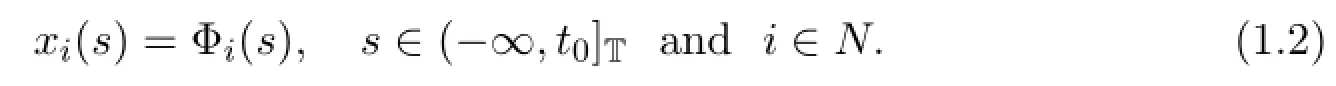
In stability analysis of neural networks，the qualitative properties primarily concerned are the uniqueness，global stability，robust stability，and absolute stability of their equilibria.In［6］and［8］，global asymptotic and exponential stability were given for neural networks without time delays.The case of constant time delay was also studied in［2，7］.In［3，9］，the authors discussed the case of bounded time-varying delay.In addition，the authors in［4］described the case of unbounded time-varying delay，that gave several sufficient conditions for the global exponential stability.In［10］，several algebraic criterions for stability were obtained by constructing proper Lyapunov functions and employing Young inequality.

Recently，people have paid attention to the neural network models on time scales，and some of them have got some important results，such as［11-23］.In［12］，by using the contraction mapping theorem and Gronwall's inequality on time scales，the authors established some sufficient conditions on the existence and exponential stability of periodic solutions of a class of stochastic neural networks on time scales.In［14，16，18］，the authors paid attention to the periodic solutions of a class of neural networks delays on time scales.Based on contraction principle and Gronwall-Bellmans inequality，some new results for the existence and exponential stability of almost periodic solution of a general type of delay neural networks with impulsive effects were established in［15］.The problem on the global exponential stability of neural networks on time scales was considered in［13，22，23］.In［17，19-21］，global exponential stability of networks with time-varying delays on time scales were considered.

In this paper，we consider a general neural network model on time scales.By using different methods，several sufficient conditions for the global asymptotic sta-bility and the global exponential stability of（1.1）are obtained.These results are new and different from the existing ones.

2　Preliminaries

In this section，we first introduce some basic definitions of dynamic equations on time scales.

A time scale is an arbitrary nonempty closed subset of the real numbers.In this paper，T denotes an arbitrary time scale.

Definition 2.1 The forward and backward jump operators respectively are σ：T→T and ρ：T→T such that σ（t）=inf｛s∈T：s＞t｝，ρ（t）=sup｛s∈T：s＜t｝. And the graininessµ：T→R+is defined byµ（t）：=σ（t）-t.Obviously，µ（t）=0 if T=R，whileµ（t）=1 if T=Z.

A point t∈T is said to be left（right）-dense if ρ（t）=t（σ（t）=t）；A point t∈T is said to be left（right）-scattered if ρ（t）＜t（σ（t）＞t）.If T has a left-scattered maximum o then we let Tκ：=T/｛o｝，otherwise Tκ：=T.

Definition 2.2 Let f：T→R and t∈Tκ.fΔ（t）is said to be the Δ-derivative of f（t）if and only if for any ϵ＞0，there is a neighborhood Ξ of t such that

D+fΔ（t）is said to be the Dini derivative of f（t）if given ϵ＞0，there exists a right neighborhoodof t such that

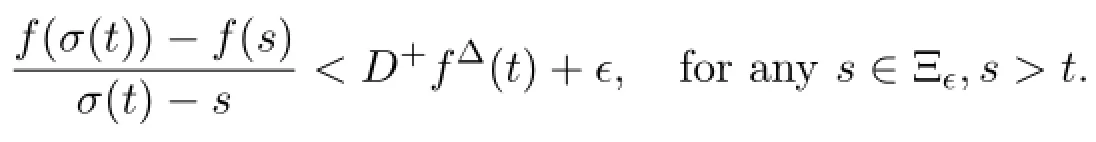
Definition 2.3 A function f：T→R is called rd-continuous if it is continuous in right-dense points and the left-sided limits exist in left-dense points，while f is called regressive if 1+µ（t）f（t）0.

Denote R by the set of all regressive and rd-continuous functions，if f∈R and 1+µ（t）f（t）＞0，then we write f∈R+.Let p∈R，the exponential function is defined by

with the cylinder transformation

If p∈R，fix t0∈T.Then ep（·，t0）is a solution of the initial value problem

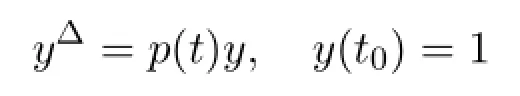
on time scale T.

Lemma 2.1 If p∈R，then

（i）e0（t，s）≡1 and ep（t，t）≡1；

（ii）ep（σ（t），s）=eσp（t，s）=（1+µ（t）p（t））ep（t，s）；

（iii）ep（t，s）ep（s，r）=ep（t，r）；

（iv）ep（t，s）eq（t，s）=ep⊕q（t，s）；

（v）ep（t，s）==e⊖p（s，t）；

Definition 2.4（1.1）is said to be global asymptotically stable（GAS），if it is locally stable in the sense of Lyapunov and is globally attractive.In addition，（1.1）is said to be globally exponentially stable（GES），if there exist constants α＞0，β＞0 such that the solutions x（t）of（1.1）with any initial condition（1.2）satisfies

3　Main Results

Theorem 3.1 If there exist ωi＞0 and ηi∈Crdwith 0＜1+µ（t）ηi（t）＜1 and

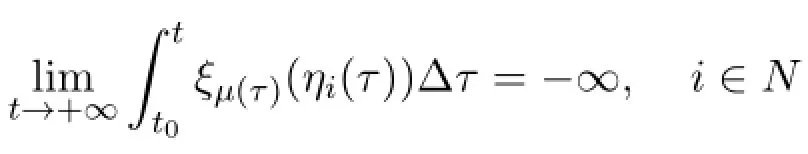
such that

then（1.1）is GAS.If there exist γ＞0，β＞0 such that for any i∈N，eηi（t，t0）≤γeβ（t0，t），then（1.1）is GES.

Proof Let

It follows from（1.1）that

Let

For t∈Tκ，denote

where εi∈Crdand 0＜1+µ（t）εi（t）＜1，i∈N.Let

Then we assert that ϕi（t）≤0，for any t∈［t0，+∞）T.Otherwise，due to ϕi（t）≤0 for t∈（-∞，t0］T，there exist a subset N⊥N and a first time t1≥t0such that

From（3.2），one has

Since ϕm（t1）≥0，we get that zm（t1）≥v（t0）eεm⊕ηm（t1，t0）.Hence there must exist κ＞0 such that

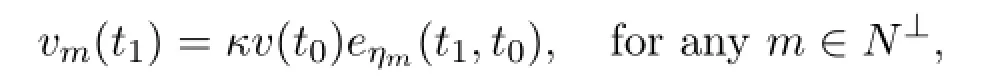
which leads to

From the fact 1+µ（t）ηj（t）∈（0，1），for any t∈［t0，+∞）T，we get ξµ（t）（ηj（t））≤ηj（t）and hence

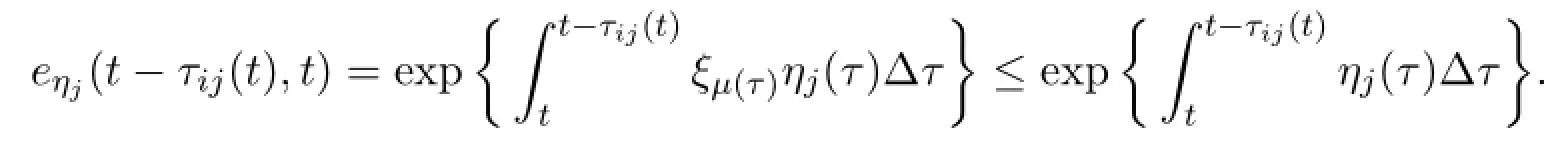
Together with（3.1），one has

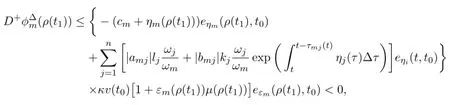
which contradicts（3.3）.Hence，for any t≥t0and i∈N，

that is，（1.1）is GAS.If there exist γ＞0，β＞0 such that eηi（t，t0）≤γeβ（t0，t），then（1.1）is GES.The proof is complete.

Remark 3.1 The assumption 0＜1+µ（t）ηi（t）＜1 is a necessary condition for the global exponential stability of（1）on time scales.Otherwise，if 1+µ（t）ηi（t）≥1 and v（t0）＞0，we can get v（t0）eηi（t，t0）→∞when t→∞，then（1）is not globally exponentially stable.

In the following discussion，we denote τij（t）=τ（t），for all i，j∈N.By the method different from Theorem 1.1，we also can get the general global stability analysis of neural networks as follows.

Theorem 3.2 Let

where ω＞0 is a positive constant，i∈N.If

where λ（t）=M22eM21（t-τ（t），σ（t））and 0＜1+µ（t）M21＜1，then（1.1）is GAS. If there exist γ＞0，β＞0 such that

then（1.1）is GES.

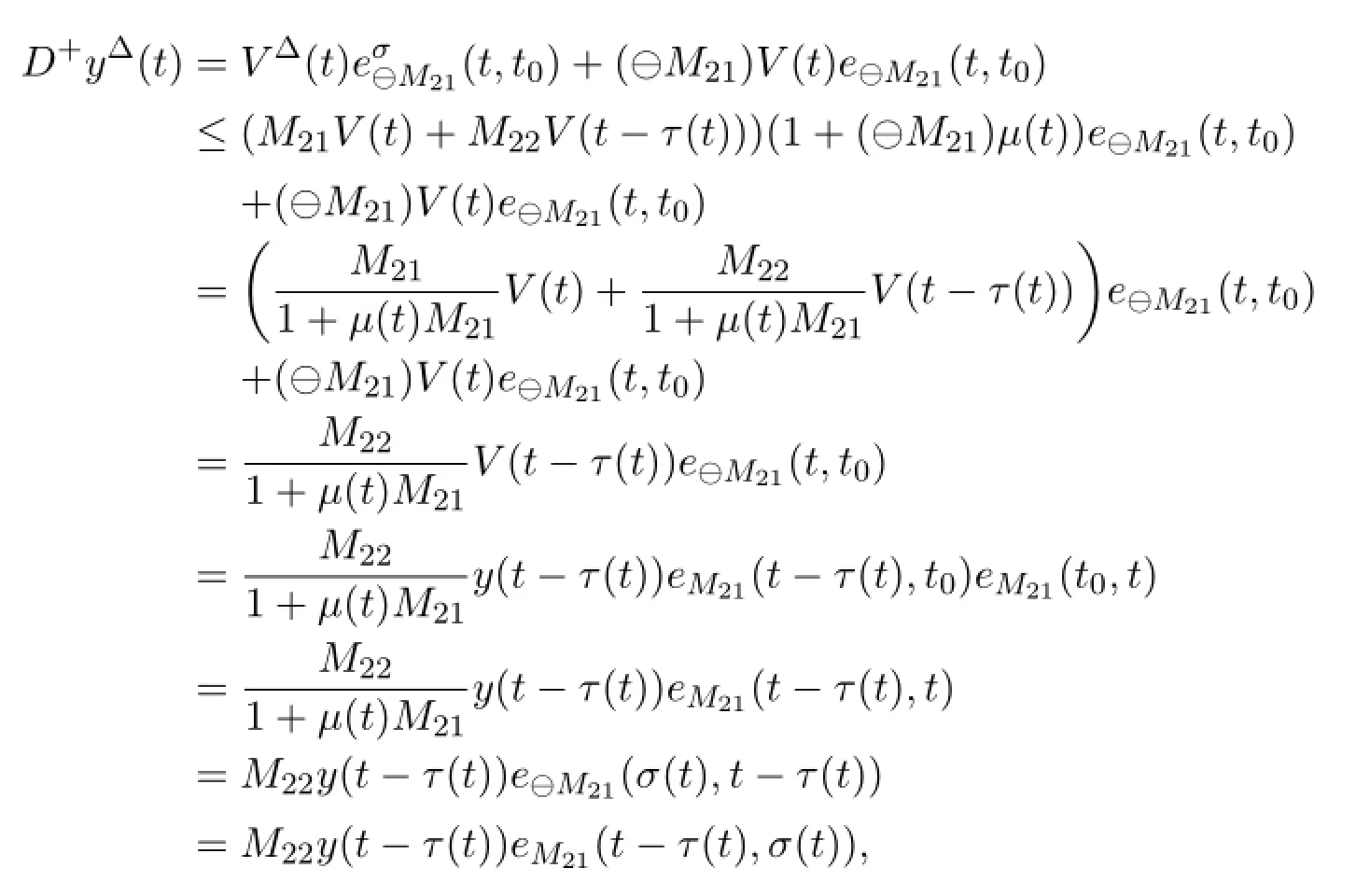
hence

Define an auxillatory function

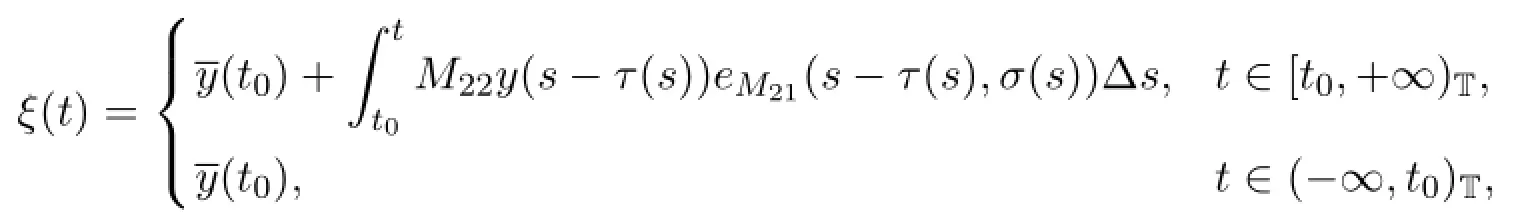
then it follows from M22≥0 and y（t）≥0 that ξ（t）is a monotone increasing function and

By（3.6）and 0＜1+µ（t）M21＜1，we know y（t）≤ξ（t）for any t∈T.Hence y（t-τ（t））≤ξ（t-τ（t））≤ξ（t）which leads to

It follows from（3.7）that

Then we can get

and

where t∈［t0，+∞）T.The proof is complete.

Remark 3.2 The assumption 0＜1+µ（t）M21＜1 is necessary for the global exponential stability of（1.1）on time scales.Whenis a nonsingular M-matrix，M21＜0 where δij=1，i=j；δij=0，ij.

Using a different Lyapunov function from that in Theorem 3.2，we have following theorems.

Theorem 3.3 For any ωi＞0，oij，pij，qij，rij∈R（i，j∈N），let

then（1.1）is GES.

It follows from（1.1）that

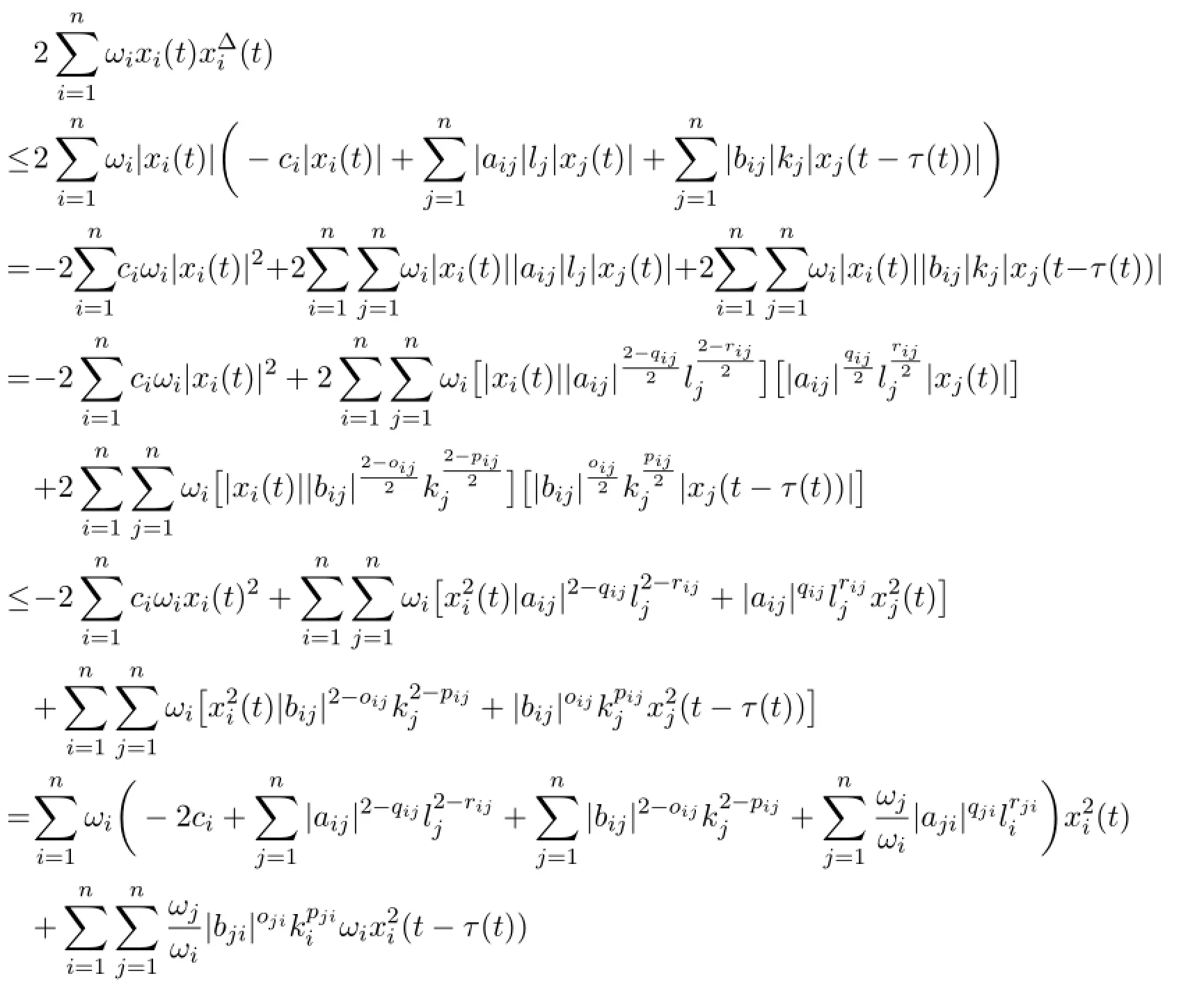
and

Hence，we can get

The remaining proof is similar to the last part of that of Theorem 3.2.

4　Examples

In this section，we will give two numerical examples to illustrate Theorems 3.1 and 3.2.From the definition of V（t）in Theorems 3.2 and 3.3，we can also give a similar example to check Theorem 3.3.But we omit here.

Example 4.1 Consider

where g（x（t））= （1-exp｛-x（t）｝）/（1+exp｛-x（t）｝）.For any t≥ t0＞ 1，let ω1=ω2=1，η1（t）=η2（t）=ε1（t）=ε2（t）=-1/t，l1=l2=k1=k2=1.

（1）Let T=R and τ11（t）=t/2，τ12（t）=2t/3，τ21（t）=3t/4，τ22（t）=4t/5，when t→+∞，from Theorem 3.1 we can get the following formula

and

then（4.1）is GAS.

（2）Let T=Z and τ11（t）=1，τ12（t）=2t，τ21（t）=2t+1，τ22（t）=3t-2，when t→+∞，from Theorem 3.1 we can get the following formula

and

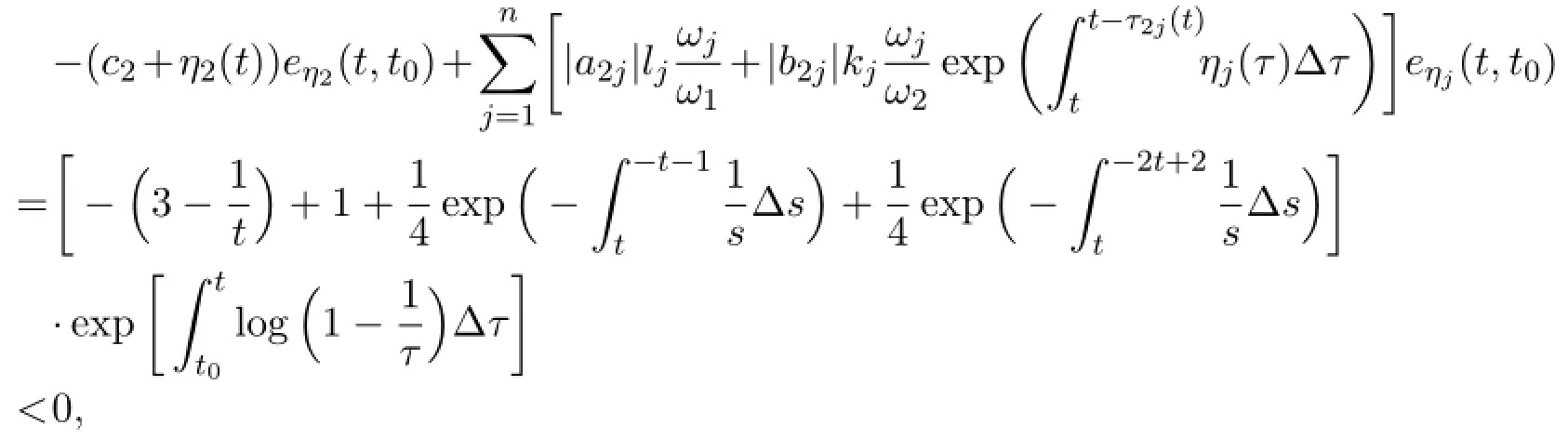
then（4.1）is GAS.

Moreover，according to Theorem 3.1，it's easy to check that（4.1）is also GAS. But Theorems 3.2 and 3.3 cannot be used to ascertain the stability of（4.1）.

Figure 1：（a）The global exponential stability of solution of（4.1）on R.（b）The global exponential stability of solution of（4.1）on Z.

Example 4.2 Consider

where t∈T，f（x（t））=（|x（t）+1|-|x（t）-1|）/2 and

for n∈Z.Obviously，l1=l2=k1=k2=1.Take ω1=ω2，then P21=-1，P22= 1，µ（t）=1/4，when t→+∞，then

Since for any t＞0，

it follows from Theorem 3.2 that（4.2）is GAS.However，the stability of（4.2）can not be determined by Theorem 3.1.

Figure 2：The globally exponential stability of solution of（4.2）on

5　Conclusion Remarks

In this paper，scale-type stability on time scales for neural networks with both general global stability and global exponential stable with unbounded time-varying delays is investigated.We would like to point out that it is possible to apply our main results to some neural networks，such as neural networks with time-varying delays［3，6，9］，neural networks with unbounded time-varying delays［4］.

References

［1］M.Bohner and A.Peterson，Dynamic Equations on Time Scales：An introduction with Applications，Boston，2001.

［2］P.V.D.Driessche and X.Zou，Global attractivity in delayed Hopfield neural network models，SIAM.J.Appl.Math，58（1998），1878-1890.

［3］C.Hou and J.Qian，Stability analysis for neural dynamics with time varying delays，IEEE Trans.Neural Netw.，9（1998），221-223.

［4］Z.Zeng and J.Wang，Global asymptotic stability and global exponential stability of neural networks with unbounded time-varying delays，IEEE Trans.Express Briefs，52（2005），168-173.

［5］M.Bohner and A.Peterson，Advances in Dynamic Equations on Time Scales，Boston，2003.

［6］S.Arik，Global asymptotic stability of a class of dynamical neural networks，IEEE Trans.Circuits Syst.I，Fundam.Theory Appl.，47（2000），568-571.

［7］J.Cao and Q.Li，On the exponential stability and periodic solutions of delayed cellular neural networks，J.Math.Anal.Appl.，252（2000），50-64.

［8］X.Liang and J.Wang，Absolute exponential stability of neural networks with a general class of activation functions，IEEE Trans.Circuits Syst.I，Fundam.Theory Appl.，47（2000），1258-1263.

［9］Z.Zeng and J.Wang，and X.Liao，Global exponential stability of a general class of recurrent neural networks with time-varying delays，IEEE Trans.Circuits Syst.I，Fundam.Theory Appl.，50（2003），1353-1358.

［10］Z.Tu，J.Jian，B.Wang，Positive invariant sets and global exponential attractive sets of a class of neural networks with unbounded time-delays，Communications in Nonlinear Science and Numerical Simulation，16（2011），3738-3745.

［11］S.Hilger，Analysis on measure chains-A unified approach to continuous and discrete calculus，Results Math，18（1990），18-56.

［12］L.Yang and Y.Li，Existence and exponential stability of periodic solution for stochastic Hopfield neural networks on time scales，Neurocomputing，167（2015），543-550.

［13］Q.Song，and Z.Zhao，Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales，Neurocomputing，171（2016），179-184.

［14］H.Zhou and Z.Zhou，Almost periodic solutions for neutral type BAM neural networks with distributed leakage delays on time scales，Neurocomputing，157（2015），223-230.

［15］C.Wang and R.P.Agarwal，Almost periodic dynamics for impulsive delay neural networks of a general type on almost periodic time scales，Communications in Nonlinear Science and Numerical Simulation，36（2016），238-251.

［16］B.Du and Y.Liu，Almost periodic solution for a neutral-type neural networks with distributed leakage delays on time scales，Neurocomputing，173（2016），921-929.

［17］W.Gong and J.Liang，Matrix measure method for global exponential stability of complex-valued recurrent neural networks with time-varying delays，Neural Networks，70（2015），81-89.

［18］T.Liang and Y.Yang，Existence and global exponential stability of almost periodic solutions to Cohen-Grossberg neural networks with distributed delays on time scales，Neurocomputing，123（2014），207-215.

［19］C.Xu and Q.Zhang，Existence and global exponential stability of anti-periodic solutions of high-order bidirectional associative memory（BAM）networks with time-varying delays on time scales，Journal of Computational Science，8（2015），48-61.

［20］Y.Liu and Y.Yang，Existence and global exponential stability of anti-periodic solutions for competitive neural networks with delays in the leakage terms on time scales，Neurocomputing，133（2014），471-482.

［21］B.Zhou and Q.Song，Global exponential stability of neural networks with discrete and distributed delays and general activation functions on time scales，Neurocomputing，74（2011），3142-3150.

［22］L.Li and S.Hong，Exponential stability for set dynamic equations on time scales，Journal of Computational and Applied Mathematics，235（2011），4916-4924.

［23］Z.Zhang and K.Liu，Existence and global exponential stability of a periodic solution to interval general bidirectional associative memory（BAM）neural networks with multiple delays on time scales，Neural Networks，24（2011），427-439.

（edited by Liangwei Huang）

∗This research was supported by National Natural Science Foundation of China under Grant 61573005 and 11361010，the Foundation for Young Professors of Jimei University and the Foundation of Fujian Higher Education（JA11154，JA11144）.

†Manuscript received April 21，2016；Revised June 7，2016

‡Corresponding author.E-mail：hzk974226@jmu.edu.cn