地震力作用下浅埋双侧偏压隧道松动的围岩压力

李栋梁，刘新荣，杨欣，王震，袁文



地震力作用下浅埋双侧偏压隧道松动的围岩压力

李栋梁，刘新荣，杨欣，王震，袁文

(重庆大学土木工程学院，山地城镇建设与新技术教育部重点实验室，重庆，400045)

为了研究水平和竖向地震荷载同时作用时浅埋双侧偏压隧道松动围岩压力的分布，以拟静力法为基本研究方法，推导浅埋双侧偏压隧道围岩松动压力的解析解。根据推导的公式对在水平和竖向地震荷载同时作用时隧道两侧的破裂角的变化规律进行研究。研究研究表明：围岩级别越高，破裂角越小；地面坡度越大，破裂角越大；随着地震烈度增加，隧道两侧的破裂角的变化趋势完全相反，可根据水平地震力的方向或地震力偏角的方向进行判断；对于围岩较差的V和VI级围岩隧道，给出抗震设防烈度分别为VI，VII，VIII和IX度时破裂角加固范围。

拟静力法；地震力；双侧偏压隧道；破裂角；松动围岩压力

偏压隧道是指承受显著偏压荷载(不对称力)的隧道。随着公路隧道建设的不断发展，大量隧道需要穿越山岭地区，由于山势此起彼伏，使得偏压隧道的存在和发展成为必然。由于偏压隧道具有特殊的受力特性，使得其设计和支护等区别于一般隧道。SARI等[1−2]对浅埋单侧偏压小净距隧道的围岩压力计算理论进行了研究。雷明峰等[3]运用弹性力学基本方程，对浅埋单侧偏压隧道衬砌结构应力的动态变化规律和分布形式以及衬砌和围岩的破坏机制进行了系统分析。唐明明等[4]通过建立符合实际地形的三维模型，对不同开挖方式偏压隧道不同位置的塑性区、围岩变形及地表沉降进行了分析，提出了更高效、更经济的开挖方案。刘新荣等[5]根据工程实例，结合现场监控量测资料分析了不良地质情况下偏压隧道支护开裂的主要原因。来弘鹏等[6]以宜巴高速公路卧佛山隧道实体工程为依托，对软岩大变形偏压公路隧道变形与荷载作用特征进行了研究。然而，由于地壳版块活跃，地震灾害时有发生，单纯的静力分析已不能满足人们对偏压隧道的安全性和耐久性的要求，偏压隧道的抗震问题日益突出。为此，SANCHEZ–MERINO等[7]对隧道衬砌对于面波在纵向的简单地震响应进行了研究。蒋树屏 等[8]通过有限元方法计算8种不同埋置深度条件下的偏压隧道地震响应，并对计算模型的地震输入方法进行了验证。徐华等[9]以国道318线黄草坪2号隧道为原型，开展了大型三维振动台模型试验，研究了隧道结构的地震动力响应规律及隧道与围岩的相互动力作用。以往隧道抗震研究都是主要考虑水平地震力作用，现行规范也不例外[10]。而实际的地震加速度是个具有方向不确定性的变量，例如2008年在四川省汶川县发生的强烈地震，竖向地震力的作用同样给很多建筑结构造成破坏。与此同时，受地形条件限制而出现的比单侧偏压隧道更特殊更复杂的双侧偏压隧道也缺乏系统研究。为此，本文作者以浅埋双侧偏压隧道为研究对象，考虑水平和竖向地震力的共同作用，以拟静力法为基本研究方法，结合国内外现有的研究成果，推导出浅埋双侧偏压隧道的围岩松动压力的解析解，并根据推导的公式对水平和竖向地震力共同作用时隧道两侧的破裂角进行探讨。

1 拟静力法

地下空间结构设计计算方法很多，总体上可以分为3类，分别为静力法、拟静力法和动力反应分析 法[11]。其中，静力法计算太简单、粗略，计算结果不够精确，已很少使用；动力反应分析法虽然计算精度高，但由于需要较深的专业知识和技能，对设计师素质要求高且操作繁杂，其计算结果的评价也比较困难，因此，除特别重大的工程项目或很复杂的地质条件下使用外，人们通常使用拟静力法进行计算[12]。

拟静力法的物理概念简单明了，计算步骤便捷，在现实工程实践中得到广泛应用。它是一种近似的用静力方法解决动力学问题的简易方法，其核心思想是将地震荷载的作用效果用水平和竖直方向恒定的惯性力替代，并作用在所研究结构上，惯性力的施加方向取为对结构最不利的方向。

地震动过程中产生的水平方向和竖直方向的惯性力分别为：

式中：h和v分别为水平和垂直方向的拟静力加速度；为水平方向的拟静力加速度系数，在设计地震烈度为Ⅵ，Ⅶ，Ⅷ和Ⅸ度时，其值分别为0.05，0.10，0.20和0.40；为竖直方向的拟静力加速度系数，一般地，v=(1/2~2/3)h；为岩土体重力；为重力加速度。

2 松动围岩压力解析解

2.1 基本假设

根据现行的公路隧道设计规范(JTG D70—2004)[13]，结合浅埋双侧偏压隧道的特点，为了便于计算，进行如下假设：

1) 岩土体为各向同性的均匀连续介质。

2) 水平和竖向地震荷载作用对岩土体的基本物理力学特性不产生较大影响。

3) 隧道左侧的地表倾角为l，右侧的地表倾角为r。在隧道左侧的岩土体中形成破裂面，其与水平面的夹角为破裂角1，在隧道右侧的岩土体中形成破裂面，其与水平面的夹角为破裂角2。

4) 当隧道拱顶上的覆盖岩土体下沉时，将会带动两侧岩土体(如图1中和所示)下沉，而当整个岩土体下沉时，又会受到两侧的未受扰动的岩土体阻止其下沉的阻力作用。

5)斜直面和是人为假设的破裂滑动面，该破裂滑动面的抗剪强度由岩土体的黏聚力和计算摩擦角决定。另外，直面和并非真实的滑动破裂面，是为了便于分析人为假设存在的，所以，其滑面阻力要小于真实的破裂面阻力，其滑面的摩擦角要小于计算摩擦角，当无实测资料时，可从文献[13]中按相关规定选取。

本文是在以上基本假设的基础上，在水平和竖向地震力共同作用的情况下，分析浅埋双侧偏压隧道的松动围岩压力及破裂角。图1所示为地震力作用下浅埋双侧偏压隧道围岩压力计算简图。

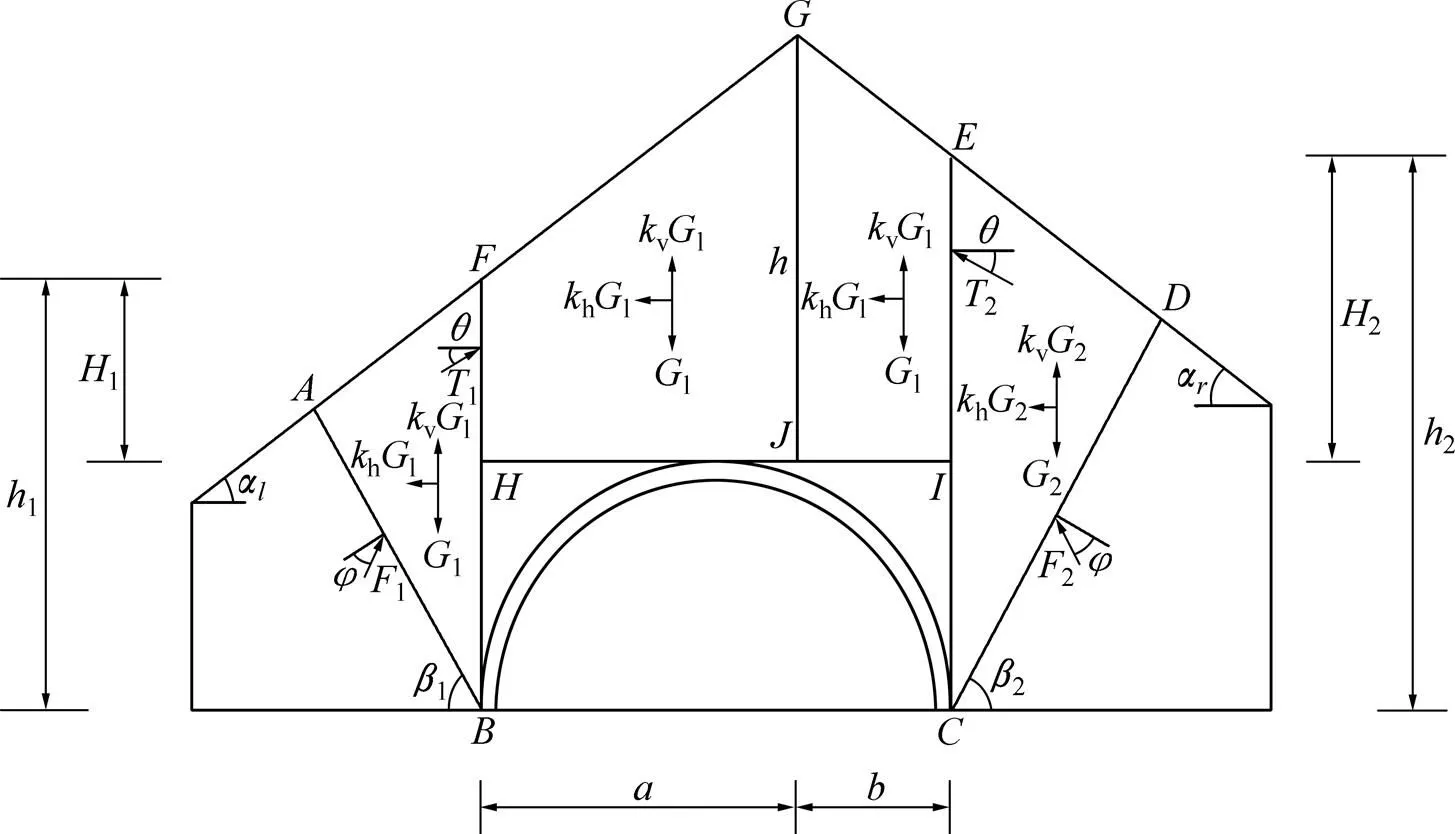
图1 地震力作用下双侧偏压隧道围岩压力计算简图

2.2 隧道左侧侧向水平压力及破裂角

取隧道左侧岩土体为研究对象，其所受荷载及各几何参数如图2所示。由几何关系可知点到的距离1为

设岩土体的容重为，无地震动作用时岩土体的重力为1，则有

地震发生时，岩土体受到地震荷载的影响，根据式(1)和(2)，岩土体的水平方向和竖直方向将分别会产生惯性力h1和v1。受力分析简图如图3(a)所示。隧道与其上覆岩体下沉而带动岩土体下滑时在面上产生的带动下滑力为1，面上的摩阻力为1。

依照拟静力法的要求，将惯性力h1和v1视为静荷载与岩土体重力1进行力的合成，可得到合力1′。其中，1′与铅垂线的夹角为，如图3(b)所示。为地震力偏角，据文献[14]，有

根据几何关系易知：

(a) 原始受力图；(b) 惯性力与重力合成；(c) 力系旋转角度

图3 岩土体受力分析简图

Fig. 3 Calculation diagrams of rock mass

为使合力1的方向沿竖直方向便于计算，将图3(b)逆时针旋转角度，如图3(c)所示。由于这种旋转未改变力系的平衡及各力之间的几何关系，不会改变侧向水平压力的计算结果。

由三角函数变换可知：

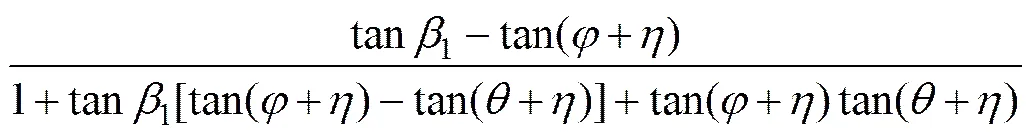
将式(4)和(6)代入(10)，可得：

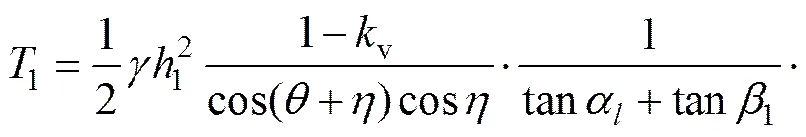
(11)

令1为隧道左侧侧压力系数为，则

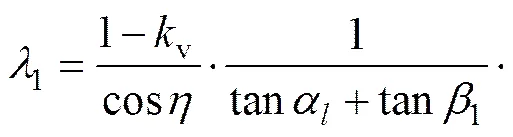
(12)

将式(12)代入式(11)并化简可得

由式(12)可知1为，，和1的函数。在一般情况下，式中除1外皆为已知，所以，1只是随着1的变化而变化。1为假设的滑动破裂面与隧道底部的水平面之间的夹角，并非极限状态下的自然破裂角，其最可能存在的位置必然是1为最大值时的位置，为此，应利用求极值的方法来求得1。

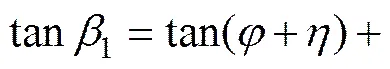
式中：为面的计算摩擦角，为面的摩擦角，且＜。由文献[13]知可由确定。易知1可由，和l确定。

据文献[13]，隧道左侧水平向侧压力为

2.3 隧道右侧侧向水平压力及破裂角

取隧道左侧岩土体为研究对象，其重力为2，隧道与其上覆岩体下沉而带动岩土体下滑时在面上产生的带动下滑力为2，面上的摩阻力为2，其荷载及各几何参数如图4所示，其受力分析简图如图5所示。

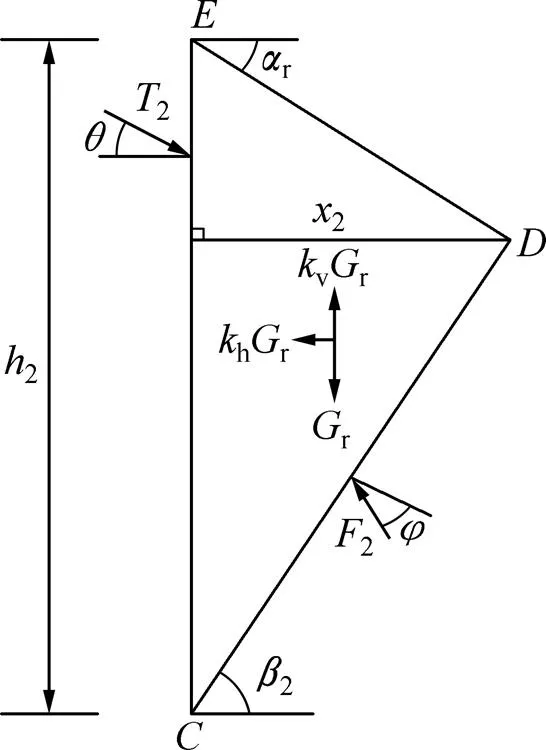
图4 岩土体CDE受力图

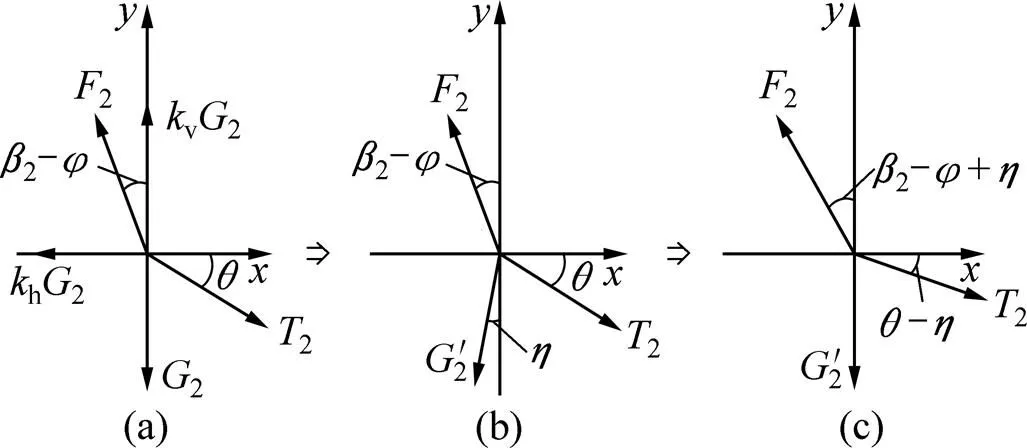
(a) 原始受力图；(b) 惯性力与重力合成；(c) 力系旋转角度η

同理可知：

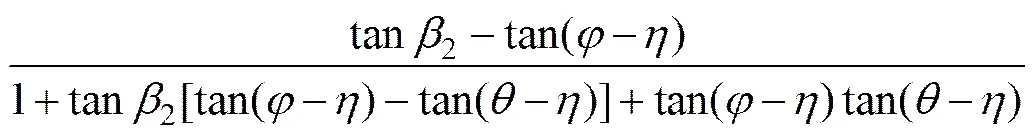
令2为隧道左侧侧压力系数，则

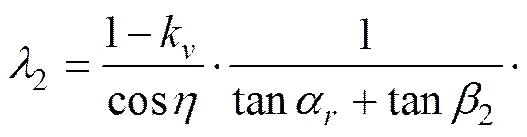
(20)

为使T取得极大值，令，可得

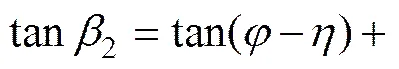
式中：为面的计算摩擦角；为面的摩擦角，且＜。由文献[13]可知：可由确定，2可由，和α确定。据文献[13]，隧道右侧水平向侧压力为

2.4 拱顶围岩竖向压力

由于与相比，与相比，其所占比重往往均较小，而且衬砌与土之间的摩擦角也不同，据文献[13]，将隧道拱顶上覆岩土体考虑为部分。为便于分析计算，将产生竖向位移的覆盖岩土体分为2部分即和(如图1所示)分别进行讨论。

对于岩土体，地震动作用下所受荷载及各参数如图6所示。其中，l为隧道拱顶部分对岩土体总的反力，其大小等于岩土体对隧道拱顶的总垂直压力；3为岩土体的重力。

由几何关系可知

将式(13)，(21)，(24)代入式(25)得

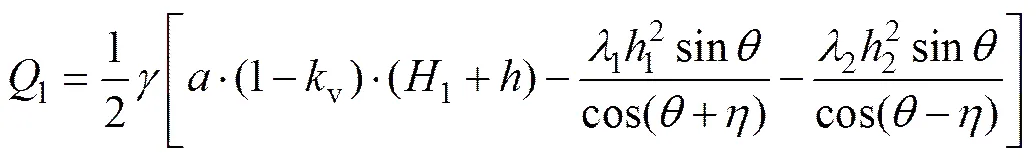
将Q换算为作用在后行洞拱顶支护结构上的均布荷载为

(28)

设岩土体作用于隧道洞顶部的垂直压力FH为1，侧为2，为的长度，据文献[13]，左、右侧之间按线性变化，则

对于岩土体，地震动作用下所受荷载及各参数如图7所示。r为隧道拱顶部分对岩土体总的反力，其值等于岩土体对隧道拱顶的总垂直压力。4为岩土体的重力。

图7 地震力作用下拱顶岩土体EIJG受力计算简图

同理可得

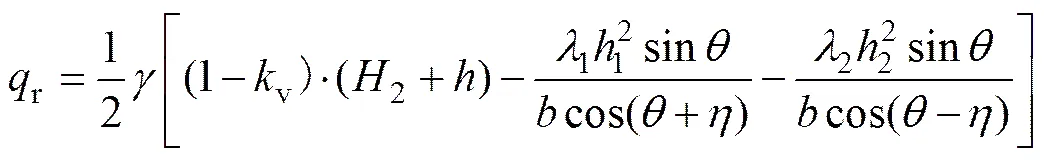
设岩土体作用于隧道洞顶部的垂直压力为3，侧为4，的长度为。根据文献[13]，左右侧之间按线性变化，则

出于安全考虑，处取q和q中的较大值。根据上述理论推导可得地震荷载作用下浅埋双侧偏压隧道松动围岩围岩压力分布，如图 8所示。

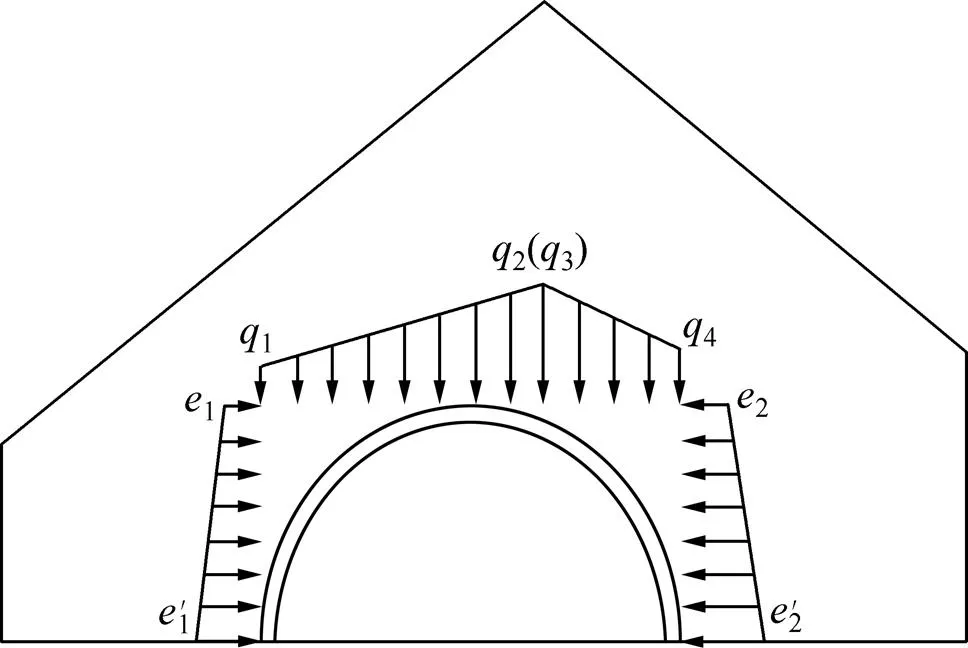
图8 地震力作用下双侧偏压隧道围岩压力分布图

3 对比验证

水平和竖向地震力同时作用下浅埋双侧偏压隧道结构荷载计算模型的建立是为了便于这种隧道的抗震设计计算而建立的一种简化计算模型。通过推导得到的计算式需要进一步验证。

在不考虑地震力荷载作用时，此时地震力偏角0时。则式(12)和(20)可化简为：

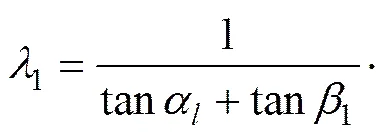
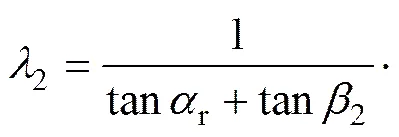
通过对比分析可知，式(32)和(33)与文献[15]中式(1)和(10) 是完全一致的，可知本文所选用的分析思路是可行的，所建立的水平和竖向地震力同时作用下浅埋双侧偏压隧道结构荷载计算模型是合理的。文献[15]中所分析建立的浅埋双侧偏压隧道松动围岩压力计算模型在某种程度上是本文所建模型的一种特例，即地震力荷载为0时的情况。

4 参数分析

4.1 围岩级别对双侧偏压隧道破裂角的影响

根据文献[7]，选取不同围岩条件(见表1)。考虑地震烈度为VII度，取h=0.1，v=0.05，根据式(5)可得6.00°。取l45°，r60°。根据式(14)和式(22)，可得到不同围岩级别时破裂角1和2(见表1)。

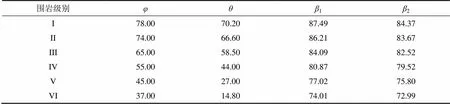
表1 围岩参数及破裂角计算值

注：在实际工程中，隧道浅埋地段部分围岩几乎不存在，为凸显变化规律，将全部级别围岩考虑在内。

由表1可知：在考虑水平和竖向地震荷载共同作用时，随着围岩级别从I级到VI级逐级提高，双侧浅埋偏压隧道左侧的破裂角从87.49°逐渐减小至74.01°，双侧浅埋偏压隧道右侧的破裂角从84.37°逐渐减小至72.99°。隧道两侧的破裂角的变化随围岩级别变化的趋势相同，围岩级别越高，破裂角越小。

4.2 地面坡度对双侧偏压隧道破裂角的影响

选取级别为V级和VI级围岩的隧道分别进行分析。考虑地震烈度为Ⅵ，Ⅶ，Ⅷ和Ⅸ度，相应的水平地震加速度系数h则分别为0.05，0.10，0.20 和0.40，取v=0.5h。根据式(5)，可得地震力偏角分别为2.93°，6.00°,12.53°，26.57°。根据式(14)和式(22)，可得到隧道围岩为V级和VI级时不同地面坡度时的破裂角1和2，见表2~5。

由表2~5可知：对于同一围岩级别的浅埋双侧偏压隧道，当地震烈度相同时，隧道左、右两侧破裂角随地面坡度变化的趋势相同，地面坡度的角度越大，其对应一侧的破裂角越大。从表2和表3可知：对于围岩级别为V级的隧道，当地震烈度为Ⅵ度，隧道左侧地面坡度为15°时，1最小，为74.09°；而当隧道左侧地面坡度增为60°时，隧道左侧的破裂角随之增大，最大值为77.62°；隧道右侧的破裂角变化与隧道左侧的相同，在地面坡度分别为15°，30°，45°和60°时，2从71.91°依次增加为73.29°，74.70°，76.43°；当浅埋双侧偏压隧道两侧的地面坡度相同时，隧道左侧的破裂角要大于隧道右侧的破裂角。

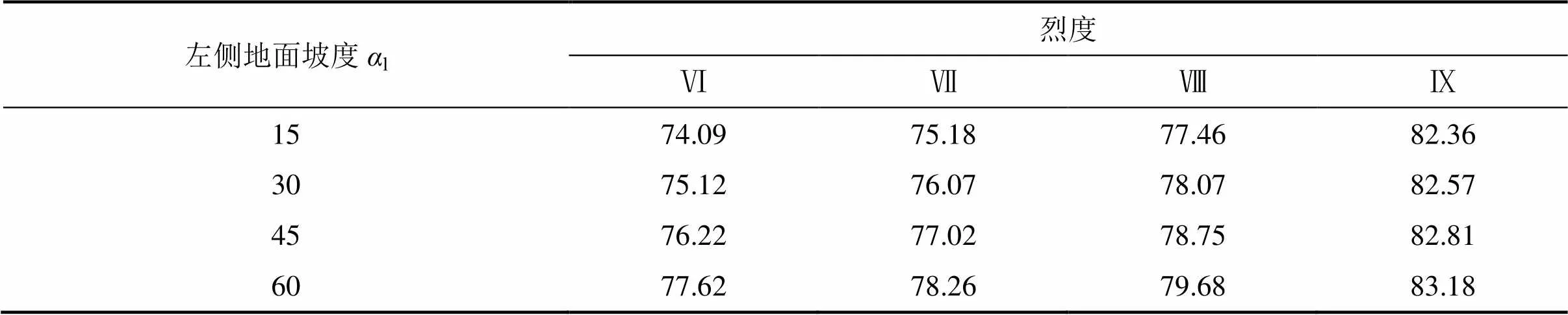
表2 左侧地面坡度下破裂角计算值β1(V级围岩)

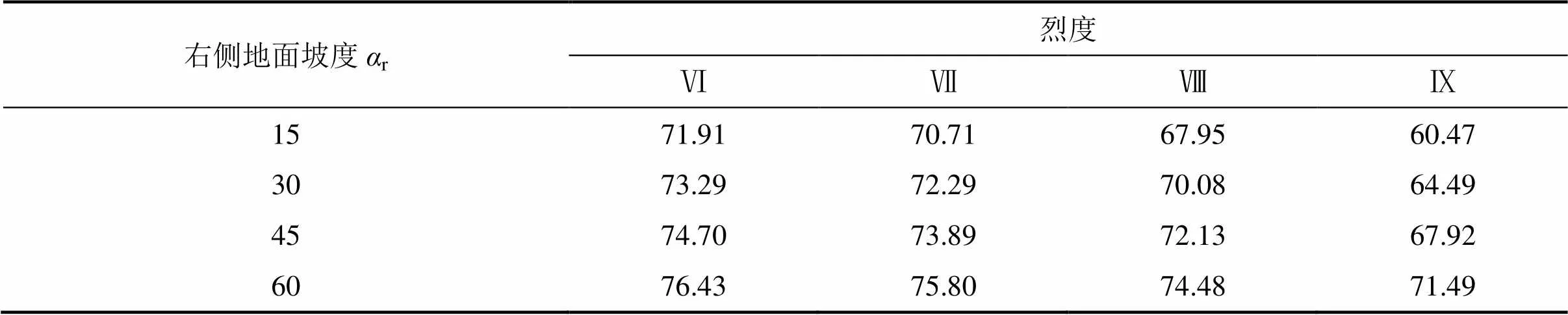
表3 右侧地面坡度下破裂角计算值β2(V级围岩)

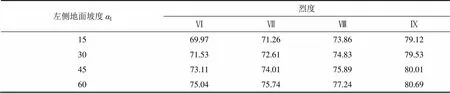
表4 左侧地面坡度下破裂角计算值β1(VI级围岩)

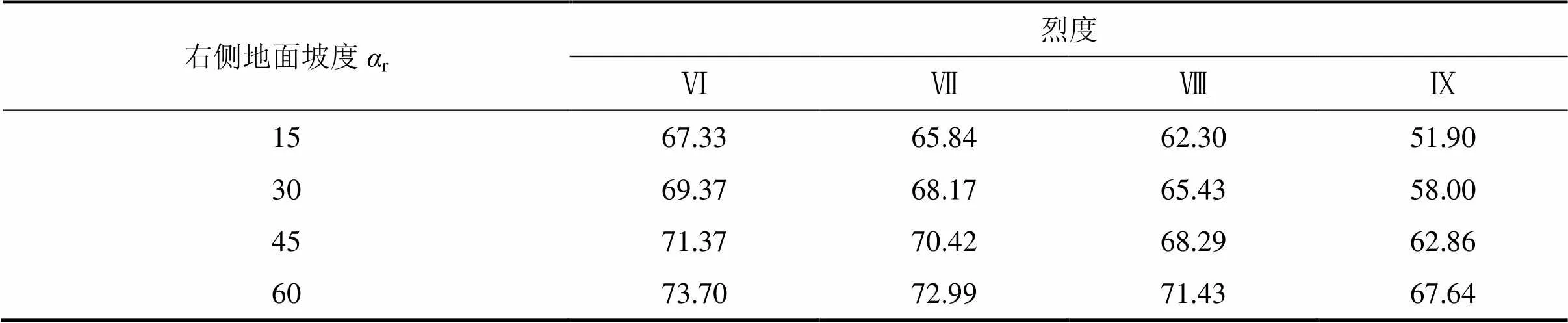
表5 右侧地面坡度下破裂角计算值(VI级围岩)

对于V级围岩隧道，当地震烈度为Ⅵ，Ⅶ，Ⅷ，Ⅸ度时，其破裂角的变化范围分别为71°~78°，70°~79°，67°~80°和60°~84°。对于Ⅵ级围岩隧道，当地震烈度Ⅵ，Ⅶ，Ⅷ，Ⅸ度时，其破裂角的变化范围分别为67°~76°，65°~76°，62°~78°和51°~81°。

4.3 地震烈度对双侧偏压隧道破裂角的影响

由表2和表3可知：对于浅埋双侧偏压隧道左侧，当l一定时，随着地震烈度增加，破裂角随之增加。例如，取l=45°，当地震烈度分别Ⅵ，Ⅶ，Ⅷ，Ⅸ度时，隧道左侧的破裂角分别为76.22°，77.02°，78.75°和82.81°。

而对于浅埋双侧偏压隧道右侧，其变化趋势则与左侧的不同。当r一定时，随着地震烈度增加，破裂角随之减小。例如，取r=60°，在地震烈度为Ⅵ度时，隧道右侧的破裂角最大，为76.43°；随着地震烈度增加，r一次递减为75.74°，77.24°和80.69°。

从表4和表5也可得出上述规律。

根据以上规律可知：浅埋双侧偏压隧道两侧的破裂角随地震烈度增加，其变化趋势完全相反，易知上述分析是在水平地震荷载方向向左的基础上进行的。若水平地震荷载的方向向右，则此时地震力偏角在各计算式中要添加个负号，同时，浅埋双侧偏压隧道左右两侧破裂角随地震烈度增加而变化的趋势与表2~5所示的相反。

综上可知：在地面坡度和围岩级别相同时，隧道两侧破裂角随地震烈度增加的变化趋势完全相反，一侧增加，另一侧递减，可结合水平地震力的方向进行判断，或者根据地震力偏角的方向进行判断。

5 结论

1) 从理论推导可知，隧道两侧的破裂角是地面坡度角、岩土体的计算摩擦角和地震力偏角的函数，可由，和确定。

2) 当地震烈度和地面坡度相同时，随着围岩级别从I级到VI级逐级提高，隧道两侧的破裂角逐渐减小。当地震烈度和围岩级别相同时，随着地面坡度逐渐增大，隧道两侧的破裂角也逐渐增大。

3) 对于地面坡度为15°~60°的浅埋双侧偏压隧道，当隧道围岩级别为V级时，针对抗震设防烈度依次为Ⅵ，Ⅶ，Ⅷ和Ⅸ度的隧道，建议对其两侧地表进行加固的破裂角范围分别为68°~81°，67°~82°，64°~83°和57°~87°；当隧道围岩级别为Ⅵ级时，针对抗震设防烈度依次为Ⅵ，Ⅶ，Ⅷ和Ⅸ度的隧道，建议对其两侧地表进行加固的破裂角范围分别为64°~79°，62°~79°，59°~81°和48°~84°。

4) 在地面坡度和围岩级别相同时，若水平地震力方向或地震力偏角方向向左，则随着地震烈度增加，隧道左侧的破裂角越来越大，右侧的破裂角越来越小；若水平地震力方向或地震力偏角方向向右，则随着地震烈度的增加，隧道左侧的破裂角越来越小，右侧的破裂角越来越大。

以上破裂角的变化规律可为地震作用下浅埋双侧偏压隧道地表加固范围的确定提供参考。

参考文献：

[1] SARI Y D, PASAMEHMETOGLU A G, CETINER E, et al. Numerical analysis of a tunnel support design in conjunction with empirical methods[J]. International Journal of Geomechanics, 2008, 8(1): 74−81.

[2] SHAO Y, MACARI E J. Information feedback analysis in deep excavations[J]. International Journal of Geomechanics, 2008, 8(1): 91−103.

[3] 雷明锋, 彭立敏, 施成华, 等. 浅埋偏压隧道衬砌受力特征及破坏机制试验研究[J]. 中南大学学报(自然科学版), 2013, 44(8): 3316−3325. LEI Mingfeng, PENG Limin, SHI Chenghua, et al. Model research on failure mechanism and lining stress characteristics of shallow buried tunnel under unsymmetrical pressure[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3316−3325.

[4] 唐明明, 王芝银, 李云鹏. 穿越公路偏压小净距隧道施工方法探讨[J]. 岩土力学, 2011, 32(4): 1163−1168. TANG Mingming, WANG Zhiyin, LI Yunpeng. Study of construction methods for crossing bias small interval highway tunnel[J]. Rock and Soil Mechanics, 2011, 32(4): 1163−1168.

[5] 刘新荣, 郭子红, 谢应坤, 等. 不良地质下偏压隧道支护结构开裂与治理分析[J]. 工程勘察, 2010(5): 1−5. LIU Xinrong, GUO Zihong, XIE Yingkun, et al. Analysis on the cracking and the treatment of support structure for asymmetrically loaded tunnel in unfavorable geological conditions[J]. Geotechnical Investigation and Surveying, 2010(5): 1−5.

[6] 来弘鹏, 杨万精, 谢永利. 软岩大变形偏压公路隧道变形与荷载作用特征[J]. 中南大学学报(自然科学版), 2014, 45(6): 1924−1931. LAI Hongpeng, YANG Wanjiang, XIE Yongli. Analysis on deformation and load action features of large-deformation bias highway tunnel in soft rock[J]. Journal of Central South University (Science and Technology), 2014, 45(6): 1924−1931.

[7] SANCHEZ-MERINO A L, FERNANDEZ-SAEZ J, NAVARRO C. Simplified longitudinal seismic response of tunnels linings subjected to surface waves[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(3): 579−582.

[8] 蒋树屏, 方林, 林志. 不同埋置深度的山岭隧道地震响应分析[J]. 岩土力学, 2014, 35(1): 211−217. JIANG Shuping, FANG Lin, LIN Zhi. Seismic response analysis of mountain tunnels in different depths[J]. Rock Soil Mechanics, 2014, 35(1): 211−217.

[9] 徐华, 李天斌, 王栋, 等. 山岭隧道地震动力响应规律的三维振动台模型试验研究[J]. 岩石力学与工程学报, 2013, 32(9): 1762−1761. XU Hua, LI Tianbin, WANG Dong, et al. Study of seismic responses of mountain tunnels with 3D shaking table model test[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1762−1761.

[10] JTJ 004—89, 公路工程抗震设计规范[S]. JTJ 004—89, Specification of earthquake resistant design for highway engineering[S].

[11] 黄帅, 宋波, 蔡德钩, 等. 近远场地震下高陡边坡的动力响应及永久位移分析[J]. 岩土工程学报, 2013, 35(S2): 768−773. HUANG Shuai, SONG Bo, CAI Degou, et al. Dynamic response and permanent displacement of high-steep slopes under near- and far-field earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 768−773.

[12] 袁勇, 禹海涛, 陈之毅. 软土浅埋框架结构抗震计算方法评价[J]. 振动与冲击, 2009, 28(8): 50−56. YUAN Yong, YU Haitao, CHEN Zhiyi. Evaluation of seismic calculation methods for shallow-buried frame structures in soft-soil[J]. Journal of Vibration and Shock, 2009, 28(8): 50−56.

[13] JTG D70—2004, 公路隧道设计规范[S]. JTG D70—2004, Code for design of road tunnel[S].

[14] 谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011: 1−50. XIE Dingyi. Soil dynamics[M]. Beijing: Higher Education Press, 2011: 1−50.

[15] 钟祖良, 涂义亮, 刘新荣, 等. 浅埋双侧偏压小净距隧道衬砌荷载及其参数敏感性分析[J]. 土木工程学报, 2013, 46(1): 119−125. ZHONG Zuliang, TU Yiliang, LIU Xinrong, et al. Calculation of lining load of shallow-buried bilateral bias twin tunnel and its parameter sensitivity analysis[J]. China Civil Engineering Journal, 2013, 46(1): 119−125.

(编辑 陈灿华)

Loosening earth pressure of shallow bilateral bias tunnel under earthquake force

LI Dongliang, LIU Xinrong, YANG Xin, WANG Zhen, YUAN Wen

(Key Laboratory of New Technology for Construction of Cities in Mountain Area,School of Civil Engineering, Chongqing University, Chongqing 400045, China)

To explore the distribution law of loosening earth pressure of shallow bilateral bias tunnel with the horizontal and the vertical seismic force, the analytical solutions of loosening earth pressure of shallow bilateral bias tunnel were derived by pseudo-static method. Based on the derived formula, the changing rules of the crack angle on the both sides of the tunnel were researched. The results show that the crack angle of the shallow bilateral buried tunnel decreases with the increase of the surrounding rock grade. But the higher the land slope, the larger the break angle of the shallow bilateral buried tunnel. With the increase of the earthquake intensity, one crack angle decreases, but the other increases, which should be judged by the direction of horizontal seismic force or deflection angle of the earthquake force. As for the tunnel of which the surrounding rock is poor, such as V and VI class surrounding rock, the suggestions about reinforce range of the crack angle are given according to the different seismic fortification intensities(VI,Ⅶ,Ⅷ and Ⅸ).

pseudo-static method; earthquake force; bilateral bias tunnel; crack angle; loosening earth pressure

10.11817/j.issn.1672-7207.2016.10.027

U455

A

1672−7207(2016)10−3483−08

2015−10−22；

2015−12−26

国家自然科学基金资助项目(41372356)；教育部“新世纪优秀人才支持计划”项目(NCET-05-0763)(Project(41372356) supported by the Key Project of National Natural Science Foundation of China; Project(NCET-05-0763) supported by the “Program for New Century Excellent Talents in University” of Ministry of Education)

刘新荣，教授，从事岩石力学、边坡、隧道与地下空间工程等研究；E-mail：liuxrong@126.com