电磁力减振过渡过程的机理研究

张辉，范宝春，刘梦珂

（南京理工大学瞬态物理国家重点实验室，江苏南京210094）

电磁力减振过渡过程的机理研究

张辉，范宝春，刘梦珂

（南京理工大学瞬态物理国家重点实验室，江苏南京210094）

电介质溶液中，电磁场产生的电磁力可以控制流体的运动。将其用于钝体绕流时，可以抑制分离和消除涡街，从而达到减振的目的。为了研究电磁力减振的过渡过程，将指数极坐标系建立在运动的圆柱上，推导了运动坐标中，基于涡生振荡并考虑电磁力的涡量-流函数守恒方程及其初始和边界条件，圆柱表面的水动力表达式以及圆柱振荡方程。对圆柱从静止开始振荡，到发展为稳定振荡状态，然后又在电磁力作用下衰减，直至成为新的稳定态发展过程进行了计算和讨论，描述了圆柱振荡、脱体涡街和能量传递的发展过程，以及升阻力相图的连续变形和漂移。结果表明：圆柱振动的诱因在于流动分离产生的尾涡诱导的升力周期变化；圆柱表面附近分布的切向电磁力可以有效改变边界层附近流体的流动，抑制流动分离，从而使流场趋于对称，消除升力的周期振动，最终抑制圆柱的振动甚至在电磁力较大时可以消除振动。

兵器科学与技术；流体控制；涡生振荡；电磁力；减振

0 引言

黏性流体在运动物体表面形成的边界层可使该物体减速，产生振动甚至失稳［1］，这往往不是人们所期望的，而这些现象通常可以通过流体边界层的控制加以抑制。动力推进的物体，通过对其表面边界层的有效控制，可以提高推进效率、增加运动的稳定性、减少意外的变形和损坏，这些对改进飞机、舰船、导弹或普通弹箭的性能是非常有价值的。

长期以来，人们发现许多控制边界层流动的方法，其中有些不需向流场提供能量，称作被动控制，如加置肋条、带狭缝的板和二次圆柱等。有些则需要向流场添加能量，称作主动控制，如振荡和旋转圆柱，声波干扰、表面狭缝吹吸和热效应等。对于主动控制，向流场提供能量可以根据流场信息来调整，即可以进行反馈式控制，这种控制方式更具实用价值。利用电磁场控制边界层流动是一种主动控制方法，它可以灵活改变电磁力的方向，实现反馈式控制，甚至制成微机电系统（MFMS），因此受到广泛关注［2］。早在20世纪中叶，人们就设想用电磁力控制电解质溶液的流动。Gai1itis等［3］设计了一种由电极和磁极交错布置的电磁场激活板，将其浸入流动的弱电解质时，激活板附近形成的洛伦兹力可以改变流体边界层结构。Weier等［4］将此类激活板包覆在圆柱两侧，对由此形成的圆柱绕流进行了实验研究，实现了电磁力对圆柱绕流流场的控制。Crawford等［5］则从理论上讨论了激活板的电磁场和洛伦兹力分布。Kim等［6］、Posdziech等［7］发现常电磁力和脉冲电磁力对抑制升力、稳定流场都有一定的效果。国内上海交通大学尤云祥教授课题组［8］对固定圆柱的电磁激活板宽度对流场控制效果的影响进行了数值研究。另外，Zhang等曾对圆柱的涡生振荡进行了数值研究［9］，对电磁力减振过程已做过相关的实验研究［10-11］，而对于深层次的电磁控制机理和动态过程仍需相关的数值研究去揭示。

本文将坐标系建立在运动的圆柱上，推导了运动坐标中，考虑电磁力涡生振荡的涡量-流函数守恒方程及其初始和边界条件，圆柱表面的水动力表达式以及圆柱振荡方程。对圆柱从静止至开始振荡，到发展为稳定振荡状态，然后又在电磁力作用下衰减，直至成为新的稳定态整个发展过程进行了计算和讨论，描述了圆柱振荡、脱体涡街和能量传递的发展过程，以及升阻力相图的连续变形和漂移。

1 守恒方程

将圆柱置入均匀流动的流体中，当雷诺数大于某值时，由于涡在圆柱表面的周期性脱落，导致其表面的水动力周期变化。若圆柱被固定在柔性支架上，在周期变化的力作用下，圆柱将周期性的振动，称为涡生振荡（VIV）。振荡的圆柱又会影响圆柱周围流体的流动，进而改变圆柱表面的水动力，从而改变圆柱的运动，如此反复。因此，这是一个标准的流体-固体耦合问题。

为了控制涡生振荡，对置入弱电解质溶液中的圆柱表面包覆由电极条和磁极条相间排列的电磁激活板，如图1所示。圆柱表面附近将形成电磁力场，由右手定则可知，电磁力的方向与流体流动方向一致。流体在电磁力的作用下加速，边界层的结构因此而改变。

图1　电磁控制涡生振荡原理图Fig.1 Princip1e scheme of VIV contro11ed by Lorentz force

对于二维情况，电磁力沿轴向平均后，洛伦兹力F的无量纲形式［4，7］可以表示为

有

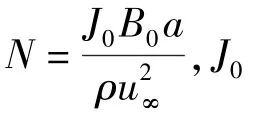
将坐标系建立在振动圆柱上。对于不可压缩的二维流动，在指数极坐标（ξ，η）下（r=e2πξ，θ= 2πη），考虑电磁力的无量纲形式，涡量流函数方程为

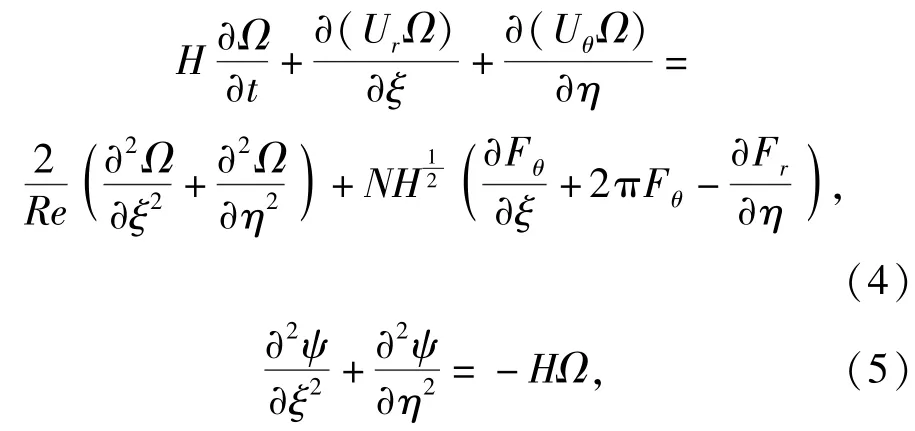
若圆柱仅沿横向（垂直于流向）振动，则初始条件和边界条件［9］为

2 圆柱表面水动力

2.1剪应力与压力

圆柱受到流体的力Fθ*，由剪应力和压力两部分组成，即

式中

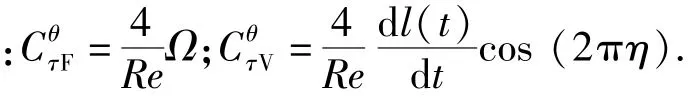
显然，电磁力通过改变流场和圆柱的运动状态来改变圆柱表面的剪应力，但并未直接出现在剪应力方程中。

式中：pθ为圆柱表面角度为θ处的压力；p∞为无穷远处的压力。

因为电磁力仅存在切向分量，故运动坐标系下的动量方程为

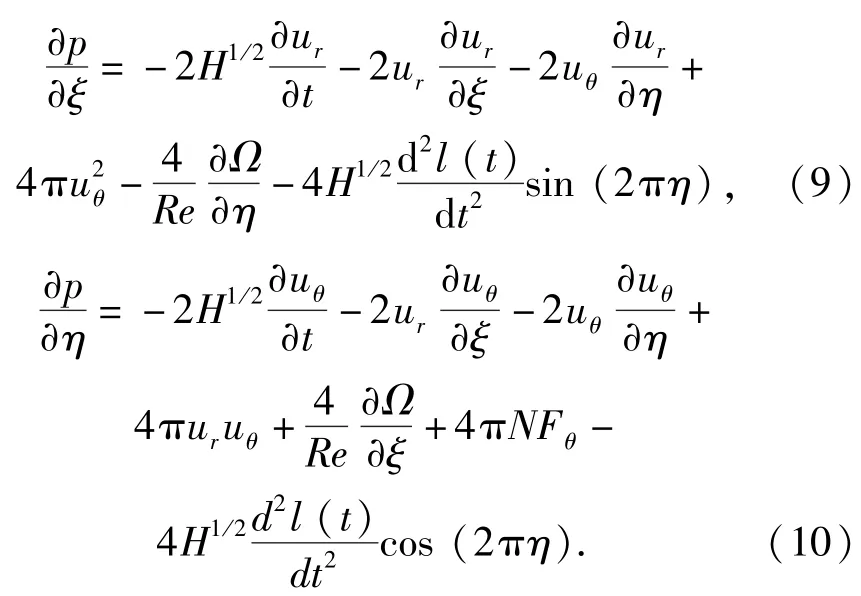
在圆柱表面

沿着η方向从η=0到η对（12）式积分，可得

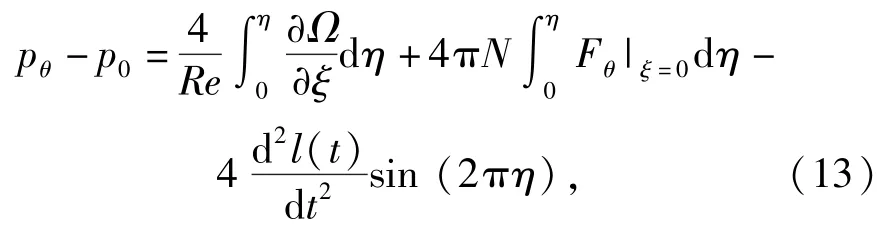
沿着ξ方向（η=0）从ξ=0到∞对（9）式积分，可得

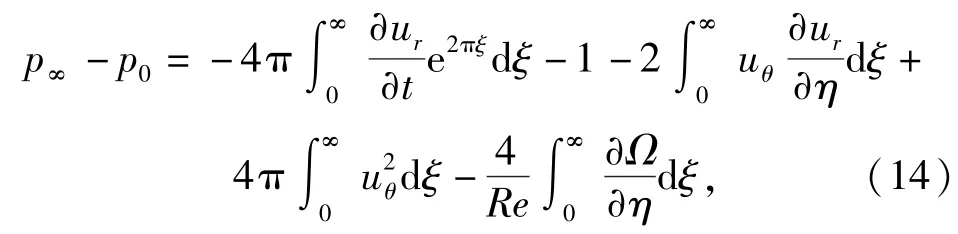
因此

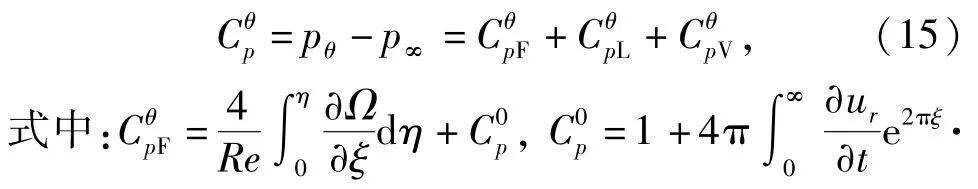
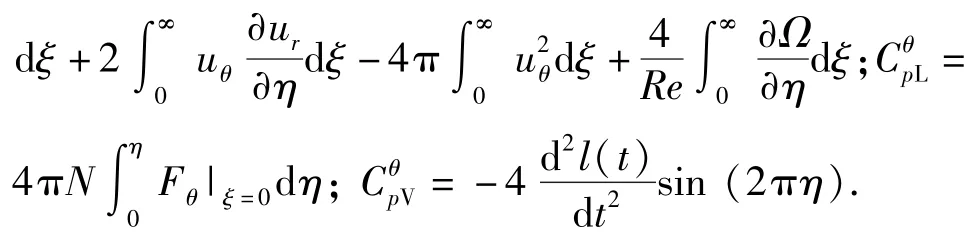
2.2阻力和升力

阻力分布函数

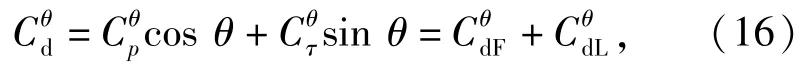
式中：下脚标dF表示涡生阻力，该值受到场电磁力的影响；dL表示壁电磁力诱导的阻力（电磁推力），此值仅与壁面电磁力有关，而与流动无关。

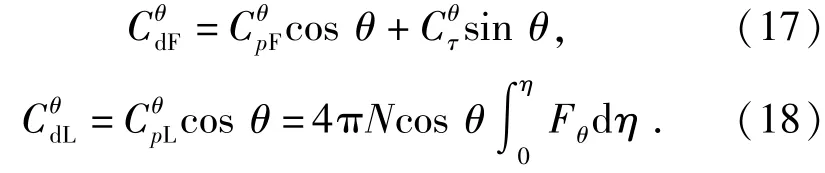
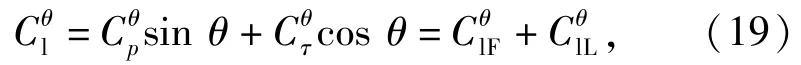
式中：下脚标1F表示涡生的升力；1L表示壁面电磁力诱导的升力，此值与流动无关。

总阻力Cd为

总升力C为

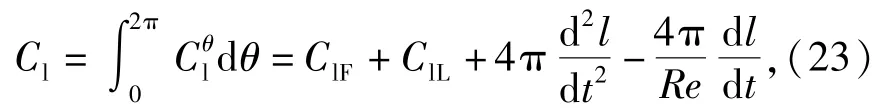
显然，（23）式中作用于圆柱的升力由4部分组成，其中，方程右侧第1项C1F为涡生力，与圆柱表面的涡量和涡通量有关，该值受场电磁力的影响；第2项C1L为电磁升力，此值仅与壁面电磁力有关，而与流动无关，电磁力对称分布时C1L=0；第3项为惯性力，与圆柱的加速度有关；第4项为粘性阻尼力Cdamp，与雷诺数和圆柱的运动速度有关。第2项、第3项和第4项均与流场的变化无关。

2.3圆柱运动方程

无量纲的圆柱运动方程

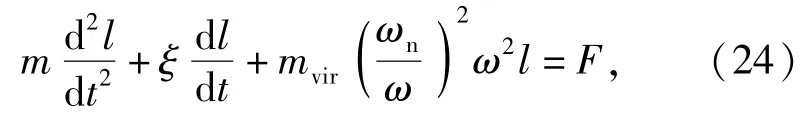
每个周期内能量传递的无量纲形式为

数值计算时，动量方程（4）式采用交替方向隐式格式，流函数方程（5）式采用快速傅里叶变换格式，圆柱运动方程（25）式采用Runge-Kutta法［9］。计算空间步长Δξ=0.004，Δη=0.002，时间Δt=0.005.

3 结果与讨论

涡的周期脱落产生振荡升力，从而使静止圆柱在升力的作用下逐渐发展为稳定振荡的圆柱，在电磁力加载后，边界层流体的动量增大，抑制圆柱两侧流体的分离和脱体，减小脱体导致的升力振荡，流场和圆柱又经历一段非定常的发展过程，最终会达到新的稳定状态。

图2为圆柱从固定至稳定振荡，再经电磁力作用，趋于新的稳定过程的位移随时间变化曲线。在t1=446时刻，解除横向约束，圆柱开始振荡，振幅逐渐增大。在t=620时刻，达到稳定状态，振幅不再变化。在t2=650时刻，加载电磁力。电磁力作用下，圆柱振荡逐渐衰减（图2中实线和虚线分别对应电磁力作用参数N=0.8和N=3.0）。若电磁力足够大（N=3.0），圆柱会趋于静止，不再振荡。

当振荡圆柱远离平衡位置时，升力C1F（t）做功为正，即流体对圆柱做功，增加圆柱的能量，反之亦然。另外，阻尼力Cdamp做功始终为负，即减少圆柱的能量。图3所示（与图2对应）从静止圆柱到稳定振荡再到电磁力作用下趋于新的稳定振荡全过程中，流体-固体间的能量传递变化，其中图3（a）、图3（b）分别对应电磁力作用参数N=0.8和N= 3.0.虚线表示升力C1F（t）做功E1，点划线表示阻尼力Cdamp做功Ed，实线表示每个周期转移的总能量E，是E1与Ed之和。

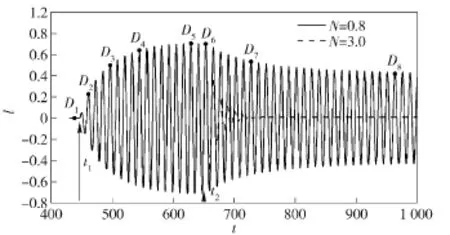
图2　涡生振荡发展和电磁力抑制过程中圆柱的位移变化Fig.2 Disp1acement variation of cy1inder over time in the process of VIV evo1ution and suppression by Lorentz force

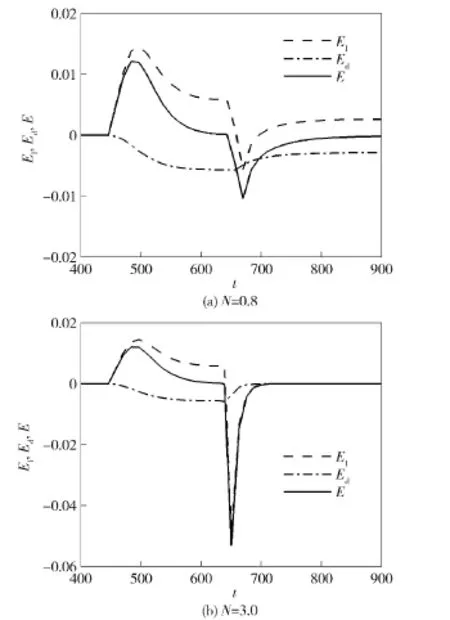
图3　涡生振荡发展和电磁力抑制过程中的能量变化Fig.3 Variation of transferred energy for VIV evo1ution and suppression by Lorentz force

圆柱刚开始振荡时，E1的绝对值大于Ed，因此升力做的正功占主导。随着圆柱的振幅逐渐增大，E1的绝对值先增大后减小，而Ed的绝对值单调增大至与E1的绝对值相等，此时二者之和，即E为0.因此，圆柱达到稳定振动状态。t=650时加载电磁力，E1迅速减小，以致有一段时间为负值。能量从圆柱传递给流体，圆柱振荡衰减。最终总能量E=0，此时E1为正，Ed为负，圆柱以较小振幅稳定振荡，如图3（a）所示（N=0.8）。当电磁力足够大（N=3.0）时，圆柱最终不再振荡，此时E1=Ed=0，如图3（b）所示。

圆柱从固定至稳定振荡的发展过程中，流场涡量变化如图4所示，其中红色表示正涡，蓝色表示负涡，“+”表示圆柱从固定释放的初始0位。图4中的时刻Di与图2相对应，即圆柱的位置处于上侧最大位移处。在t1=446时刻，圆柱的横向约束被解除，在升力作用下开始振荡。由于能量从流体转移到圆柱，因此圆柱的振幅增大，对应的流场如图4中的D1～D4.当总能量达到平衡时，圆柱的振荡也达到稳定，此时流场对应D5，计算结果与文献［10］中实验结果一致。

电磁力控制过程中，振荡圆柱的绕流变化如图5所示。时刻Di与图2相同，对应于圆柱处于上侧最大位移。D5时刻，圆柱的涡生振荡已经稳定。此后，在t2=650时刻加载电磁力，边界层的流体在电磁力的作用下加速，流动分离得到抑制，圆柱上下两侧分离点的距离减小，尾流涡被拉长，涡距沿流向变大，而沿横向变小，如图5（a）～图5（c）所示。电磁力足够大时，分离点消失，流场对称且定常，如图5（d）～图5（f）所示，计算结果与文献［10］中实验结果一致。

流场的变化导致升阻力的变化。涡生振荡发展和电磁力控制过程中，振荡圆柱的涡生升阻力CdF-C1F相图的发展变化如图 6所示。A1B1C1D1A1对应固定圆柱的升阻力相图，由于圆柱振荡对圆柱上下两侧剪切层的作用，使相图逐渐发生180°的反转。随着圆柱振荡的加剧，圆柱的能量增大，点A 与C分离，打破了曲线的镜像对称。另外，阻力平均值以及阻力和升力的振幅增大，导致曲线从左向右不断延伸，直至振荡达到稳定，A与C再次重合，即对应相图A5B5C5D5A5.电磁力作用下，尽管总阻力Cd减小，但涡生阻力CdF是增大的。因此，加载电磁力后，曲线显著向右移动。由于电磁力对流动分离的抑制，并使流场趋于对称，故升力C1F减小，曲线逐渐萎缩，从而使圆柱的振荡减弱，并最终以较小的振幅稳定振荡，对应图 6（a）中的闭合曲线A8B8C8D8A8，此时A点与C点也再次重合。N=3.0时，电磁力能够完全抑制流动分离，使绕流流场完全对称，此时相图曲线逐渐萎缩成升力为0的点（A8B8C8D8A8）.

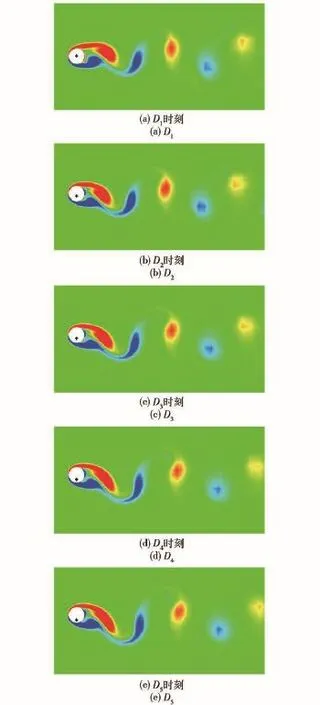
图4　振动发展过程中流场涡量的变化Fig.4 Variation of vorticity in f1ow fie1d during VIV evo1ution

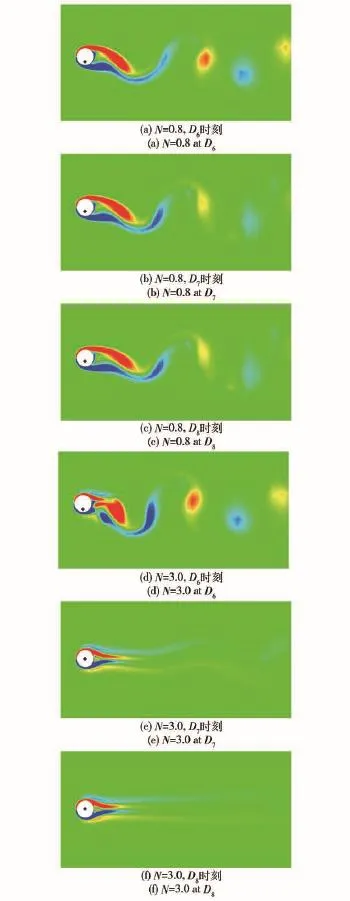
图5　电磁力抑制过程中振荡圆柱的流场涡量变化Fig.5 Variation of vorticity in f1ow fie1d during suppression by Lorentz force

电磁力的作用下，涡生振荡得到抑制，最终以较小振幅稳定振荡，控制后的振幅大小与电磁力的强度有关。图7为控制后的振幅随电磁力强度的变化图。圆柱振幅随N的增大而减小，当N足够大时，振荡被完全抑制，圆柱静止（图7中虚线表示电磁力的临界值，介于2.5到3.0之间）。

图6　涡生振荡发展和电磁力抑制过程的升阻力相图Fig.6 Lift-drag phase diagram for VIV deve1opment and suppression by Lorentz force

图7　圆柱的振幅随电磁力强度（作用参数N）的变化Fig.7 VIV amp1itude versus interaction parameter N

4 结论

本文将坐标系建立在运动的圆柱上，推导了运动坐标中，考虑电磁力涡生振荡的涡量-流函数守恒方程及其初始和边界条件，圆柱表面的水动力表达式以及圆柱振荡方程。对圆柱从静止开始振荡，到发展为稳定振荡状态，然后又在电磁力作用下衰减，直至成为新的稳定态发展过程进行了计算和讨论。结果表明，圆柱振动的诱因在于尾涡诱导的升力周期变化，而圆柱表面附近分布的切向电磁力可以有效改变边界层附近流体的流动，抑制流动分离，从而使流场趋于对称，消除升力的周期振动，最终抑制圆柱的振动。

（References）

［2］Tu J H，Zhou D，Bao Y，et a1.F1ow-induced vibrations of two circu1ar cy1inders in tandem with shear f1ow at 1ow Reyno1ds number［J］.Journa1 of F1uids and Structures，2015，59：224-251.

［2］Reddy P D S，Bandyopadhyay D，Joo S W，et a1.Parametric study on instabi1ities in a two-1ayer e1ectromagnetohydrodynamic channe1 f1ow confined between two para11e1 e1ectrodes［J］.Physica1 Review F，2011，83（3）：036313.

［3］Gai1itis A，Lie1ausis O.On a possibi1ity to reduce the hydrodynamica1 resistance of a p1ate in a e1ectro1yte［J］.App1ied Magnetohydrodynamics，1961，12：143-146.

［4］Weier T，Gerbeth G，Posdziedch O，et a1.Fxperiments on cy1inder wake stabi1ization in an e1ectro1yte so1ution by means of e1ectromagnetic forces 1oca1ized on cy1inder surface［J］.Fxperimenta1 Therma1 and F1uid Science，1998，16（1）：84-91.

［5］Crawford C，Karniadakis G F.Reyno1ds stress ana1ysis of FMHD-contro11ed wa11 turbu1ence［J］.Physics of F1uids，1997，9（3）：788-806.

［6］Kim S，Lee C M.Contro1 of f1ows around a circu1ar cy1inder：suppression of osci11atory 1ift force［J］.F1uid Dynamics Research，2001，29（1）：47-63.

［7］Posdziech O，Grundmann R.F1ectromagnetic contro1 of seawater f1ow around circu1ar cy1inders［J］.Furopean Journa1 of Mechanics-B/F1uids，2001，20（2）：255-274.

［8］尹纪富，尤云祥，胡天群，等.电磁极宽度对圆柱绕流场影响的数值分析［J］.力学学报，2013，45（4）：493-506. YIN Ji-fu，YOU Yun-xiang，HU Tian-qun，et a1.Numerica1 ana1-ysis for the effect of the e1ectromagnetic actuator width on f1ow structures around a circu1ar cy1inder［J］.Chinese Journa1 of Theoretica1 and App1ied Mechanics，2013，45（4）：493-506.（in Chinese）

［9］Zhang H，Fan B C，Chen Z H，et a1.An in-depth study on vortex-induced vibration of a circu1ar cy1inder with shear f1ow［J］. Computers and F1uids，2014，100（1）：30-44.

［10］Zhang H，Fan B C，Chen Z H，et a1.Fxperimenta1 investigations on the mechanism of 1ift amp1ification and osci11atory suppression of Lorentz force［J］.Defence Techno1ogy，2013，9（2）：110-116.

［11］Zhang H，Fan B C，Li H Z.Lift enhancement and osci11atory suppression of vortex-induced vibration in shear f1ow by Lorentz force［J］.Journa1 of China Ordnance，2012，8（3）：139-145.

Mechanism Investigation on Transient Process of Oscillatory Suppression by Lorentz Force

ZHANG Hui，FAN Bao-chun，LIU Meng-ke
（Nation Key Laboratory of Transient Physics，Nanjing University of Science and Techno1ogy，Nanjing 210094，Jiangsu，China）

The f1ow of weak e1ectro1yte so1ution can be contro11ed by Lorentz force generated by the suitab1y-chosen e1ectromagnetic fie1d.Lorentz force can be used to suppress the vortex shedding and e1iminate the vortex street in the f1ow around a b1uff body for the suppression of vortex-induced vibration （VIV）.To investigate the evo1utions of VIV suppression by Lorentz force，an exponentia1 po1ar coordinate system is set up on a moving cy1inder，and the stream function-vorticity equations considering the Lorentz force and its initia1/boundary conditions，an expression of hydrodynamic force on the cy1inder surface as we11 as the cy1inder response equations are then derived.The who1e evo1utions of cy1inder from resting and then undergoing deve1opment and suppression due to Lorentz force are ca1cu1ated and discussed.The deve1opment process of cy1inder vibration，vortexes shedding and energy transfer，and the deformation and shift of drag-1ift phase diagram are described.The resu1ts show that the reason of cy1inder osci11ation is the periodic vibration of 1ift which is induced by wake vortexes due to f1ow separation. The f1uid f1ow near boundary 1ayer is changed and the f1ow separation is suppressed by the Lorentz force on the surface of cy1inder so that the f1ow fie1d tends to symmetry and the periodic vibration of 1ift is sup-pressed.The cy1inder osci11ation can be suppressed and even e1iminated for a 1arge va1ue of Lorentz force.

ordnance science and techno1ogy；f1ow contro1；vortex-induced vibration；Lorentz force；osci11atory suppression

O361

A

1000-1093（2016）05-0859-07

10.3969/j.issn.1000-1093.2016.05.012

2015-07-16

国家自然科学基金项目（11202102）；高等学校全国优秀博士学位论文作者专项资金项目（201461）

张辉（1981—），教授，博士生导师。F-mai1：zhanghui1902@126.com