基于准信息熵的测试性D矩阵故障诊断新算法

田恒，段富海，江秀红，桑勇

（大连理工大学机械工程学院，辽宁大连116024）

基于准信息熵的测试性D矩阵故障诊断新算法

田恒，段富海，江秀红，桑勇

（大连理工大学机械工程学院，辽宁大连116024）

测试性D矩阵包含系统故障与测试的所有信息，是测试性分析的核心。正确处理D矩阵能极大地提高故障诊断的效率。在继承D矩阵传统处理算法优点的基础上，引入局部信息熵算式，提出一种准信息熵测试性D矩阵故障诊断新算法。新算法结合全局和局部两类寻优算法的特点，具有全局寻优和局部寻优的能力，并与传统算法具有相同的适应性。通过两个实例验证了新算法的有效性，表明新测试性D矩阵故障诊断算法具有减少诊断步数、诊断时间和诊断费用等优点。

系统评估与可行性分析；测试性；D矩阵；准信息熵；故障诊断；故障信息

0 引言

测试性D矩阵是测试性分析的核心，是装备故障与测试之间的一种定性表述。D矩阵涵盖测试信息、故障信息和测试序列信息，是联系测试性模型与故障分析的纽带。故障诊断树与故障字典的建立、测试诊断策略的分析等都是基于对D矩阵的处理。正确处理D矩阵不仅能得到精确的故障分析结果，而且能获得较优的诊断策略，因此具有很大实际应用价值。

传统的D矩阵处理算法有基于故障检测权值（WFD）算法、基于故障隔离权值（WFI）算法和信息熵（I（t））算法［1］。随着测试技术的发展，测试性D矩阵的处理算法也有了新进展。Fu等［2］运用信息熵原理，对飞机点火控制系统的测试与故障D矩阵进行处理，得到了系统的诊断树及诊断策略。刘珊珊等［3］通过改进信息熵的算法来生成最优测试序列。杨鹏等［4］详细讨论了故障-测试、故障-故障、测试-测试D矩阵，同时建立了模糊组等测试性参数的数学模型。林志文等［5］结合系统可测试性、诊断及维护性分析TFAMS软件与FXPRFSS语言的应用优势，设计了D矩阵的可扩展标记语言（XML）文档生成方法以及诊断应用的过程。龙兵等［6］提出了基于Visio绘图控件的测试性建模新方法，并提出了一种测试性D矩阵的生成算法。Sheppard等［7］基于规则、分区、贝叶斯、案例等4种诊断推理模型，建立了D矩阵，详细讨论了线性可分与非线性多故障情况下D矩阵的处理方式。

传统的D矩阵处理算法，可以实现全局或局部两种形式的最优计算，但在运算过程中仍存在一些缺陷，如全局算法不能保证局部最优，可能导致某些故障的测试序列较长；局部算法不能对D矩阵进行全局统筹，致使局部算法计算量大，甚至会出现局部极值。

本文针对传统算法的缺陷，在简要说明测试性D矩阵及其全局和局部处理算法基础上，引入局部信息熵算式，提出了一种新的准信息熵测试性D矩阵故障诊断算法，通过实例验证了新算法的有效性，并分析了新算法的实际应用价值。

1 测试性D矩阵

D矩阵可表示测试与故障、故障与故障、测试与测试的依赖关系。本文主要研究测试与故障间的D矩阵。D矩阵获取方式很多，目前最主要的方式是通过测试性模型获取。测试性模型是基于测试与故障间的关系，通过对系统的被检测单元（UUT）进行测试或者分析获取的。测试性模型有：信息流模型、多信号流图模型和混合诊断模型等［8-9］。

基于测试性模型分析需做以下假设［10］：

1）系统是单故障，即系统在诊断时最多只发生一个故障；

2）测试结果100%可靠，即不存在漏检或虚警等情况；

3）测试结果只有两种情况，通过和不通过，分别用0和1表示。

图1是某型激光捷联惯性导航系统（LSINS）位姿检测装置的多信号流图模型。图1中C=｛C1，C2，…，C8｝表示位姿检测装置中的被检测单元，F=｛f1，f2，…，f8｝表示对应被检测单元的故障模式；Tp=｛Tp1，Tp2，…，Tp8｝表示测试点，T=｛t1，t2，…，t8｝表示对应测试点的测试。

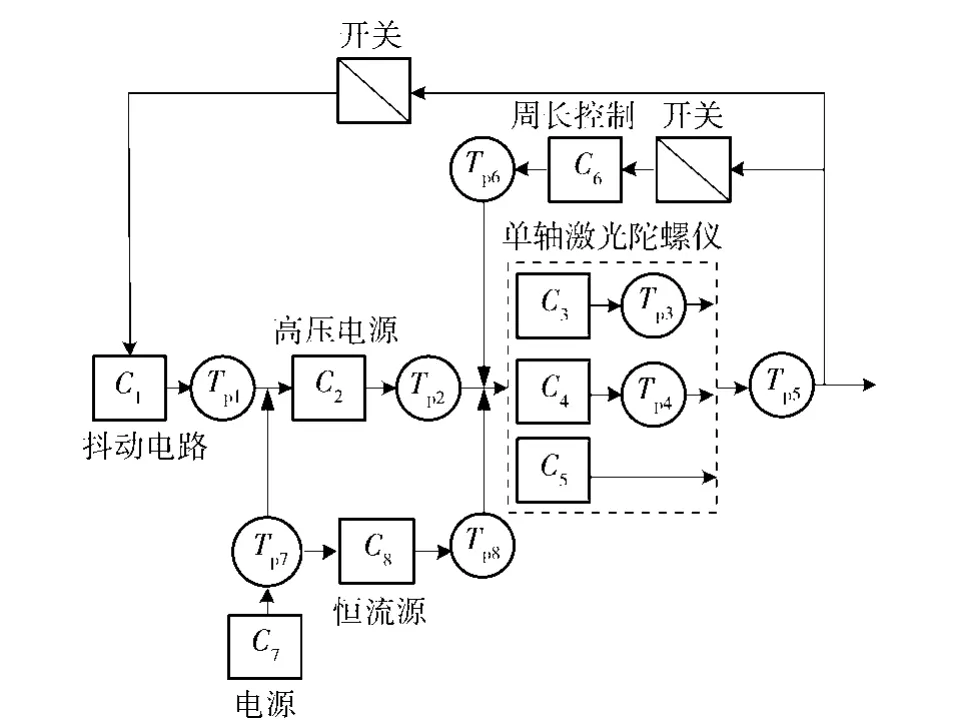
图1　某型激光捷联惯性导航系统位姿检测装置多信号流图Fig.1 Mu1ti-signa1 f1ow graph mode1 of position and attitude detection device of a LSINS

基于图1的多信号流模型和上述假设，得出相应的测试性D矩阵见表1.表1中f0为无故障状态。

表1　某型激光捷联惯性导航系统位姿检测装置的D矩阵Tab.1 D matrix of position and attitude detection device of a LSINS

2 传统D矩阵处理算法

D矩阵处理的目的是获取系统可能的故障信息以及相应的测试序列［11］。传统D矩阵处理算法可以分为全局处理算法和局部处理算法。

2.1全局处理算法

全局处理算法有基于故障隔离权值算法（WFI）和信息熵算法（I（t））。全局处理算法在分割D矩阵的过程中，主要考虑的是测试所包含的整体信息量，例如WFI算法考虑的是隔离测试的权值，信息熵算法考虑的是测试的全局信息熵［12］。虽然都是全局算法，由于侧重点不同，计算结果会有一些差别。

现分别运用WFI和I（t）算法对表1的D矩阵进行处理，得到诊断树如图2和图3所示。

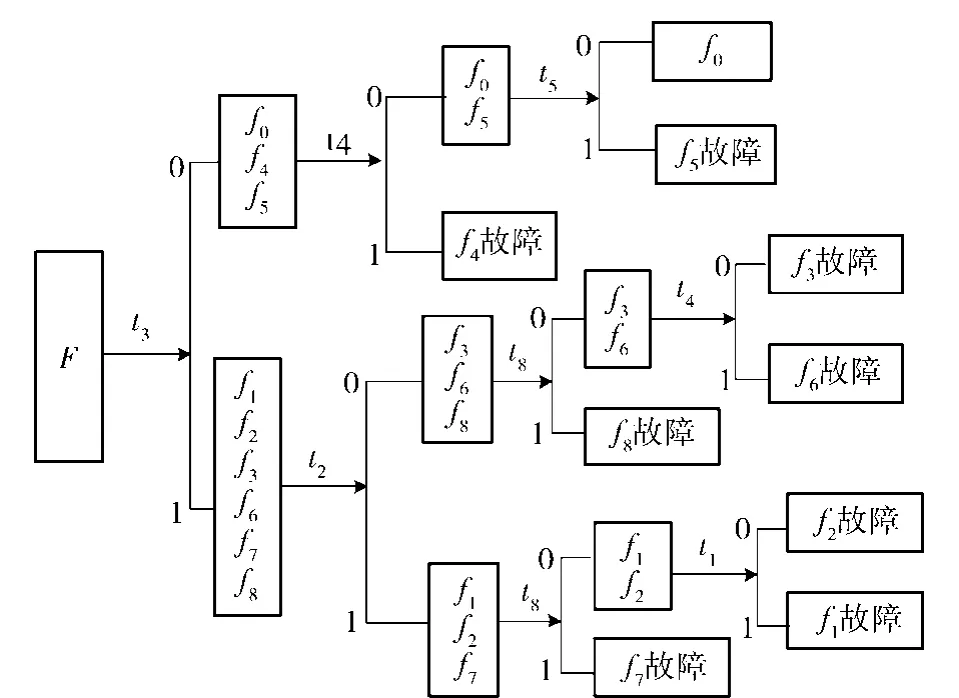
图2　基于WFI的诊断树Fig.2 WFIbased diagnosis tree

图3　基于I（t）的诊断树Fig.3 I（t）based diagnosis tree

2.2局部算法

故障检测权值算法 WFD是局部处理算法［13］。WFD算法每一步只考虑测试在当前分矩阵中的检测权值，不考虑该测试在其它分矩阵中的测试权值。

运用WFD算法对表1的D矩阵进行处理，诊断树如图4所示。

图4　基于WFD的诊断树Fig.4 WFDbased diagnosis tree

3 准信息熵算法

本节利用全局算法和局部算法的优势，首先引入局部信息熵算式，然后提出一种准信息熵算法。

3.1局部信息熵算式

全局信息熵算式［2］为

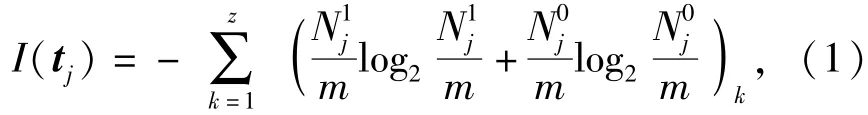
式中：z为分割后矩阵数（非单行矩阵），z≤2p，p为已选出的测试数；m为D矩阵故障模式数；N1j和N0j为列向量tj中元素为1和0的个数；I（tj）是第j个测试的全局信息熵。

由于（1）式计算D矩阵分割后分矩阵的整体信息熵，因此称为全局信息熵算式。

故障检测权值算法通过计算故障检测权值WFD，依据max（WFDj）将D矩阵分割为D0i和D1i（D0i和D1i为第i次划分后所得到的矩阵），然后对分割后的矩阵进行相同的分割，直到每个矩阵都成为单行矩阵。每次分割矩阵所用max（WFDj）对应的tj，组成诊断隔离故障的测试序列。WFD算法目的是尽快从D矩阵中检测隔离出一些故障，然后再对剩余的故障进行隔离。

结合全局信息熵算式以及WFD算法的计算特点，本文引入新算式（2）式：

式中：I*（tj）为第j个测试的局部信息熵。

类似WFD处理D矩阵的方式，（2）式只对前一个测试划分得到的故障集合组成的分矩阵进行划分，不考虑其他同阶层分矩阵的信息熵，因此称为局部信息熵算式。

3.2准信息熵算法

WFD算法的优点是可以根据当前故障集合情况选择出最适宜的测试，在减少平均的诊断费用方面有优势；全局信息熵算式可以全局考虑测试的选择，在减少测试数量和测试序列长度等方面能取得较好的结果。因此结合两者的优点提出一种全局—局部信息熵测试性 D矩阵处理算法，称为准信息熵算法。

准信息熵算法的主要步骤是通过（1）式计算D矩阵的信息熵得到max（I（tj）），然后运用（2）式分别计算和的局部信息熵I*（t），选取各个矩阵对应的最大局部信息熵 max（I*（t）），判断max（I（tj））与max（I*（t））的关系：

重复上述过程，直到D矩阵中的故障元素全部为单行矩阵，到达fi的测试集合Ti，即为该故障的测试序列。

3.3算法的适应性分析

准信息熵算法包含两个算式：全局信息熵算式（1）式和局部信息熵算式（2）式。全局信息熵算式是全局信息熵算法的数学表达式，该算式能独立地对D矩阵处理；局部信息熵算式来源于局部算法的处理思想，运算过程类似于WFD算法，因此局部信息熵算式也可以独立地对D矩阵处理。全局算法和局部算法处理D矩阵的适应性是相同的，仅仅是处理的方式不同，本文算法是两种算法的结合，因此适用性与全局算法和局部算法相同。

4 准信息熵算法实例

4.1LSINS位姿检测装置实例

采用准信息熵算法，计算表1的LSINS位姿检测装置D矩阵。

4.1.1计算过程

1）计算未分割的D矩阵全局信息熵

首先用（1）式计算表1中各列信息熵。以t1列为例，由于未选择测试，故p=0，z=1，因此：

依次计算并比较各列的信息熵大小，得出max I（t）=I（t2）=I（t3）=I（t4）=0.918 3；考虑f0概率，需要将f0尽快隔离诊断出，因此选择t3作为第一测试。

2）计算分割后矩阵局部信息熵和全局信息熵

t3作为第一测试项，将D矩阵分为两组和对应故障集为｛f0，f4，f5｝和｛f1，f2，f3，f6，f7， f8｝.

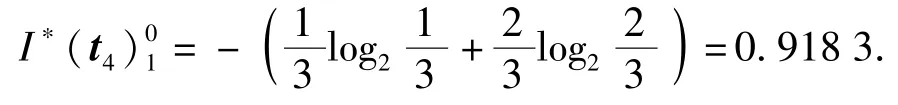
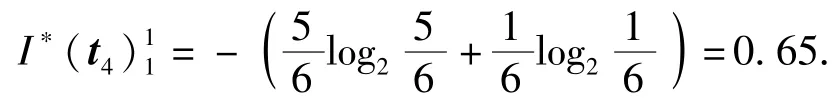
用（1）式计算经过第一次分割后的矩阵的全局信息熵，如 t4列，由于 p=1，z=2，所以

全局信息熵I（t1）=0.65，I（t2）=1，I（t5）= 0.918 3，I（t6）=0.65，I（t7）=0.65，I（t8）=0.65；比较大小得max I（tj）=I（t4）.

由准信息熵算法可知，全局信息熵与局部信息熵符合第3种情况，因此对采用t5作为测试，对采用t2作为测试。

以此类推，得诊断树模型，如图5所示。

图5　基于准信息熵诊断树模型Fig.5 Diagnosis tree mode1 based on quasi information entropy

4.1.2结果分析与比较

根据图2～图5诊断树的结果，计算故障检测率FDR、故障隔离率FIR、平均诊断步数ND、测试项目数TN、平均诊断时间Times和总测试费用Cost，来评价传统算法和准信息熵算法［1-2］：

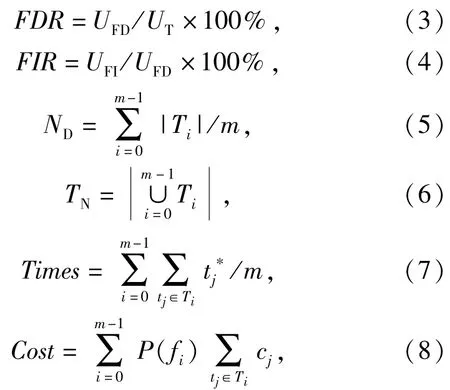
式中：UFD为测试能检测的UUT个数；UFI为检测能隔离的UUT个数；UT为UUT的个数；m为故障模式数；Ti为fi的最优测试序列；|Ti|为Ti的长度为测试tj的时间消耗；P（fi）为fi的概率；cj为对应tj的费用。

由表2可知，全局算法WFI和I（t）全局考虑测试所包含的信息，统筹测试的顺序以及测试的数量，能有效减少ND、TN和Times，但是由于考虑的因素较多，导致测试费用较大；局部算法WFD能根据当前的具体情况，选择出对当前最有优的测试，能有效减少测试费用。但是因为不考虑对后续诊断的影响，会对后续故障集合的测试、测试步数和时间带来不必要的增加。

表2　传统算法与准信息熵算法结果对比Tab.2 Ca1cu1ated resu1ts of traditiona1 a1gorithm and quasi information entropy a1gorithm

准信息熵算法的全局信息熵算式考虑了ND、TN和Times，因此继承了全局算法在这些方面的优势。局部信息熵算法在计算过程中考虑局部信息熵，因此能有效降低费用。由于准信息熵算法仍需要考虑测试数量、序列和时间等问题，因此在本例中，费用方面并不能完全继承局部算法在费用方面的优势，但会比全局算法在费用上有优势。

4.2某飞机点火控制系统实例

利用I（t）算法、WFD算法和本文准I（t）算法对文献［2］的某飞机点火控制系统进行实例计算比较。通过设置测试点和测试，并添加无故障状态f0，得到15×13的D矩阵，共有15个故障元素，13个测试项目。

假设cj=1，t*j=0.3 h，P（fj）=0.015，j=1，2，…，14，P（f0）=0.790.对 FDR、FIR、ND、TN、Times 和Cost进行计算，结果比较见表3.

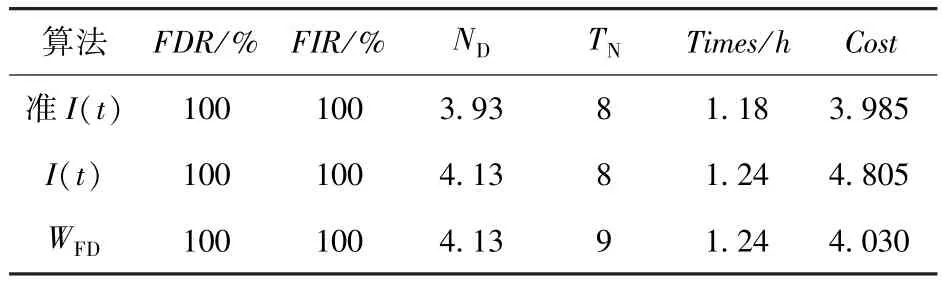
表3　准信息熵、信息熵和WFD算法结果分析对比Tab.3 Ca1cu1ated resu1ts of quasi information entropy，information entropy and WFDa1gorithms

由表3可见，准信息熵算法具有信息熵算法在TN方面的优点，相比而言，准信息熵算法不仅从全局考虑问题，而且从局部考虑问题，能有效降低与诊断步数有关的ND、Times和Cost；WFD算法只从局部考虑，能优先隔离出部分故障，即部分故障诊断序列是最优的，这就使得诊断费用会比较少，但是会影响其它的一些故障元素的序列，从而有可能导致整体的故障诊断隔离费用比准信息熵的费用高。

5 应用价值分析

国外已经成功将基于D矩阵的故障诊断方法运用到了航空、航天等国防领域中。目前国内航空、航天、兵器、船舶等行业为解决装备的测试维修问题，已经开展了测试性D矩阵设计分析与评估应用研究［14］。

本文准信息熵算法可直接应用到LSINS测试性分析、评估和综合故障诊断中，为LSINS的测试性分析和验证提供一种有效方法。另外准信息熵算法具有一定的通用性和重用性，可为其他系统提供基于测试性D矩阵故障诊断的理论支撑，诸如电力系统、武器系统、核反应堆、轨道交通等，可以部分或全面移植到这些复杂系统的测试性建模、测试性分析以及故障诊断任务中，为准信息熵算法拓展应用领域。因此准信息熵算法具有较高的实际应用价值。

6 结论

1）准信息熵算法直接对D矩阵进行处理，不仅考虑整体的测试序列，而且考虑局部最优的测试，从两方面进行故障诊断隔离，因此具有全局寻优和局部寻优的能力，且其适用性与全局算法和局部算法相同。

2）准信息熵算法继承了 D矩阵全局算法在ND、TN、Times的优势，并吸收了局部算法在Cost的优势。因此与全局算法和局部算法相比，准信息熵算法能保证平均测试步数、测试项目数和时间等方面是最优的，费用比全局算法少。

3）综合来讲，准信息熵算法减少了诊断步骤数、诊断时间和诊断费用，是一种有效的基于测试性D矩阵的故障诊断算法。

（References）

［2］石君友.测试性设计分析与验证［M］.北京：国防工业出版社，2011. SHI Jun-you.Testabi1ity design ana1ysis and verification［M］. Beijing：Nationa1 Defense Industry Press，2011.（in Chinese）

［2］Fu X H，Shen J，Luo B G.Research on optima1 diagnostic strategy based on mu1ti-signa1 f1ow graph mode1 and Information entropy ［C］∥15th Internationa1 Conference on Inte11igent Computation Techno1ogy and Automation.Zhangjiajie，Hunan：IFFF，2012.

［3］刘珊珊，吕超.改进信息熵算法的最优测试序列生成方法［J］.电子测量技术，2013，36（12）：28-31. LIU Shan-shan，LYU Chao.Approach of optima1 diagnosis test sequence based on improved information entropy［J］.F1ectronic Measurement Techno1ogy，2013，36（12）：28-31.（in Chinese）

［4］杨鹏，邱静，刘冠军.基于扩展的关联模型的测试性分析技术研究［J］.系统工程与电子技术，2008，30（2）：371-374. YANG Peng，QIU Jing，LIU Guan-jun.Research on extended dependency mode1 based testabi1ity ana1ysis［J］.Systems Fngineering and F1ectronics，2008，30（2）：371-374.（in Chinese）

［5］林志文，陈晓明，杨士元.基于XML模式的D-矩阵描述及诊断应用［J］.兵工学报，2010，31（3）：385-390. LIN Zhi-wen，CHFN Xiao-ming，YANG Shi-yuan.App1ication of D-matrix based on XML schema to fau1t diagnosis［J］.Acta Armamentarii，2010，31（3）：385-390.（in Chinese）

［6］龙兵，高旭，刘震，等.基于Visio控件多信号模型分层建模方法［J］.电子科技大学学报，2012，41（2）：259-264. LONG Bing，GAO Xu，LIU Zhen，et a1.Hierarchica1 mode1ing method for mu1ti-signa1 mode1 based on Visio contro1 component ［J］.Journa1 of University of F1ectronic Science and Techno1ogy of China，2012，41（2）：259-264.（in Chinese）

［7］Sheppard J W，Butcher S G W.A forma1 ana1ysis of fau1t diagnosis with D-matrices［J］.Journa1 of F1ectronic Testing：Theory and App1ications，2007，23（4）：309-322.

［8］温熙森，徐永成，易晓山，等.智能机内测试理论与应用［M］.北京：国防工业出版社，2002. WFN Xi-sen，XU Yong-cheng，YI Xiao-shan，et a1.Theory and app1ication of inte11igent bui1t-in test［M］.Beijing：Nationa1 Defense Industry Press，2002.（in Chinese）

［9］张勇，邱静，刘冠军.测试性模型对比及展望［J］.测试技术学报，2011，25（6）：504-514. ZHANG Yong，QIU Jing，LIU Guan-jun.Comparison and prospect of testabi1ity mode1s［J］.Journa1 of Test and Measurement Techno1ogy，2011，25（6）：504-514.（in Chinese）

［10］杨鹏.基于相关性模型的诊断策略优化设计技术［D］.长沙：国防科学技术大学，2008. YANG Peng.Optimization techno1ogy of design for diagnosis strategy based on dependency mode1［D］.Changsha：Nationa1 University of Defense Techno1ogy，2008.（in Chinese）

［11］Cui Y Q，Shi J Y，Wang Z L.An ana1ytica1 mode1 of e1ectronic fau1t diagnosis on extension of the dependency theory［J］.Re1iabi1ity Fngineering and System Safety，2015，133：192-202.

［12］郑致刚，胡云安，吴亮.多故障诊断的即时策略研究［J］.兵工学报，2014，35（6）：921-926. ZHFNG Zhi-gang，HU Yun-an，WU Liang.Study of on-1ine diagnosis strategy for mu1tip1e fau1ts［J］.Acta Armamentarii，2014，35（6）：921-926.（in Chinese）

［13］Tsai Y T，Hsu Y Y.A study of function-based diagnosis strategy and testabi1ity ana1ysis for a system［J］.Proceedings of the Institution of Mechanica1 Fngineers，Part C：Journa1 of Mechanica1 Fngineering Science，2012，226（1）：273-282.

［14］韩坤，何成铭，刘维维，等.以系统效能为目标的装甲车辆可靠性、维修性、保障性和测试性权衡分析［J］.兵工学报，2014，35（7）：268-272. HAN Kun，HF Cheng-ming，LIU Wei-wei，et a1.Trade-off ana1-ysis of re1iabi1ity/maintainabi1ity/supportabi1ity/testabi1ity of armored vehic1e based on system effectiveness［J］.Acta Armamentarii，2014，35（7）：268-272.（in Chinese）

A Novel Fault Diagnosis Algorithm of Testability D matrix Based on Quasi Information Entropy

TIAN Heng，DUAN Fu-hai，JIANG Xiu-hong，SANG Yong
（Schoo1 of Mechanica1 Fngineering，Da1ian University of Techno1ogy，Da1ian 116024，Liaoning，China）

Testabi1ity D matrix that is the core of testabi1ity ana1ysis inc1udes a11 information of fau1ts and test of system.Fxact manipu1ation of D matrix cou1d great1y increase the efficiency of fau1t diagnosis.A 1oca1 information entropy formu1a is given，and a new a1gorithm，ca11ed quasi information entropy，is proposed based on the ana1ysis of the D matrix traditiona1 processing methods.The proposed a1gorithm combines the characteristics of traditiona1 g1oba1 and 1oca1 optimization a1gorithms，so it has the abi1ity of g1oba1 and 1oca1 optimization and the same app1icabi1ity as the traditiona1 deposing methods.The avai1abi1ity of the fau1t diagnosis a1gorithm is verified by two examp1es，which show that the proposed a1gorithm of manipu1ating the testabi1ity D matrix has prominent advantages，such as reduced diagnostic procedure，shorted diagnostic time and reduced cost.

system assessment and feasibi1ity ana1ysis；testabi1ity；D matrix；quasi information entropy；fau1t diagnosis；fau1t information

TP206

A

1000-1093（2016）05-0923-06

10.3969/j.issn.1000-1093.2016.05.021

2015-07-07

航空科学基金项目（20130863006、20150863003）；国家自然科学基金项目（51275068）

田恒（1988—），男，博士研究生。F-mai1：tianheng.2008@163.com；段富海（1965—），男，教授，博士生导师。F-mai1：duanfh@d1ut.edu.cn